Vettori
Vettori
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Vettori
PARTE 1: aspetti introduttivi
1. DEFINIZIONE: sono grandezze vettoriali tutte quelle grandezze misurabili che vengono descritte da un numero di informazioni >1 (le informazioni citate sono le cosiddette dimensioni).
Esse dunque si differenziano dalle altre grandezze gestite dalla fisica e chiamate scalari che invece, per essere completamente note, necessitano di un solo dato (cioè numero e unità di misura).
2. CARATTERISTICHE DI UN VETTORE: in fisica si studiano grandezze del mondo reale (che è un mondo tridimensionale) per cui, nei problemi da noi considerati, i vettori sono caratterizzati da tre informazioni. Quali sono? Sono quelle che permettono di individuare chiaramente il vettore nello spazio (direzione, verso e intensità – o modulo).
3. RAPPRESENTAZIONE DI UN VETTORE: viene utilizzato il simbolo (geometrico) della freccia per il semplice motivo che tale simbolo permette, con un unico oggetto, di descrivere tutte e tre le caratterisitche del vettore prima citate. Altra convenzione di rappresentazione vettoriale è quella di utilizzare lettere in grassetto o con una piccola freccia rappresentata sulla lettera medesima.

4. GRANDEZZE FISICHE VETTORIALI: sono molteplici, anche se la più importante è sicuramente la forza.
5. OSSERVAZIONI: le problematiche inerenti alla gestione delle grandezze vettoriali sono esclusivamente legate al fatto che esistono operazioni “matematiche” particolari per essi: la cosiddetta algebra vettoriale. Essa sarà argomento di questa dispensa.
PARTE 2: la rappresentazione grafica dei vettori
Dovendo gestire oggetti geometrici, risulta necessario utilizzare strumenti geometrici di rappresentazione. Nel nostro caso noi utilizziamo il sistema di riferimento cartesiano quale elemento convenzionale di rappresentazione dei vettori.
Ricordiamo che tale strumento consiste in due rette orientate perpendicolari tra loro e associate, attraverso la scelta di opportuna scala, all’insieme dei numeri reali (le rette sono due per i problemi nel piano e tre per i problemi nello spazio).
Così come la scala scelta per gli assi permette la rappresentazione dei moduli dei vettori, così il grado sessagesimale permette la gestione delle direzioni dei vettori.Spieghiamoci meglio attraverso un esempio concreto. Si debba rappresentare in un sistema di riferimento cartesiano il vettore F1 così descritto (detta forma polare, ovvero modulo e angolo):
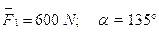
Si opera attraverso i seguenti punti:
- si rappresenta il SR cartesiano (y verticale, ordinata, e x orizzontale, ascissa);
- si sceglie la scala di lettura del grafico in funzione del valore numerico da gestire (in questo caso scegliamo un’unità pari a 100 N) e la si indica vicino al grafico;
- si individuano direzione e verso del vettore (entrambe le informazioni sono legate all’angolo dato) secondo la convenzione relativa agli angoli: l’angolo si misura a partire dal semiasse positivo delle ascisse ruotando in senso antiorario per descrivere un angolo positivo, oppure in senso orario per descrivere un angolo negativo; per un disegno corretto risulta indispensabile l’utilizzo del goniometro.
- Se non è diversamente specificato i vettori, per comodità, si fanno partire dall’origine degli assi (il punto di inizio del vettore è definito punto di applicazione).

OSSERVAZIONI - E’ facile notare che:
- lo stesso vettore si otterebbe se, invece dell’angolo di +135° , fosse stato dato come valore angolare l’angolo β = -225° (ovvero l’angolo esplementare 360°- α );
- il SR cartesiano è tale per cui il piano si divida convenzionalmente nei cosiddetti quattro quadranti (I, II, III e IV) in cui le coordinate x e y sono, rispettivamente, (+;+); (-;+); (-;-) e (+;-) laddove si ricordi che il primo segno nella parentesi indica l’ascissa e il secondo l’ordinata;
- i vettori opposti si differenziano per angoli piatti (cioè di 180°); nel nostro esempio rappresentiamo il vettore opposto F2 = - F1: (NB: indicare quella scrittura o la seguente F1 = - F2è del tutto equivalente)

PARTE 3: forma polare e cartersiana di un vettore
Abbiamo sottolineato nella parte precedente che descrivere un vettore attraverso il valore del modulo e un angolo significa gestire la cosiddetta forma polare del vettore. E’ però possibile utilizzare un’altra forma di rappresentazione (detta cartesiana) di un vettore. Vediamo in cosa consista utilizzando lo stesso vettore di esempio F1.
Innanzitutto: Scomporre un vettore significa trovare altri due (nel piano) o tre (nello spazio) vettori, la cui somma sia uguale al vettore dato. Se si scelgono come direzioni di scomposizione di un vettore v gli assi cartesiani x e y, allora le componenti del vettore sono dette componenti cartesiane. I moduli di tali componenti sono detti rispettivamente componente x e componente y e vengono di solito indicate con vx e vy. Come fare a rappresentare tali componenti? E’ sufficiente semplicemente tracciare dei segmenti paralleli ai due assi del SR e uscenti dalla punta del vettore; si individuano così sugli assi due nuovi vettori che sono le rispettive componenti cercate. Nel nostro caso:

Quanto valgono? Grazie alla scala del grafico è possibile determinare approssimativamente che esse valgono circa 4 unità, ovvero 400 N (ATTENZIONE: in questo caso la componente x vale in realtà -400N nel nostro SR perché ha verso opposto a quello del semiasse x positivo). Vedremo inoltre tra breve come il gestire la matematica adeguata ci permetterà di evitare anche queste imprecisioni grafiche. Ma che significato hanno le componenti? Quello di permettere a chi studia i vettori di “trasferire” qualsiasi vettore sui due assi del SR. Infatti si può vedere facilmente come la regola del parallelogramma applicata alle due componenti mi faccia ottenere il vettore di partenza. In altri termini la somma vettoriale delle due componenti equivale al vettore dato! Dunque gestire il vettore iniziale o le sue due componenti è, alla fine dei nostri scopi, indifferente. Si scrive che:

In cui il simbolo “+” indica in realtà la somma vettoriale (regola del parallelogramma). La precedente è appunto la cosiddetta forma cartesiana del vettore. Quella che apparentemente sembra una complicazione (passare da un oggetto unico a due equivalenti) vedremo invece che offre notevoli facilitazioni di calcolo per certe operazioni vettoriali.
OSSERVAZIONE 1: come si passa dalla forma cartesiana a quella polare o viceversa? Per rispondere a questa domanda è necessario inizialmente fare una premessa. Noi utilizzaremo delle funzioni matematiche il cui significato vedrete nel prosieguo degli studi e che non è necessario conoscere per i nostri scopi. Nelle calcolatrici scientifiche sono indicate con i seguenti tasti:

Per attivare le funzioni seno, coseno tangente si digita il tasto nero, per attivare le funzioni inverse (quelle scritte in alto sopra ciascun tasto nero) si deve digitare il medesimo tasto ma dopo aver attivato il tasto “second” (o “shift”, o “2nd”) presente in ogni calcolatrice con colore differente dagli altri. Cosa fanno queste funzioni?
SENO, COSENO e TANGENTE à agiscono su angoli à danno come risultato un numero
SENO-1, COSENO-1 e TANGENTE-1à agiscono su numeri à danno come risultato un angolo
Per essere più precisi per quanto riguarda le funzioni dirette qualunque valore di angolo voi inseriate (per noi sono valori compresi tra 0° e 360°) otterrete:
- per seno e coseno un risultato numerico compreso tra -1 e +1;
- per la tangente un valore qualsiasi;
Per le funzioni inverse invece:
- qualunque valore numerico tra -1 e +1 voi inseriate con seno e coseno otterrete un angolo compreso tra 0° e 360° se invece inserite valori esterni a tale intervallo la calcolatrice segnalerà un errore;
- qualunque valore numerico voi inseriate utilizzando la tangente voi otterrete un angolo compreso tra 0° e 360°
Provate, come esercizio, a verificarte la corretta veridicità della seguente tabella con la vostra calcolatrice (verificando che sul visore compaia, in piccolo, il simbolo “DEG” che significa che la calcolatrice legge come angoli in gradi i valori che voi digitate).

Ebbene, fatta questa premessa, diamo una risposta alla domanda iniziale.
Forma polare à Forma cartesiana
E’ sufficiente moltiplicare il vettore dato per il coseno (per ottenere la componente su x) oppure per il seno (per ottenere la componente su y): Dunque, nell’esempio:

Forma cartesianaà Forma Polare
Per trovare il modulo del vettore è sufficiente applicare Pitagora al valore delle due componenti (il segno positivo o negativo delle medesime non incide sul risultato finale):
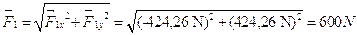
Più complicata la determinazione dell’angolo. Lo si determina in due fasi:
- nella prima si effettua il calcolo della funzione inversa della tangente del rapporto tra la componente y e quella x prendendone solo i loro valori (cioè con segno sempre positivo); nel nostro caso chiamiamo π l’angolo così determinato:

- a seconda del quadrante in cui ci si trova si determina poi l’angolo α del vettore attraverso queste operazioni:
QUADRANTE |
ANGOLO del VETTORE |
Primo |
π |
Secondo |
180° - π |
Terzo |
π + 180° |
Quarto |
360° - π |
PARTE 4: l’algebra vettoriale
Quali sono le operazioni che si possono effettuare nel mondo dei vettori? Le elenchiamo in questo schema:
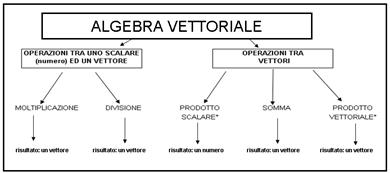
In questa dispensa noi consideriamo soltanto quelle più semplici (quelle asteriscate verranno trattate al triennio).
- moltiplicazione di un vettore per un numero: l’operazione non comporta la variazione della direzione del vettore; è sufficiente ricordare di moltiplicare il valore del modulo per il numero dato con l’avvertenza di cambiare il verso del vettore se il numero dato è negativo. Ricordarsi inoltre che quello che così facendo si trova è un nuovo vettore, inoltre ricordarsi che tale operazione è più semplice se si considera il vettore dato inizialmente nella forma polare.(NB: il modulo, alla fine NON è mai negativo, il segno negativo del numero influisce solo sull’angolo!). Di seguito alcuni esempi

- divisione di un vettore per un numero: considerazioni del tutto analoghe al punto precedente; si deve però effettuare la divisione e non la moltiplicazione. Dati gli stessi esempi si trova:

- somma di vettori: questa operazione, a differenza delle precedenti, è semplice nel momento in cui i vettori siano espressi in forma cartesiana. Vediamola in dettaglio attraverso un esercizio di esempio. Tra l’altro, con questa operazione, si intuisce perché sia così comodo l’utilizzo delle componenti infatti, mentre la regola del parallelogramma si può applicare a due soli vettori per volta, questa operazione si può applicare a quanti vettori si voglia contemporaneamente. Infine, mentre la regola del parallelogramma è molto imprecisa in quanto strumento grafico, questa operazione invece è matematicamente corretta. Di seguito l’esempio per esteso. NB: quando si parla di “somma” si intende in realtà la “somma algebrica” ovvero qualsiasi operazione che abbia i segni + e – (infatti la sottrazione non è altro che la somma di un opposto). Nell’esempio chiariremo questo aspetto.
ESEMPIO DI SOMMA
Dati i seguenti tre vettori in forma polare, effettuare l’operazione indicata ed esprimere il risultato finale nuovamente in forma polare.
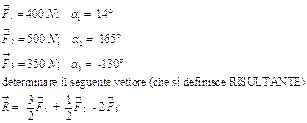
SOLUZIONE
Premessa. Analizziamo la richiesta del testo. L’operazione richiesta è una “somma algebrica” di tre elementi vettoriali.
Il primo vettore è i 3/2 di F1 ; il secondo vettore è la metà di F2 mentre il terzo è il doppio dell’opposto di F3.
Operiamo attraverso questi punti:
- rappresentiamo i tre vettori dati in un SR cartesiano dopo aver scelto la scala opportuna per questo esempio; gli angoli si misurano attraverso il goniometro (NB: però, risolvendo con questo sistema, non è più necessario essere assolutamente precisi relativamente al grafico in quanto lavoreremo solo con la matematica). Anche per questi numeri è comoda l’unità 100 N.

2 . prima di poter effettuare la somma algebrica dobbiamo ricavare i tre nuovi vettori sfruttando il fatto che essi sono in forma polare per cui è semplice moltiplicarli per un numero come indicato nell’operazione e applicando quanto visto per quello che riguarda l’operazione di moltiplicazione di un vettore per un numero:

3. a questo punto rappresentiamo i nuovi tre vettori nel nostro sistema cartesiano (per evitare confusione è meglio riprodurne uno uguale).

NB: avendo determinato questi tre nuovi vettori attenzione che adesso calcolare la risultante significa semplicemente calcolare:

4. Ci siamo quindi portati alla situazione di dover effettuare una somma algebrica di vettori; come detto necessitiamo quindi di avere la forma cartesiana dei vettori (il perché lo vedremo a breve). Applicando quanto precedentemente visto nella parte relativa, determiniamo le tre forme cartesiane:

Questi calcoli evidenziano anche analiticamente quello riscontrabiòe dal punto di vista grafico; infatti, rappresentando come spiegato le varie componenti troviamo sul SR che:

Dal grafico si nota come vi sia solo la componente x del secondo vettore che risulta con verso opposto agli assi convenzionali (infatti è caratterizzata da un valore negativo).
5. Adesso possiamo facilmente determinare la risultante; infatti, essendo anch’essa un vettore, sarà scrivibile attraverso le sue due componenti, ovvero vale la seguente relazione:

E come fare a determinare le due componenti? Semplicemente sommando i valori delle corrispondenti componenti trovate nel punto precedente (nel nostro esempio sono tre, ma potrebbero essere un numero qualsiasi); in altri termini possiamo scrivere che:

6. Trasformiamo infine la precedente forma cartesiana in quella polare come richiesto; determiniamo dunque per primo il modulo della risultante:

Siccome siamo nel primo quadrante (entrambi le componenti positive) il calcolo dell’angolo è semplicemente la relazione inversa della tangente come visto in precedenza:

E di conseguenza rappresentiamo il risultato sul nostro SR cartesiano:

Fonte: http://www.sobrero.it/Studenti/materiali%20fisica%2011_12/DISPENSA%20DI%20FISICA%20-%20i%20vettori.doc
Autore del testo: non indicato nel documento di origine
Parola chiave google : dispensa di fisica tipo file : doc
Visita la nostra pagina principale
Vettori
Termini d' uso e privacy