Astronomia appunti parte 2

 

 

 

Astronomia appunti parte 2

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

Le unità di misura fotometriche

L'unità fotometrica fondamentale (sia nel sistema SI che nel cgs) è la candela (cd), che misura l'intensità I di una sorgente luminosa. Essa viene naturalmente definita in funzione di un campione luminoso, convenzionalmente individuato.
Secondo la vecchia definizione 1 candela è pari ad 1/60 dell'intensità luminosa prodotta da 1 cm2 di corpo nero a 2042°K (temperatura di fusione del platino) entro l'angolo solido unitario (1 steradiante = 1 radiante2). Nel 1979 la XVI Conferenza Generale dei Pesi e delle Misure definì la candela come l’intensità luminosa di una sorgente di potenza 1/683 W/sr che emette una radiazione monocromatica di 5,40 1014 Hz (l = 555,016 nm)

Un steradiante è l'angolo solido sotto il quale un osservatore posto al centro di una superficie sferica  vede  una  calotta sferica di superficie R2. Essendo l'intera superficie sferica pari a 4R2, l'intero angolo solido sarà pari a 4 steradianti.
Si definisce flusso luminoso il prodotto dell'intensità luminosa per l'angolo solido attraverso cui la luce diffonde. La sua unità di misura è la candela . steradiante (cd.sr) o lumen (lm).

 

Una sorgente luminosa puntiforme di 1 candela che diffonda luce in tutte le direzioni (sull'intero angolo solido) produce un flusso luminoso di 4 lumen.
Per misurare gli effetti della luce che colpisce una superficie S si definisce l'illuminamento E, come il flusso che colpisce l'unità di superficie S, disposta perpendicolarmente ai raggi luminosi. La sua unità di misura è il lumen/m2 (o lux (lx), nel sistema SI) o lumen/cm2 (nel sistema cgs). Nel caso il flusso formi un angolo con la direzione normale alla superficie, il suo valore va moltiplicato per cos.

Non tutte le stelle presentano una luminosità costante. Le variazioni di luminosità possono essere periodiche o del tutto irregolari. Registrando il segnale luminoso in funzione del tempo si ottiene la cosiddetta curva di luce, che presenta caratteristiche diverse a seconda del tipo di variabile.
Le stelle variabili vengono indicate attraverso la seguente convenzione:
la prima variabile scoperta in una costellazione viene indicata con la lettera 'R' seguita dal genitivo del nome della costellazione. La seconda variabile scoperta in ordine di tempo viene indicata con la lettera 'S', la terza con la 'T' e così via fino alla 'Z'. Nel caso si debba andare oltre la Z si prosegue con RR, RS, RT, RU......RZ e quindi SS, ST, SU......SZ fino a ZZ.
A questo punto si continua con AA, AB, AC...AZ e poi BB, BC, BD,......BZ, fino a QZ, che indica la 334a variabile di una costellazione in ordine di scoperta. Le successive vengono indicate con V335, V336 etc.

Le stelle variabili possono essere classificate in  variabili intrinseche e variabili binarie.

A) Le variabili intrinseche o pulsanti sono stelle instabili che variano la loro luminosità a causa di modificazioni della loro temperatura e del loro volume. Esse subiscono delle espansioni e delle contrazioni, da cui il termine 'pulsanti', che determinano delle variazioni della temperatura superficiale ed una conseguente modificazione della luminosità.

All'inizio del nostro secolo A. Eddington ipotizzò che le stelle variabili funzionassero come una specie di pentola a pressione, con un meccanismo a valvola posto in superficie che aprendosi e chiudendosi periodicamente regolava il flusso di energia verso l'esterno. In tal modo si susseguivano periodi di surriscaldamento ed espansione superficiale a periodi di raffreddamento e contrazione. Eddington intuì che il grado di ionizzazione del plasma superficiale poteva fungere da valvola, ma non poté trovare conferme a tale ipotesi. Oggi si ritiene che la principale causa di pulsazione sia collegata al comportamento dell'Elio. L'Elio ionizzato una volta può infatti innescare la pulsazione quando perde anche il secondo ed ultimo elettrone. Il modello, confermato da simulazioni al computer, prevede che la contrazione della stella porti a ionizzare completamente l'Elio che diventa in tal modo opaco alla radiazione (valvola chiusa). Il calore che in tal modo si accumula produce un'espansione ed un raffreddamento dell'elio che, riacquistando l'elettrone precedentemente perso, ridiventa trasparente alla radiazione (valvola aperta).

Nel 1596 l'olandese David Fabricius individuò nella costellazione della Balena la prima variabile pulsante. Poiché a quel tempo si riteneva che le stelle fossero costituite di un'essenza incorruttibile (etere o quintessenza), lo stupore che destò la scoperta fu tale da meritarle il nome di Meravigliosa della Balena o Mira Ceti.
Oggi noi conosciamo parecchie variabili simili a Mira Ceti che vengono classificate come variabili di tipo "Mira". Si tratta di giganti rosse con periodi di variabilità che vanno dai 100 giorni ai 2-3 anni.

Le Cefeidi rappresentano un'altra classe di variabili pulsanti che prende il nome dalla prima stella scoperta con tali caratteristiche, Delta Cèphei. Le cefeidi sono giganti bianco-azzurre. Esistono in realtà più tipi di cefeidi, le principali sono: le cefeidi classiche (simili a Delta Cèphei) con periodi di variabilità che vanno da 1 a 50 giorni e le Cefeidi tipo RR Lyrae con periodi di variabilità inferiori al giorno. le Cefeidi tipo W Virginis, con periodi simili alle classiche ma mediamente meno luminose (circa 2 gradi di magnitudine).
Le Cefeidi hanno svolto un ruolo fondamentale in astronomia poiché furono tra i primi indicatori di distanza individuati. Nel 1912 Henrietta Leavitt scoprì che le Cefeidi appartenenti alla piccola Nube di Magellano, una piccola galassia satellite che si trova appena fuori della nostra galassia, presentavano una luminosità media intrinseca, proporzionale al loro periodo di variazione. In altre parole cefeidi con periodi di variabilità più lunghi si rivelavano mediamente più luminose.
Costruendo quindi un grafico periodo/magnitudine assoluta per stelle di cui si conosca la distanza è possibile utilizzarlo poi anche per cefeidi troppo lontane per poterne calcolare la distanza con metodi trigonometrici (metodi utilizzabili solo per stelle a distanze inferiori a 300 al). Così una volta individuata una cefeide in una galassia lontana, misurato il suo periodo di variabilità è possibile risalire attraverso il diagramma della Leavitt alla sua luminosità effettiva. Avendo la luminosità effettiva e misurando con un fotometro quella apparente si può infine calcolarne la distanza.

La relazione per le Cefeidi classiche è

dove Mv è la magnitudine assoluta (media) visuale e P è il periodo di variabilità in giorni. Ad esempio sapendo che per Cephei il periodo è di 5,37 giorni se ne ricava una magnitudine assoluta media pari a

Sapendo inoltre che la magnitudine visuale apparente media (misurata con un fotometro) è mv = 4, se ne ricava un modulo di distanza m - M = 7,5, da cui

 

La relazione per le W Virginis è

mentre per le RR Lyrae la magnitudine assoluta media è praticamente indipendente dal periodo e vale 0,6.

Sia le stelle tipo Mira che le Cefeidi sono considerate stelle che stanno esaurendo il loro combustibile e non riescono più a mantenere l'equilibrio meccanico e termodinamico che caratterizza invece le stelle stabili come il sole.
Ma esistono  fasi di instabilità stellare anche all'inizio del ciclo evolutivo di una stella, prima che una stella riesca a raggiungere un proprio equilibrio interno. Ne sono un tipico esempio le cosiddette variabili eruttive o "a flare", di cui le stelle tipo T-Tauri sono un caso particolare. Si tratta di stelle che presentano una variabilità estremamente irregolare, con improvvisi guizzi di luminosità. Sono dunque stelle giovani, particolarmente numerose nelle nebulose, come quella di Orione, dove si ritiene appunto che le stelle si formino a partire dalla materia nebulare.

B) Le variabili binarie sono sistemi di stelle doppie che per la loro lontananza dalla terra e/o per la loro reciproca vicinanza (doppie strette), non è possibile vedere come stelle singole nemmeno con i più potenti telescopi.
Quando la nostra visuale (retta condotta dall'osservatore all'oggetto osservato) giace sul piano orbitale di tali sistemi doppi, si producono le condizioni necessarie affinché le due stelle si eclissino alternativamente. In tal modo quando le stelle risultano separate noi osserviamo un massimo di luminosità, mentre quando le stelle si eclissano osserviamo un minimo nella curva di luce. In genere Poiché è probabile che le due stelle non presentino la stessa luminosità, i minimi nella curva di luce hanno profondità differenti. Il minimo più profondo si ha quando la stella meno luminosa eclissa quella più luminosa, mentre il minimo meno profondo si ha quando la stella più luminosa eclissa quella meno luminosa.

Tali variabili sono dette variabili a eclisse o fotometriche.
Quando il piano dell'orbita di questi sistemi doppi è talmente inclinato rispetto alla nostra visuale da non dar luogo a fenomeni di eclisse è a volte comunque possibile evidenziarli. Ciò accade quando le due stelle orbitano l'una attorno all'altra ad una velocità talmente elevata che la radiazione che emettono subisce un effetto Doppler. Compiendo osservazioni spettroscopiche in epoche diverse si potrà perciò evidenziare uno spostamento alternativo degli spettri verso il rosso e verso il blu , a seconda che sia la stella più luminosa o quella meno luminosa che in quel momento si sta allontanando o avvicinando. In tal caso non si determina una variazione nell'intensità luminosa ma una variazione periodica nella struttura dello spettro. Tali sistemi sono conosciuti come variabili spettroscopiche.

 

Massa e dimensioni

I modelli teorici prevedono che la massa delle stelle sia compresa tra 0,08 – 120 volte la massa solare (in astronomia le masse si misurano in masse solari M). Al di sotto di tali limiti non si innescano le reazioni termonucleari, al di sopra la gravità ha il sopravvento ed il sistema è destinato a collassare.
La massa delle stelle può essere stimata per via indiretta utilizzando la relazione di Eddington, che lega la luminosità intrinseca alla massa (log L = 3,5 log M). Tale relazione è però valida solo per le stelle di sequenza principale e la costante di proporzionalità necessita di essere tarata per i diversi tipi spettrali. L’unico modo per ottenere una misura diretta delle masse stellari è studiare i sistemi doppi.
I sistemi di stelle doppie o multiple non sono un'eccezione, ne sono stati osservati ormai molte migliaia. In alcuni casi è possibile osservare le due stelle separate (stelle doppie visuali) e misurare gli spostamenti relativi delle due stelle lungo archi di traiettorie ellittiche. E' ciò che fece Herschel, arrivando per primo a dimostrare l'esistenza di stelle doppie.
I sistemi di stelle doppie sono stati studiati con particolare attenzione essendo una fonte preziosa di informazioni sulle stelle. Sappiamo così che le stelle non presentano un intervallo di masse molto ampio. I valori ottenuti dall'analisi dei sistemi doppi ci dicono che le stelle hanno in genere masse comprese tra circa 1/10 e 100 M , in buon accordo con i valori previsti dalla teoria.
Maggiore è invece l'intervallo di variabilità per i diametri stellari, i quali si possono calcolare nei sistemi doppi ad eclisse sulla base dei tempi di occultamento e delle velocità di rivoluzione. Si è scoperto così che mentre le stelle più piccole hanno dimensioni pari a circa 1/100 di quelle solari, paragonabili a quelle di un pianeta terrestre (nane bianche), quelle più grandi possono superare il sole di oltre 1000 volte (supergiganti rosse), con un’escursione di circa 5 ordini di grandezza. I diametri stellari sono stati misurati anche con metodi diversi e sono risultati in buon accordo con i dati ottenuti dai sistemi doppi ad eclisse.
In generale se di una stella si conosce la temperatura superficiale T e la luminosità intrinseca bolometrica Lb è possibile calcolare il raggio. Se infatti l'energia emessa per unità di superficie e di tempo da una stella è E = sT4, l'energia totale (luminosità bolometrica) emessa da una stella di raggio R sarà

 

Temperatura e colore: i tipi spettrali

La stessa relazione può essere naturalmente utilizzata anche per calcolare la temperatura superficiale di una stella, una volta note la luminosità intrinseca bolometrica L ed il raggio R.  Tale temperatura è detta temperatura efficace Te.

La temperatura efficace è determinabile solo nel caso del sole e di poche altre stelle di cui si è potuto misurare il raggio. In tutti gli altri casi è necessario ricorrere a metodi indiretti.
Nel caso si riesca ad individuare nello spettro di una stella la lunghezza d'onda di massima emissione è possibile utilizzare la relazione di Wien
max T = K
Più spesso si ricorre alla cosiddetta temperatura di colore Tc, correlata all'indice di colore IC = mpg - mpv.

La temperatura di colore ha il vantaggio di essere determinabile solo conoscendo i dati fotometrici apparenti (su diverse bande), senza dover ricorrere alla misurazione della distanza e del raggio della stella.

Parlando delle stelle abbiamo citato 'nane bianche', 'giganti azzurre' e 'giganti rosse'. Oltre a queste esistono anche stelle gialle, come il nostro sole, e arancioni. Il colore delle stelle è una diretta conseguenza della loro temperatura superficiale. Una volta fatta passare la luce stellare attraverso uno spettrometro è infatti possibile osservare quali sono le righe più intense. Il colore della stella dipende infatti essenzialmente dalla riga di massima emissione di energia (lmax) e questa è legata alla temperatura superficiale dalla legge di Wien.
E' così che le stelle con temperature superficiali più basse (3500°K) ci appaiono rosse, mentre quelle con temperature superficiali più elevate (30.000 - 40.000°K) ci appaiono bianco-azzurre. Naturalmente dalle stelle rosse alle stelle bianco-azzurre si passa, al crescere della temperatura, alle stelle arancioni e a quelle gialle con tutte le sfumature intermedie.
Le temperature superficiali delle stelle influenzano non solo il loro spettro continuo, ma anche lo spettro a righe in modo caratteristico. Infatti al crescere della temperatura superficiale alcuni composti, che sono presenti nelle stelle più fredde, scompaiono poiché i legami chimici che li tengono uniti vengono spezzati. Dai composti si passa così agli elementi semplici, prima allo stato neutro e poi ad uno stato sempre più ionizzato. Naturalmente tutto ciò viene fedelmente registrato attraverso le righe spettrali caratteristiche che ciascuna sostanza chimica, presente alla superficie della stella, assorbe.
Le caratteristiche spettrali delle stelle, colore, tipo di righe presenti e, di conseguenza, temperatura superficiale vengono raggruppate in 7 tipi o classi spettrali principali (classificazione di Harvard), contrassegnati con le lettere O B A F G K M, che gli astronomi anglosassoni ricordano attraverso la frase "O, Be A Fine Girl Kiss Me".
Ciascuna classe spettrale viene a sua volta suddivisa in 10 sottoclassi, indicate con un numero da 0 a 9 che segue la lettera della classe.
I tipi spettrali O e B indicano le stelle bianco azzurre molto calde, mentre il tipo M le stelle rosse relativamente fredde. Il sole è una stella G2.

La classificazione spettrale fu introdotta da E.C. Pickering dell’Harvard College Observatory, verso la fine dell’800. Inizialmente Pickering propose di classificare le stelle in funzione dell’intensità delle righe dell’idrogeno, assegnando la lettera A alle stelle con righe dell’idrogeno più intense e associando via via le successive lettere fino alla O alle stelle con righe dell’idrogeno progressivamente più tenui. Il successivo lavoro di classificazione e messa a punto eseguito dalle collaboratrici di Pickering (W.P Fleming e A.J. Cannon) portò a modificare la sequenza originaria in funzione del colore. Alcune classi si rivelarono superflue e vennero pertanto eliminate, mentre le classi O e B vennero anticipate. L’imponente lavoro di classificazione diede origine nel 1924 all’Henry Draper Catalogue, contenente 255.000 stelle.

Per generare righe di assorbimento nel visibile (serie di Balmer = transizioni n ® 2, con n > 2) l’Idrogeno, che costituisce l’atmosfera di ogni stella, deve trovarsi in uno stato leggermente eccitato, con il suo unico elettrone nel secondo livello energetico (n = 2). Le stelle di tipo spettrale avanzato (late type) M sono troppo fredde per presentare l’idrogeno in questo stato, pertanto le righe di assorbimento dell’idrogeno cominciano a comparire solo nel tipo spettrale successivo (K) e diventano via via più intense fino al tipo spettrale A. Nelle stelle di tipo spettrale iniziale (early type) O e B le righe di assorbimento dell’idrogeno tornano a sparire, poiché l’elevata temperatura trasforma l’idrogeno neutro in idrogeno ionizzato.
L’Elio è invece un elemento chimico molto più stabile dell’idrogeno (si eccita e si ionizza con molta difficoltà), Per questo motivo le sue righe spettrali iniziano ad essere evidenti solo nelle classi O e B, dove la temperatura è sufficientemente elevata.
La maggior parte degli altri elementi, che gli astrofisici chiamano impropriamente metalli si eccitano e si ionizzano in genere con facilità. Così nei tipi spettrali avanzati M e K troviamo righe di composti molecolari (TiO) e di metalli neutri (Ca I - Calcio primo). Nei tipi spettrali intermedi compaiono le righe di metalli via via più ionizzati (Ca II, Ca III). Infine nei tipi spettrali iniziali (O e B) il grado di ionizzazione dei metalli è così elevato che le loro righe vanno a cadere nell’ultravioletto. In questo modo lo spettro visibile dei tipi spettrali O e B rimane piuttosto semplice, essendo caratterizzato solo dalle righe dell’idrogeno e dell’elio.

Lo studio degli spettri stellari ci ha permesso di determinare la composizione chimica media delle stelle. Se ci riferiamo alla percentuale di atomi dei diversi elementi, si trova che le stelle sono mediamente costituite da circa il 92% di Idrogeno, dall’8% di Elio, dallo 0,1% di Ossigeno, Carbonio, Azoto e Neon (in ordine di importanza) e solo dallo 0,01% di tutti gli altri elementi chimici.

La serie spettrale principale (OBAFGKM) è stata in seguito ampliata con serie secondarie introdotte per classificare stelle con spettri peculiari.
I tipi R ed N presentano la stessa temperatura rispettivamente dei tipi K ed M, ma un rapporto C/O ribaltato rispetto alla serie principale (dove è l’Ossigeno a prevalere sul Carbonio)
Il tipo S (stelle a Zirconio) hanno la stessa temperatura del tipo K, ma una netta prevalenza dell’ossido di Zirconio (ZrO) rispetto al più comune ossido di Titanio (TiO).
Il tipo W (o W-R: stelle di Wolf-Rayet) Sono caratterizzate da righe dell’Elio in emissione molto allargate, su spettri continui spostati verso la regione ultravioletta, a testimonianza di una temperatura superficiale estremamente elevata, che le pone a fianco o addirittura prima delle stelle di tipo O. Le righe allargate testimoniano una intensa perdita di massa per vento stellare (il gas emittente si sta espandendo radialmente: poiché una parte di esso si avvicina ed una parte si allontana ciascuna riga subisce contemporaneamente un red ed un blu-shift che la allarga). Si suddividono In due varietà: quelle ricche di Carbonio e povere di Azoto (WC) e quelle ricche di Azoto (WN).

 

Le stelle: evoluzione

Gli antichi ritenevano le stelle corpi celesti perfetti ed incorruttibili, costituiti da una materia peculiare (quintessenza) che le rendeva eterne. Le stelle subiscono in realtà processi di trasformazione come qualsiasi altro corpo materiale presente nell’universo, ma i loro tempi evolutivi sono enormemente superiori ai nostri tempi biologici.
Lo studio dell’evoluzione stellare si avvale di uno strumento fondamentale, il diagramma HR per rappresentare graficamente le trasformazioni fisiche cui vanno incontro le stelle durante la loro vita.

 

Il diagramma HR

All'inizio del '900 gli astronomi E. Hertzsprung e H. Russell, indipendentemente l'uno dall'altro, scoprirono che riportando in un diagramma le stelle, ordinate in base alla loro temperatura superficiale (tipo spettrale) ed alla loro magnitudine assoluta, se ne otteneva una distribuzione ordinata. Ponendo in ascisse i tipi spettrali o la temperatura superficiale in senso decrescente ed in ordinata la magnitudine assoluta decrescente (luminosità crescente), la maggior parte delle stelle (il 90% circa) si distribuisce lungo una linea curva che attraversa il diagramma diagonalmente dall’alto a sinistra, a destra in basso. Tale fascia è detta sequenza principale. Il sole si trova circa a metà della sequenza principale. Una piccola percentuale di stelle si concentra poi in due raggruppamenti isolati agli angoli opposti, in alto a destra e in basso a sinistra.
La concentrazione di stelle nella sequenza principale è in realtà perfettamente naturale e prevedibile sulla base della legge di Stefan-Boltzmann, in quanto l'emissione di energia, e quindi anche di energia luminosa, aumenta all'aumentare della temperatura superficiale della stella.
I due raggruppamenti isolati sembrano invece fare eccezione. In alto a destra si concentrano infatti stelle relativamente fredde, ma molto luminose, mentre in basso a sinistra stelle molto calde, ma poco luminose. La spiegazione può essere una soltanto. Dato che la temperatura superficiale delle stelle di tipo M in sequenza principale è la medesima delle stelle che si trovano in alto a destra, per la legge di Stefan-Boltzmann entrambe devono emettere la stessa quantità di energia per unità di superficie radiante. Le stelle in alto a destra, più luminose, devono quindi necessariamente emettere energia da una superficie più estesa. Esse sono quindi stelle fredde, ma molto grandi e per questo chiamate giganti rosse.

Analogo ragionamento vale per le stelle calde in basso a sinistra. Esse emettono la stessa quantità di energia delle stelle calde e luminose di tipo O e B della sequenza principale, essendo poco luminose devono perciò possedere una superficie radiante totale di piccole dimensioni e per questo motivo sono dette nane bianche.
Anche i diametri delle stelle in sequenza principale si presentano in modo caratteristico. Le stelle di sequenza principale più voluminose sono quelle in alto a sinistra (giganti bianco-azzurre). Il diametro decresce poi progressivamente lungo la sequenza principale fino alle stelle più piccole che si trovano in basso a destra (nane rosse).

Le giganti bianco-azzurre sono comunque più piccole delle giganti rosse, mentre le nane rosse sono più grandi delle nane bianche.
Le giganti bianco-azzurre sono anche le stelle più massicce della sequenza principale. La massa delle stelle decresce infatti progressivamente scendendo lungo la sequenza principale. Esiste d’altra parte una relazione di proporzionalità tra massa e luminosità intrinseca di una stella, nota come relazione di Eddington. Più massiccia è una stella e maggiore è la quantità di energia che le sue regioni centrali devono produrre per contrastare la forza gravitazionale che tenderebbe a far collassare la stella.
La relazione di Eddington afferma che la luminosità intrinseca è approssimativamente proporzionale alla potenza 3,5 della massa di una stella: L = k M3,5.
Tenendo presente che per il sole tale relazione può scriversi L3,5, dividendo membro a membro si ottiene una relazione in cui scompare la costante di proporzionalità e la luminosità e la massa delle stelle sono espresse in unità solari

Ad esempio una stella che presenti una massa doppia rispetto a quella del nostro sole (2 M

La relazione di Eddington è stata ottenuta sulla base di considerazioni teoriche basate sulle condizioni di equilibrio delle stelle, ma i valori che essa fornisce sono in buon accordo con quelli misurati direttamente per i sistemi di stelle doppie. La relazione di Eddington è valida esclusivamente per le stelle in sequenza principale.

Le classi di luminosità
In realtà la classificazione delle stelle in base alla loro luminosità è più articolata. Si è potuto notare che a parità di tipo spettrale le stelle presentano le righe di assorbimento del loro spettro più o meno allargate (una riga spettrale si caratterizza infatti anche per il suo profilo, cioè per il modo con cui l’intensità della riga diminuisce più o meno bruscamente ai suoi margini). Si ritiene che il fenomeno sia dovuto alla diversa pressione esercitata dal plasma che costituisce la stella (quando la pressione in un gas aumenta le sue righe tendono infatti ad allargarsi sempre più). Così le stelle che presentano atmosfere molto dense, caratterizzate da elevate pressioni presentano righe spettrali più allargate rispetto a stelle caratterizzate da atmosfere rarefatte. D’altra parte, poiché il livello di rarefazione delle atmosfere stellari è correlato con le dimensioni della stella (le stelle giganti sono molto rarefatte, mentre le nane sono molto compresse) e quindi con l’entità della superficie radiante, è possibile in tal modo ricavare informazioni sulla diversa luminosità a parità di tipo spettrale. In definitiva maggiori sono le dimensioni stellari, più il plasma è rarefatto (la sua pressione è bassa) e più le righe spettrali presentano un profilo a bassa dispersione (righe strette). Una minor larghezza delle righe spettrali è dunque indice di maggiori dimensioni stellari e quindi, a parità di temperatura, di maggiore luminosità.
Utilizzando tale criterio W.W. Morgan, P.C. Keenan e E. Kellman hanno introdotto nel 1937 un nuovo sistema di classificazione della luminosità delle stelle (Sistema MKK o MK) che suddivide le stelle in 8 classi di luminosità decrescente (0 - VII), distinguendo all’interno di ciascuna di esse 3 sottoclassi a ab b.

Classe                                                  Denominazione

                               0             0-Ia         Ia-0                                        Ipergiganti o Supergiganti estreme
Ia            Iab          Ib                                            Supergiganti
IIa           IIab         IIb                                           Giganti brillanti
IIIa          IIIab        IIIb                                          Giganti (normali)
IVa          IVab       IVb                                         Subgiganti
Va           Vab        Vb                                          Nane (Sequenza principale)
(VI)                         sd                           Subnane (pop.II)
(VII)                        D                            Nane bianche

 

Ricostruire i fenomeni associati alla nascita, alla vita ed alla morte di una stella non è impresa semplice, poiché l'evoluzione stellare si svolge in periodi di tempo lunghissimi che possono andare da qualche milione di anni per le stelle più massicce a qualche miliardo di anni per le stelle meno massicce. Così non è possibile osservare "in diretta" le trasformazioni di una stella, ma è necessario capire in quale fase evolutiva si trovano le diverse stelle che noi osserviamo e tentare di rimettere in sequenza i diversi fotogrammi. E' un po’ come scattare una fotografia di una comunità umana in cui compaiono neonati, bimbi, adulti e vecchi, cercando di capire a che fase della vita umana appartiene ciascuno di loro.
Le istantanee che noi possiamo scattare alle stelle sono rappresentate da punti del diagramma HR, il quale rappresenta perciò uno strumento fondamentale per interpretare l'evoluzione stellare. Si ritiene infatti che le modificazioni strutturali che una stella subisce durante la sua evoluzione si manifestino attraverso mutamenti nelle condizioni di temperatura e luminosità ed in definitiva con uno spostamento all'interno del diagramma HR. Naturalmente noi non abbiamo il tempo materiale per cogliere tali spostamenti all'interno del diagramma, ma possiamo cercare di interpretare il significato evolutivo di ciascun punto del diagramma.
Gli astrofisici cercano conferme dei loro modelli evolutivi nei diagrammi HR degli ammassi stellari. Essi ritengono infatti che le stelle di un ammasso si siano formate più o meno contemporaneamente da una stessa nebulosa. Avendo dunque la stessa età e la stessa composizione chimica, la diversa posizione assunta nel diagramma HR è funzione solo della massa delle diverse stelle. E’ pertanto possibile mettere in evidenza come stelle di diversa massa, trovandosi in punti differenti del diagramma, stiano attraversando  stadi diversi della loro evoluzione. Il numero di stelle che popola ciascuna zona del diagramma è inoltre proporzionale al tempo di permanenza della stella in quelle condizioni particolari di Temperatura e Luminosità. Zone scarsamente popolate del diagramma sono in genere punti di rapido passaggio, dove è pertanto poco probabile riuscire a cogliere stelle. Esistono tre tipi fondamentali di diagrammi di ammassi stellari, relativi rispettivamente alla fase di giovinezza, maturità e vecchiaia.

Per ottenere evidenze osservative sugli stadi iniziali dell’evoluzione stellare si studiano i diagrammi HR di gruppi di stelle che, trovandosi ancora immerse nella materia nebulare che le ha generate, testimoniano la loro giovane età. Tali aggregati sono costituiti soprattutto da stelle massicce (le più veloci a formarsi) di tipo spettrale O e B e sono detti associazioni OB.
Gli ammassi aperti e gli ammassi globulari vengono utilizzati invece per studiare rispettivamente le fasi di maturità e di vecchiaia
Gli ammassi aperti o di disco (Pleiadi, Jadi etc) sono aggregati contenenti da qualche centinaio a qualche migliaio di stelle che si collocano all'interno delle spire del disco galattico, mentre gli ammassi globulari o di alone sono enormi aggregati di stelle contenenti da 100.000 a qualche milione di stelle. Essi si dispongono a formare un enorme alone sferico che contiene il disco galattico, mentre sono assenti nel disco stesso. Nella nostra galassia ne sono stati contati poco più di un centinaio (circa 160).
Oltre alle osservazioni dirette, esistono anche numerosi modelli teorici, in cui le diverse fasi dell'evoluzione stellare vengono dedotte a partire dalle caratteristiche di massa e di composizione chimica di una stella e si fondano sui meccanismi di equilibrio interno e di produzione di energia che si ritiene siano alla base della struttura stellare. In particolare gli astrofisici ritengono che l'evoluzione stellare sia condizionata essenzialmente dalla massa iniziale della stella e dalla sua composizione chimica (teorema di Vogt-Russell).
La massa iniziale della stella ha effetto principalmente sulla sua velocità di evoluzione. Più massiccia è una stella, più rapidamente essa si forma, evolve e muore. La quantità di materia presente in una stella influenza in 2 modi diversi ed opposti la durata della sua vita. Da una parte più massiccia è una stella e tanta più materia essa ha a disposizione da poter trasformare in energia, secondo la relazione E = mc2. Dall'altra, all'aumentare della massa aumenta anche la velocità con cui la stella trasforma materia in energia secondo la relazione di Eddington. Per cui al crescere della massa l'energia a disposizione aumenta proporzionalmente, mentre l'energia utilizzata e dissipata cresce più che proporzionalmente. Possiamo quindi affermare che la stella è in grado di sopravvivere per un tempo che è direttamente proporzionale alla massa disponibile ed inversamente proporzionale alla velocità con la quale la massa viene trasformata in energia

I tempi di evoluzione di una stella decrescono quindi in modo esponenziale all'aumentare della massa.

 

Formazione stellare: fase di presequenza

Le stelle nascono dalla contrazione gravitazionale di gas e polveri che costituiscono le grandi nebulose, vere e proprie incubatrici stellari (nursery). Il meccanismo che innesca tale contrazione non è stato ancora chiarito. Tra le varie ipotesi vi sono le onde d'urto prodotte dall'esplosione di stelle massicce (supernovae), la collisione tra due o più nebulose ed altre ancora.

Durante la caduta gravitazionale del materiale nebulare l'energia potenziale si trasforma in energia cinetica con aumento progressivo di temperatura della protostella.
In questa prima fase, la cui durata dipende come sempre dalla massa in fase di contrazione, la temperatura superficiale è talmente bassa che la maggior parte dell'emissione avviene nell'infrarosso.
Nel 1947 vennero osservati e studiati all'interno di nebulose alcune strutture tondeggianti e dense di materia nebulare, con temperature estremamente basse (10°K) che risultarono essere tutte in fase di contrazione. Tali oggetti sono oggi noti come globuli di Bok e molti autori li ritengono probabili fasi iniziali nella formazione delle stelle.

Secondo i modelli teorici le protostelle nella loro fase iniziale dovrebbero essere circondate da un bozzolo di materia, compressa dal forte vento stellare, che si genera durante le prime fasi di vita. Il bozzolo, riscaldato dall'interno dovrebbe irradiare prevalentemente nell'infrarosso. Una probabile conferma di tale modello viene dall'oggetto Beklin-Neugebauer scoperto in Orione.

Le condizioni che permettono ad una condensazione di materia nebulare di mantenersi e collassare, invece di disperdersi, sono state studiate all'inizio del '900 da Jeans.  Se una nebulosa presenta una temperatura assoluta di T °K ed una densità di n atomi/cm3, essa collasserà solo se la sua massa è superiore alla cosiddetta massa di Jeans che, espressa in masse solari, vale

o, in alternativa, collasserà se il suo raggio è superiore al raggio di Jeans che, espresso in parsec, vale

Massa e Raggio di Jeans
Per il teorema del viriale una massa di gas autogravitante, in equilibrio dinamico tra la forza centrifuga e la forza centripeta, vale la relazione   .
Il numero di particelle presenti  si ottiene dividendo la massa totale M per la massa media di una particella.

Supponendo che ogni 100 particelle che compongono l'universo, 75 siano di Idrogeno (peso molecolare = 2) e 25 di Elio (peso atomico = 4), la massa media relativa (espressa in u.m.a.) sarà .
La massa media assoluta (espressa in grammi) di una particella si determina moltiplicando la massa relativa per il valore dell'unità di massa atomica (1,66 10-24 g/uma) .
L'energia cinetica totale diventa quindi . Applicando ora il teorema del viriale si ottiene

esprimendo il raggio R in funzione della densità () ed in definitiva

Mj è detta Massa di Jeans. Il suo valore, rispettivamente in grammi ed in masse solari, è approssimativamente 

Se esprimiamo la densità di materia come densità particellare, cioè come numero n di particelle per unità di volume () si ottiene rispettivamente

Se invece di esplicitare la massa esplicitiamo il raggio (dopo aver espresso la massa in funzione della densità) otteniamo

Tale quantità è detta Raggio di Jeans ed il suo valore, rispettivamente in centimetri ed in pc, è approssimativamente pari a

Se esprimiamo nuovamente la densità di materia come numero n di particelle per unità di volume () si ottiene rispettivamente

Durante la fase di contrazione la protostella è ovviamente più fredda di quanto sarà una volta giunta in sequenza principale, ma, possedendo una maggiore superficie radiante, è anche più luminosa. Come conseguenza di tali caratteristiche, le protostelle raggiungono la sequenza principale partendo dall’alto e le fasi di contrazione generano una traccia evolutiva che termina sul bordo sinistro della sequenza principale, nella regione detta Linea di età Zero o ZAMS (Zero Age Main Sequence).

Gli studi teorici prevedono che la contrazione gravitazionale di una protostella avvenga in 2 fasi. La prima, durante la quale l’interno della stella subisce un rimescolamento convettivo, produce nel diagramma HR una traccia verticale detta Linea di Hayashi. La seconda, durante la quale l’energia si propaga all’interno della stella prevalentemente in modo radiativo, produce una traccia orizzontale che si congiunge alla sequenza principale.

Una volta che all'interno della protostella si raggiungono temperature sufficientemente elevate si innescano le reazioni termonucleari che iniziano a contrastare la caduta del materiale nebulare verso il centro e generano le condizioni di equilibrio meccanico e termodinamico che stabilizzano la stella. Nelle fasi finali la stella neonata genera un intenso vento stellare (stadio T Tauri) che spazza gran parte della materia nebulare  che le orbita intorno. Il vento stellare risulta più efficace nella direzione dell’asse di rotazione della stella, dove gas e polveri sono meno spesse, essendosi depositate prevalentemente sul piano equatoriale. In alcuni casi è stato possibile osservare in stelle neonate  anelli di polveri circumstellari attraversati perpendicolarmente da getti di materia bipolare. Successivamente all’interno dei dischi di polvere nascerà il sistema planetario della nuova stella.

Il significato evolutivo della sequenza principale diventa allora chiaro. Essa rappresenta il punto del diagramma HR in cui le stelle consumano la maggior parte della loro vita, mantenendosi in equilibrio e trasformando all'interno del loro nucleo idrogeno in elio.  La scala temporale caratteristica per la contrazione gravitazionale di presequenza è detta tempo di Kelvin-Helmholtz. 
Per una nebulosa protostellare di densità particellare n, il tempo di Kelvin-Helmholtz (in anni) è

Come si può osservare il tempo di contrazione dipende solo dalla densità. Per una densità caratteristica delle nebulose di qualche centinaio di atomi per centimetro cubo i tempi caratteristici sono di circa 1 milione di anni. E’ probabile che durante la contrazione l’aumento della densità generi le condizioni per una frammentazione della massa nebulare in nuclei collassanti di dimensioni minori (all’aumentare della densità diminuisce la massa di Jeans). Ciò giustificherebbe il fatto che le stelle tendono a formarsi in gruppi o ammassi.

 

Tempo di Kelvin-Helmholtz
Una particella di massa m posta alla superficie di una nebulosa protostellare di massa M e raggio R è soggetta ad una forza gravitazionale 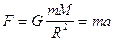, si ha
    

e integrando (dr è negativo poiché il moto in caduta avviene da quote maggiori a quote minori) si ottiene la velocità che anima la particella ad una distanza R dal centro  che, integrata, porge

esprimendo infine la massa in funzione della densità ed esplicitando il tempo, otteniamo

Tale quantità è nota come Tempo di Kelvin-Helmholtz e rappresenta la scala caratteristica dei tempi per la contrazione gravitazionale. Il suo valore, rispettivamente in secondi e in anni, (con r in g/cm3) è dell’ordine di

Se misuriamo infine la densità come numero di particelle per centimetro cubo (), si ottiene rispettivamente

Utilizzando i valori caratteristici delle nebulose T » 10 °K ed n » 102 - 104 particelle per centimetro cubo, si ottengono i seguenti valori        

La posizione assunta all'interno della sequenza e che poi viene mantenuta durante tutta la fase di stabilità dipende dalla massa stellare. Le stelle più massicce raggiungono più rapidamente la zona alta della sequenza diventando giganti bianco-azzurre, le stelle meno massicce raggiungono più lentamente la zona inferiore della sequenza diventando nane rosse. Naturalmente tutte le stelle con masse intermedie raggiungono una posizione intermedia che dipende dalla loro massa.
Gli astrofisici cercano conferme dei loro modelli evolutivi nei diagrammi HR degli ammassi stellari. Essi ritengono infatti che le stelle di un ammasso si siano formate più o meno contemporaneamente da una stessa nebulosa. Avendo dunque la stessa età e la stessa composizione chimica, la diversa posizione assunta nel diagramma HR è funzione solo della massa delle diverse stelle. E’ pertanto possibile mettere in evidenza come stelle di diversa massa si trovino in stadi diversi della loro evoluzione.
Per ottenere evidenze osservative sugli stadi iniziali dell’evoluzione stellare si studiano i diagrammi HR degli ammassi aperti e, in particolare, di gruppi di stelle che, trovandosi ancora immerse nella materia nebulare che le ha generate, testimoniano la loro giovane età.
Le stelle che si trovano nella vicina nebulosa di Orione sono da questo punto di vista un luogo privilegiato per studiare la nascita delle stelle. Lo studio dei movimenti reciproci (moti propri) ci conferma infatti che l’associazione stellare in Orione (associazione O-B) si sta disgregando. Le stelle si stanno allontanando reciprocamente, ma trovandosi ancora relativamente vicine le une alle altre, il processo deve essere iniziato solo da qualche milione di anni. Anche la presenza del gas nebulare intorno alle stelle, destinato a disperdersi in pochi milioni di anni, è un’ulteriore elemento  a favore della giovinezza di tali associazioni.

A conferma di quanto prevedono i modelli teorici, le stelle della nebulosa di Orione si distribuiscono per lo più al di sopra della sequenza principale, andando a formare un ventaglio più chiuso verso l'alto e più aperto verso il basso.

In altre parole nell'istantanea scattata tramite il diagramma HR abbiamo colto le stelle più massicce già arrivate in sequenza principale, mentre le stelle meno massicce sono ancora per strada. Partite insieme, le prime sono state più rapide, come previsto dalla teoria.

In realtà si calcola che non tutte le nebulose siano in grado di formare una stella. Se infatti la materia in fase di contrazione possiede una massa inferiore a circa 0,08 M. Alcuni ritengono che le nane brune potrebbero contribuire in modo sostanziale alla massa oscura degli aloni galattici. Nel 1993 sono stati individuati nell’alone della nostra galassia alcuni oggetti che agiscono come lenti gravitazionali (effetto microlensing) su stelle della Nube di Magellano e che potrebbero essere delle nane brune. Ad essi è stato dato il nome di MACHO (Massive And Compact Halo Object - Oggetti di Alone Massicci e Compatti).

L’effetto microlensing si produce quando la luce proveniente da una stella lontana viene deflessa dal campo gravitazionale di una piccola massa che le transita innanzi, quasi esattamente sulla congiungente stella-osservatore. I raggi luminosi vengono deviati e concentrati verso l’osservatore (lente gravitazionale) che percepisce un aumento  temporaneo della luminosità stellare. La probabilità di un tal evento è evidentemente molto piccola e dipende dal numero di oggetti interposti tra la stella e l’osservatore.

 

Fase di stabilità ed evoluzione finale

Le stelle rimangono in sequenza principale finché possiedono idrogeno nel loro nucleo da trasformare in elio attraverso il ciclo protone-protone ed il ciclo Carbonio-Azoto. Stelle con una massa pari a quella del sole impiegano 10 miliardi di anni.
Abbiamo già visto che la scala dei tempi evolutivi per una stella è ), possiamo tarare la relazione sul sole. La costante k assumerà infatti un valore pari al tempo di permanenza del sole in sequenza principale (1010 anni) e la relazione diventa pertanto


Ad esempio una stella con 5 M   esaurisce l'idrogeno del proprio nucleo ed esce dalla sequenza principale dopo circa 30 milioni di anni.
Quando la maggior parte dell'idrogeno si è trasformato in elio la stella esce dalla sequenza principale, avviandosi rapidamente (sempre in relazione alla sua massa) a concludere la sua vita.
Gli astrofisici distinguono a questo punto 3 possibili strade alternative per l'evoluzione stellare in funzione della massa. E' bene tener presente che i limiti di massa di seguito riportati sono puramente indicativi, essendo stati più volte ricalcolati e corretti.

1) Stelle di piccola massa (0,08 M)
Comprese tra il tipo spettrale M8 e G8, comprendono la maggior parte (circa il 90%) delle stelle di sequenza principale. Si presume che in tali stelle il movimento convettivo interno interessi tutta la massa stellare. Non esiste un vero nucleo e l'elio prodotto nelle regioni centrali più calde si mescola con gli strati esterni più freddi.
Quando le reazioni di fusione iniziano a rallentare per mancanza di idrogeno, l'intera stella comincia a collassare. La contrazione gravitazionale viene infine arrestata dal fenomeno della degenerazione elettronica. Quando infatti la materia viene compressa fino a densità dell'ordine di 106-108 g/cm3 (1-100 t/cm3), gli elettroni manifestano una violenta repulsione di natura quantistica, legata al principio di esclusione di Pauli. Gli elettroni sono infatti fermioni e non possono coesistere su di un medesimo livello energetico in numero superiore a 2 con spin antiparallelo.
Un modo alternativo per descrivere il fenomeno della degenerazione elettronica si ha facendo riferimento al carattere ondulatorio (lunghezza d’onda di De Broglie) delle particelle materiali.  Tenendo infatti presente che la lunghezza d’onda di De Broglie per una particella materiale vale λ = h/(mv), al diminuire della lunghezza d’onda (come conseguenza del collasso) deve aumentare la quantità di moto (mv), essendo h una costante (costante di Planck). L’aumento della quantità di moto mv comporta un aumento dell’energia cinetica (½ mv2) e quindi della pressione esercitata dagli elettroni.
Si forma in questo modo una stella di dimensioni planetarie, costituita al suo interno da materia allo stato degenere (gas di Fermi), rivestita da un sottile strato gassoso non degenere a temperature molto elevate (40.000-50.000°K). Tali stelle sono note come nane bianche.
Le nane bianche possono esistere come tali solo al di sotto di un certo limite di massa, detto limite di Chandrasekhar, pari a 1,44 M). Le nane bianche sono destinate a raffreddarsi in tempi lunghissimi, trasformandosi in nane nere (o nane brune).

2) Stelle di media massa ( 0,8 M ).
Comprese tra il tipo spettrale G8 e B3, comprendono circa il 10%) delle stelle di sequenza principale.
In queste stelle l'elio che si forma dalla fusione dell'idrogeno rimane confinato nel nucleo stellare. In tal modo quando le reazioni termonucleari iniziano a rallentare per scarsità di idrogeno e l'energia prodotta non è più sufficiente a contrastare la forza gravitazionale, la stella comincia a collassare.

Il nucleo di elio centrale viene compresso, si riscalda e raggiunge temperature dell'ordine del centinaio di milioni di gradi, sufficienti a innescare la fusione dell'elio, mentre gli strati superficiali, fortemente riscaldate, tornano ad espandersi, trovando un nuovo precario equilibrio a grande distanza dal centro. Si forma una stella enorme, dalla superficie esterna molto fredda (3.000-4.000°K), nota come gigante rossa.
La traccia evolutiva che nel diagramma HR sale verso la regione delle giganti rosse è detta Ramo delle Giganti Rosse (Red Giant Branch - RGB).

Il processo di fusione dell’elio è detto ciclo del triplo elio o 3a,  in cui tre nuclei di elio si fondono per formare un nucleo di carbonio ed un fotone energetico.

Secondariamente il Carbonio può assorbire un altro nucleo di elio e trasformarsi in Ossigeno

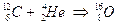
Contemporaneamente un sottile strato di idrogeno al di sopra del nucleo raggiunge le temperature necessarie per fondere idrogeno in elio. Si formano così due strati concentrici a livello dei quali viene prodotta energia mediante fusioni di diverso tipo.
Le stelle rimangono in stadio di gigante rossa per tempi molto brevi se paragonati alla durata della loro permanenza in sequenza principale. L'efficienza delle reazioni di fusione di elementi più pesanti dell'idrogeno diminuisce infatti progressivamente. Già la fusione dell'Elio in Carbonio presenta un difetto di massa dello 0,065% contro lo 0,7% della fusione dell'Idrogeno in Elio.

L'Elio ha massa 4,0026 uma e quindi 3 atomi di Elio 12,0078 uma, mentre il Carbonio 12 pesa 12 uma. Il difetto di massa è pari a 12,0078 - 12 = 0,0078 uma. Il valore percentuale è quindi 0,0078/12,0078 = 0,00065.

Durante le reazioni di fusione si generano anche neutroni liberi che sono responsabili della formazione di elementi chimici più pesanti, attraverso i cosiddetti processi-s, in cui un nucleo cattura un neutrone e subisce un decadimento beta aumentando il suo numero atomico.

Vengono definiti processi-s (da slow = lento) le reazioni di assorbimento neutronico da parte di un nucleo, in presenza di una densità di neutroni relativamente bassa. In queste condizioni il neutrone catturato ha il tempo di decadere (decadimento b) prima che un nuovo neutrone venga assorbito.
La presenza negli spettri stellari delle righe del Tecnezio (Tc) rappresenta una delle migliori conferme dell’esistenza della nucleosintesi stellare e dei processi-s. Il Tecnezio non ha infatti isotopi stabili (non esiste sulla terra). Anche il più stabile, il Tc-98, ha un tempo di dimezzamento di due milioni di anni.

Quando l’Elio del nucleo comincia ad esaurirsi e l'energia prodotta torna a diminuire la forza gravitazionale prevale ancora e la stella collassa nuovamente.

Le stelle di media massa non sono però in grado di comprimere ulteriormente la materia al loro interno, in quanto vengono raggiunte densità tali che la degenerazione elettronica è in grado di contrastare la forza gravitazionale. All'interno della gigante rossa si forma in modo quiescente (senza eventi esplosivi) una nana bianca. Inizialmente la nana bianca è oscurata dal guscio di gas e polveri che forma gli strati più esterni della gigante rossa.
Poiché le nane bianche possono esistere come tali solo al del limite di Chandrasekhar, pari a 1,44 M, gli astrofisici ritengono che durante l'evoluzione quiescente da gigante rossa a nana bianca, la stella debba espellere, sotto forma di un intenso vento stellare, buona parte della sua massa iniziale.
Ciò contribuisce a sospingere ad una certa distanza dalla nana bianca l'inviluppo gassoso, il quale va  a formare una specie di guscio opaco a circa 1 anno luce dal centro. La materia che compone tale guscio, eccitata dalla radiazione emessa dalla nana bianca,  diventa visibile emettendo per fluorescenza (emissione su lunghezze d'onda superiori a quelle assorbite) prima di disperdersi nello spazio.
Oggi si ritiene che gli oggetti celesti che verso la fine del '700 Herschel aveva denominato nebulose planeterie per il loro aspetto sferico e compatto, rappresentino appunto tale fase di transizione di stelle di media massa, da giganti rosse a nane bianche. L’estrema rarefazione delle nebulose planetarie (103 particelle per cm3) è responsabile della formazione di alcune righe proibite (ad esempio le due intense righe verdi a 4959 Å e 5007 Å dell’OIII), inizialmente attribuite ad elementi chimici sconosciuti (come il nebulio o il coronium individuato nella corona solare).

Le righe proibite sono dovute a transizioni elettroniche estremamente poco probabili nelle condizioni di densità del gas raggiungibili nei laboratori terrestri, dove l’elevata frequenza degli urti tra le particelle porta a continue eccitazioni e diseccitazioni collisionali. Nelle atmosfere rarefatte delle nebulose planetarie, dopo che una particella si è eccitata a causa di un urto, un secondo urto è poco probabile e la diseccitazione può avvenire tramite emissione di radiazione.

Conferme di tale modello teorico vengono ancora una volta dall'analisi dei diagrammi HR di gruppi di stelle omogenee per età, quali sono quelle che formano i cosiddetti ammassi stellari. Come abbiamo già detto gli astrofisici ritengono che le stelle di un ammasso abbiano approssimativamente la stessa età e la stessa composizione chimica. In conseguenza di ciò, la diversa posizione assunta nel diagramma HR deve essere funzione solo della massa delle diverse stelle. Nella nostra galassia esistono due tipi fondamentali di ammassi: gli ammassi aperti (o di disco) e gli ammassi globulari (o di alone).

I diagrammi HR degli ammassi aperti  presentano tutti la sequenza principale interrotta nella sua parte superiore. Nel punto di interruzione le stelle piegano verso destra, andando a formare un uncino detto punto di svolta o turn-off point. Qui il diagramma manca quasi completamente di stelle (lacuna di Hertzsprung) per poi riprendere nella regione delle giganti rosse.
Mettendo a confronto diagrammi HR di ammassi diversi si osserva che la posizione del punto di svolta è diversa da ammasso ad ammasso.

Gli astrofisici interpretano tali diagrammi come una conferma delle loro teorie sull'evoluzione stellare. Il punto di svolta coglie infatti le stelle che stanno lasciando la sequenza principale per trasformarsi in giganti rosse. Naturalmente le stelle più massicce, che si sono evolute più rapidamente, si sono già trasformate in giganti rosse e mancano quindi dalla sequenza principale. In tal modo ammassi che presentano un punto di svolta molto basso debbono essere ritenuti più vecchi, in quanto anche stelle di massa minore hanno già lasciato la sequenza principale per trasformarsi in giganti rosse. Esiste una relazione tra posizione del punto di svolta ed età dell'ammasso stellare.
La lacuna di Hertzsprung si giustifica con il fatto che la transizione dalla sequenza principale alla zona delle giganti rosse è talmente rapida che è molto poco probabile cogliere le stelle in questa fase.
La lacuna di Hertzsprung non è comunque completamente priva di stelle. E' infatti proprio qui che possiamo trovare le variabili intrinseche come le "cefeidi" e le variabili di tipo "Mira", a testimonianza del fatto che la transizione avviene attraverso delle vistose modificazioni degli equilibri interni della stella.

I diagrammi HR degli ammassi globulari mostrano tutti punti di svolta estremamente bassi, con la sequenza principale ridotta praticamente alle nane rosse (subnane), a testimonianza del fatto che si tratta di aggregati di stelle estremamente vecchie. Si calcola che essi abbiano oltre 10 miliardi di anni.

Nel 1942 Baade accertò una sostanziale differenza nei tipi spettrali e nella composizione chimica delle stelle appartenenti agli ammassi aperti rispetto alle stelle appartenenti agli ammassi globulari.
Infatti mentre le stelle degli ammassi globulari risultarono composte essenzialmente da idrogeno ed elio, le stelle degli ammassi aperti (e delle altre stelle appartenenti al disco galattico, come il sole) contenevano anche quantità più o meno apprezzabili di tutti gli altri elementi chimici (che gli astrofisici chiamano in modo improprio "metalli"). Baade suddivise così le stelle in due popolazioni. Le stelle come il sole, contenenti anche metalli furono dette stelle di popolazione I, le stelle senza metalli come quelle degli ammassi globulari, stelle di popolazione II.

Oggi gli astronomi ritengono che le due popolazioni stellari siano il prodotto di diverse generazioni stellari. In altre parole le stelle di popolazione II, prive di elementi più pesanti si sarebbero formate per prime all'interno della galassia, quando ancora gli unici elementi a disposizione erano l'idrogeno e l'elio formatisi durante il Big Bang (nucleosintesi primordiale). Esse rappresentano dunque la prima generazione stellare. Quando poi le stelle più massicce di prima generazione hanno arricchito le nebulose galattiche di elementi più pesanti attraverso esplosioni di supernovae, le successive generazioni stellari hanno prodotto stelle  ricche di 'metalli', classificate come stelle di popolazione I. Esse costituiscono quindi stelle di seconda generazione o, in generale, stelle di generazioni successiva alla prima.
I diagramma HR di ammassi globulari sono quindi diversi dai diagrammi HR degli ammassi aperti, sia per la differenza di età che si esprime in una diversa posizione del punto di svolta (molto più bassa), sia per la diversa composizione chimica. Ricordiamo infatti che, per il teorema di Vogt-Russell, il tipo di evoluzione stellare dipende esclusivamente dalla massa e dalla composizione chimica. Gli astrofisici ritengono ad esempio che il cosiddetto ramo orizzontale che compare nei diagrammi HR degli ammassi globulari sia da mettere in relazione proprio alla loro diversa composizione chimica. Si tratta di una sequenza quasi orizzontale di stelle che congiunge la zona delle giganti rosse con la parte mediana della sequenza principale.

Gli astrofisici ritengono che essa sia prodotta dal fatto che le stelle, dopo essersi trasformate in giganti rosse, mutano rapidamente le loro caratteristiche di temperatura e luminosità, ritornando al centro della sequenza principale. Da qui si ritrasformano lentamente in giganti rosse, producendo il ramo orizzontale.
Nel braccio orizzontale si trovano le cefeidi del tipo RR Lyrae (e le W Virginis), a testimonianza del fatto che la trasformazione avviene attraverso condizioni di non equilibrio.
Un'altra caratteristica dei diagrammi HR degli ammassi globulari è l'assenza della lacuna di Hertzsprung. Le stelle poco massicce rimaste in sequenza principale si trasformano infatti in giganti rosse in modo talmente lento che diventa probabile coglierle in tutte le fasi intermedie del loro percorso ed esse si uniscono quindi alla zona delle giganti rosse con un tratto continuo. Le stelle di sequenza di popolazione II sono inoltre leggermente meno luminose (classe VI di luminosità = subnane) dei corrispondenti tipi spettrali di popolazione I (classe V di luminosità = nane).

• Stelle di grande massa (8M).

Stelle di tipo spettrale O e B (fino a B3), comprendono meno dell’1%) delle stelle di sequenza principale. Quando l’idrogeno del nucleo si è trasformato in Elio e non viene più prodotta energia sufficiente per contrastare la forza gravitazionale, la stella collassa e comprime il suo nucleo di elio fino ad innescarne la fusione. Contemporaneamente un guscio esterno di Idrogeno raggiunge la temperatura di fusione, mentre gli strati più superficiali si espandono enormemente fino a trasformare la stella in una supergigante, con dimensioni che possono raggiungere 1000 volte quelle del sole.
Quando il nucleo di Elio si sarà trasformato in un nucleo di C/O ed il guscio esterno di idrogeno si sarà trasformato in Elio, la produzione di energia comincerà a diminuire, costringendo la stella a collassare nuovamente. Durante questa contrazione, le stelle di grande massa sono in grado di portare le temperature del loro nucleo a valori intorno ai 2 miliardi di gradi, sufficienti per innescare la fusione del Carbonio, con formazione di Neon e Magnesio . Contemporaneamente Il guscio esterno di Elio si riaccende per dare Carbonio e Ossigeno, mentre un terzo guscio si aggiungerà ai primi due dove l'idrogeno sarà in grado di formare elio.
Ogni qual volta l’energia si esaurisce il meccanismo si ripete e ciascun guscio fonde per dare elementi più pesanti, mentre un nuovo guscio si aggiunge esternamente.
Nello stadio successivo l’Ossigeno fonde producendo prevalentemente Silicio e Zolfo In questo modo all'interno dell'enorme e rarefatto inviluppo gassoso che caratterizza una supergigante, si produce una struttura annidata a cipolla, densa e compatta, formata da strati concentrici, caratterizzati da temperature e densità crescenti verso il centro, in cui si producono per fusione elementi sempre più pesanti.

 

Abbondanze cosmiche degli elementi e nucleosintesi
Fred Hoyle fu il primo ad intuire che che gli elementi chimici potessero formarsi nelle stelle durante la loro evoluzione. Insieme a William Fowler e ai coniugi Margaret e Geoffrey Burbidge (scherzosamente riuniti nella sigla HB2F), mise a punto i primi modelli di nucleosintesi stellari (1957). Il loro pionieristico lavoro venne in seguito esteso e perfezionato con la collaborazione di R.W. Wagoner (1967).
I modelli teorici elaborati per prevedere i processi di nucleosintesi stellare (cioè quali elementi chimici, ed in che proporzioni, si formino durante l’evoluzione di una stella) sono in grado di giustificare in modo molto soddisfacente le percentuali cosmiche osservate (abbondanze relative) degli elementi chimici, con l’eccezione dell’Idrogeno e dell’Elio. L’origine di questi ultimi è da ritenersi cosmologica e le loro abbondanze ben si accordano, come vedremo, con quelle previste dai modelli elaborati per la nascita dell’universo (Big Bang e relativi processi di nucleosintesi primordiale).
Da questo punto di vista la composizione chimica dell’universo può essere considerata una testimonianza “archeologica” della sua storia evolutiva, un reperto fossile cruciale dove sono registrate le trasformazioni cui è stata sottoposta la materia dalla sua nascita ad oggi.
L’elemento di gran lunga più diffuso nell’universo è l’Idrogeno (» 73% in peso), seguito dall’Elio (» 25% in peso) e da tutti gli altri elementi chimici (» 2% in peso) con al primo posto l’Ossigeno seguito da C, N, Ne, S, Si, Fe.
Ogni 100.000 atomi di Idrogeno ve ne sono 8.500 di Elio, 65 di Ossigeno, 35 di Carbonio, 20 di Azoto.
In generale l’abbondanza relativa di un elemento chimico nell’universo diminuisce all’aumentare del suo numero atomico Z. Troviamo però alcune interessanti regolarità: gli elementi con Z dispari sono meno frequenti dei loro vicini con Z pari e si evidenziano inoltre picchi di frequenza in corrispondenza degli elementi con numero di massa A multiplo intero di 4 (massa dell’Elio) come C-12, O-16, Ne-20, Mg-24, Si-28, S-32, Ar-36, Ca-40, Ti-48, Cr-52, Fe-56, Ni-60.
Tali regolarità si spiegano facilmente ricordando che l’Elio (Z = 2 e A = 4) rappresenta il mattone fondamentale con il quale vengono costruiti per successiva fusione gran parte degli elementi più pesanti.

La produzione di energia in queste fusioni è però via via inferiore, poiché sempre minore risulta il difetto di massa. Il limite di questo processo risulta essere lo stadio del ferro, poiché la fusione del ferro per formare nuclei più massicci richiede energia (reazione endoergonica) invece di produrla.
Così invece di contrastare il collasso gravitazionale la fusione del ferro lo accelera. Ne segue una fase di implosione delle regioni centrali della stella.
Il nucleo centrale di Ferro crolla su se stesso con una velocità che si calcola essere circa un quarto di quella della luce. L'energia gravitazionale in tal modo liberata produce una immensa onda d'urto che spazza via le regioni più esterne, in una esplosione di elevatissima potenza detta supernova (di tipo II). Gli strati più esterni della stella, investiti da un'enorme quantità di energia, la utilizzano per produrre elementi di peso atomico superiore tramite processi-r, di cattura rapida di neutroni. E' così che le supernovae arricchiscono l'universo di tutti gli elementi chimici, anche quelli più pesanti, formando nuove nebulose, dalla contrazione delle quali nascono successive generazioni stellari.

Vengono definiti processi-r (da rapid = rapido) le reazioni di assorbimento neutronico da parte di un nucleo, in presenza di una elevata densità di neutroni. In queste condizioni il neutrone catturato non ha il tempo di decadere (decadimento b) prima che un nuovo neutrone venga assorbito ed in tal modo il nucleo può rapidamente aumentare il suo numero di massa.

Una supernova è in grado di produrre luce quanto una piccola galassia, presenta infatti in media una magnitudine assoluta pari a M = -18. La prima supernova ad essere avvistata e di cui abbiamo notizia dalle cronache cinesi e giapponesi, fu la supernova del 1054 d.C. nella costellazione del Toro, che rimase visibile in pieno giorno per alcune settimane.
In tempi più recenti sono state avvistate nella nostra galassia soltanto altre due supernovae. Quella studiata da Tycho Brahe nel 1572 e quella di Keplero del 1604.
Ormai sono quasi quattro secoli che non esplode più una supernova nella nostra galassia e gli astronomi sono costretti a studiare le supernovae che esplodono in galassie esterne. Moltissime informazioni sono state ottenute dalla supernova esplosa nel 1987 nella grande Nube di Magellano, una piccola galassia, satellite della nostra. L'esplosione di una supernova produce una enorme nube di gas e polveri in espansione. Particolarmente studiata la nebulosa del Granchio (Crab Nebula), prodotta dalla supernova del 1054 ed ancor oggi perfettamente visibile.
La parte centrale della stella, che ha subito il collasso, può evolvere secondo tre modelli diversi in funzione della massa residua, andando a formare diverse classi di oggetti collassati. Se la massa che rimane dopo l'esplosione è inferiore 1,44 M si forma un buco nero.

 

Evoluzione stelle doppie: binarie cataclismiche (novae e supernovae Ia)

Quando in un sistema di stelle doppie le due stelle possiedono masse diverse e sono sufficientemente vicine (doppie strette) da riuscire, in opportune condizioni, a rubarsi reciprocamente materia, si producono fenomeni particolari di evoluzione stellare. La stella di massa maggiore, indicata come primaria, subisce infatti un'evoluzione più rapida e diventa una gigante rossa quando la stella meno massiccia, indicata come secondaria, è ancora in sequenza principale.
A questo punto, se le stelle sono sufficientemente vicine, parte dell'inviluppo gassoso della gigante rossa cade sulla stella secondaria, accelerandone l'evoluzione.
Col procedere dell'evoluzione la stella primaria si trasformerà in una nana bianca mentre la secondaria diverrà a sua volta una gigante rossa. Successivamente il flusso di materia è destinato ad invertirsi e parte dell'inviluppo gassoso della secondaria cadrà sulla nana bianca (primaria). La materia entrando in orbita intorno alla nana bianca forma un anello di accrescimento. Nel punto in cui il flusso di materia urta l'anello di accrezione si produce un forte aumento di temperatura che si manifesta tramite una macchia luminosa (macchia calda). Quando la materia che si accumula sulla superficie della nana bianca raggiunge la temperatura di fusione essa esplode come un'atomica. L’esplosione è così violenta che la  luminosità della stella aumenta fino a 150.000 volte in poche ore.
I primi fenomeni di questo tipo furono inizialmente interpretati come l'accensione di una nuova stella in cielo. La prima nova fu osservata, secondo quanto narra Plinio, da Ipparco nel 143 a.C. Fino ad oggi ne sono state osservate qualche centinaio, non tutte ugualmente splendenti.

Spesso il fenomeno della nova non giunge a distruggere il sistema binario, per cui la stella secondaria può continuare a perdere materia a favore della primaria fino ad una nuova esplosione che in genere si manifesta ogni 10 - 20 anni (novae ricorrenti). A differenza delle novae non ricorrenti che manifestano magnitudini assolute molto diverse, le nove ricorrenti presentano tutte la stessa magnitudine assoluta  (M = -7,5) e rappresentano pertanto dei buoni indicatori di distanza.

In alcuni casi invece il fenomeno risulta particolarmente violento e l'aumento di luminosità (M = - 20) diventa addirittura superiore a quello delle supernovae di II tipo (M = - 18). Gli astronomi indicano queste esplosioni come supernovae di  tipo Ia  e ritengono che in tal caso il sistema stellare  ne risulti completamente distrutto. Si ritiene che ciò avvenga quando la nana bianca si trova al limite di Chandrasekhar. L’ulteriore acquisto di materia avvia un collasso gravitazionale che innesca una reazione di fusione esplosiva nelle regioni centrali della stella.
Tipicamente la luminosità di una supernova di tipo Ia raggiunge il massimo in circa tre settimane per poi diminuire progressivamente nell’arco di alcuni mesi. Presentano una luminosità massima che varia leggermente da caso a caso, ma che è ben correlata con la durata dell’esplosione (periodo di aumento della luminosità). Le esplosioni più lunghe sono caratterizzate da una maggiore luminosità. Misurando la durata del periodo esplosivo è quindi possibile effettuare le opportune correzioni e calcolare la luminosità intrinseca con un errore che attualmente si stima essere intorno al 10%. Ciò fa delle supernovae di tipo Ia le candele campione meglio calibrate ed attualmente più utilizzate. Le supernovae di tipo Ia esplodono in una galassia mediamente ogni 300 anni.

Le supernove di tipo Ib non presentano nei loro spettri le righe dell’Idrogeno. Si ritiene che le supernove di tipo Ib siano prodotte da esplosioni analoghe alle supernove di tipo II, in cui l’inviluppo gassoso superficiale di Idrogeno sia stato in qualche modo asportato.

 

 

Le stelle: Oggetti collassati

 

Stelle a neutroni e pulsar

Le stelle a neutroni si formano quando la forza gravitazionale è talmente intensa da vincere la repulsione elettronica associata alla materia degenere. Gli elettroni vengono spinti all'interno dei nuclei atomici dove si uniscono ai protoni per trasformarsi in un neutrone ed un neutrino.  In queste condizioni la stella diventa un unico enorme nucleo atomico formato solo da neutroni in cui la densità è enorme, dell'ordine di 1015 - 1017 g/cm3 (1-100 miliardi di tonnellate).

Le stelle a neutroni  presentano densità dello stesso ordine di grandezza della densità dei nuclei atomici. Un nucleo ha massa dell’ordine di 10-24 g, dimensioni dell’ordine di 10-13 cm  e volume dell’ordine (10-13)3 = 10-39 cm3. La densità è pertanto dell’ordine di 10-24/10-39 = 1015 g/cm3.

Le stelle a neutroni presentano un diametro caratteristico di una decina di chilometri. Dovendo poi rispettare la legge della costanza del momento angolare, con il procedere del collasso (diminuzione del raggio) la velocità di rotazione della stella aumenta progressivamente fino a raggiungere valori estremamente elevati.
L'esistenza delle stelle a neutroni venne ipotizzata teoricamente nel 1932 da L.D. Landau. Nel 1934 Zwicky suggerì che una stella a neutroni potesse formarsi in certe condizioni come residuo dell'esplosione di una supernova.
Per poter confermare l'esistenza delle stelle a neutroni è necessario attendere la scoperta negli anni '60 delle pulsar.
La prima pulsar, una sorgente celeste che emetteva impulsi radio ad intervalli regolari di 1,3 secondi, venne scoperta nel 1967 dai radioastronomi di Cambridge. I giornali parlarono addirittura di extraterrestri che tentavano di comunicare con noi.
Gli astrofisici ritenevano invece si trattasse di una stella in rapidissima rotazione (per l'appunto un giro ogni 1,3 secondi) in grado di inviare un segnale radio ad ogni rotazione (modello a faro). Naturalmente solo stelle sufficientemente piccole e dense da non essere mandate in pezzi dalle enorme forza centrifuga, potevano ruotare ad una tale velocità. La maggior parte degli astrofisici pensava ad una stella a neutroni e la conferma arrivò l'anno successivo.
Gli astronomi pensarono infatti che se le pulsar erano effettivamente stelle a neutroni e le stelle a neutroni si formavano come residuo di un'esplosione di supernova, allora si sarebbe forse potuto scoprire una pulsar al centro della nebulosa del Granchio.
Nel 1968 si scoprì che la nebulosa del Granchio conteneva una velocissima pulsar che emetteva un segnale ogni 33 millisecondi (circa 30 giri al secondo). Si trattò di una notevole conferma sia della natura delle pulsar che del modello di evoluzione di una supernova.
Si ritiene che l'emissione degli impulsi radio regolari da parte di una pulsar sia dovuto al campo magnetico estremamente intenso associato alla stella, il cui asse non coincide con l'asse di rotazione della stella. In tal modo la stella ruotando costringe l'asse magnetico ed il campo stesso a compiere un rapido movimento doppio conico. L'intenso campo magnetico rotante cattura e trascina in rapida rotazione il plasma stellare, con produzione di fasci rotanti di radiazione.
Nel caso la massa residua in via di collasso ecceda il limite di Oppenheimer-Volkov nemmeno i neutroni riescono ad arrestare l'implosione e tutta la materia si concentra in un punto a densità infinita. La stella si trasforma in un buco nero. 

 

Buchi neri

Un buco nero è un oggetto nei cui dintorni la gravità è talmente elevata da non permettere nemmeno alla luce di evadere. Tale comportamento si manifesta fino ad una certa distanza critica, detta  raggio di Schwarzschild.

Per calcolare il raggio di Schwarzschild consideriamo che la velocità che un corpo di massa "m" deve possedere per vincere l'attrazione gravitazionale di un altro corpo di massa maggiore "M",  detta velocità di fuga può essere calcolata eguagliando l'energia cinetica all'energia gravitazionale (Ecin = Egrav)

da cui la velocità di fuga risulta pari a

Dunque se, a parità di massa M, il raggio R della stella diminuisce, la velocità di fuga deve aumentare. Poiché in un buco nero il raggio è destinato ad azzerarsi la velocità di fuga tende ad infinito. Quando, durante la contrazione, la velocità di fuga diventa uguale alla velocità della luce,

il raggio assume un valore critico, pari a

Tale raggio è detto appunto raggio di Schwarzschild. Esso viene dunque definito come il raggio entro il quale una data massa deve essere compressa affinché la velocità di fuga eguagli la velocità della luce.
Per una stella della massa del sole il raggio di Schwarzschild assume il valore di 3 km, per la terra di 1 cm.

Nel caso dell'implosione di una supernova di II tipo la materia continua la sua caduta fino a densità infinita. La superficie sferica individuata dal raggio di Schwarzschild ha comunque una sua importanza fisica e viene detta orizzonte degli eventi. Infatti, poiché non esiste nessun corpo in grado di raggiungere la velocità della luce, nessun corpo che si trovi all'interno dell'orizzonte degli eventi possiede velocità sufficiente per uscirvi. Ciò vale anche per la radiazione elettromagnetica che all'interno dell'orizzonte possiede una velocità inferiore alla velocità di fuga. Nessuna informazione ci può perciò giungere dall'interno dell'orizzonte degli eventi che circonda un buco nero.

Da un punto di vista teorico sono possibili anche buchi neri a densità finita.  Se infatti aumenta la massa del corpo in fase di collasso gravitazionale, aumenta anche il raggio di Schwarzschild. In queste condizioni un oggetto può raggiungere il suo raggio di Schwarzschild in corrispondenza di una densità relativamente bassa.
Eleviamo al cubo il raggio di Schwarzschild ed esprimiamolo in funzione della densità , ottenendo

Se ad esempio una galassia di piccole dimensioni, poniamo di 108 masse solari, collassasse fino al suo raggio di Schwarzschild, potrebbe formare un buco nero di circa 2 U.A. (se fosse al posto del sole arriverebbe oltre Marte) e con la densità dell'acqua.
La speranza di osservare un buco nero è oggi riposta sull'eventualità che uno di essi si trovi all'interno di un sistema binario. In tal caso potremmo osservare una stella che sta ruotando intorno ad un "nulla" che presenta le caratteristiche di massa di un buco nero. Inoltre il buco nero sarebbe in grado di fagocitare la stella compagna, rubandole materia. Cadendo all'interno del buco nero tale materia sarebbe destinata, secondo gli astrofisici, a ruotare in modo vorticoso in una spirale sempre più stretta, riscaldandosi fino a temperature molto elevate con emissione di una tipica radiazione nella banda dei raggi X. Gli astrofisici ritengono ad esempio che la sorgente di raggi X nella costellazione del Cigno, nota come Cignus X-1, potrebbe essere prodotta da un buco nero. Un buco nero che fagocita materia rappresenta il più efficiente meccanismo di produzione di energia, dopo il processo di annichilazione materia-antimateria. La sua efficienza può giungere fino al 50% contro lo 0,7% del ciclo p-p.

Infatti, un corpo di massa m che da grande distanza (idealmente da distanza infinita, dove l’energia potenziale è nulla) si avvicina fino a distanza R ad un corpo di massa M, è in grado di liberare una quantità di energia gravitazionale pari a

Se ora sostituiamo ad R il raggio di Schwarzschild, otterremo l'energia che la particella di massa m può arrivare a dissipare durante la sua caduta verso un buco nero fino all'orizzonte degli eventi

Come si vede metà della massa della particella può essere trasformata in energia con un'efficienza massima del 50%.

Nessun oggetto materiale può giungere indenne al centro di un buco nero. Durante il percorso esso subisce infatti delle violente sollecitazioni interne (effetti mareali) che tendono ad allungarlo nel senso di caduta, fino a ridurlo in brandelli. Si tratta delle stesse forze che sulla terra producono le maree, allungando l’idrosfera lungo l’asse Terra-Luna. Le forze mareali sono un effetto della differente attrazione gravitazionale cui sono sottoposti punti diversi di uno stesso corpo. Esse sono dunque proporzionali non al valore della gravità in un certo punto, ma alla differenza di gravità esistente tra due punti.

Consideriamo un corpo di lunghezza 2L e massa m che stia cadendo verso un buco nero di massa M. Quando si trova a distanza d dal centro del buco nero, esso è sottoposto ad una forza gravitazionale .
Ma nel medesimo istante, i punti A e C, che si trovano ai due estremi del corpo a distanza rispettivamente minore ().
Il punto A possiede quindi una maggior accelerazione rispetto a B, pari a

mentre il punto C è soggetto ad un’accelerazione inferiore e pari a

In altre parole mentre nel baricentro B vi è corrispondenza tra forza applicata e accelerazione generata, questo non accade negli altri punti. Qui infatti l’accelerazione tende a rimanere la stessa che si ha nel baricentro (il corpo è infatti rigido e tutti i suoi punti si muovono in modo solidale), mentre la forza applicata risulta diversa per la diversa distanza dal centro di attrazione.
Si determinano pertanto delle tensioni interne che tendono ad allungare il corpo ed i cui effetti in un certo punto sono evidentemente proporzionali alla differenza tra la gravità nel punto e la gravità al baricentro. Calcoliamo ad esempio l’accelerazione differenziale (e quindi anche la corrispondente forza mareale) a cui è sottoposto il punto A.

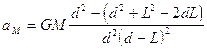
nell’ipotesi che le dimensioni del corpo siano trascurabili rispetto alla distanza che lo separa dal centro di attrazione () possiamo omettere nelle somme sia L (rispetto a d), che L2 (rispetto a d2), ottenendo il seguente risultato approssimato

dove si dimostra che le forze mareali sono direttamente proporzionali alla distanza L del punto dal suo baricentro ed inversamente proporzionali al cubo della distanza d del baricentro dal centro di attrazione. Naturalmente all’altra estremità il corpo sarà sottoposto ad una forza eguale e contraria.
In un buco nero, dove la gravità raggiunge valori elevatissimi, le differenze di gravità su dislivelli anche molto piccoli diventano talmente elevate da produrre la completa disgregazione in senso radiale dei corpi in caduta. Ad esempio l’intensità delle forze mareali per unità di massa (quindi l’accelerazione) in corrispondenza del raggio di Schwarzschild è pari a

Se per ipotesi il Sole (M = 2 1033 g) si trasformasse in un buco nero, un uomo dell’altezza di 2 m subirebbe, attraversando l’orizzonte degli eventi, un effetto mareale dell’ordine di 1012 cm/s2. La testa ed i piedi verrebbero strappate in direzione opposta con un’accelerazione 1 miliardo di volte superiore alla normale accelerazione di gravità.

Fino a non molto tempo fa si riteneva che un buco nero potesse solo accrescersi inglobando altra materia. Recentemente Hawking ha dimostrato che la superficie di un buco nero può dare fenomeni di "evaporazione quantistica" legati al principio di indeterminazione di Heisenberg.

 

Il Mezzo interstellare

Un tempo si riteneva che lo spazio galattico interstellare fosse praticamente vuoto. Oggi l’esistenza di materiale diffuso tra gli oggetti condensati (stelle, pianeti etc) è stata definitivamente accertata sulla base di innumerevoli evidenze osservative.  Il mezzo interstellare (ISM – interstellar medium) costituisce circa il 10-15 % della massa galattica ed è composto per il 99% circa (in massa) di gas e per il rimanente 1% di polvere.

 

Polvere

La polvere è formata da particelle solide di minuscole dimensioni (0,1 - 1 m), costituite prevalentemente di grafite, solfuro di carbonio (CS), silicati e ghiacci. Ciascuna particella è mediamente formata da 108 atomi. La densità media è di 100 particelle di polvere per km3 (10-13 particelle per cm3). L’effetto principale della polvere è quello di assorbire e, soprattutto, di diffondere (scattering) la luce. Ciò provoca una diminuzione della luminosità delle stelle che prende il nome di estinzione interstellare. L’estinzione dipende naturalmente dalla quantità di polvere interposta e di conseguenza anche dalla distanza della stella.
Si calcola che mediamente vi sia una diminuzione di magnitudine apparente pari a 1-2 gradi per kpc.

La luce che proviene dal centro della galassia, posto a circa 10 kpc, subisce una diminuzione molto più elevata di circa 27/28 gradi di magnitudine. In altre parole dal centro della galassia ci arriva solo 1 fotone ogni 100 miliardi. Infatti, se il rapporto tra flusso percepito ed flusso in assenza di estinzione è 1/1011, applicando la relazione di Pogson si ottiene )

Inoltre per le loro dimensioni i granuli diffondono prevalentemente la luce a minor lunghezza d’onda (luce blu) e per questo motivo le stelle appaiono sistematicamente più rosse (più corretto sarebbe dire “meno blu”) di quanto ci si potrebbe aspettare sulla base del loro tipo spettrale (arrossamento interstellare o reddening). Si tratta dello stesso fenomeno che arrossa il sole all’alba e al tramonto, quando la sua radiazione deve attraversare uno strato più spesso di atmosfera
Essendo l’entità dell’arrossamento proporzionale alla quantità di polvere interposta, esso è di conseguenza correlabile al grado di estinzione. Ciò permette agli astronomi di apportare le opportune correzioni alla luminosità, sulla base del livello di arrossamento.

La differenza tra l’indice di colore (B-V) osservato e quello teorico fornisce un parametro noto come eccesso di colore EB-V. Maggiore è l’arrossamento, minore il flusso nel blu, maggiore la magnitudine nel blu B, maggiore l’indice di colore osservato e, di conseguenza, più elevato l’eccesso di colore. L’eccesso di colore è correlato all’estinzione (o assorbimento, absorption) AV nella banda del visibile V, dalla relazione 

 

Gas

Il gas è costituito essenzialmente da idrogeno (73% in massa), elio (25% in massa) e da minime percentuali di altri elementi (2% - in prevalenza O, C, N, Ne, S, Si, Fe).
Presenta una densità media di 1 particella per centimetro cubo La pressione è circa 1025 volte inferiore a quella atmosferica.

I diversi elementi possono presentarsi, a seconda delle condizioni termodinamiche del gas sia in forma atomica (neutra o ionizzata) che in forma molecolare.
In particolare l’idrogeno si presenta in forma:

• ionizzata (Regioni H II)
• atomica (idrogeno neutro o Regioni H I)
• molecolare (H2)

L’idrogeno neutro (atomico) e quello ionizzato si osservano facilmente.
L’idrogeno neutro (HI) emette una riga di 21 cm, il secondo emette nel visibile la tipica radiazione rossa della serie di Balmer (riga Ha) dell’idrogeno eccitato. L’idrogeno molecolare è invece difficile da osservare direttamente e per rilevarlo si utilizza come sonda la molecola di CO (la seconda molecola per abbondanza dopo l’idrogeno molecolare - CO/H2 = 1/105), la quale viene eccitata ed emette proprio grazie agli urti con l’H2 un’intensa riga di 2,6 mm (ed a 1,3 mm).

 

Distribuzione

Gas e polveri si concentrano prevalentemente sul piano galattico ed in particolare sulle braccia della spirale, dove presentano una concentrazione dieci volte maggiore rispetto allo spazio interbraccia.
Le braccia sono disegnate da nubi di idrogeno atomico diffuso (regioni HI) punteggiate da densi agglomerati di idrogeno molecolare (nubi molecolari giganti)

• Il 50% circa del mezzo interstellare si trova diffuso nelle spire a formare le cosiddette regioni HI dell’idrogeno neutro (atomico), con una densità particellare intorno a 10 particelle/cm3 ed una temperatura dell’ordine di 102 °K. Come si ricorderà fu proprio la mappatura di tale gas (Edward Purcell e Harold Ewen – 1951) a permettere di disegnare la forma a spirale della nostra galassia.

 

• Il rimanente 50% va a costituire le cosiddette nubi molecolari giganti (o complessi molecolari giganti GMC), enormi strutture gravitazionalmente legate, immerse nelle vaste regioni HI. Manifestano un’elevata estinzione per la presenza di elevate quantità di polveri, che proteggono le sostanze allo stato molecolare dagli effetti distruttivi della radiazione ad alta frequenza (UV, X, gamma etc). Sono costituite in primo luogo da idrogeno molecolare, ma in esse si trova una grande varietà di altre specie chimiche molecolari. La temperatura relativamente bassa (10 K) e la elevata densità (rn » 103/104  cm-3) ne fanno i luoghi ideali per la formazione stellare. Nonostante presentino una maggior pressione rispetto al gas che le circonda, sono sostanzialmente stabili e non si espandono essendo probabilmente corpi autogravitanti. Dopo gli ammassi globulari, sono gli oggetti più massicci esistenti nella nostra galassia, con masse dell’ordine di 105/106 M. Finora ne sono state contate circa 6.000. Al loro interno la materia nebulare può interagire in modo diverso con la radiazione proveniente dalle stelle, diventando osservabile nel visibile e formando in tal modo tre tipi fondamentali di nebulose: oscure, in emissione, in riflessione. Alcune nebulose sono note fin dall'antichità. Quella di Orione è ad esempio visibile ad occhio nudo quando il cielo è particolarmente terso. A differenza delle stelle che presentano sempre un aspetto puntiforme, a qualsiasi ingrandimento, le nebulose ci appaiono come macchie di luce diffusa (altre come macchie scure sul cielo stellato). In passato il basso potere di risoluzione dei telescopi non permetteva di distinguere una nebulosa da una galassia ed il termine “nebulosa” veniva utilizzato per indicare indifferentemente qualsiasi oggetto dall’aspetto diffuso, non puntiforme.

• Le nubi oscure sono caratterizzate da una densità che decresce radialmente in modo omogeneo dall’interno verso l’esterno. Sono individuabili per l’elevata estinzione che producono sulle stelle retrostanti e si manifestano pertanto come macchie scure sul fondo stellato. Presentano dimensioni di pochi parsec (5-10 pc) e masse pari a 102-103 M . Quando le dimensioni non superano il parsec sono dette globuli.  Quando si presentano come striature scure allungate sono dette proboscidi.

 

• Le nebulose in emissione sono regioni di idrogeno ionizzato (regioni H II) da stelle giovani e massicce (ammassi aperti giovani, associazioni O-B), che presentano la tipica colorazione rossastra dell’idrogeno in emissione. La dimensione di una regione HII (Raggio di Strömgren) e la sua luminosità dipendono dal tipo spettrale (e quindi dalla temperatura) della stella eccitante. Le regioni H II possono essere per questo motivo utilizzate come indicatori di distanza. La pressione molto elevata che caratterizza le regioni HII (T » 104 °K ; rn » 102/103  cm-3) ne fa delle strutture non in equilibrio e dunque in espansione, destinate a dissolversi nel giro di qualche milione di anni. La bassa densità particellare è responsabile (come avviene anche nelle nebulose planetarie) della formazione di righe proibite.

• Se le stelle che si formano sono più fredde, il gas e le polveri circostanti diffondono e riflettono la radiazione emessa, producendo nebulose in riflessione. Poiché le radiazioni diffuse con maggior efficienza sono quelle a minor lunghezza d’onda, le nebulose a riflessione presentano caratteristici colori bluastri (il cielo diurno è azzurro per la stessa ragione).

 

Recentemente si è scoperto che l’idrogeno atomico che forma le spire (Regioni HI) è in equilibrio di pressione con altre due fasi gassose:

• Un mezzo internebulare caldo, che separa le regioni HI, con una densità particellare intorno a 10-1 particelle/cm3 ed una temperatura dell’ordine di 104 °K. Costituisce circa il 50% del volume del mezzo interstellare;
• Un gas coronale caldissimo, che si estende fuori dal disco galattico fino all’alone, con una densità particellare intorno a 10-3 particelle/cm3 ed una temperatura dell’ordine di 106 °K. Pur contenendo una minima frazione della massa, costituisce circa il rimanente 50% del volume del mezzo interstellare. È stato scoperto nel 1976 da E.B.Jenkins e D.M. Elmegreen e si ritiene possa essersi formato al passaggio delle onde d’urto delle esplosioni di supernova.

Come si diceva, le tre fasi sono in reciproco in equilibrio, non evidenziando alcuna tendenza ad espandersi l’una a spese dell’altra. Ciò dipende dal fatto che esse presentano sostanzialmente i medesimi valori di pressione, come si può dedurre dal fatto che il prodotto della densità particellare per la temperatura risulta sempre costante.
Ricordando infatti che la costante di Boltzmann (k = 1.380658 10-23 j k-1)) è pari al rapporto tra costante R dei gas e numero N di Avogadro, sostituendo opportunamente nell’equazione di stato dei gas perfetti si otterrà

osservando ora che nN/V è il numero di particelle per unità di volume o densità particellare (rn), possiamo scrivere

dove si dimostra che i gas in cui è costante il prodotto (rn T), presentano la stessa pressione.

La pressione del mezzo interstellare risulta quindi 1025 volte inferiore alla pressione atmosferica (1 atm = 101325 pascal).

 

La Galassia: Via Lattea

 

Il sole, le stelle, le nebulose, gli ammassi stellari sono raggruppati dalla forza di gravità in una struttura alla quale diamo il nome di Galassia. La nostra non è l'unica galassia a popolare l'universo, ma questa certezza ci deriva da scoperte relativamente recenti.
Agli inizi del nostro secolo si riteneva che la nostra galassia rappresentasse da sola l'intero cosmo o addirittura, per una certa ripugnanza a considerarla completamente circondata dallo spazio vuoto, che le stelle fossero distribuite in modo uniforme per tutto l'universo.
Il primo a concepire l'idea che le stelle possedessero una qualche particolare distribuzione nel cosmo fu T. Wright. Nel 1750 Wright ipotizzò che le stelle fossero disposte su di una lastra circolare di spessore finito. Herschel dette verso la fine del '700 consistenza scientifica a tale ipotesi, attraverso un lungo e paziente conteggio delle stelle che giunse a dimostrare come esse fossero più frequenti nella direzione del disco galattico che nella direzione ad esso perpendicolare. Egli propose correttamente di interpretare la Via Lattea come una zona di cielo in cui le stelle apparivano più concentrate essendo disposte sul piano galattico e suggerì un rapporto spessore/diametro di 1/5.

All’inizio del ‘900 l’olandese Jacobus Kapteyn (1901), utilizzando e perfezionando le tecniche di conteggio stellare introdotte da Herschel stimò per la prima volta le dimensioni del disco galattico (26.000 x 6.500 al), ponendo però il sole quasi al centro del sistema.

Un'idea più concreta sulla reale struttura della galassia, sulle sue dimensioni e sulla posizione del sole al suo interno si iniziò ad avere solo nel 1918 quando H. Shapley, utilizzando le cefeidi presenti negli ammassi globulari, ne determinò la distanza e scoprì che presentavano una distribuzione sferica. Egli propose correttamente che il centro della galassia dovesse coincidere con il baricentro dell'alone galattico costituito dagli ammassi globulari. Emerse allora che il sole non si trovava, come molti ritenevano, al centro della galassia, ma a circa 3/5 del raggio.

Shapley non poteva però sapere che le cefeidi degli ammassi globulari erano RR Lyrae, molto meno luminose delle cefeidi classiche. In tal modo egli sovrastimò le distanze degli ammassi globulari e la nostra galassia risultò erroneamente possedere dimensioni eccessive (250.000 al). In questo modo sembrava che tutti gli oggetti osservabili rientrassero nei limiti della galassia  ed in definitiva che quest’ultima fosse l’unica struttura dell’universo.

A tale ipotesi era nettamente contrario H.D.Curtis, il quale aveva stimato in un milione di anni luce la distanza della nebulosa di Andromeda e riteneva pertanto che si trattasse di una struttura che, come molte altre, si trovasse al di fuori della nostra galassia.

Si accese una grande disputa che divise in due fazioni il mondo accademico sulla unicità o meno della nostra galassia nell’universo.
Il primo a congetturare che alcune nebulose osservate nella nostra galassia fossero in realtà esse stesse galassie esterne alla nostra (universi-isola) fu Kant nel 1755. Naturalmente ciò rimase per molto tempo una pura supposizione fino a quando nel 1923 Hubble riuscì a risolvere, con il telescopio di 2,5 metri di Monte Wilson, la nebulosa di Andromeda in stelle separate ed identificò nelle sue spire alcune Cefeidi che gli permisero di calcolarne la distanza. Essa si rivelò di gran lunga maggiore di quella di qualsiasi altro corpo celeste fino ad allora osservato all'interno della nostra galassia. La nebulosa di Andromeda era diventata la galassia di Andromeda, la prima galassia ad essere osservata. Una galassia a spirale con la materia che si concentrava in spire su di un disco galattico.
Nel 1927 Lindblad e Oort dimostrarono, attraverso l'analisi dei red-shift e dei blu-shift stellari, che la nostra galassia ruotava intorno al centro galattico.

Il sole ad esempio compie una rivoluzione completa intorno al centro galattico in circa 200 milioni di anni con una velocità di circa 250 km/s.

Il moto delle stelle nella galassia
Il moto rispetto al sole delle stelle appartenenti alla nostra galassia può essere evidenziato misurandone separatamente la componente radiale e la componente tangenziale. La componente radiale (Vr = cz) è la più semplice da misurare in quanto produce uno spostamento delle righe spettrali osservate (red o blu-shift). La componente trasversale (moto proprio) è evidenziabile solo per stelle sufficientemente vicine a noi da produrre spostamenti significativi sulla volta celeste.

Tale componente si misura in frazioni di secondi d'arco all’anno (moto proprio m in arcsec/anno) e solo conoscendo anche la distanza della stella d è possibile convertire tale velocità angolare in una velocità lineare trasversale (Vt = m d). Si tenga presente che è necessario convertire l’unità di misura del moto proprio da arcsec/anno in rad/s e la distanza d da parsec in km in modo che la velocità trasversale venga data in km/s.

dove, 206.265 è il numero di secondi di grado contenuti in un radiante (ed anche il numero di unità astronomiche contenute in un parsec) e 31.557.600 è il numero di secondi di tempo contenuti in un anno giuliano di 365,25 giorni. In definitiva si avrà

Quando sono note entrambe queste componenti sarà evidentemente possibile calcolare la velocità risultante (Vs = Velocità spaziale). Si tenga presente comunque che, poiché sia il sole che le stelle sono in movimento rispetto al centro galattico, la velocità spaziale rappresenta la velocità della stella rispetto al sole (supposto fermo).La velocità spaziale rappresenta quindi la differenza tra la velocità della stella (Vst) e la velocità del sole (Vso) misurate rispetto al centro della galassia.

Se prendiamo in considerazione le velocità spaziali delle stelle che si trovano nelle immediate vicinanze del sole, abbiamo l’impressione che il sole presenti un moto di traslazione verso un punto della costellazione di Ercole detto apice solare (di coordinate equatoriali a = 270°  d = + 30°), alla velocità di circa 19,5 km/s. Tale moto si manifesta tramite la sola componente radiale: un blu-shift per le stelle prossime alla posizione dell’apice ed un red-shift per le stelle in posizione opposta (anti-apice), mentre le stelle che si trovano in posizione laterale non presentano alcuna componente radiale, ma solo dei moti propri.

 

Nel 1951 venne infine la conferma che anche la nostra è una galassia a spirale come Andromeda. Il risultato fu acquisito grazie ad un lavoro di mappatura dell'idrogeno neutro presente nel disco galattico (iniziato da Edward Purcell e Harold Ewen). L'idrogeno è infatti l'elemento di gran lunga più diffuso nell'universo. Negli spazi interstellari esso si trova a bassissima temperatura come idrogeno neutro. Nel suo stato fondamentale il protone e l'elettrone dell'idrogeno si presentano con spin antiparalleli. Assorbendo una minima quantità di energia l'idrogeno passa in uno stato eccitato, in cui protone ed elettrone possiedono spin paralleli. Quando infine l'idrogeno ritorna nel suo stato fondamentale emette una caratteristica riga spettrale di 21 cm (come previsto nel 1944 dall’olandese Hendrik  van de Hulst).
Tale radiazione non è naturalmente osservabile con un normale telescopio ottico, ma con un radiotelescopio opportunamente sintonizzato. Inoltre su tale lunghezza d'onda non si hanno fortunatamente i fenomeni di diffusione ed interferenza da parte della enorme quantità di polveri concentrati nel disco galattico che rendono ardua l'osservazione ottica.
L'idrogeno neutro del disco galattico è stato in tal modo accuratamente mappato e se ne è potuta osservare una caratteristica distribuzione in spire.

Negli anni '60 e '70 sono stati scoperti gli spettri di altre molecole nello spazio interstellare, come quello dell'ammoniaca (NH3), della formaldeide (H2CO), dell'ossido di carbonio (CO) etc.
Ma probabilmente la scoperta che fece più scalpore fu quella dell'acido formico (HCOOH) e della metilammina (CH3NH2), le quali reagendo sono in grado di formare il più semplice degli aminoacidi, la glicina.

Tutti i dati raccolti fino ad oggi ci permettono di tracciare un modello galattico piuttosto attendibile.
La nostra galassia ha dunque la forma di un disco del diametro di circa 100.000 anni luce. Lo spessore del disco è mediamente di 1500 anni luce, ma in prossimità del centro è presente un rigonfiamento detto bulbo (bulge) o nucleo galattico che presenta uno spessore di circa 15.000 anni luce. Il disco galattico è racchiuso in un guscio sferico di ammassi globulari, in cui la materia interstellare (gas e polveri) è estremamente rarefatta.
La maggior parte della materia (stelle, ammassi aperti, materia interstellare) è infatti distribuita in spire all'interno del disco galattico.
Le spire ruotano sul piano galattico nella stessa direzione delle stelle, ma con velocità inferiore (circa la metà) rispetto ad esse. Secondo i modelli attuali le spire sarebbero quindi delle semplici onde di densità della materia, luoghi in cui il "traffico stellare" risulta momentaneamente rallentato e quindi più intenso. Il modo in cui i bracci a spirale si formano e sopravvivono è tuttavia ancora oggetto di studio e l'esistenza di molti modelli alternativi che tentano di risolvere il problema dimostra come la soluzione non appaia ancora a portata di mano.
Gli astrofisici hanno stimato la massa galattica in 200 miliardi di M. Conoscendo infatti la massa del sole, la sua distanza dal centro galattico e trattando la galassia come un sistema kepleriano è possibile utilizzare la terza legge di Keplero.

Data l'incertezza dei dati a disposizione possiamo effettuare un'analisi dimensionale, limitandoci agli ordini di grandezza.
La massa del sole è pari a Ms  2 1033 g
La sua distanza dal centro galattico è D  3 104 al 3 1022 cm
Il suo periodo di rivoluzione è Ps  2 108 anni 6 1015 s
applicando la terza di Keplero

esplicitiamo la massa della galassia MG

Dividendo infine per la massa del sole si ottiene appunto la massa galattica in masse solari, pari 2 1011 M

Ciò naturalmente non significa che la galassia possieda 200 miliardi di stelle, poiché molta materia non si trova concentrata nelle stelle, ma nelle polveri e nei gas interstellari. Si stima quindi che la galassia contenga circa 100 miliardi di stelle e che la massa rimanente sia presente sotto forma di materia diffusa o collassata.
Recentemente alcuni dati sembrano indicare la presenza intorno alla galassia di un enorme alone di materia oscura (non luminosa) che manifesta i suoi effetti gravitazionali modificando il comportamento dinamico della rotazione galattica.

Le misure effettuate sulla massa luminosa di molte galassie indicano un rapporto medio M/L dell'ordine di 10 – 20 M.

La densità media delle stelle nella nostra galassia è stimata attorno a  10-2 al-3, pari a circa 1 stella per ogni 100 anni-luce cubici, che equivale ad una distanza media di circa 5 anni-luce tra stella e stella. Se infatti la distanza media tra due stelle è d, il numero di stelle per unità di lunghezza è 1/d, il numero di stelle per unità di superficie è 1/d2 ed il numero di stelle per unità di volume (rS) è 1/d3. Se ne deduce pertanto che in un aggregato tridimensionale di elementi la distanza che media che li separa è pari a

La misura della parallasse ha permesso di individuare circa 6700 stelle in un raggio di 55 al. Utilizzando tale dato è possibile stimare la densità delle stelle comprese in una sfera di 55 al di raggio.

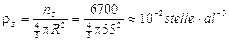
Approssimando ora la galassia con un disco di raggio R = 50.000 al e spessore medio h = 1.500 al, il volume galattico sarà R2h ed il numero totale N di stelle contenute nella nostra galassia sarà dunque pari al volume galattico per il numero di stelle contenute nell'unità di volume

In ottimo accordo con le stime dinamiche.

 

Le Galassie

 

Andromeda è la galassia a noi più vicina, poco più di 2 milioni di anni luce, e molto simile alla nostra galassia per massa e struttura. Oltre ad Andromeda l'universo risulta popolato a distanze sempre maggiori da un numero enorme di galassie. Si stima ne esistano oltre un centinaio di miliardi.

 

Morfologia e classificazione

In base alla loro forma le galassie sono classificate in spirali, ellittiche ed irregolari.
In alcune galassie a spirale le spire non partono dal nucleo galattico ma dall'estremità di un segmento di materia che attraversa il nucleo stesso e per questo motivo sono dette spirali barrate.
Un tempo si pensava che le galassie nascessero come ellittiche per poi trasformarsi in spirali (Hubble). Oggi si ritiene invece che la struttura della galassia dipenda essenzialmente dalle particolari condizioni dinamiche e cinematiche della nube protogalattica.
Secondo gli astrofisici infatti le galassie si sarebbero formate dalla frammentazione del gas primordiale in  immense condensazioni nebulari (protogalassie), ciascuna  in rotazione intorno ad un proprio asse e soggette ad un moto di contrazione gravitazionale.
Se le velocità di rotazione e di contrazione della nube protogalattica sono tali per cui la materia che sedimenta sul piano del disco ha il tempo per essere totalmente utilizzata nella formazione di stelle di alone di prima generazione, si dovrebbe formare una galassia ellittica. In caso contrario parte della materia nebulare, arricchita di elementi pesanti dall'esplosione delle supernovae più massicce, raggiunge il piano contribuendo a formare galassie a spirale.

 

Galassie peculiari: Nuclei Galattici Attivi (AGN)

Gli AGN (Active Galactic Nuclei) costituiscono un gruppo di oggetti celesti, caratterizzati da luminosità estremamente elevate (fino a 1015 L) e da una emissione non termica (non di corpo nero).
Si manifestano in modi diversi, ma oggi si ritiene che possano essere ricondotti ad un comune modello galattico.
Gli astrofisici ritengono infatti che tutti gli oggetti classificati come AGN siano galassie con i nuclei interessati da fenomeni esplosivi di enormi proporzioni di cui non conosciamo la natura. Il candidato più probabile a fungere da motore centrale (central engine) per gli AGN dovrebbe essere il solito enorme buco nero. Dal nucleo galattico si dipartono getti di materia luminosa che si allontanano in direzione perpendicolare al disco galattico (jets). Il nucleo è inoltre circondato da nubi emittenti di gas e polveri in espansione indicate come BLR (Broad Lines Region = regione a linee allargate) e NLR (Narrow Lines Region = regione a linee sottili).

La larghezza delle righe in emissione è correlabile con la velocità di espansione del gas. Se la materia si espande in tutte le direzioni, parte di essa si avvicina e una parte si allontana dall’osservatore, in modo che ciascuna riga subisce contemporaneamente un red ed un blu-shift che la allarga.

Secondo il modello unificato i diversi tipi di AGN possono essere spiegati facendo riferimento alla differente angolazione con cui un AGN viene osservato.
Alcuni tra gli oggetti classificati come AGN sono le galassie di Seyfert, le Radiogalassie, i Blazar e i Quasar. Le Galassie Star-burst sono galassie peculiari a volte impropriamente classificate come AGN. Si tratta di galassie in cui l’elevata luminosità è sostenuta da un eccezionale tasso di formazione stellare (star-burst), probabilmente innescato da uno scontro con un’altra galassia. Il loro spettro ottico è molto simile a quello delle regioni HII.

Le  galassie di Seyfert, sono galassie a spirale caratterizzate dalla presenza di un nucleo puntiforme, di aspetto stellare, particolarmente brillante.

Le radiogalassie sono galassie ellittiche che presentano un’emissione radio paragonabile a quella ottica e quindi fino ad un milione di volte più intensa di quella emessa nella stessa banda dalle galassie normali. L'emissione radio è concentrata in due enormi lobi che si trovano in posizione opposta rispetto alla galassia, uniti ad essa da sottili filamenti. Le onde radio sono generate dal movimento spiraleggiante del plasma intorno alle linee di forza del campo magnetico (emissione di sincrotrone).

I Blazar (ing. blaze = vampata) sono caratterizzati da una luminosità fortemente e rapidamente variabile, con periodi inferiori al giorno. Si suddividono in oggetti BL Lac (BL Lacertae) e in OVV (Optical Violently Variable).

I Quasar o QSO vennero osservati per la prima volta nel 1962. Inizialmente essi furono identificati attraverso un'emissione radio intensissima e fortemente concentrata. In seguito, puntando i telescopi ottici su di essi, venne rilevata anche una sorgente luminosa dall'aspetto stellare, puntiforme. Ciononostante, l'analisi dello spettro confermò che non poteva assolutamente trattarsi di stelle. Si coniò allora il termine di "oggetti quasi stellari" o Quasi Stellar Objects (QSO o Quasar).
In un secondo tempo vennero scoperti oggetti analoghi, ma radioquieti, anch'essi classificati come quasar.
Gli spettri dei quasar non furono immediatamente riconosciuti finché non si tentò di interpretarli come spettri fortemente spostati verso il rosso.
Se i quasar sono oggetti così distanti, come la maggior parte degli astronomi ritiene, un semplice calcolo dimostra che la loro luminosità intrinseca deve essere enorme, superiore a quella di un'intera galassia.
Ma il dato più sconcertante fu la scoperta che alcuni quasar presentavano una luminosità variabile.
Da una parte è infatti piuttosto improbabile che un'intera galassia di stelle produca una variazione sincrona della luminosità di tutte le sue componenti.
In secondo luogo è possibile dimostrare che se le dimensioni di un oggetto luminoso sono maggiori della lunghezza cT, dove T è il periodo di variabilità della luminosità, un osservatore non sarebbe in grado di percepirne la variabilità. Ciò ha come conseguenza che se un quasar presenta, come spesso avviene, un periodo di variabilità della sua luminosità di  un mese, esso non può possedere un diametro superiore ad un mese-luce.
Eppure da una regione così minuscola, comparabile alle dimensioni del sistema solare, viene emessa una quantità di energia maggiore di quella emessa da un'intera galassia.
Gli astronomi si chiedono quale meccanismo possa produrre una quantità così elevata di energia in un volume così piccolo. Forse enormi buchi neri che stanno inghiottendo materia? Oggi si ritiene che i quasar siano i nuclei attivi di galassie così lontane da non poter essere osservate. Ma la grande lontananza dei quasar pone anche un problema evolutivo.
Forse è possibile ipotizzare una relazione tra quasar, radiogalassie e galassie normali, per cui i primi rappresenterebbero forme primordiali di aggregazione della materia (ricordiamo che i quasar essendo molto distanti nello spazio, sono anche molto distanti nel tempo) destinati ad evolversi e a trasformarsi nelle odierne strutture galattiche? Tutte domande in attesa di risposta, problemi sui quali dibatte oggi la cosmologia moderna.

 

Distribuzione: la struttura a grande scala dell’universo

 

Alcune galassie appaiono talmente vicine da far supporre l'esistenza tra di esse di un legame gravitazionale. L'esistenza di ammassi di galassie (cluster) è stata ipotizzata negli anni Trenta da Fritz Zwicky e da lui stesso poco dopo confermata con la scoperta dell’enorme ammasso in Coma (Chioma di Berenice). Glia ammassi formati da qualche decina di galassie sono detti gruppi.
La nostra galassia appartiene ad un piccolo ammasso formato da una ventina di galassie (quasi tutte ellittiche nane) che ruotano intorno ad un baricentro comune. Tale ammasso è detto Gruppo Locale. 
Il Gruppo Locale appartiene all'ammasso della Vergine, comprendente 2500 galassie (quasi tutte a spirale). Analizzando i red-shift delle galassie appartenenti al Gruppo Locale e all'ammasso della Vergine a cui esso appartiene è stato possibile evidenziare un movimento di caduta del Gruppo Locale verso il Centro dell'ammasso della Vergine  alla velocità di circa 220 km/s.
Ragionando in termini di ordine di grandezza, un ammasso tipico è una struttura delle dimensioni di 10 Mpc contenente 103 galassie, con una densità dell’ordine di 1 galassia per Mpc3 ed una distanza media tra galassie di 1 Mpc. Le stime dinamiche della massa (massa del viriale) è dell’ordine di 1015 masse solari, circa 1 ordine di grandezza più elevata della semplice somma delle masse delle singole galassie. Gli ammassi presentano pertanto tipicamente un rapporto M/L dell’ordine di 300h M.

L’esistenza di raggruppamenti di ordine superiore, i superammassi (supercluster), formati da aggregati gravitazionali di ammassi di galassie, fu ipotizzata nel 1953 da Gerard de Vaucouleurs. Le sue osservazioni lo indussero a ritenere che il Gruppo Locale, l’ammasso in Ercole, l’ammasso in Coma e l’ammasso in Vergine fossero gravitazionalmente legati a formare una enorme struttura appiattita (Superammasso Locale) di cui l’ammasso in Vergine costituiva il centro. L’ipotesi di de Vaucouleurs tardò ad essere accettata, ma i dati osservativi non sembrano lasciare dubbi sull’esistenza del Superammasso Locale e di numerose altre analoghe strutture. Le prime conferme vennero nel 1959 con il lavoro di classificazione eseguito da George Abell su 2712 ammassi, le cui posizioni suggerivano chiaramente una loro distribuzione non omogenea nello spazio ed in seguito con i lavori di mappatura bidimensionale di Jim Peebles e tridimensionale di Margaret Geller e John Huchra. I superammassi sono tra loro separati da immensi spazi vuoti (voids). L'universo su grande scala mostra oggi una struttura spugnosa, con gli ammassi ed i superammassi che si distribuiscono in enormi filamenti e superfici curve, aventi uno spessore minore di un decimo delle loro dimensioni, che racchiudono bolle di spazio prive, almeno apparentemente, di materia luminosa delle dimensioni di 100 Mpc. Riuscire a giustificare una tale distribuzione di materia è oggi uno dei problemi centrali della cosmologia.
Sempre in termini di ordine di grandezza, un superammasso tipico è una struttura delle dimensioni di 100 Mpc contenente una decina di ammassi, tra loro separati da  una distanza media di qualche decina di Megaparsec. La massa è dell’ordine di 1016 M, con un rapporto M/L analogo a quello misurato per i singoli ammassi.

La distribuzione di materia nell'universo appare estremamente irregolare su piccola scala. Ma l'omogeneità cresce con la scala, tanto che gli astronomi sono convinti che l'universo possa considerarsi fondamentalmente omogeneo ed isotropo a grandissima scala, cioè su distanze superiori ai 100 Mpc.

Recenti lavori di conteggio di galassie hanno evidenziato una densità media delle galassie dell’ordine di 10-2 Mpc-3 (vedi “L’origine della struttura dell’universo” in Le Scienze n 285 maggio ’92). È stata censita un’area che copre il 10% della sfera celeste, per una profondità di 2 miliardi di anni luce (circa 610 Mpc), individuando circa 2 milioni di galassie. Tenendo conto che una sfera di tale raggio occupa un volume di circa 109 Mpc3 e che il conteggio ha interessato il 10% di tale volume (108 Mpc3), la densità media di galassie nell’universo risulta di 2 galassie per 100 Megaparsec cubici
 

Attualmente la porzione di universo osservabile (distanza-orizzonte), per un universo euclideo, vale

dove h è un fattore di incertezza sul valore della costante di Hubble. Una sfera di tale raggio ha un volume di circa 1010 Mpc3 il quale dovrebbe dunque contenere circa 108 galassie (ng = VU dg = 1010 10-2 = 108), raggruppate in 105 ammassi, a loro volta riuniti in 104 superammassi, per una massa totale dell’universo osservabile dell’ordine di 1020 M).

 

Moti della terra

 

 Moto di rotazione

La terra ruota attorno al proprio asse in circa 24 ore con un movimento antiorario se osservato dal polo Nord Celeste (proiezione lungo l'asse terrestre del polo Nord terrestre sulla volta celeste). Il movimento avviene cioè da W verso E.

 

Prove del moto di rotazione

Oggi possiamo facilmente verificare direttamente tale rotazione attraverso l'osservazione da un satellite in orbita. In passato sono stati invece effettuati esperimenti per dimostrare indirettamente l'esistenza di tale moto. I più famosi si devono a G.B. Guglielmini (1691) e J.B. Foucault (1851).

Esperienza di Guglielmini

Lasciando ripetutamente cadere un grave dalle torri di Bologna Guglielmini verificò che esso non cadeva lungo la verticale individuata dal filo a piombo, ma sistematicamente spostato verso Est. Se individuiamo con A il punto di partenza del grave in cima alla torre e con B il punto a terra che si trova sulla perpendicolare di A, è facile verificare che se la terra ruota A deve muoversi ad una velocità lineare maggiore di B. Trovandosi infatti ad una maggior distanza dall’asse di rotazione terrestre (DA > DB) la velocità lineare di A (VA = w DA) è maggiore della velocità lineare di B (VB = w DB). In altre parole quando la terra ha effettuato in 24 ore una rotazione completa A deve aver percorso una circonferenza maggiore di B nello stesso tempo (24 ore). Per il principio di inerzia il grave lasciato cadere da A deve conservare anche mentre cade la velocità iniziale che caratterizzava la cima della torre e giungendo a terra si troverà un po' più avanti (nella direzione del moto di rotazione terrestre) di B che ruota più lentamente. Poichè il corpo cade sempre spostato verso Est rispetto alla perpendicolare ciò dimostra che la direzione di rotazione della terra è da Ovest verso Est.

Esperienza di Foucault

Il piano di oscillazione di un pendolo ha la caratteristica di mantenere invariato il suo piano di oscillazione rispetto all'universo (stelle fisse).
Foucault appese un pendolo alla cupola del Pantheon a Parigi e lo fece oscillare in modo che la sua punta tracciasse un solco sulla sabbia disposta sul pavimento dell'edificio. Con il passare del tempo il piano di oscillazione ruotava . Non potendo trattarsi di una effettiva rotazione del piano di oscillazione del pendolo, l'unica spiegazione possibile rimaneva una rotazione della terra intera e quindi del pavimento sul quale il pendolo stava lasciando le sue tracce.
Se l'esperimento venisse condotto ai poli il piano di oscillazione eseguirebbe una apparente rotazione completa di 360° in 24 ore. All'equatore non si avrebbe alcuna rotazione, mentre a latitudini intermedie in 24 ore la rotazione sarebbe minore di 360°, tanto minore quanto minore è la latitudine.
Se la latitudine è pari a , il piano di oscillazione del pendolo compie in 24 ore una rotazione pari a 360° sen , con una velocità angolare di 15 sen gradi all'ora. Per compiere quindi una rotazione completa (giorno pendolare) di 360° impiega

 

Conseguenze del moto di rotazione terrestre

 

Alternarsi del dì e della notte

La rotazione della terra espone evidentemente la sua superficie ad un continuo cambiamento di condizioni di illuminazione rispetto alla luce proveniente dal sole. Poichè la terra ruota da Ovest verso Est, il sole sembra sorgere ad Est, effettuare un movimento apparente di salita lungo un arco di circonferenza sulla volta celeste, per poi ridiscendere e tramontare ad Ovest. Quando il sole raggiunge il punto più alto della sua traiettoria apparente si dice che si trova in culminazione (mezzogiorno solare). Il sole è in culminazione su di un punto della superficie terrestre quando sta transitando esattamente sopra il meridiano passante per il luogo.
Il sole è sufficientemente distante dalla terra da poter considerare i suoi raggi paralleli tra loro. In tal modo la terra risulta costantemente divisa in due parti uguali, una illuminata ed una oscura, da un cerchio massimo detto circolo di illuminazione. In realtà, a differenza della luna, dove la mancanza di atmosfera produce una netta separazione tra ombra e luce, sulla terra il circolo di illuminazione non è netto. I fenomeni di rifrazione e di diffusione della luce solare prodotti dalla presenza dell'atmosfera terrestre, producono una zona di penombra, detta crepuscolo. In altre parole i raggi solari che in assenza di atmosfera sfiorerebbero solamente la superficie terrestre senza colpirla, vengono deviati e vanno ad illuminare parzialmente una piccola porzione della zona in ombra, producendo l'illuminazione tipica dell'alba e del tramonto.

 

Le forze d’inerzia: forza centrifuga e forza di Coriolis

Un osservatore solidale con un sistema in moto accelerato, qual è appunto un sistema in rotazione, non verifica il principio di inerzia, nel senso che sperimenta fenomeni in disaccordo con esso. I sistemi in moto accelerato sono perciò detti sistemi non inerziali. In essi, corpi apparentemente non soggetti a forze, manifestano accelerazioni.
In realtà si può dimostrare che la comparsa di tali accelerazioni è legata al particolare sistema di riferimento considerato ed esse non esisterebbero se il sistema fosse fermo o si muovesse di moto rettilineo uniforme. Paradossalmente in un sistema accelerato l'inerzia di un corpo si manifesta come una accelerazione apparente. Per questo motivo tali accelerazioni apparenti vengono attribuite a forze fittizie dette forze d'inerzia.  Le forze d’inerzia, come le accelerazioni ad esse correlate, sono grandezze vettoriali.

Generalità sui corpi in rotazione
Dato un corpo rigido in rotazione attorno ad un asse, tale che, dopo un intervallo di tempo t esso abbia ruotato di un angolo , si definisce velocità angolare istantanea il limite per t 0 del rapporto tra la variazione dell'angolo di rotazione (espresso in radianti) e l'intervallo di tempo t (derivata dello spostamento angolare rispetto al tempo)

Si conviene inoltre di associare a tale grandezza scalare un vettore  del punto P come il prodotto vettoriale

dove a è l'angolo (convesso, minore di 180°) compreso tra i due vettori, cosicché r sin a è la proiezione di r sulla retta perpendicolare che congiunge il punto P all'asse di rotazione e rappresenta dunque la distanza di P dall'asse. Nel caso della terra è facile verificare che, utilizzando il raggio terrestre, la velocità lineare di un punto a latitudine j è pari a

Si rammenti che il prodotto vettoriale ).

 

Forza centrifuga e schiacciamento polare

La più comune forza d'inerzia è la forza centrifuga che si manifesta su corpi ancorati ad un sistema in rotazione. Un osservatore solidale con un riferimento rotante (una giostra ad esempio) si sente spinto verso l'esterno in direzione normale all'asse di rotazione. Tale sensazione è un effetto dell'inerzia che tenderebbe a far muovere l'osservatore di moto rettilineo uniforme rispetto al sistema esterno fisso, lungo la direzione tangente al suo moto rotatorio.
L’effetto più evidente della forza centrifuga è lo schiacciamento delle regioni polari ed il relativo rigonfiamento equatoriale. Il fenomeno si produce infatti per la maggior forza centrifuga cui sono sottoposte le regioni equatoriali rispetto a quelle polari, in virtù di una maggior distanza delle prime dall'asse di rotazione. Si può dimostrare che tale forza è proporzionale ad una accelerazione (accelerazione centrifuga) che vale

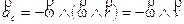
Con v velocità lineare di rotazione del punto. E' facile verificare che l’accelerazione centrifuga è sempre diretta in senso radiale.

Forza di Coriolis e legge di Ferrel

Nel caso il corpo possieda una velocità propria vp rispetto al sistema in rotazione, oltre alla forza centrifuga, compare una seconda forza fittizia, detta forza di Coriolis(1835).
Anche in tal caso si può dimostrare che tale forza è proporzionale ad una accelerazione (accelerazione di Coriolis) che vale

Tale forza fittizia costringe il corpo in movimento a deviare rispetto alla sua direzione iniziale. Gli effetti di tali deviazioni sono particolarmente evidenti per corpi debolmente vincolati alla superficie terrestre, come velivoli.
Le deviazioni prodotte dalla forza di Coriolis sono descritte dalla legge di Ferrel. La  legge di Ferrel (1860 circa) afferma che un corpo in movimento sulla superficie terrestre, subisce una deviazione rispetto alla sua direzione iniziale, verso destra nell'emisfero boreale e verso sinistra nell'emisfero australe. La legge di Ferrel governa il movimento delle masse d'aria (venti) e delle masse d'acqua (correnti marine) costringendole a ruotare in modo caratteristico nei due emisferi.
Per comprendere la legge di Ferrel è necessario aver chiari i seguenti concetti:

• La velocità lineare di rotazione dei diversi punti della superficie terrestre non è costante. I punti più rapidi sono quelli che appartengono all'equatore (essendo quelli più distanti dall'asse di rotazione; V = w D). Man mano che procediamo verso i poli incontriamo paralleli di raggio minore, i cui punti, essendo più vicini all'asse di rotazione, sono sempre più lenti.
• Quando un oggetto si trova su di un punto della superficie terrestre ruota assieme ad essa con la stessa velocità. Nel momento in cui l'oggetto abbandona la superficie terrestre continua per inerzia a mantenere la velocità di rotazione del punto dal quale era partito.

                                      
Immaginiamo ora un aereo che si alzi in volo da un punto A sull'equatore e che proceda lungo un meridiano verso un punto B posto più a Nord. L'aereo si sposta verso punti della superficie terrestre che stanno ruotando verso Est più lentamente di quanto per inerzia non stia facendo lui (VA > VB) . In tal modo L'aereo si trova a precedere in direzione Est i punti della superficie terrestre che sta sorvolando. Ciò equivale ad una deviazione verso destra del velivolo.
Allo stesso modo se l'aereo da A si alza in volo verso un punto C posto sullo stesso meridiano ma in direzione Sud nell'emisfero australe, esso si troverà ad essere più veloce dei punti che sorvola (VA > VC), precedendoli sempre in direzione Est. Ma in questo caso ciò equivale ad una deviazione verso sinistra del velivolo.
Se ora immaginiamo che il velivolo parta da B o da C e si diriga verso il punto A sull'equatore, esso parte da punti aventi una velocità di rotazione verso Est minore del punto di arrivo. Il velivolo trovandosi così a sorvolare punti della superficie terrestre via via più rapidi si trova in ritardo rispetto al moto di rotazione terrestre, spostato cioè in entrambi i casi verso Ovest. Ciò equivale ad una deviazione verso destra nell'emisfero boreale e verso sinistra nell'emisfero australe.
In realtà la forza di Coriolis produce deviazioni laterali solo quando il movimento avviene lungo un meridiano. Si può infatti dimostrare che negli altri casi compaiono anche delle deviazioni verticali (verso l’alto o verso il basso). In particolare se il corpo si muove lungo l’equatore la forza di Coriolis si manifesta unicamente in direzione verticale.

 

                                         
La forza di Coriolis in dettaglio
Per una trattazione più dettagliata e precisa degli effetti della forza di Coriolis è necessario determinare caso per caso la direzione del vettore accelerazione con le regole del prodotto vettoriale.
Possiamo in generale affermare che tale forza si manifesta su tutti i corpi in movimento rispetto alla superficie terrestre, con l'eccezione dei casi in cui i vettori  hanno la stessa direzione (in caso di parallelismo l'angolo compreso tra i vettori è nullo ed essendo sin 0 = 0, anche il prodotto vettoriale si annulla). Casi del genere si hanno quando un corpo si muove lungo la verticale in corrispondenza dei poli (ad esempio un grave che cade sopra un polo) o quando un corpo parte dall'equatore con direzione tangente al meridiano. Quando un corpo si muove rispetto alla superficie terrestre possiamo distinguere due casi:
a) movimento tangenziale (parallelo alla superficie)
b) movimento radiale (perpendicolare alla superficie)

 

1) Movimento tangenziale
Nel caso di un movimento tangenziale è facile verificare che l'angolo a tra i vettori  coincide con l'angolo j di latitudine del corpo. L'accelerazione di Coriolis presenta in tal caso modulo pari a

Per la regola del prodotto vettoriale essa è sempre perpendicolare al piano individuato dai due vettori
Naturalmente se il corpo si muove lungo un parallelo in direzione Ovest la componente orizzontale è diretta sempre verso la sua destra (in questo caso verso il polo nord) mentre la componente verticale è diretta verso il basso. La componente verticale è tanto maggiore quanto più la direzione del vettore velocità si scosta dalla direzione del meridiano passante per il luogo e, a parità di inclinazione, diventa via via maggiore scendendo in latitudine. In particolare un corpo che parta dall'equatore con un qualche angolo rispetto al meridiano presenta solo una componente verticale che diventa massima quando il suo moto è tangente all'equatore.
In definitiva un corpo che si muova verso est subisce oltre ad una deviazione laterale anche una deviazione verso l'alto (e pesa quindi meno di un corpo fermo), mentre un corpo che si muova verso ovest subisce anche una deviazione verso il basso (e pesa quindi di più di un corpo fermo).

 

2) Movimento radiale
Nel caso di un movimento radiale (caduta di un grave, proiettile lanciato verticalmente) è facile verificare che l'angolo a tra i vettori  coincide con la colatitudine, cioè con l'angolo complementare all'angolo di latitudine. Se dunque  =  90 - , l'accelerazione di Coriolis presenta in tal caso modulo pari a

E' semplice verificare che, per la regola del prodotto vettoriale, l'accelerazione di Coriolis è in questo caso sempre tangente al parallelo passante per il luogo e diretta verso est.  Si noti come il parallelo passante per il luogo non è un cerchio massimo e la sua direzione non è quella est-ovest, ma  è deviata verso nord.

 

Durata del moto di rotazione: il giorno

Il tempo impiegato dalla terra per compiere una rotazione intorno al proprio asse è detto giorno. La durata del giorno risulta diversa se si prende come punto di riferimento esterno per misurare la rotazione una stella o il sole.

Essendo molto distante, una stella rappresenta un buon punto di riferimento, potendo essere considerata ferma rispetto alla terra (stella fissa). Il tempo impiegato affinché una stella fissa ritorni in culminazione su di un dato meridiano misura dunque la durata di un'effettiva rotazione di 360° della terra intorno al proprio asse. Il giorno così misurato è detto giorno sidereo e dura circa 23 ore e 56 minuti (23h 56m 4,0989s = 86.164,0989 s).
In realtà il giorno sidereo può ritenersi costante solo in prima approssimazione e per intervalli di tempo sufficientemente piccoli. La terra sta infatti impercettibilmente rallentando. Le stime più recenti forniscono una variazione della velocità angolare della Terra pari a 4 ore ogni 700 milioni di anni. Si ritiene che il motivo più probabile di tale rallentamento sia da ricercare nell’azione frenante delle maree. La terra starebbe trasferendo momento angolare alla luna, la quale sta aumentando progressivamente la sua distanza al ritmo di 3,7 ± 0,2 m/secolo

Nonostante il giorno sidereo sia una misura relativamente esatta della durata della rotazione terrestre, tutte le attività umane sono regolate sulla posizione del sole e non delle stelle.
Se dunque misuriamo il tempo necessario affinché il sole culmini per due volte consecutive sullo stesso meridiano (intervallo di tempo tra due mezzodì) si ottiene il giorno solare, pari a circa 24 ore.
Il sole non si può però considerare fisso rispetto alla terra, poiché mentre la terra compie una rotazione intorno al proprio asse, essa si sposta contemporaneamente sulla sua orbita di un tratto di circa 1 grado rispetto al sole. (la terra impiega infatti circa 365 giorni a compiere una rivoluzione di 360° intorno al sole con una velocità angolare di circa 1° al giorno. Più precisamente impiega un anno sidereo, pari a  31.558.150 secondi, a compiere una rivoluzione intorno al sole rispetto alle stelle fisse).

Una volta che la terra ha dunque compiuto, dopo 23 ore e 56 minuti, una rotazione completa attorno al suo asse, non trova il sole nuovamente in culminazione, essendosi spostata in senso antiorario rispetto ad esso di circa un grado. Per ritrovare nuovamente il sole in culminazione la terra deve dunque ruotare ancora di un angolo pari al suo spostamento rispetto al sole, compiendo una rotazione complessiva di 361°.
Poichè la terra impiega circa 24 ore per compiere una rotazione di 360° intorno al suo asse, la sua velocità angolare di rotazione sarà di 360°/24h pari 15 gradi all'ora. Per coprire un grado impiegherà quindi un quindicesimo di ora pari a 4 minuti circa (235,90s = 3m 55,9s).

 

Composizione dei moti orbitali
Le velocità angolari seguono delle regole di composizione identiche a quelle utilizzate per comporre le velocità lineari.
Si pensi ad esempio ad un’autovettura A che si muova a 50 km/h verso un’autovettura B, la quale si avvicini a sua volta a 30 Km/h. Il risultato è il medesimo se si considera una delle due autovetture ferme e l’altra con una velocità pari a (50 - (-30) = 80 Km/h. Nel caso in cui l’autovettura B si stia allontanando nella stessa direzione di A, la sua velocità relativa risulta pari a (50 - 30 = 20 km/h). Si noti come i valori delle velocità abbiano segno concorde se il loro verso è il medesimo, discorde se il verso è contrario. In modo analogo possiamo comporre i moti orbitali.
Se wrot e wriv sono rispettivamente la velocità di rotazione e di rivoluzione della terra rispetto alle stelle fisse, allora la velocità di rotazione della terra rispetto al sole può ottenersi componendo i due movimenti e sarà pari a (wrot - wriv). Essendo entrambi i moti diretti (antiorari) il loro segno sarà concorde.

da cui si ricava che il giorno solare dura

86400 - 86164,0905 = 235,9095 s = 3m 55,91s più del giorno sidereo

In realtà il giorno solare non ha sempre la stessa durata costante di 24 ore. Essa varia infatti con periodicità nel corso dell’anno a causa dell’eccentricità e dell’inclinazione (o obliquità) dell’orbita terrestre. Il valore di 24 ore che noi utilizziamo rappresenta il giorno solare medio, media dei 365 giorni solari.

Effetto dell’eccentricità
Per la seconda legge di Keplero in perielio la Terra si muove più velocemente intorno al sole e quindi in 24 ore si sposta rispetto ad esso di un tratto leggermente superiore di 1°. La velocità di rotazione terrestre è invece costante e per compiere un po' più di 1° di rotazione al fine di riavere il sole in culminazione impiegherà un po' più di 4 minuti. Il giorno solare in perielio è un po' più lungo di 24 ore. Per ragioni opposte il giorno solare in afelio raggiunge la sua durata minima, inferiore alle 24 ore.

Per effetto della diversa velocità orbitale della Terra, il giorno solare vero in perielio dura circa 8,1 s più del giorno solare medio, mentre in afelio dura  circa 7,7 s meno del giorno solare medio

La durata del giorno solare varia dunque, per effetto della diversa velocità orbitale della Terra, di circa 15,8 secondi nel corso dell’anno, valore che rappresenta la massima escursione nella durata del giorno solare causata dall'eccentricità dell'orbita terrestre.
Gli scarti però si accumulano nel corso dei giorni, e dunque per sapere quanto tempo ritarda o anticipa il Sole vero rispetto al Sole medio in un certo giorno, occorre tenere conto di tutti gli scarti precedenti. Questo porta ad una differenza massima tra giorno vero e giorno medio di circa ± 8 minuti.
Effetto dell’inclinazione (obliquità) dell’orbita
Come abbiamo già detto, dopo un giorno sidereo la Terra si è spostata di circa un grado lungo la sua orbita intorno al Sole e dunque dovrà coprire quest’angolo con un ulteriore rotazione. Possiamo descrivere lo stesso fenomeno pensando che la Terra sia ferma e che il Sole si muova lungo l’eclittica.

L'asse di rotazione della Terra è inclinato sul piano dell'eclittica e così anche l'orbita apparente del sole. Il piano dell'eclittica è inclinato rispetto all'equatore celeste di ε = 23,44°. La proiezione della posizione del Sole sull'equatore celeste introduce un'altra variazione periodica sulla durata effettiva del giorno solare.

Quando il Sole attraversa l’equatore in corrispondenza dei punti equinoziali la sua proiezione sull’equatore si muove più lentamente di quanto non faccia il Sole medio ed il giorno solare vero risulta più breve del giorno solare medio. Quando invece si trova in corrispondenza dei punti solstiziali, il Sole si muove parallelamente all’equatore, la sua proiezione sull’equatore si muove più rapidamente di quanto non faccia il Sole medio ed il giorno solare vero risulta più lungo del giorno solare medio.

Per rendercene conto immaginiamo che il Sole si trovi nel punto gamma (equinozio di primavera) e che sia in culminazione (mezzogiorno) sul meridiano A. Dopo un giorno sidereo la Terra ha compiuto una rotazione di 360° rispetto alle stelle fisse, ma il meridiano A non ritrova il Sole in culminazione, perché il Sole si è spostato lungo l’eclittica di circa 1°. Poiché tuttavia l’eclittica è inclinata di 23,44° rispetto all’equatore, il sole non si è spostato di 1° in longitudine, ma di 1° cos(23,44°)= 0,9175°. Sarà quindi sufficiente che la Terra ruoti di 0,9175° per ritrovare il Sole in culminazione, impiegandoci dunque non 235,90 s, ma 235,90 x cos(23,44°) = 216,43 s.
Il valore 235,90 s (differenza tra il giorno solare medio ed il giorno sidereo) rappresenta dunque il tempo medio tra il tempo minimo impiegato in corrispondenza dei punti equinoziali ed il tempo massimo impiegato nei punti solstiziali pari a 235,90 / cos(23,44°) = 257,12 s

La durata del giorno solare varia dunque, per effetto della obliquità dell’orbita terrestre, di 257,12  – 216,43 = 40,69  secondi nel corso dell’anno..
Anche in questo caso gli scarti però si accumulano nel corso dei giorni, e dunque per sapere quanto tempo ritarda o anticipa il Sole vero rispetto al Sole medio in un certo giorno, occorre tenere conto di tutti gli scarti precedenti. Questo porta ad una differenza massima tra giorno vero e giorno medio di circa ± 10 minuti.

Equazione del tempo
Per ottenere la durata reale del giorno (giorno vero) è necessario sommare gli effetti dell’eccentricità e dell’obliquità. Le due componenti con periodi di un anno e di 6 mesi sono sfasate perchè la posizione del perigeo non coincide ne’ con un equinozio, ne’ con un solstizio.
Sommando i due effetti senza tener conto degli effetti cumulativi si ottiene

Osserviamo che il giorno solare più corto è il 14 Settembre (circa 22 secondi in meno del giorno solare medio), mentre il giorno più lungo è il 21 dicembre (circa 28 secondi in più del giorno solare medio). Sono differenze piccole, che  però si accumulano nel corso dell'anno raggiungendo anche parecchi minuti prima  di cambiare segno.
Tenendo invece conto degli effetti cumulativi si ottiene

 

Osserviamo che il giorno solare vero più lungo cade il 44mo giorno dell’anno (13 febbraio) e quello più corto cade il 304mo giorno dell’anno (31 ottobre). Inoltre il giorno vero dura esattamente 24 ore come il giorno solare medio 4 volte all’anno
giorno 106 (16 aprile)
giorno 164 (13 giugno)
giorno 243 (31 agosto)
giorno 358 (24 dicembre)

 

moto di rivoluzione

La terra possiede un moto di rivoluzione intorno al sole con movimento antiorario per un osservatore posto al polo nord celeste, che compie in circa 365 giorni e 6 ore. Il piano individuato dall'orbita terrestre è detto eclittica.  L'asse di rotazione terrestre è inclinato di 66° 33' rispetto all'eclittica e di 23° e 27' (il valore esatto è 23° 26’ 21,4”) rispetto alla perpendicolare all'eclittica.
Durante il suo moto di rivoluzione intorno al sole l'asse terrestre può essere considerato, in prima approssimazione, fermo o, per meglio dire, esso si muove intorno al sole mantenendo inalterata la sua orientazione rispetto alle stelle fisse (si usa dire che durante il moto di rivoluzione l’asse terrestre rimane sempre parallelo a se stesso).

 

Prove del moto di rivoluzione

 

Parallasse annua

Come abbiamo già visto, le stelle più vicine alla terra sembrano oscillare rispetto a quelle più distanti (considerate fisse) a causa della diversa posizione di osservazione che la terra assume durante il suo moto di rivoluzione. L’angolo di oscillazione è tanto minore quanto più distanti sono gli astri osservati.

Diversa durata del giorno solare

Abbiamo già visto come il giorno solare abbia una lunghezza diversa come conseguenza della differente velocità di rivoluzione della terra lungo la sua orbita. Tale fenomeno può dunque essere portato come prova del moto di rivoluzione terrestre.

Aberrazione delle stelle fisse

Fenomeno scoperto da J. Bradley nel 1728 per il quale tutte le stelle, indipendentemente dalla loro distanza, vengono osservate in una posizione diversa da quella effettiva a causa del moto di rivoluzione della terra. Il fenomeno può essere in prima approssimazione spiegato (come fece lo stesso Bradley) nell’ambito della meccanica classica, supponendo che la velocità della luce si componga vettorialmente con la velocità della terra (la relatività speciale ha in realtà dimostrato che la velocità della luce è una costante di natura e non può comporsi con altri moti relativi). Così facendo si trova che tutte le stelle oscillano intorno alla loro posizione vera di ± 20,5 secondi di grado, quantità definita angolo di aberrazione.

Angolo di aberrazione
Supponiamo che una stella si trovi in S e che la linea visuale che congiunge  S alla Terra in T formi un angolo q con il vettore v, velocità orbitale della terra.  Il risultato è ovviamente il medesimo se pensiamo la terra ferma e la stella soggetta ad un vettore controverso -v. Tale vettore può essere scomposto in una componente radiale (v cosq), che non modifica la posizione della stella, e in una componente trasversale (v sinq) che modifica le coordinate celesti della stella. Infatti tale componente trasversale, componendosi con il vettore velocità della luce c, produce un vettore risultante c’. In tal modo la luce della stella sembra provenire da un direzione diversa e la sua posizione apparente sulla sfera celeste viene ad essere S’. con una variazione di un angolo a delle coordinate celesti effettive.
L’angolo a che la direzione vera forma con la direzione apparente, detto angolo di aberrazione, è tale che

Prendiamo ora in considerazione una stella la cui direzione formi un angolo j con il piano dell’eclittica (j = latitudine eclitticale della stella). Possiamo facilmente osservare come la componente trasversale assuma i valori massimi in A e B, dove q = 90° (± v sin90° = ± v) ed i valori minimi in C e D, dove q = j  (± v sinj).
Se ne deduce che ogni stella presenta sempre lo stesso angolo massimo di aberrazione (per q = 90°), detto costante di aberrazione, che vale

Poiché la velocità media di rivoluzione della terra è v = 29,785 km/s e la velocità della luce è c = 299.792,458 km/s, la costante di aberrazione vale a = 20,5” (l’IAU Unione Astrofisica Internazionale fornisce per l’anno 2000 il valore a = 20,495520” ± 1 10-6”).  La velocità media di rivoluzione si può calcolare assumendo l’orbita terrestre come circolare, con raggio pari alla distanza media Terra-Sole (R = 1 UA, pari al semiasse maggiore a = 1,4959787 108 km) ed il periodo di rivoluzione P pari ad 1 anno sidereo (31.558.150 s)

oppure utilizzando la 3^ legge di Keplero  ed esprimendo il periodo in funzione della velocità media (relazione precedente) si ottiene

In definitiva ogni stella presenta un’oscillazione annua massima di circa 41” (± 20,5”) intorno alla sua posizione vera (il vettore v si orienta infatti in senso opposto ogni 6 mesi) ed una oscillazione minima, orientata perpendicolarmente a quella massima, il cui valore dipende ovviamente dalla latitudine eclitticale j. Se dunque a = 20,5” è la costante di aberrazione e j è la latitudine eclitticale, ogni stella descrive nel periodo di un anno un’ellisse (ellisse di aberrazione) di semiassi a e a sinj. Per le stelle che giacciono sul piano dell’eclittica l’ellisse degenera in un segmento di ampiezza 2a, mentre per le stelle perpendicolari al piano dell’eclittica l’ellisse diventa una circonferenza di raggio a.

 

Conseguenze del moto di rivoluzione: alternarsi delle stagioni

Il fatto che sui due emisferi terrestri (boreale e australe) si alternino diverse stagioni meteorologiche è una delle conseguenze principali del moto di rivoluzione della terra. In realtà il moto di rivoluzione non è l'unico responsabile di tale fenomeno. Ad esso contribuisce anche  la particolare inclinazione dell'asse terrestre ed il fatto che l'asse mantiene inalterata la sua orientazione rispetto alle stelle fisse.
Se infatti l'asse fosse perpendicolare all'eclittica e non inclinato i due emisferi verrebbero raggiunti per tutti i 365 giorni dell'anno dalla stessa quantità di radiazione solare e sarebbero caratterizzati da un'unica stagione uniforme.
Il moto di rivoluzione fa si che l'asse terrestre formi con la direzione dei raggi solari angoli diversi man mano che la terra procede lungo il suo cammino intorno al sole. In tal modo i raggi solari giungono con inclinazione diversa sui due emisferi nei vari periodi dell'anno creando le condizioni per il prodursi di diverse condizioni climatiche. Per descrivere il fenomeno con maggior dettaglio possiamo individuare 4 punti fondamentali dell'orbita in relazione agli angoli formati dall'asse con la direzione dei raggi solari.

 

• punto in cui è minima l'inclinazione dell'asse rispetto ai raggi solari (66° 33'). L’emisfero boreale e più esposto alla radiazione solare.
• punto in cui è massima l'inclinazione dell'asse rispetto ai raggi solari (113° 27' = 90° + 23° 27'). L'emisfero australe è più esposto alla radiazione solare.
• e D) punti intermedi in cui i raggi solari risultano a 90° rispetto all'asse terrestre. I due emisferi risultano egualmente esposti ai raggi solari.

       
Esaminiamo ora in dettaglio le condizioni di illuminazione dei due emisferi nei quattro punti precedentemente individuati.

A) SOLSTIZIO D'ESTATE
La terra raggiunge tale punto poco prima di giungere in afelio. L'afelio viene raggiunto il 4 luglio, mentre il punto di minima inclinazione dell'asse rispetto ai raggi solari viene raggiunto il 21 giugno, detto solstizio d'estate.

La data del solstizio di giugno in realtà oscilla tra il 20 ed il 22 giugno e quella dell’afelio tra il 4 ed il 5 luglio a causa del meccanismo del calendario, che alterna anni civili di 365 giorni ad anni di 366.

Durante il solstizio d'estate i raggi solari risultano perpendicolari (sono allo zenit), a mezzogiorno, sul parallelo di 23° e 27' di latitudine nord. Tale parallelo è detto tropico del Cancro. I raggi solari risultano inoltre tangenti ai due paralleli che si trovano a 66° e 33' di latitudine Nord e Sud, detti rispettivamente Circolo polare artico e antartico.
Durante il solstizio d'estate tutti i punti a Nord del circolo polare artico (calotta polare artica) rimangono illuminati dal sole per 24 ore, mentre tutti i punti a Sud del circolo polare antartico (calotta polare antartica) rimangono al buio per 24 ore.
Il circolo di illuminazione individua un piano inclinato di 23° e 27' rispetto all'asse terrestre e taglia in parti diseguali tutti i paralleli che vanno dall'equatore ai due circoli tranne l'equatore, che viene diviso in due parti uguali. Nell'emisfero boreale sarà maggiore il tratto di parallelo illuminato rispetto a quello oscuro, mentre il contrario avverrà nell'emisfero australe. Ciò comporta che la durata del dì sarà maggiore rispetto a quella della notte nell'emisfero boreale, minore in quello australe, eguale all'equatore.

Poichè i paralleli sono tagliati dal circolo di illuminazione in parti tanto più disuguali quanto più ci avviciniamo ai circoli polari, la differenza di durata tra il giorno e la notte si farà tanto più accentuata quanto più ci sposteremo verso i poli.

In tale situazione si verifica un periodo caldo nell'emisfero boreale (estate boreale) ed un periodo freddo nell'emisfero australe (inverno australe).
Riassumendo l'estate è dunque legata al fatto che il polo nord in questo periodo è inclinato verso il sole ed i raggi solari risultano perciò maggiormente concentrati nell'emisfero boreale (a mezzogiorno il sole risulta più alto sull'orizzonte rispetto a quanto accade d'inverno). Inoltre quanto più un raggio solare giunge inclinato sulla superficie terrestre tanto minore sarà la quantità di energia ceduta per unità di superficie, sia perché si diluisce su di una superficie maggiore, sia perché deve attraversare un tratto più spesso di atmosfera.
Inoltre l'emisfero boreale risulta riscaldato dal sole per un numero di ore più elevato rispetto all'emisfero australe (il dì è più lungo).

 

B) SOLSTIZIO D'INVERNO
Quando dopo circa 6 mesi la terra si trova in prossimità del perielio (che raggiunge il 3 gennaio), l'asse terrestre, essendosi mantenuto parallelo si trova avere la massima inclinazione (113° e 27') rispetto ai raggi solari. E' il polo sud questa volta a puntare verso il sole. La terra si trova in solstizio d'inverno (22 dicembre).
A causa del meccanismo del calendario, anche la data del solstizio di dicembre  oscilla tra il 20 ed il 22 dicembre, mentre quella del perielio tra il 3 ed il 4 gennaio.

I raggi del sole sono perpendicolari al tropico del Capricorno (23°27' di latitudine Sud) e nuovamente tangenti ai circoli polari. Le condizioni di illuminazione risultano essere perfettamente capovolte rispetto al solstizio d'estate. Nell'emisfero Nord si produce una stagione fredda (inverno boreale), mentre nell'emisfero Sud una calda (estate australe).Poichè l'estate boreale cade in afelio essa è leggermente più lunga e meno calda dell'estate australe (la terra è infatti più distante dal sole e si muove più lentamente).L'inverno boreale, cadendo invece in prossimità del perielio , è leggermente più tiepido e più corto di quello australe.Il fatto che l'inverno e l'estate cadano attualmente in prossimità dell'afelio e del perielio è assolutamente casuale. Le posizioni dei solstizi ( e degli equinozi) sono infatti destinate a mutare gradualmente e con regolarità rispetto all'orbita terrestre. Il solstizio d’estate coincideva con l’afelio intorno al  1250 d.C. (coincidenza apsidi - solstizi), mentre gli equinozi verranno a coincidere con gli apsidi (equinozio di primavera in perielio) verso il 6500 d.C.

C - D  EQUINOZI
Gli equinozi occupano una posizione intermedia tra i punti solstiziali, tale per cui i raggi solari risultano perpendicolari all'asse terrestre e giungono quindi (a mezzogiorno) perpendicolarmente all'equatore. Il calore solare viene ad essere quindi egualmente distribuito sui due emisferi. Il circolo di illuminazione coincide con i meridiani, passa per i poli e taglia tutti i paralleli in due parti uguali. Il dì dura 12 ore, come la notte. L’equinozio di primavera viene raggiunto il 21 marzo (19/21), mentre L’equinozio di autunno il 23 settembre (22/24). La linea degli equinozi risulta pertanto perpendicolare all’asse terrestre.
Naturalmente mentre la terra si muove lungo la sua orbita anche l'inclinazione dei raggi solari rispetto al suo asse e quindi alla sua superficie si modifica con regolarità. Il sole che a mezzogiorno si trova allo Zenit al tropico del Cancro durante il solstizio d'estate, con il passare dei giorni si troverà allo Zenit (sempre a mezzogiorno) su paralleli di latitudine via via inferiore, fino a raggiungere l'equatore durante l'equinozio d'autunno, per poi scendere fino al tropico del Capricorno sul quale giungerà allo Zenit durante il solstizio d'inverno.
Qui sembrerà fermarsi per riprendere il suo moto in senso contrario. Il fatto che ai due tropici il sole dia l'impressione di fermarsi per poi tornare indietro ha dato il nome ai solstizi (sol stare). Il nome degli equinozi deriva invece dal fatto che quando il sole si trova allo zenit all'equatore il dì e la notte hanno la stessa durata (aequus nox).

Risulta evidente che il sole non potrà mai trovarsi allo zenit al di fuori delle latitudini comprese tra i due tropici. Ciò dipende dall'inclinazione attuale dell'asse terrestre. Se l'asse fosse ad esempio inclinato di 30° rispetto alla perpendicolare all'eclittica, allora anche i tropici verrebbero a trovarsi a 30° di latitudine nord e sud, mentre i circoli si abbasserebbero a 60° N e S.

I due tropici ed i due circoli polari suddividono la terra in cinque zone dette zone astronomiche o climatiche. La zona compresa tra i due tropici ( l'unica zona della terra dove il sole giunge allo zenit a mezzogiorno per due volte all'anno) è detta zona torrida. Tra i tropici ed i circoli vi sono le due zone temperate (australe e boreale). Al di sopra dei circoli vi sono le due calotte: calotta polare artica e antartica.

 

 Moto doppio conico dell'asse e precessione degli equinozi

Come si è visto, durante il moto di rivoluzione, l'asse di rotazione tende a mantenere inalterata la sua orientazione. Ciò è dovuto al fatto che la terra gira attorno al proprio asse e, come tutti i giroscopi (trottole), si oppone ad ogni sollecitazione che tenda a modificarne l'assetto di rotazione (il momento angolare è una quantità vettoriale e si mantiene costante in modulo, direzione e verso). La luna, il sole ed i pianeti esercitano però sulla terra un'attrazione gravitazionale che risulta maggiore sul rigonfiamento equatoriale, dove è presente un eccesso di massa, rispetto ai poli. Tale attrazione tenderebbe a raddrizzare l'asse portandolo a 90° rispetto al piano dell'eclittica. Il risultato di tali forze su di un sistema rotante, qual è la terra, è quello  di produrre una rotazione dell'asse il quale, facendo perno sul centro della terra, descrive due coni aventi vertice al centro della terra.

Poiché l’equatore celeste è perpendicolare all’asse terrestre, anch’esso esegue il medesimo movimento, cambiando lentamente l’orientazione rispetto alle stelle fisse. Anche la linea degli equinozi, che essendo l’intersezione dell’equatore celeste con il piano dell’eclittica risulta essere sempre perpendicolare all’asse terrestre, ruota rispetto alle stelle fisse con la stessa velocità dell’asse terrestre. Tale rotazione oraria della linea degli equinozi è nota come precessione degli equinozi. La precessione si completa in un periodo di circa 26.000 anni, detto anno platonico.

 

Conseguenze della precessione

• I punti equinoziali stanno lentamente scivolando in senso orario sull’eclittica attraverso le costellazioni zodiacali. Tenendo conto che una costellazione dello zodiaco ha un’ampiezza di 30°, gli equinozi (ed i solstizi) percorrono ciascuna costellazione in 1/12 di anno platonico, pari  a circa 2.150 anni. Se l’equinozio di primavera cadeva 2000 anni fa nella costellazione dell’Ariete, oggi cade nei Pesci. Ma in generale tutti i segni zodiacali sono slittati rispetto alle posizioni che avevano quando è nata l’astrologia (senza che gli astrologi abbiano mostrato di accorgersene).
• Tra 13.000 anni circa l’asse terrestre, avrà compiuto mezzo giro e non punterà più verso la stella polare, ma verso Vega nella costellazione della Lira, che dista ben 47° dalla polare.
• I punti equinoziali (e quindi le stagioni) cambiano la loro posizione rispetto all’orbita terrestre. Attualmente gli equinozi si trovano circa a metà strada tra afelio e perielio (apsidi), ma lentamente li raggiungeranno. Questo terzo punto verrà ripreso in seguito, dopo che avremo discusso dei movimenti dell’eclittica rispetto alle stelle fisse (moti millenari).

Durata del periodo di rivoluzione: l'anno

Viene definito anno il tempo necessario affinché la terra completi il suo moto di rivoluzione intorno al sole. Anche in questo caso la durata dell'anno dipende dal punto di riferimento considerato.
Rispetto ad una stella fissa noi misuriamo l'anno sidereo. Esso misura una effettiva rivoluzione di 360° intorno al sole ed ha una durata di 365 giorni 6 ore e 9 minuti circa (365d 6h 9m 10s  = 365,25636 giorni solari medi = 31.558.150 s).
Come al solito noi usiamo però misurare il tempo rispetto al sole. Il tempo necessario affinché la terra riassuma la stessa posizione rispetto al sole è detto anno solare o tropico. Esso misura in pratica l'intervallo di tempo tra due equinozi o due solstizi dello stesso segno (ad esempio il tempo necessario affinché la terra ritorni all'equinozio di primavera).
A causa del fenomeno della precessione l'anno tropico risulta circa 20 (20m 25s) minuti più breve dell'anno sidereo e pari a circa 365 giorni 5 ore e 49 minuti (365d 5h 48m 45s  = 365,24219 giorni solari medi = 31.556.925 s).

 

Fonte: http://rodomontano.altervista.org/downloads/Astronomia.zip
sito web: http://rodomontano.altervista.org/
Autore del testo: non indicato nel documento di origine

 

Astronomia appunti parte 2

 

 

Visita la nostra pagina principale

 

Astronomia appunti parte 2

 

Termini d' uso e privacy