Astronomia appunti parte 3

 

 

 

Astronomia appunti parte 3

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

moti minori millenari

Come è stato già anticipato le interferenze gravitazionali degli altri pianeti sulla terra producono altri fenomeni, tra i quali ricordiamo:

 

Movimento di rotazione della linea degli apsidi

l’orbita terrestre è un ellisse e le posizioni assunte dagli altri pianeti rispetto ad essa tendono a modificarne sia l'eccentricità che l’orientamento rispetto alle stelle fisse. Come conseguenza delle perturbazioni gravitazionali planetarie essa ruota in senso antiorario, facendo perno sul sole, in circa 111.500 anni.
Se l’orbita rimanesse ferma rispetto alle stelle fisse, un punto equinoziale (o solstiziale) la percorrerebbe completamente in circa 26.000 anni. Ma l’orbita terrestre, e con essa la linea degli apsidi, va incontro alla linea degli equinozi e ne abbrevia in questo modo il periodo di rotazione rispetto all’eclittica a circa 21.000 anni. In altre parole gli equinozi (e naturalmente anche i solstizi) impiegano circa 21.000 anni a percorrere tutta l’orbita (ad esempio da perielio a perielio) e come conseguenza le stagioni sono destinate a manifestarsi in punti via via diversi dell’orbita. Avevamo infatti già avuto modo di dire che l’estate boreale cade oggi in prossimità dell’afelio solo casualmente. Essa sta infatti lentamente scivolando in senso orario sull’orbita, come d’altra parte fanno tutte le stagioni.
In prima approssimazione la linea degli equinozi si sovrappone alla linea degli apsidi ogni 21.000 anni circa e le stagioni si ribaltano ogni 10.500 anni. In altre parole dopo 10.500 anni circa l’asse si trova ad aver compiuto mezzo giro rispetto al sole e le condizioni termiche risultano completamente invertite (l'estate boreale si avrà non più in prossimità dell'afelio ma del perielio). Poichè intorno al  1250 d.C. il solstizio d’estate coincideva con l’afelio (coincidenza apsidi - solstizi) e la linea degli equinozi compie un quarto di giro ogni 5.250 anni circa (21.000/4) gli equinozi verranno a coincidere con gli apsidi (equinozio di primavera in perielio) verso il 6500 d.C.

 

 

 

Variazione dell'eccentricità dell'orbita

Attualmente la differenza tra la distanza afelio-sole e la distanza perielio-sole è di circa 5 milioni di chilometri. Tale differenza è una misura dell'eccentricità dell'orbita. Se infatti essa si riducesse a zero l'ellisse si ridurrebbe ad una circonferenza, se aumentasse l'ellisse si farebbe più eccentrica. Tale distanza è destinata a mutare da un minimo di 1 milione di chilometri ad un massimo di 14 milioni di chilometri. Il ciclo (ad esempio dal valore minimo per ritornare al valore minimo) si completa in 92.000 anni.

 

Variazione dell'inclinazione dell'asse

L'asse terrestre varia la sua inclinazione rispetto alla perpendicolare all'eclittica da un minimo di 22° ad un massimo di 24°20' in un periodo di 40.000 anni circa. Naturalmente al variare dell'inclinazione dell'asse deve variare di conseguenza la latitudine di tropici e circoli.

 

Nutazioni

Il movimento doppio conico dell'asse non è regolare, ma si attua con piccole ondulazioni dette nutazioni (Bradley - 1736). Ciascuna nutazione si completa in 18,6 anni ed è dovuta alle perturbazioni gravitazionali prodotte dalla rotazione oraria (retrograda) della linea dei nodi lunari.

La nutazione comporta una modificazione periodica delle coordinate celesti analoga a quella prodotta dall’aberrazione. Anche le date degli equinozi e dei solstizi subiscono delle oscillazioni come conseguenza della nutazione. A volte si fa riferimento ai solstizi e agli equinozi medi, la cui data è più facilmente calcolabile, non essendo influenzata dalla nutazione.

 

moto rispetto al centro galattico

In realtà la terra segue il sole nel suo movimento di rivoluzione intorno al centro galattico con una velocità stimata di circa 250 km/s, per cui la sua orbita assume la forma di una spirale che si avvita intorno al sole.

La Misura del Tempo

 

Il calendario

L'anno tropico non è un multiplo esatto del giorno solare medio e non inizia quindi in alle ore 0 del 1 gennaio, ma alle 5 e 49 minuti del 1 gennaio. Per evitare questo inconveniente è stato introdotto l'anno civile di 365 (o 366) giorni. Naturalmente assieme all'anno civile deve essere introdotto un meccanismo, detto calendario, in grado di recuperare periodicamente le frazioni di giorno non calcolate nell'anno civile, pena il progressivo sfasamento tra anno civile e tempo astronomico.
Uno dei primi calendari utilizzati a questo scopo è il calendario giuliano, introdotto sotto Giulio Cesare nel 45 a.C. Il calendario giuliano prevede un anno civile di 365 giorni ed un recupero delle circa 6 ore non contate ciascun anno, ogni quattro anni con l'introduzione di un anno di 366 giorni. Il giorno in più veniva aggiunto tra il sesto ed il settimo giorno prima di marzo e chiamato bis sextum, da cui bisestile. L’anno giuliano dura quindi mediamente 365,25 giorni solari medi. L'anno tropico non dura però esattamente 365giorni e 6 ore, ma 365 giorni 5 ore e 49 minuti. Il calendario giuliano, recuperando invece 6 ore, contava circa 11 minuti in più all'anno (11m 15s) e ciascun giorno bisestile introdotto portava uno sfasamento di circa 44 minuti rispetto al tempo astronomico.
Verso il 1500 il tempo civile aveva accumulato uno sfasamento di circa 10 giorni rispetto al tempo astronomico. Nel 1582 il calendario venne perciò riformato sotto papa Gregorio XIII. Vennero dapprima soppressi i 10 giorni in più che si erano accumulati (si passò dal 4 ottobre del 1582 al 15 ottobre del 1582) ed il calendario giuliano venne sostituito dal calendario gregoriano,  lo stesso che attualmente utilizziamo.

Poichè si calcola che gli 11 minuti contati in più ogni anno sfasano il calendario giuliano di circa 3 giorni ogni 400 anni, il calendario gregoriano introduce un nuovo meccanismo per eliminare appunto 3 giorni ogni 400 anni. Tale meccanismo prevede che tutti gli anni secolari aventi le prime due cifre divisibili per 4 continuino ad essere bisestili, mentre gli anni secolari con le prime due cifre non divisibili per quattro non siano più bisestili (mentre lo erano nel calendario giuliano.
Così il 1600 fu bisestile, mentre il 1700, il 1800 ed il 1900 videro soppressi il loro giorno bisestile. In tal modo dal 1600 al 1900, in un periodo di 400 anni sono stati soppressi 3 giorni bisestili. Il 2000 sarà nuovamente bisestile. Poiché ogni 400 anni vi sono 303 anni composti di 365 giorni e 97 anni bisestili di 366 giorni, l’anno gregoriano ha una durata di

ed è quindi circa 27 secondi più lungo dell’anno tropico. Poiché il giorno solare medio è formato di 86.400 secondi, il calendario gregoriano produce uno sfasamento rispetto al tempo astronomico di 1 giorno ogni 86.400/27 = 3.200 anni circa.

 

Fusi orari

In una certa località è mezzogiorno quando il sole culmina sul meridiano del luogo, raggiungendo il punto più alto della sua traiettoria apparente. Ora, poiché il moto apparente del sole è da Est ad Ovest, quando il sole è in culminazione su di un punto A della superficie terrestre, non può essere contemporaneamente in culminazione su di un punto B che si trovi su di un altro meridiano rispetto ad A (cioè che abbia una diversa longitudine). In altra parole il sole non può essere ad esempio contemporaneamente in culminazione a Venezia e a Milano. Ne consegue che quando a Venezia è mezzogiorno, a Milano, che si trova più ad ovest, il sole deve ancora giungere in culminazione e mancherà perciò qualche minuto a mezzogiorno. Per evitare l'inconveniente che luoghi diversi (con diversa longitudine) all'interno di uno stesso stato presentino ore differenti, si è convenuto di dividere la superficie terrestre in 24 spicchi aventi dei meridiani come confini ed un'ampiezza longitudinale di 15° l'uno. Tali spicchi sono detti fusi orari e tutte le zone comprese all'interno di uno spicchio hanno convenzionalmente la stessa ora del meridiano passante per il centro del fuso. Ad esempio per l'Italia il meridiano centrale del fuso è quello che passa per Monte Mario nei pressi di Roma. Quando il nostro orologio segna mezzogiorno (ora legale a parte) in realtà è mezzogiorno solare solo sul meridiano centrale. Lì il sole è effettivamente in culminazione, mentre a Venezia, che si trova leggermente più ad est il sole è già stato in culminazione e la sua ora effettiva (solare) è di mezzogiorno e qualche minuto, mentre ad Aosta, per ragioni opposte non è ancora mezzogiorno.
In effetti i confini dei fusi non seguono perfettamente l'andamento dei meridiani, ma vengono opportunamente modificati in modo da seguire i confini politici degli stati. Naturalmente questo non è possibile per stati molto estesi in longitudine come gli Stati Uniti o la Russia, dove si è costretti ad usare più di un fuso. Il primo fuso è convenzionalmente quello in cui il meridiano centrale coincide con il meridiano fondamentale passante per Greenwich. Quando ad esempio il sole è in culminazione si Greenwich in tutto il primo fuso è mezzogiorno, mentre nel secondo fuso ad est di Greenwich sono le 13, nel terzo le 14 e così via.

 

Linea di cambiamento di data

Poniamo ora che a Greenwich siano le 10 del 6 marzo e immaginiamo di muoverci molto velocemente verso Est con un aviogetto. Mentre attraverseremo i fusi verso Est dovremo far avanzare le lancette dell'orologio, spostandole verso le 11, le 12 e così via fino a che, giunti all'antimeridiano di Greenwich (13° fuso) sposteremo le lancette alle 22 del 6 marzo. Proseguendo verso est il viaggiatore raggiungerà il fuso delle 24, il cui meridiano centrale è detto linea di mezzanotte (LM). Attraversandolo il viaggiatore sposterà il suo orologio dalle 24 del 6 marzo alle 1 del 7 marzo. Immaginiamo ora un altro viaggiatore che stia compiendo anch'egli molto velocemente il giro del mondo ma verso Ovest, partendo da Greenwich il 6 marzo ore 10. Mentre attraversa i fusi verso ovest egli dovrà portare indietro le lancette dell'orologio alle 9 di mattina del 6 marzo, alle 8, alle 7 e così via finche, raggiunta la linea di mezzanotte sposterà le lancette dall'una del 6 marzo alle 24 del 5 marzo. Così i due viaggiatori incontrandosi alla linea di mezzanotte provenienti da parti opposte, si troverebbero d'accordo sull'ora ma non sul giorno. Per evitare tale inconveniente il XIII fuso, che contiene l'antimeridiano di Greenwich, viene diviso dal 180° meridiano in due parti aventi stessa ora, ma date diverse. Qualunque sia l'ora sul mezzo spicchio ad ovest dell'antimeridiano, sul mezzo spicchio ad est è la stessa ora del giorno precedente. In definitiva esistono due meridiani in cui le date cambiano in modo opposto: la linea di mezzanotte (la data aumenta verso est) e la linea internazionale di cambiamento di data (LCD, la data diminuisce verso est). In ogni momento la terra è dunque divisa in due zone aventi date diverse (a est della LCD vi è sempre la data inferiore). Naturalmente quando il sole è in culminazione su Greenwich la linea di mezzanotte coincide con la linea di cambiamento di data e tutti i luoghi presentano la stessa data (attraversando contemporaneamente le due linee la data dovrebbe sia aumentare che diminuire e quindi non varia). Per evidenti ragioni di opportunità la LCD passa sempre attraverso l'oceano e nei pochi casi in cui incontrerebbe qualche isola, viene fatta deviare.

 

L’Orientamento

 

Orizzonte e punti cardinali

Orientarsi significa individuare sull'orizzonte i 4 punti cardinali. L'orizzonte è la circonferenza che delimita la porzione visibile all'osservatore della superficie terrestre, separandola dalla volta celeste.
L’orizzonte geometrico dipende dall’altezza h (in metri) dell’osservatore rispetto al suolo. Il raggio dell’orizzonte geometrico (in metri) è approssimativamente pari a .

L’orizzonte sensibile è in realtà leggermente più ampio a causa dei fenomeni di rifrazione della luce che permettono al nostro occhio di ricevere immagini situate anche oltre l’orizzonte geometrico.
L'EST è il punto dell'orizzonte dal quale sembra sorgere il sole nei giorni equinoziali , detto anche oriente o levante. L'OVEST, o occidente o ponente, è il punto dell'orizzonte dove sembra tramontare il sole nei giorni equinoziali. Nei giorni non equinoziali il sole sorge e tramonta leggermente più a Nord durante l'estate boreale e leggermente più a sud durante l'inverno boreale. L'angolo che i raggi del sole formano con il piano equatoriale nei giorni non equinoziali è detto declinazione solare. I valori della declinazione solare per ogni giorno dell'anno (in pratica la latitudine alla quale il sole risulta allo zenit a mezzogiorno) sono riportati negli annuari astronomici. Ponendosi con la destra ad est e la sinistra ad ovest il NORD risulta posto esattamente dinanzi all'osservatore, mentre il SUD si trova alle sue spalle.

 

Orientamento diurno

Per orientarsi si può dunque indicativamente osservare il punto in cui sorge o tramonta il sole. Nell'emisfero boreale è inoltre possibile individuare il sud dalla posizione del sole a mezzodì (naturalmente se ci troviamo tra equatore e tropico del Cancro è necessario che il sole non stia culminando in un punto più a Nord). Per un osservatore posto nell'emisfero australe la posizione del sole in culminazione indica naturalmente il Nord.

 

Orientamento notturno

Di notte ci si può orientare con la stella polare la quale indica il polo Nord celeste con circa 51' di scarto. ( La stella polare è l'ultima stella del timone del piccolo carro, individuabile prolungando l'asse anteriore del grande carro di circa tre volte la sua lunghezza). Nell'emisfero australe è possibile orientarsi individuando la stella s Octantis che indica il Sud con circa 1° di scarto. Essendo però s Octantis poco luminosa si cerca in genere la costellazione Croce del Sud che però dista 30° dal Polo Sud.

 

Declinazione magnetica

Naturalmente ci si può orientare con la bussola, la quale tuttavia non indica il polo Nord geografico, ma il polo Nord magnetico, il quale si trova attualmente a circa 75° N e 100° W in una delle isole Regina Elisabetta (Canada), mentre il polo Sud magnetico si trova a circa 68° S e 140° E circa.
In effetti non si tratta di veri e propri punti, ma di zone di estensione variabile, che mutano la loro posizione con il tempo. Evidentemente solo per un osservatore posto sul meridiano di 100° W (e sul suo antimeridiano) l'ago della bussola indica contemporaneamente il polo nord geografico ed il polo nord magnetico.
In tutti gli altri casi l'ago della bussola punta verso il polo nord magnetico e non verso quello geografico. La direzione individuata dall'ago (che punta verso il Nord magnetico) forma in tal caso con la direzione individuata dal meridiano passante per il luogo (che punta verso il Nord geografico) un angolo detto declinazione magnetica.

La declinazione magnetica può essere occidentale o orientale e varia da luogo a luogo. Conoscendo la declinazione magnetica di una certa località è possibile individuare con esattezza, tramite una bussola, il polo nord geografico.

 

Determinazione delle coordinate geografiche

Latitudine di notte

Durante la notte la latitudine è pari all'angolo che la visuale verso la stella polare forma con il piano dell'orizzonte. In altre parole è possibile calcolare la latitudine di un luogo semplicemente misurando l'altezza della stella polare sul piano dell'orizzonte.                                      
Nello schema la latitudine del punto A è rappresentata dall'angolo a. E' facile osservare che i due angoli b sono uguali in quanto corrispondenti, mentre i due angoli a sono uguali in quanto entrambi complementari di angoli corrispondenti (le due rette parallele sono 2 raggi provenienti dalla stella polare, uno passante per il centro della terra, uno passante per il punto A. La retta incidente coincide con il raggio terrestre passante per A).
E' facile convincersi che più ci spostiamo verso nord (maggior latitudine) più la stella polare ci appare alta sul piano dell'orizzonte, mentre più ci si sposta verso l'equatore più la stella si abbassa sul piano dell'orizzonte (al polo Nord (latitudine 90°) la stella si trova allo zenit, a 90°, mentre all'equatore (latitudine 0°) i suoi raggi giacciono sul piano dell'orizzonte.

 

Latitudine di giorno

Durante le ore diurne, nei giorni equinoziali, la latitudine è pari al complemento a 90° dell'altezza del sole sul piano dell'orizzonte a mezzogiorno. In altre parole una volta misurato durante un giorno equinoziale l'angolo che i raggi solari formano a mezzogiorno con il piano dell'orizzonte è necessario sottrarlo a 90° per ottenere la latitudine del luogo.
Nello schema a rappresenta la latitudine di A, mentre b rappresenta l'altezza del sole sul piano dell'orizzonte. I due angoli a sono uguali perché corrispondenti, mentre i due angoli b sono uguali perché complementari di angoli corrispondenti ( le due rette parallele sono due raggi provenienti dal sole, uno passante per il centro della terra, uno passante per il punto A. La retta incidente coincide con il raggio terrestre passante per A).
Nei giorni non equinoziali è necessario conoscere il valore della declinazione solare del luogo. Il valore dell'angolo di declinazione va aggiunto all'angolo di latitudine precedentemente calcolato in primavera estate, mentre va tolto in autunno inverno. Tale correzione è evidentemente necessaria per riportare il sole in posizione equinoziale.

 

Longitudine

E' possibile calcolare la longitudine possedendo un orologio sincronizzato sull'ora di Greenwich. Ricordando infatti che il sole impiega 1 ora per percorrere 15° di longitudine è possibile tradurre differenze di tempo tra l'ora locale e l'ora di Greenwich in differenze di longitudine.
Ad esempio se il nostro orologio ci informa che a Greenwich sono le 10 e 30 mentre il sole si trova in culminazione sul nostro meridiano, possiamo dedurre che il sole arriverà in culminazione a Greenwich tra un'ora e mezza. Greenwich si troverà quindi ad Ovest del nostro meridiano ad una distanza di 22° 30', distanza che il sole copre appunto in un'ora e mezzo (15° + 7° 30'). La nostra longitudine sarà pertanto 22°30' E. In generale quando l'ora locale è maggiore di quella di Greenwich il luogo si trova ad Est di Greenwich, quando è minore il luogo si trova ad Ovest.

 

La Luna

 

Generalità
La luna possiede una massa pari ad 1/81 circa di quella terrestre (ML = 7,3483 1022 kg) ed una raggio medio di 1738 km. La sua densità è di 3.3 kg/dm3 contro i 5.5 kg/dm3. La forza di gravità è 1/6 di quella terrestre.

l’aspetto fisico

La superficie lunare presenta grandi distese scure chiamate mari (costituite da estese pianure coperte da una polvere soffice che riflette meno la luce solare, detta regolite). I rilievi lunari visti dalla terra si presentano invece più luminosi e sono costituiti da catene montuose e dai bordi rialzati di crateri (alcuni vulcanici, altri da impatto meteorico). Sulla superficie lunare si notano inoltre dei solchi che possono arrivare a parecchie decine di km di lunghezza e a profondità fino a 500 m. La loro origine è incerta (fessure dovute all'antico raffreddamento ed alla relativa contrazione della crosta; canali scavati dalla lava; fratture (faglie) legate ai movimenti successivi della crosta lunare). Sulla luna è assente sia l'acqua che l'atmosfera, poiché la piccola velocità di fuga caratteristica della luna ha permesso a queste molecole di perdersi nello spazio, vincendo la gravità lunare (probabilmente quando la luna era molto più calda e tali molecole possedevano energie cinetiche piuttosto elevate). L'assenza di acqua ed atmosfera ha impedito che la superficie lunare subisse fenomeni erosivi paragonabili a quelli terrestri, in tal modo la crosta lunare conserva praticamente intatto l'aspetto fortemente craterizzato prodottosi miliardi di anni orsono al momento della sua formazione. L'assenza di atmosfera fa inoltre sì che non si abbiano fenomeni crepuscolari (il circolo di illuminazione è netto). L'albedo  (frazione della luce totale riflessa da un corpo) lunare è solo del 7%, contro quella della terra che è del 35%. In altre parole la terra (a causa delle superfici acquee, dei ghiacciai, delle nubi) riflette, per unità di superficie,  una quantità di luce solare incidente cinque volte superiore a quella riflessa dalla luna ed appare dunque dallo spazio molto più brillante.

 

Moto di rotazione

La luna ruota attorno al proprio asse da Ovest ad Est in circa 27 giorni terrestri (un giorno lunare dura 27 giorni terrestri). Il periodo di oscurità e quello di luce sono quindi molto lunghi. Se a ciò si aggiunge l'assenza di atmosfera, di nubi, acqua e copertura vegetale  si comprende come l'escursione termica (differenza di temperatura tra il giorno e la notte) sia molto elevata. La temperatura diurna può infatti raggiungere un centinaio di gradi °C, mentre di notte si può arrivare a 150 °C sotto zero.

 

Sistema Terra-Luna

In prima approssimazione la luna percorre un’orbita ellittica intorno alla terra, in senso antiorario se osservata dal polo nord celeste. La terra occupa naturalmente uno dei due fuochi dell’ellisse. Il punto di minima distanza Terra-Luna è detto perigeo (da centro a centro 356.410 km), mentre il punto di massima distanza prende il nome di apogeo (da centro a centro 406.697 km).
La distanza media è di 384.400 km.

In realtà la massa della Luna non è del tutto trascurabile rispetto alla massa della Terra ed è quindi solo una grossolana approssimazione affermare che la Luna ruota intorno alla Terra. Più correttamente entrambe ruotano intorno ad un baricentro comune che si trova all’interno della Terra, circa 1700 km sotto la sua superficie. Per questo motivo Terra e Luna possono essere considerate un sistema gravitazionale doppio.

 

 

Moto di rivoluzione e fasi lunari

Il piano dell'orbita lunare non coincide perfettamente con il piano dell'orbita terrestre o eclittica (sul quale giace anche il sole), ma è inclinato rispetto ad esso di circa 5° (5° 8’ 43”).
Il moto di rivoluzione lunare fa sì che essa cambi continuamente la sua posizione relativa rispetto al sole ed alla terra. Si individuano usualmente 4 posizioni fondamentali:

a) congiunzione  La luna si trova tra il sole e la terra
b) opposizione    La terra si trova tra la luna ed il sole
c) quadrature     sono le due posizioni intermedie tra congiunzione ed opposizione. Luna terra e sole formano i vertici di un triangolo rettangolo.
Le posizioni di congiunzione ed opposizione prendono il nome di sizigie o sigizie. In effetti tali termini non si riferiscono solo alle posizioni della luna rispetto al sole ed alla terra ma a possibili posizioni reciproche di qualsiasi corpo del sistema planetario rispetto al sole. Naturalmente in ognuna di queste posizioni è possibile osservare la luna diversamente illuminata dal sole. Le diverse condizioni di illuminazione osservabili dalla terra sono dette fasi lunari.

• quando la luna si trova in congiunzione noi osserviamo la metà non illuminata della luna. La fase lunare è detta di luna nuova o novilunio.  Durante il novilunio la luna sorge, culmina e tramonta con il sole.
• quando la luna è in opposizione osserviamo la metà illuminata della luna. La fase lunare è detta di luna piena o plenilunio. Durante il plenilunio la luna sorge quando tramonta il sole, culmina a mezzanotte e tramonta al sorgere del sole.
• quando la luna si trova nelle due quadrature l'emisfero lunare che noi osserviamo risulta per metà illuminato e per metà oscuro. Le due fasi lunari sono dette primo quarto e ultimo quarto.

La porzione della luna non illuminata dal sole dovrebbe risultare perfettamente oscura. In realtà essa è debolmente illuminata dalla luce del sole riflessa dalla terra. Tale debole chiarore è detto luce cinerea. La corretta interpretazione di tale fenomeno si deve a Leonardo da Vinci. Dalla fase di novilunio a quella di plenilunio si ha luna crescente. Nella fase contraria si ha luna calante.

Mese sidereo

La durata del periodo di rivoluzione è ancora una volta diversa a seconda che prendiamo come punto di riferimento una stella fissa o il sole. Il tempo necessario affinché la luna compia una rivoluzione completa di 360° intorno alla terra, ritornando nella stessa posizione rispetto ad una stella fissa è detto mese sidereo. Esso ha una durata di circa 27,32 giorni terrestri (27d 7h 43m 11,5s  = 27,321661 gsm = 2.360.591,5 s) La luna ruota intorno al suo asse impiegando lo stesso tempo che impiega a compiere una rivoluzione intorno alla terra. La conseguenza di tale curiosa coincidenza è che la luna rivolge sempre la stessa faccia alla terra. L’emisfero nascosto della luna si presenta più ricco di crateri di piccole dimensioni, mentre sono praticamente assenti i grandi mari che caratterizzano l’emisfero rivolto verso la terra. Quest’ultimo, a causa dell’attrazione gravitazionale terrestre, risulta inoltre leggermente più protuberante.

 

Mese sinodico e ciclo delle lunazioni (Metone)

Il mese sinodico o lunazione è il tempo necessario affinché la luna raggiunga nuovamente una fase lunare dello stesso segno. Ad esempio l'intervallo di tempo tra due lune piene consecutive. In altre parole il mese sinodico rappresenta il tempo necessario perché la luna raggiunga nuovamente la stessa posizione relativa rispetto al sole ed alla terra. Il mese sinodico dura circa 29,53 giorni terrestri (29d 12h 44m 2,9s = 29,530589 gsm = 2.551.442,9 s, oltre due giorni in più rispetto al mese sidereo. Ciò è dovuto al fatto che mentre la luna compie il suo moto di rivoluzione intorno alla terra, quest'ultima compie un tratto della sua orbita intorno al sole, cambiando perciò la sua posizione rispetto ad esso.
Poichè il mese sinodico dura 29,53 giorni, un anno non contiene un numero intero di lunazioni. In un anno giuliano si possono susseguire 12 lunazioni complete (354,367 gsm) con l'avanzo di circa 11 giorni. Di conseguenza le fasi lunari non si ripetono ogni anno alla stessa data, ma solo ogni 235 lunazioni, corrispondenti a circa 19 anni tropici.
Tale ciclo è detto ciclo aureo o di Metone (astronomo greco del V sec. a.C.)

 

La luna e le maree

A causa del suo moto di rivoluzione intorno alla terra la luna non sorge, culmina e tramonta sempre alla stessa ora tutti i giorni, ma con circa 50 minuti di ritardo ogni giorno. In altre parole la terra completa una rotazione intorno al suo asse rispetto alla luna in 24h e 50m circa (giorno lunare).

La luna è la principale responsabile (assieme al sole) dei fenomeni mareali che interessano l’idrosfera (ma anche l’atmosfera e in misura molto minore la stessa crosta terrestre). Si è già detto che gli effetti mareali sono dovuti alla diversa attrazione gravitazionale cui sono sottoposti punti diversi di uno stesso corpo. L’idrosfera, pensata per semplicità come un guscio sferico di spessore uniforme, si deforma sotto l’azione della luna assumendo la forma di un ellissoide di rotazione (ellissoide di marea) avente l’asse maggiore orientato lungo la direzione Terra-Luna. In tal modo, osservando il sistema Terra-Luna dal polo nord celeste, possiamo individuare 2 zone di alta marea in corrispondenza dei punti in cui la luna è allo zenit e al nadir e due zone di bassa marea nei punti intermedi, dove la luna appare sull’orizzonte, in procinto di sorgere o di tramontare.
L’asse maggiore dell’ellissoide di marea tende a rimanere sempre allineato con la luna, cosicché la Terra compie una rotazione rispetto ad esso in un giorno lunare (24h 50m). In altre parole, basse ed alte maree si alternano ogni quarto di giorno lunare (6h 12,5m).
Le forze che generano le maree si determinano a causa del non perfetto equilibrio esistente tra forze centrifughe e gravitazionali nei vari punti della Terra. Tale equilibrio esiste solo al centro della Terra, ma non alla sua superficie, dove la forza gravitazionale può risultare maggiore (nei punti più vicini alla luna) o minore (nei punti più distanti) rispetto alla forza centrifuga.

L’azione mareale della Luna è circa 2,2 volte più intensa di quella del Sole. Quando la Luna si trova in sizigie gli effetti mareali dei due astri si combinano e le alte maree presentano le massime ampiezze (maree di sizigie), mentre quando la Luna si trova in quadratura l’effetto mareale del Sole indebolisce quello della Luna, senza peraltro annullarlo (maree di quadratura).

Determinazione dell’accelerazione mareale
Terra e Luna si attraggono con una forza pari a , sempre diretta in senso opposto alla direzione della Luna.
Dunque, mentre la forza centrifuga è identica in tutti i punti, la forza gravitazionale esercitata è invece diversa in intensità e in direzione, a causa della differente distanza dal centro della Luna.  Le forze mareali sono la risultante di tali forze applicate e si manifestano evidentemente in tutti i punti in cui tale risultante è diversa da zero e quindi in tutti i punti che non siano il centro della terra, dove la forza gravitazionale è esattamente controbilanciata dalla reazione centrifuga. Se R è il raggio terrestre e d è la distanza tra i baricentri della Terra e della Luna, l’accelerazione gravitazionale nei punti in cui la Luna è allo zenit e al nadir vale

e quindi l’accelerazione mareale in grado di produrre le alte maree

e nell’ipotesi che il raggio terrestre R sia trascurabile rispetto alla distanza d Terra-Luna (R<<d  e  R2<<d2)   Si può dimostrare che nei punti intermedi, di bassa marea, l’accelerazione mareale è, in modulo, esattamente la metà che nei punti di alta marea, mentre la direzione dei vettori è centripeta, essendo orientata verso il centro della Terra. Gli effetti mareali del Sole sono meno intensi di quelli lunari. Per confrontare gli effetti mareali dei due astri, determiniamo il rapporto tra le rispettive accelerazioni mareali

Mese draconico, retrogradazione dei nodi ed eclissi

Essendo l'orbita lunare inclinata di circa 5° (5° 8’ 43”) rispetto all'eclittica, la luna compie metà del suo percorso di rivoluzione sopra il piano dell'eclittica e metà sotto. I due punti di intersezione, in cui la luna attraversa il piano dell'eclittica sono detti nodi e la linea che li congiunge è detta linea dei nodi. La linea dei nodi rappresenta l'intersezione tra il piano dell'eclittica ed il piano dell'orbita lunare.
La linea dei nodi (intersezione del piano dell'orbita lunare con l'eclittica) ruota, in senso opposto al movimento di rivoluzione lunare (e terrestre), compiendo una rotazione completa in senso orario rispetto alle stelle fisse in 18,6 anni (retrogradazione o regressione dei nodi). In altre parole i nodi vanno incontro alla luna, la quale ritorna pertanto ad un nodo dello stesso segno (ad esempio il nodo ascendente) un po' prima di aver  compiuto una rivoluzione completa di 360° rispetto alle stelle fisse.
Ricordando che il tempo necessario per compiere una rivoluzione completa rispetto alle stelle fisse è definita mese sidereo (27,32166 giorni solari medi = 27d 7h 43m 12s), la luna compierà un'orbita rispetto ad un nodo in un tempo inferiore. Tale intervallo di tempo è detto mese draconitico o draconico (27,212220 gsm = 27d 5h 5m 35,8s = 2.351.135,8 s). La rotazione dell’orbita lunare, misurata dalla regressione dei nodi, muta periodicamente l’inclinazione dell’orbita lunare nei confronti del piano equatoriale.  Così l’angolo che il piano dell’orbita lunare forma con il piano equatoriale va da un massimo di 28° 35’ (23° 26’ + 5° 9’), quando orbita lunare ed equatore sono inclinati in senso opposto rispetto all’eclittica (A), ad un minimo (dopo 9,3 anni) di 18° 17’ (23° 26’ - 5° 9’), quando orbita lunare ed equatore sono inclinati nello stesso senso rispetto all’eclittica (B). La Luna può dunque giungere allo zenit solo su regioni comprese tra le latitudini di 28° 35’ N e S (ed in certi anni solo su regioni comprese tra le latitudini di 18° 17’ N e S).
La regressione della linea dei nodi porta periodicamente questi ultimi ad occupare le posizioni di sizigie. Quando ciò avviene si producono le condizioni necessarie al manifestarsi del fenomeno delle eclissi. Infatti quando la Luna si trova contemporaneamente in sizigie e in uno dei due nodi, Luna Sole e Terra si trovano ad essere allineati. Nel caso l'allineamento sia perfetto si parla di eclissi totali, nel caso ciò non avvenga e la luna in sizigie si trovi solo nelle vicinanze di un nodo si possono produrre eclissi parziali.
In realtà l’eclisse è un fenomeno per cui un astro entra nel cono d'ombra di un altro. Sono dunque propriamente eclissi solo quelle di luna, mentre le eclissi di sole sono in effetti occultazioni (per cui un astro passa davanti ad un altro e lo occulta).

 

Eclisse di Luna

Quando la luna si trova in opposizione e in un nodo essa è destinata a scomparire completamente nel cono d'ombra della terra. Naturalmente durante le eclissi di luna, la luna si trova sempre in plenilunio.

Quando la luna attraversa il cono d'ombra l'eclisse è visibile da tutto l'emisfero terrestre notturno. Poiché l’ombra della Terra è quasi 3 volte più grande della Luna, un’eclissi totale di Luna può durare oltre 100 minuti. Affinché si produca un'eclisse di luna è necessario che la luna ed un nodo si trovino contemporaneamente in opposizione. Se la linea dei nodi fosse ferma rispetto alle stelle fisse, i nodi si verrebbero a trovare in opposizione ogni sei mesi (alternativamente il nodo ascendente e discendente) e potrebbero pertanto verificarsi non più di due eclissi lunari all'anno. Poichè la linea dei nodi si muove di moto retrogrado di circa 20° all'anno, i nodi si presentano in opposizione con periodicità leggermente inferiore ai 6 mesi e quindi a volte possono presentarsi le condizioni per eclissi lunari anche tre volte all'anno.

 

Eclisse di Sole (occultazione)

L'eclisse o occultazione solare si produce ogniqualvolta la luna ed un nodo si trovano in congiunzione. La luna è in grado di oscurare il sole in quanto possiede lo stesso diametro apparente della nostra stella.

Nel caso però in cui la luna si trovi in apogeo e la terra in perielio, il diametro apparente del sole risulta maggiore di quello lunare e si producono le cosiddette eclissi anulari, in cui un anello luminoso del disco solare compare dietro al bordo lunare.
Essendo il cono d'ombra della luna molto meno esteso di quello terrestre, le eclissi solari sono visibili sono in una stretta area ampia da 200 a 300 km (zona di totalità) che si sposta da ovest verso est per migliaia di chilometri, attorniata da una vasta zona di penombra. Per un osservatore che si trovi a percorrere il diametro di tale zona oscura l'eclisse può durare fino a 7m 30s.
A differenza delle eclissi lunari, le eclissi solari possono verificarsi ai due passaggi consecutivi della luna in prossimità di un nodo in congiunzione. Per questo motivo si possono avere fino ad un massimo di 5 eclissi di sole all'anno. In un anno si verificano un minimo di due eclissi (entrambe di sole) ed un massimo di 7 (5 di sole e due di luna; eccezionalmente 4 di sole e 3 di luna). Le eclissi solari sono dunque in assoluto più frequenti. Ma relativamente ad un osservatore particolare risultano più frequenti le eclissi di luna in quanto visibili sempre da tutti gli osservatori dell'emisfero notturno.  L'intervallo di tempo medio che separa due eclissi solari totali osservabili da una particolare regione terrestre è di circa 360 anni.

 

Il ciclo delle eclissi (Saros)

Mediamente si verificano da 2 a 7 eclissi all'anno. I Caldei avevano scoperto che le eclissi si ripetevano con la stessa successione ogni 223 lunazioni pari a 18 anni circa (18 anni e 10-12 giorni, a seconda del numero di anni bisestili presenti). Tale intervallo di tempo è noto come ciclo di Saros. In tale periodo si susseguono 71 eclissi, 43 di sole e 28 lunari.

Librazioni

Si è detto che poiché la rotazione e la rivoluzione lunare hanno la stessa durata di circa 27 giorni, la luna rivolge sempre la stessa faccia alla terra. In realtà noi possiamo vedere circa il 59% della superficie lunare. Ciò è dovuto ad oscillazioni periodiche della Luna dette librazioni, descritte per la prima volta da Galileo e da lui definite titubazioni. Le librazioni si distinguono in vere e apparenti.

• Le librazioni vere o fisiche sono dovute all’attrazione che la terra esercita sul rigonfiamento equatoriale della luna e ad irregolarità nel moto di rotazione lunare.
• Le librazioni apparenti o geometriche si possono suddividere in
• librazioni in longitudine - dovute al fatto che mentre il moto di rotazione della luna avviene a velocità costante, in modo regolare ed uniforme, il moto di rivoluzione è più veloce in perigeo e più lento in apogeo. In tal modo noi possiamo scorgere di volta in volta una piccola fetta di superficie lunare normalmente non visibile, alternativamente ad est e ad ovest (± 7,5°). Il risultato è che la luna, vista dalla terra sembra produrre lievi oscillazioni attorno al suo asse, paragonabili a quelle di una testa che dice di no.
• librazioni in latitudine - dovute al fatto che l’asse di rotazione lunare è inclinato di 6° 41’ rispetto alla perpendicolare all’orbita della luna. Poiché l’asse mantiene costante la sua orientazione rispetto alle stelle fisse (come avviene anche per l’asse terrestre), di conseguenza durante il suo moto di rivoluzione la luna ci mostra alternativamente il suo polo nord ed il suo polo sud (± 6,7°). Il risultato è che la luna, vista dalla terra sembra produrre lievi oscillazioni paragonabili a quelle di una testa che dice di si.

 

• librazioni parallattiche o diurne - dovute al fatto che la distanza Terra-Luna non è trascurabile rispetto alle dimensioni della terra. Osservando la luna quando sorge e tramonta e si trova appena sopra l’orizzonte ci poniamo alle due estremità di una base parallattica costituita approssimativamente dal diametro terrestre e ciò ci consente di scorgere ± 1° di superficie lunare.

L'orbita della luna intorno al sole

Per un osservatore esterno al nostro sistema planetario la luna non compie delle ellissi intorno alla terra, ma segue la terra nella sua orbita ellittica intorno al sole, disegnando intorno ad esso una traiettoria appena ondulata (epicicloide). L'orbita lunare possiede la notevole caratteristica di presentare sempre la concavità rivolta verso il sole

 

Ipotesi sull'origine della luna

I campioni lunari prelevati dalle missioni Apollo hanno indicato che la luna si è formata 4,5 miliardi di anni fa, contemporaneamente dunque alla terra ed al resto del sistema solare. L'analisi chimica dei campioni ha inoltre dimostrato che esistono alcune differenze sostanziali rispetto alla terra. La luna possiede infatti una quantità minore di elementi volatili (K, Na, B etc) mentre è particolarmente ricca di sostanze non volatili o refrattarie (Al, Ca, Th, Lantanidi). Tuttavia rocce terrestri e rocce lunari presentano lo stesso rapporto fra l'isotopo leggero dell'ossigeno (16O) e gli isotopi pesanti (17O e 18O). Ciò fa ritenere che si siano formate nella stessa regione del sistema solare, poiché il rapporto tra gli isotopi dell'ossigeno è molto diverso nelle meteoriti, soprattutto in quelle che provengono da regioni lontane del sistema solare. Sulla base di tali risultanze possiamo analizzare le diverse ipotesi che nel tempo sono state avanzate sull'origine del nostro satellite.

 

 Ipotesi della fissione

Proposta inizialmente da George Darwin, figlio di Charles, prevede che dalla terra allo stato primordiale semifluido si sia staccata una porzione di magma, a causa del rapido moto di rotazione. Molti scienziati ritengono infatti che inizialmente la terra avesse un periodo di rotazione estremamente breve dell'ordine di qualche ora. Da allora ad oggi la terra avrebbe rallentato la sua velocità di rotazione, frenata dall'attrazione gravitazionale della luna. Una variante successiva dell'ipotesi della fissione prevede che la terra abbia addirittura aumentato inizialmente la sua velocità di rotazione a causa dello sprofondamento del materiale metallico verso il centro durante il processo di formazione del suo nucleo. L'aumento di velocità avrebbe generato la forza centrifuga necessaria al distacco del materiale destinato a formare il nostro satellite.
L'ipotesi della fissione spiegherebbe perché la luna presenta una densità media inferiore a quella terrestre. Infatti la luna si sarebbe formata da materiale terrestre superficiale, più leggero di quello che occupa gli strati terrestri più profondi.
Ma non è in grado di giustificare:
- l'inclinazione del piano dell'orbita lunare rispetto all'eclittica
- la diversa composizione chimica evidenziata dalle recenti missioni spaziali
- l'attuale valore del momento angolare del sistema Terra-Luna. Infatti se la luna si fosse staccata dalla terra il momento angolare attuale del sistema Terra-Luna dovrebbe essere uguale a quello della terra prima del processo di fissione, ma il momento angolare attuale del sistema Terra-Luna è notevolmente inferiore a quello richiesto dalle teorie della fissione per giustificare il distacco.

 

 Ipotesi della cattura

Secondo tale ipotesi la luna sarebbe un corpo formatosi in un'altra zona del sistema solare e catturato gravitazionalmente mentre passava casualmente accanto alla terra. Tale ipotesi presenta il vantaggio di poter spiegare la diversa inclinazione dell'orbita lunare e la sua diversa composizione chimica, ma si tratta di un'ipotesi altamente improbabile. Un corpo celeste che passasse infatti casualmente vicino alla terra dovrebbe possedere una traiettoria ben precisa per essere catturato. Anche lievi differenze porterebbero ad un impatto o ad una spinta gravitazionale con sorpasso (effetto fionda, simile al cosiddetto “gravity assist” sfruttato dalle sonde interplanetarie).

 Ipotesi dell’accrescimento

Secondo tale ipotesi la luna si sarebbe formata attraverso un processo analogo a quello attraverso il quale si formò il nostro pianeta. In altre parole il materiale meteorico inizialmente presente sull'orbita terrestre si sarebbe condensato a formare un pianeta doppio. In tal caso però la struttura interna e la composizione chimica della luna dovrebbero essere analoghe a quelle terrestri. Tale ipotesi non spiega dunque perché la luna possieda un nucleo metallico così piccolo (o forse addirittura inesistente, vista la sua densità media così ridotta - 3,3) e le sue rocce presentino abbondanze chimiche così diverse.

 

 Ipotesi dell’impatto meteorico

Secondo tale ipotesi (Hartmann e Davis - 1975; R.A. Daly 1946) la luna si sarebbe formata a causa di un impatto della terra con un gigantesco meteorite. L'enorme quantità di detriti scagliati in orbita si sarebbero poi aggregati a formare la luna. Recentemente tale ipotesi sta trovando un certo consenso in quanto permette di giustificare numerosi evidenze osservative che gli altri modelli non sono in grado di spiegare. Possiamo infatti ipotizzare che

• durante l'impatto il nucleo metallico, più pesante, del meteorite si sia fuso con la terra, mentre  solo i materiali più leggeri siano andati a formare i frammenti  dai quali si condensò la luna.
• il meteorite avesse una composizione inizialmente simile a quella terrestre (stessa composizione isotopica dell'ossigeno), ma durante l'impatto l'enorme liberazione di energia abbia consentito solo agli elementi meno volatili di partecipare alla costituzione del nostro satellite.
• l'impatto sia avvenuto non centralmente, ma secondo un angolo tale da imprimere alla terra un moto di rotazione molto rapido, tale da giustificare il suo elevato momento angolare.

 

Appendice 1 – Distanze in Astronomia

 

Tra le grandezze relative ai corpi celesti le distanze sono sicuramente le più difficili da misurare.
Possiamo suddividere i metodi di misura in primari (o diretti) e secondari (o indiretti).
I metodi primari sono quelli che permettono una misurazione diretta della distanza, in genere utilizzando procedure di tipo geometrico o cinematico, e che consentono una successiva taratura dei metodi secondari che su di essi si appoggiano.

Metodi primari

 

Distanze fino a qualche decina di UA (interplanetarie)

Metodi trigonometrici, Periodi di rivoluzione e Radio-echi

 

Metodi trigonometrici: Parallassi diurne e Massima elongazione
Il termine parallasse indica lo spostamento apparente di due punti situati a distanza diversa dall'osservatore quando quest'ultimo si sposta lungo una retta trasversale alla linea di osservazione.
La distanza tra i due punti di osservazione è detta base parallattica. Lo spostamento parallattico sarà tanto più evidente quanto maggiore è la base parallattica e/o quanto più vicino è l'oggetto all'osservatore. L'angolo compreso tra le due visuali è detto angolo parallattico o parallasse.

Per ottenere uno spostamento parallattico di un corpo appartenente al nostro sistema planetario (pianeta, satellite, asteroide etc) rispetto allo sfondo delle stelle fisse è necessaria una base parallattica sufficientemente estesa, ad esempio il diametro terrestre.  Per utilizzare il diametro terrestre come base parallattica è sufficiente eseguire 2 osservazioni a distanza di circa 12 ore, aspettando che la terra compia mezzo giro intorno al suo asse. La metà dell'angolo compreso tra le due visuali è detto parallasse diurna (o orizzontale).
In pratica si registra la posizione del pianeta P al momento in cui sorge e in cui tramonta (quando cioè si trova all’orizzonte), determinando in tal modo l’angolo 2a.

si determina quindi la distanza in funzione del raggio terrestre R. Infatti per le regole della trigonometria deve essere  .
Ad esempio sapendo che la parallasse media della luna è di circa 0,95°, si trova per essa una distanza pari a circa 60 raggi terrestri

Per corpi celesti che orbitano intorno al sole su orbite interne a quella terrestre è possibile determinare la massima distanza angolare (elongazione massima) del corpo rispetto al sole. Quando infatti osserviamo un pianeta interno (Mercurio, Venere) alla sua massima elongazione, la visuale è tangente all’orbita del pianeta e quindi perpendicolare alla direzione Pianeta-Sole.  In queste condizioni, per le regole della trigonometria,  il rapporto tra la distanza Pianeta-Sole (DP) e la distanza Terra-Sole (DT) deve essere pari al seno dell’elongazione massima emax.

Così, ad esempio, sapendo che l’elongazione massima di Venere è circa 46,5°, possiamo determinare la sua distanza dal sole in Unità astronomiche come

Aristarco ed Ipparco: sulle dimensioni e distanze del Sole e della Luna

I primi ad usare metodi parallattici e trigonometrici per la determinazione di distanze cosmiche furono gli antichi Greci.
La prima stima della distanza della Luna si deve ad Aristarco di Samo (III sec. a.C.), famoso soprattutto per la sua ipotesi eliocentrica, in seguito abbandonata in favore del geocentrismo tolemaico.
Nell’unica opera pervenutaci, “Sulle dimensioni e distanze del Sole e della Luna”, Aristarco afferma correttamente che quando la luna ci appare illuminata per metà (dicotomia lunare) essa deve necessariamente trovarsi al vertice dell’angolo retto di un triangolo rettangolo, ai rimanenti vertici del quale si trovano Terra e Sole. Aristarco valuta in 87° (un quadrante (90°) meno un trentesimo di quadrante (3°)) l’angolo a compreso tra le visuali che dalla Terra portano alla Luna e al Sole.

In termini trigonometrici ciò significa che l’angolo b = 3° e che il rapporto tra la distanza Terra-Luna (DL) e la distanza Terra-Sole (DS) è pari al seno di b.

In realtà al tempo di Aristarco non erano ancora disponibili tavole trigonometriche (la trigonometria nasce con Ipparco di Nicea verso la seconda metà del II secolo a.C) ed egli dimostra che il rapporto deve essere compreso tra 1/18 e 1/20. Il risultato è assolutamente corretto dal punto di vista formale, ma il valore dell’angolo a ottenuto da Aristarco è inferiore al valore reale (89° 51’ 10’’) per la evidente difficoltà di misurare un angolo così prossimo ad un angolo retto. Il valore corretto dell’angolo porta ad un rapporto tra le distanza pari a circa 1/390.

Aristarco osserva poi correttamente che Sole e Luna hanno nel nostro cielo dimensioni apparenti uguali (durante un eclisse di Sole il disco lunare si sovrappone perfettamente a quello solare). Da ciò deriva che distanza e dimensione dei due astri devono essere in proporzione. In altre parole, poiché il Sole è circa 19 volte più distante della Luna, allora anche le dimensioni del Sole devono essere 19 volte superiori a quelle della  Luna.
 
Dalle osservazioni di un'eclisse lunare Aristarco trasse inoltre la conclusione che l'ampiezza dell'ombra proiettata dalla Terra nella regione dove essa è attraversata dalla Luna è due volte il diametro della Luna.

In realtà, come successivamente trovò Ipparco, l’ombra alla distanza della Luna è circa 2,5 volte più grande della Luna stessa.

Se indichiamo con RO il raggio dell’ombra e con RL il raggio della Luna è facile verificare come il percorso effettuato dalla Luna per entrare completamente nel cono d’ombra (A → B) è pari a 2RL. Il tempo necessario per effettuare tale percorso è di circa un’ora. Infatti, poiché la Luna impiega circa 30 giorni (29,5 giorni) per completare una rivoluzione di 360° rispetto al sistema Terra-Sole, essa si muove di 360°/30 = 12° al giorno = 0,5° all’ora. In altre parole impiega un’ora per spostarsi di un suo diametro.
La velocità del moto di entrata sarà ovviamente pari a 2RL/1

Il percorso effettuato dalla Luna per attraversare completamente il cono d’ombra rimanendo al suo interno (B → C)  è pari a (2RO - 2RL). Il tempo necessario (tempo di totalità) per effettuare tale percorso è di circa un’ora e mezza.
La velocità di tale moto di entrata sarà ovviamente pari a (2RO - 2RL)/1,5.
Trattandosi di un tratto breve e limitato dell’orbita lunare possiamo assumere come costante la velocità di rivoluzione e scrivere pertanto

2RL/1 =  (2RO - 2RL)/1,5

da cui, riordinando, si ottiene

RO = 2,5RL

Aristarco usa questi dati per calcolare le dimensioni e la distanza della Luna, sfruttando lo schema geometrico che si viene a creare durante un’eclisse di Luna.
Dati
1) RO = 2RL
2)
3) dimensione angolare Sole = dimensione angolare Luna = 0,5°

dalla similitudine dei triangoli BCD e ABE si ricava la proporzione

e, sostituendo opportunamente

Ricordando che Aristarco aveva trovato  DS/DL = 19 ed RS = 19 RL, la proporzione diventa

che, riordinata, fornisce

Per Aristarco dunque le dimensioni lunari sono circa un terzo (20/57 ≈ 1/3) di quelle terrestri.

Si noti come il valore trovato da Aristarco per le dimensioni della Luna è praticamente indipendente dal valore assegnato al rapporto DS/DL = 19. Se ipotizziamo infatti che la distanza del Sole aumenti e dunque il rapporto DS/DL tenda ad infinito, si trova che il rapporto RL/RT tende a 1/3.
Se infatti poniamo DS/DL = RS/RL =  k, la relazione diventa

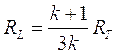
se k tende ad infinito, allora k + 1 ≈ k e la relazione diventa

Poiché, come abbiamo detto, per Aristarco le dimensioni dell’ombra terrestre alla distanza della Luna sono pari a 2 volte le dimensioni della Luna e le dimensioni della Luna sono circa un terzo delle dimensioni terrestri, possiamo scrivere
RO = 2RL = 2 ⅓ RT = ⅔ RT

Per Aristarco l’ombra della Terra si rimpicciolisce di circa un terzo delle dimensioni terrestri o, se vogliamo, si rimpicciolisce di un diametro lunare.

Nella sua opera Aristarco scrisse che il Sole e la Luna presentavano il medesimo diametro apparente di 2° (1/45 di quadrante). Tuttavia Archimede scrisse che Aristarco fu il primo a determinare che il Sole e la Luna presentavano il medesimo diametro apparente di mezzo grado. Se consideriamo corretta l’informazione di Archimede, questo significa che per Aristarco erano necessari 720 diametri lunari (pari a 1440 RL) per completare una circonferenza di 360° sulla sfera celeste avente raggio pari alla distanza Terra-Luna (DL). Quindi l’orbita descritta dalla Luna intorno alla Terra è una circonferenza la cui lunghezza corrisponde a 720 volte il diametro della Luna. Il raggio DL di tale circonferenza si ottiene ovviamente dividendo la sua lunghezza per 2π

Ipparco
Anche Ipparco si occupò del problema. Egli pubblicò i suoi risultati in due libri intitolati Peri megethoon kai 'apostèmátoon ("Sulle Dimensioni e Distanze"). che non ci sono pervenuti, ma del cui contenuto parla Tolomeo nell’Almagesto e Pappo di Alessandria, nel suo commentario all’Almagesto.
Nell’Almagesto Tolomeo attribuisce inoltre ad Ipparco l'invenzione di uno strumento, detto diottra, per misurare i diametri apparenti del Sole e della Luna e Pappo d'Alessandria, nel suo Commento al quinto libro dell'Almagesto, descrive la diottra come una guida scanalata lunga quattro cubiti (circa 2 metri) dove sono montate due pinnule rettangolari. La prima, fissa a un estremo della guida, reca un piccolo foro d'osservazione; la seconda, scorrevole lungo la scanalatura, è priva di fori. Puntato lo strumento, si sposta avanti e indietro la pinnula mobile finché copre esattamente il disco del Sole o della Luna. Il rapporto fra il diametro della pinnula mobile e la sua distanza dalla pinnula fissa permette di calcolare l'angolo sotteso dal corpo celeste.

Utilizzando la diottra, Ipparco trovò che le dimensioni della Luna variano durante il suo moto orbitale, mentre non fu in grado di rilevare nessuna variazione sensibile del diametro apparente del Sole. Egli trovò che alla distanza media della Luna, il Sole e la Luna aveva il medesimo diametro apparente e che il diametro della Luna sta 650 volte nell’intera circonferenza. In altre parole il diametro apparente medio è pari a 360°/650 = 0,554° = 0° 33' 14".
Ipparco notò anche che la Luna presenta una parallasse diurna, risulta cioè spostata dalla sua posizione rispetto al Sole o alle stelle, se osservata da punti diversi della superficie terrestre.
La parallasse diurna della Luna è l’angolo πL sotto il quale un osservatore, posto sulla superficie della Luna, osserverebbe il raggio della Terra.

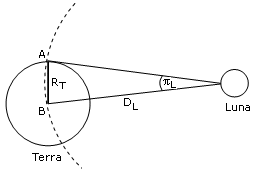
Misurando l’entità di tale angolo di parallasse è dunque possibile calcolare la distanza Terra Luna (DL) espressa in Raggi terrestri. Il raggio Terrestre può essere infatti approssimato all’arco AB posto sulla circonferenza di raggio DL. Il rapporto RT/DL è dunque pari alla parallasse lunare espressa in radianti. E dunque DL, espresso in raggi terrestri, è semplicemente il reciproco della parallasse lunare espressa in radianti.

Per il Sole Ipparco, non fu tuttavia  in grado di individuare alcuna  parallasse osservabile (oggi sappiamo che il suo valore è πS = 8,8", nettamente al di sotto della risoluzione dell’occhio umano che è di circa 1’.
Probabilmente per questo motivo nel primo libro, Ipparco ipotizzò che la parallasse del Sole fosse effettivamente nulla, il che equivale a porre idealmente il Sole a distanza infinita. Come conseguenza di tale ipotesi, la diversa manifestazione di una medesima eclisse di Sole per osservatori posti in punti diversi della superficie terrestre deve essere attribuita solo alla parallasse lunare.

In altre parole, la posizione apparente della Luna nel cielo rispetto al Sole dipende dalla posizione dell’osservatore sulla superficie terrestre. Tale spostamento apparente è detto parallasse lunare e la sua entità dipende dalla distanza che separa i due punti di osservazione e, ovviamente, dalla distanza della Luna.
Ipparco utilizzò probabilmente le informazioni relative all’eclisse di Sole  del 14 marzo 190 a.C, che fu totale per gli osservatori posti nell’Ellesponto (Dardanelli, latitudine φ = 41°), mentre risultò parziale per gli abitanti di Alessandria (latitudine φ = 31°) che videro occultati solo i 4/5 del Sole.

Partendo da questi dati Ipparco concluse che la distanza della Luna doveva essere compresa tra 71 ed 83 raggi terrestri.
Non conosciamo esattamente il procedimento utilizzato da Ipparco per ottenere tale risultato, anche se diversi storici della scienza hanno tentato varie ricostruzioni.

Poiché per Ipparco il Sole occupa sulla sfera celeste 0,554°, la frazione di Sole non oscurata dalla Luna ad Alessandria corrisponde a 1/5 di 0,554° pari a 0,111° . Tale angolo è uguale all’angolo di parallasse a del bordo inferiore C della Luna osservato dai due punti A e B sulla superficie terrestre.
Dunque l’arco AB posto sulla circonferenza di raggio DL ha una lunghezza pari a

L’arco AB posto sulla superficie terrestre, di ampiezza pari alla differenza di latitudine (Δφ = 10°) tra l’Ellesponto ed Alessandria, ha invece una lunghezza pari a

Se ora assumiamo che questi due archi siano approssimativamente uguali possiamo scrivere

da cui

Tale risultato è stato ottenuto ponendo il Sole e la Luna allo zenit tra Ellesponto ed Alessandria, perpendicolare dunque ad una latitudine, intermedia tra 41° e 31°, pari a 36° . Possiamo affinare il risultato se consideriamo che il 14 Marzo la declinazione del Sole è di circa 3° Sud.

La direzione dei raggi solari è dunque inclinata di 36 + 3 = 39° rispetto alla verticale che passa per la latitudine di 36°. In tal modo l’arco di circonferenza BD (approssimato con un segmento) avente raggio DL forma anch’essa un angolo di 39° con l’orizzonte e la sua lunghezza può essere correlata all’arco AB (anch’esso approssimato con un segmento) che congiunge l’Ellesponto ad Alessandria dalla relazione
BD / cos 39° = AB

 

sostituendo nella relazione precedente otterremo

Nel secondo libro Ipparco usa un metodo diverso per la stima delle distanze, utilizzando un eclisse di Luna.

Se consideriamo il triangolo STL, avremo che la somma dei suoi angoli interni è ovviamente pari a 180°
πS + πL + β = 180°
dove
πS = Parallasse diurna del Sole
πL = Parallasse diurna della Luna

Ma anche la somma dei tre angoli a + β + γ = 180° andando a formare un angolo piatto

dove
a = dimensione angolare del Raggio solare
γ = dimensione angolare del raggio dell’ombra terrestre alla distanza della Luna

Dunque possiamo scrivere

πS + πL + β = a + β + γ
ed in definitiva
πS + πL = a + γ

I valori di a e  β erano, come sappiamo, noti ad Ipparco.
Le dimensioni angolari del Sole (uguali a quelle della Luna) erano stati stimati da Ipparco a 0,554° e dunque a = 0,554° / 2 = 0,277°
L’ombra terrestre alla distanza della Luna era stata valutata da Ipparco pari a 2,5 volte le dimensioni della Luna e dunque, essendo il raggio lunare apparente uguale a quello del Sole,  γ = 0,277° x 2,5 = 0,6925°.

In definitiva
a + γ = 0,277° + 0,6925°. = 0,9695°

Se ne deduce che la somma della parallasse diurna del Sole e della Luna deve essere pari a 0,9695° e, noto uno dei due valori, l’altro resta univocamente determinato.

πS + πL = 0,9695°

A differenza di quanto aveva fatto nel primo libro in cui aveva assegnato al Sole una parallasse nulla (πS = 0), nel secondo libro Ipparco assegna al Sole una distanza dalla terra di 490 Raggi terrestri, che corrisponde ad una parallasse solare pari a πS = 0,1169° ≈ 7’

Se infatti DS è la distanza Terra-Sole, la circonferenza avente raggio DS ha una lunghezza 2πDS ed il raggio terrestre RT rappresenta una frazione di tale circonferenza pari a πS/360

e dunque, se DS = 490 RT, la parallasse solare deve valere

 

Assegnata dunque al Sole una parallasse di 0,1169°, resta determinata la parallasse lunare

πL = 0,9695° - πS =  0,9695° - 0,1169° = 0.8526°

valore che ci permette di calcolare la distanza della Luna in raggi terrestri utilizzando la relazione

da cui

Possiamo notare come  per Ipparco il valore della parallasse assegnata al Sole rappresenti un limite superiore, superato il quale, la paralasse solare sarebbe osservabile e misurabile. In altre parole la parallasse solare potrebbe avere qualsiasi valore compreso tra 0° e 0,1169°. Se ora facciamo tendere a zero il valore della parallasse solare osserviamo come la distanza della Luna tenda a 59 raggi terrestri.
Infatti per πS =  0 la parallasse lunare vale
πL = 0,9695° - πS =  0,9695° - 0= 0,9695°
e la distanza della Luna diventa

Periodi di rivoluzione (Terza legge di Keplero)
La terza legge di Keplero afferma che il quadrato del periodo di rivoluzione di un pianeta è direttamente proporzionali al cubo della sua distanza media (semiasse maggiore a dell’orbita ellittica) dal sole.

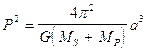
Ovviamente la legge vale per qualsiasi corpo celeste in orbita intorno al sole (ad esempio una cometa). Poichè tutti i corpi celesti in orbita intorno al nostro sole possiedono una massa trascurabile rispetto alla massa solare, possiamo scrivere . Se poi misuriamo il semiasse maggiore a dell’orbita in UA, il periodo P in anni terrestri e le masse in unità solari, la relazione diventa

La misura del tempo di rivoluzione (in anni) di un corpo celeste intorno al sole ci permette dunque di calcolare la sua distanza media dal sole in unità astronomiche. Ad esempio, sapendo che Giove impiega 11,86 anni terrestri a compiere una rivoluzione intorno al sole possiamo determinare la sua distanza che risulta essere pari a

Radio-Echi
E’ possibile determinare la distanza di un corpo celeste inviando sulla sua superficie un fascio di onde elettromagnetiche e misurando il tempo necessario affinché queste vengano riflesse e ritornino sulla terra. Essendo c la velocità della luce e 2t il tempo di andata e ritorno la distanza sarà pari a d = ct.
In realtà, poiché la terra si muove intorno al sole durante il periodo di misurazione, la formula per il calcolo della distanza dovrà tenerne conto e sarà pertanto più complessa.
Affinché la radiazione non venga diffusa e quindi si disperda è necessario utilizzare una lunghezza d’onda più grande delle asperità presenti sulla superficie riflettente. Per i pianeti si usano lunghezze d’onda dell’ordine del metro.

 

 

 

Distanze fino a qualche centinaio di parsec

Parallassi annue e Parallassi di gruppo

Parallassi annue
Eseguendo due osservazioni di una stella relativamente vicina a distanza di 6 mesi, è possibile individuare una sua oscillazione rispetto allo sfondo delle stelle fisse.  In 12 mesi le stelle più vicine sembrano infatti percorrere un ellisse sullo sfondo delle stelle più lontane (fisse). Tale ellisse non è altro che la proiezione dell'orbita della terra sulla sfera celeste. L'angolo 2 sotto il quale noi osserviamo l'asse maggiore di tale ellisse apparente è lo stesso sotto cui un osservatore posto sulla stella osserverebbe l'asse maggiore dell'orbita terrestre. La metà di tale angolo, pari ad , è detto parallasse annua della stella. Tale angolo permette la misura della distanza d della stella (o del pianeta in caso di parallasse diurna). Ricordando infatti che in un triangolo rettangolo il rapporto tra le misure dei cateti è pari alla tangente dell'angolo opposto al primo cateto, potremo scrivere:

Naturalmente lo spostamento apparente e il conseguente valore della parallasse risulterà tanto maggiore quanto più la stella è vicina alla terra, mentre diminuirà, al punto da non essere più misurabile per stelle molto distanti. Quando la parallasse annua di una stella è di 1" (1/3600 di grado), la relazione precedente fornisce una distanza di

Una stella dista quindi 1 parsec dalla terra quando misuriamo per essa un angolo di parallasse di 1 secondo di grado (1"). Nessuna stella, per quanto vicina, presenta una parallasse superiore al secondo di grado. La stella più vicina, Proxima Centauri (cielo australe), presenta una parallasse di 0,76" e quindi dista da noi 3,26/0,76 = 4,3 al.

Le prime determinazioni di una parallasse stellare annua si devono a Struve (1822 - Aquilae 0,181") e a  Bessel (1837 - 31 Cygni 0,314"). Attualmente i nostri strumenti non ci permettono di apprezzare angoli inferiori al centesimo di secondo ed è quindi impossibile determinare la parallasse di stelle la cui distanza sia superiore a 100 parsec (circa 300 al).

Parallassi di gruppo (o di ammasso)
Alcuni gruppi di stelle, gravitazionalmente legate all’interno della nostra galassia, si muovono sulla volta celeste in modo praticamente solidale, presentando quasi il medesimo moto proprio (m in arcsec/anno). Gli esempi più importanti si trovano tra gli ammassi aperti (gli ammassi delle Jadi e delle Pleiadi nel Toro).
Per questi gruppi di stelle è a volte possibile individuare anche il punto della sfera celeste (apice del moto) verso il quale sembrano convergere le singole stelle. Il movimento delle stelle sulla sfera celeste è rappresentato dalla velocità tangenziale (Vt), proiezione della velocità spaziale della stella (Vs) in direzione perpendicolare alla visuale e tangente alla sfera celeste.

Mentre i vettori Vs sono tutti praticamente paralleli tra di loro (tutte le stelle di un gruppo si stanno muovendo insieme nello spazio), è facile verificare che i vettori Vt, essendo tangenti ad un cerchio massimo, devono convergere verso un punto comune (i cerchi massimi si intersecano sempre), detto appunto apice del moto.

Si può dimostrare che l’angolo a compreso tra la visuale Terra-Ammasso e la direzione Terra-Apice è pari all’angolo compreso tra il vettore Velocità spaziale (Vs) ed il vettore Velocità radiale (Vr). Essendo poi , possiamo scrivere

e ricordando che la velocità radiale è legata al red-shift dalla relazione , si avrà

D’altra parte la velocità tangenziale è legata al moto proprio, dalla relazione che lega la velocità lineare alla velocità angolare (V = w R)

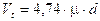
il coefficiente 4,74  è necessario per convertire l’unità di misura del moto proprio da arcsec/anno in rad/s e la distanza d da parsec in km, in modo che la velocità trasversale venga data in km/s.

dove, 206.265 è il numero di secondi di grado contenuti in un radiante (ed anche il numero di unità astronomiche contenute in un parsec) e 31.557.600 è il numero di secondi di tempo contenuti in un anno giuliano di 365,25 giorni. In definitiva si avrà

Eguagliando i due secondi membri ed esplicitando la distanza (espressa in parsec) avremo infine

Il metodo delle parallassi di gruppo permette di stimare distanze fino a qualche centinaio di parsec.
Metodi secondari

L’intervallo di distanza tra i 0,5 kpc (limite delle misurazioni dirette) e i 50 Mpc (limite al di sotto del quale la relazione di Hubble risulta poco affidabile) viene coperto da tutta una serie di metodi secondari che si basano in gran parte su indicatori di distanza.

Indicatori di distanza
Gli indicatori di distanza sono oggetti celesti di luminosità intrinseca L (o magnitudine assoluta M) nota. Vengono anche chiamati candele campione o candele standard.
Le parallassi ottenute tramite indicatori si dividono in due classi in relazione al criterio di calibrazione della funzione di luminosità: parallassi spettroscopiche e parallassi fotometriche. Con le prime si ricava la magnitudine in funzione delle caratteristiche dello spettro, con le seconde si riconosce per certe sue caratteristiche un oggetto celeste di luminosità nota o calcolabile (stelle variabili, novae, supernovae, ammassi globulari, regioni H II etc)
Una volta individuato un indicatore di distanza è sufficiente misurarne la luminosità apparente l (o la magnitudine apparente m) perché sia calcolabile la distanza tramite le note relazioni fotometriche. Ricordando infatti che si avrà

Tenendo presente che attualmente i nostri strumenti sono in grado di percepire oggetti fino ad un limite di luminosità m » 20, è possibile calcolare la massima distanza (in pc) entro la quale un indicatore di magnitudine M può essere individuato e quindi utilizzato, applicando la

Le distanze fino a qualche decina di Kiloparsec: Parallassi spettroscopiche e Parallassi dinamiche

Parallassi spettroscopiche
Il metodo si basa sulla possibilità di riconoscere il tipo spettrale di una stella e la classe di luminosità alla quale appartiene. In genere, noto il tipo spettrale, si risale alla luminosità misurando la larghezza delle righe di assorbimento (sistema MK).

Si è potuto notare che a parità di tipo spettrale le stelle presentano le righe di assorbimento del loro spettro più o meno allargate. Si ritiene che il fenomeno sia dovuto alla diversa pressione esercitata dal plasma che costituisce la stella. Maggiori sono le dimensioni stellari, più il plasma è rarefatto (la sua pressione è bassa) e più le righe spettrali si restringono.Una minor larghezza delle righe spettrali è dunque indice di maggiori dimensioni stellari e quindi, a parità di temperatura, di maggiore luminosità.

 

Parallassi dinamiche
Ad un sistema doppio visuale è possibile applicare la terza legge di Keplero

la quale, se misuriamo il semiasse maggiore a dell’orbita in UA, il periodo P in anni terrestri e le masse in unità solari, diventa

Se p è l’angolo (in secondi d’arco) sotto il quale vediamo il semiasse maggiore dell’orbita del sistema doppio, allora la sua distanza d in parsec si ottiene come

Poiché il periodo di rivoluzione è facilmente determinabile, il metodo può essere utilizzato solo se è possibile assegnare le masse alle due componenti stellari. Si tenga comunque presente che le stelle non presentano un intervallo di masse molto esteso. Inoltre, essendo la somma delle masse sotto radice cubica, un errore nell’assegnazione delle masse non incide in modo sostanziale sul risultato. Se le masse sono completamente sconosciute è possibile, al fine di stimare grossolanamente la distanza,  utilizzare un valore medio che per i sistemi doppi di stelle è .

Le distanze fino a qualche Megaparsec

 

Cefeidi, Regioni H II, Novae, Parallassi nebulari

Le Cefeidi
Sono stati i primi indicatori di distanza, introdotti in astronomia all’inizio del ‘900. Si tratta di stelle variabili in cui il periodo di variabilità è correlato alla magnitudine assoluta. Tra le diverse classi di Cefeidi si possono ricordare le Cefeidi classiche, le RR Lyrae e le W Virginis, che presentano le seguenti relazioni (con P in giorni)

Classiche                                     W Virginis                        RR Lyrae
Essendo il periodo massimo di una cefeide intorno ai 50 gg, la loro magnitudine massima risulta essere pari a circa -6. Esse possono essere pertanto utilizzate come indicatori fino a distanze dell’ordine dei 106 pc.

Le regioni H II
Quando nei bracci delle galassie a spirale si formano stelle molto calde (associazioni O-B), la regione gassosa circostante viene eccitata con formazione di una nebulosa in emissione (regione H II) la cui dimensione (Raggio di Strömgren) e luminosità dipendono dal tipo spettrale (e quindi dalla temperatura) della stella eccitante. Una volta individuato il tipo spettrale della stella eccitante è quindi possibile risalire alle caratteristiche della regione H II. Tali regioni possono essere utilizzate come indicatori di distanza sia utilizzando i valori di magnitudine assoluta, sia utilizzando i valori della loro estensione radiale (misurando la loro dimensione angolare apparente e risalendo alla loro distanza tramite le note relazioni trigonometriche)

Tipo spettrale	Magnitudine visuale	Temperatura Efficace	Raggio di Strömgren (pc)
O5	-5,6	48.000	108
O6	-5,5	40.000	74
O7	-5,4	35.000	56
O8	-5,2	33.500	51
O9	-4,8	32.000	34
O9.5	-4,6	31.000	29
B0	-4,4	30.000	23
B0.5	-4,2	26.200	12

Le Novae
Le novae sono esplosioni stellari che si producono in sistemi doppi. Nel giro di 2-3 giorni la loro luminosità iniziale aumenta fino ad un massimo per poi ritornare lentamente al minimo. La magnitudine assoluta massima raggiunta da una nova può essere stimata ricorrendo alla seguente relazione
M = -11,75 + 2,5 log t
Dove t è il tempo in giorni che la nova impiega a diminuire di 3 gradi la sua magnitudine massima.
Mediamente t » 50 gg e la magnitudine assoluta media di una nova al massimo vale intorno a -7,5. 

 

Parallassi nebulari
Novae e supernovae generano degli involucri gassosi in rapida espansione radiale i quali, essendo eccitati dall’esplosione stellare che li ha generati, producono uno spettro in emissione.
Poiché una parte del gas in espansione si avvicina ed una parte si allontana rispetto all’osservatore ciascuna riga subisce contemporaneamente un red ed un blu-shift che la allarga. L’entità dell’allargamento delle righe permette ovviamente di calcolare la velocità v di espansione dell’involucro. Dopo un tempo t l’involucro gassoso presenterà un raggio R = vt (nell’ipotesi che la velocità sia rimasta costante). Se l’involucro gassoso viene visto dalla terra sotto un angolo 2a, la distanza d sarà pari a

 

Le distanze fino a qualche decina di Megaparsec

 

 

Ammassi globulari e Supergiganti estreme

L’ammasso globulare più luminoso di una galassia
Gli ammassi globulari di una galassia presentano una magnitudine assoluta media intorno a -7, con valori massimi intorno a -10. Ipotizzando quindi che l’ammasso globulare più luminoso di una galassia presenti magnitudine assoluta -10, possiamo stimarne la distanza
Le distanze raggiungibili in questo modo sono dell’ordine dei 107 pc

La stella più luminosa di una galassia
Le stelle più luminose che conosciamo, sono le cosiddette Ipergiganti o supergiganti estreme, appartenenti alla classe di luminosità 0 (zero), tutte con magnitudine intorno a -9, indipendentemente dal tipo spettrale. Ipotizzando che la stella più brillante di una galassia sia una ipergigante se ne può stimare la distanza.

 

Le distanze fino a qualche centinaio di Megaparsec

 

Tully-Fisher e Supernovae

Relazione di Tully-Fisher: la larghezza della riga di 21 cm
Nel 1977 Tully e Fisher hanno dimostrato che esiste una relazione tra la magnitudine assoluta di una galassia a spirale e la velocità di rotazione della galassia, determinata misurando la larghezza della riga a 21 cm dell’idrogeno neutro che popola le sue spire.
L   = 180 V4
Con V in Km/s ed L   in unità di luminosità solare L .
La base fisica di tale relazione riposa sul fatto che la luminosità di una galassia è proporzionale da una parte al numero di stelle che la compone e quindi alla sua massa (L µ M) e dall’altra alle dimensioni della galassia e quindi all’entità della sua superficie emittente (L µ R2).
Essendo la galassia un sistema rotante in equilibrio dinamico possiamo eguagliare forza centrifuga e forza centripeta

ed esplicitare la massa, ottenendo così la nota relazione del viriale

che, espressa in masse solari, diventa

dove M = 2 1033 g

Assumendo ora per le galassie a spirali un rapporto M/L costante e pari a (in unità solari), sostituendo si ottiene

Si assuma infine come brillanza superficiale media di una galassia il valore 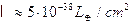) per il raggio medio al quadrato (R = 50.000 al). In tal modo la relazione tra luminosità assoluta e raggio può essere scritta

che, sostituita nella relazione precedente, fornisce

e in definitiva

Si noti come, se V è in Km/s, sia necessario introdurre un coefficiente 105 per trasformare la velocità in cm/s e renderla così omogenea con le altre grandezze. Avremo perciò

Per trasformare la luminosità assoluta in magnitudine assoluta, scriviamo la relazione di Pogson

dove
MG =Magnitudine assoluta della galassia
MS = Magnitudine assoluta del sole = 4,8
LG = Luminosità assoluta della galassia in unità solari
L = Luminosità assoluta del sole in unità solari = 1

da cui

e quindi

In definitiva la magnitudine assoluta della galassia viene ad essere legata alla sua velocità di rotazione. Quest’ultima può essere stimata misurando l’allargamento della riga a 21 cm dell’idrogeno neutro. Infatti la radiazione proveniente dal lato della galassia che si allontana è affetta da un red-shift, mentre la radiazione proveniente dal lato della galassia che si avvicina presenta un blu-shift. Il risultato è che tutte le righe spettrali risultano contemporaneamente spostate di un’egual percentuale sia verso destra che verso sinistra e quindi allargate in misura tanto maggiore quanto maggiore è la velocità di rotazione della galassia.
I moderni telescopi sono in grado di misurare la larghezza della riga di 21 cm fino a circa 100 Mpc.

Le supernovae
Le supernovae sono esplosioni stellari di enorme potenza. Si dividono in supernovae di tipo I (suddivise in Ia e Ib) e tipo II. Le supernove di tipo II e di tipo Ib presentano una magnitudine assoluta al massimo intorno a -18, mentre le supernove di tipo Ia raggiungono al massimo i -20.
Con queste candele standard si raggiungono distanze dell’ordine dei 108 -109 pc.

 

Le distanze fino a qualche migliaio di Megaparsec

 

Galassie più luminose, Lenti gravitazionali e Legge di Hubble

Si tenga presente che attualmente la porzione di universo osservabile (distanza-orizzonte) ha proprio questo ordine di grandezza che, per un universo euclideo, vale

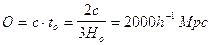
dove h è un fattore di incertezza sul valore della costante di Hubble

La galassia più luminosa di una ammasso di galassie
Si è statisticamente rilevato che le galassie più luminose di un ammasso di galassie sono in genere delle ellittiche giganti con magnitudine assoluta intorno a -23. Le distanze stimate in questo modo sono dell’ordine di 109 pc

Le lenti gravitazionali
La relatività generale prevede che la radiazione elettromagnetica venga deflessa passando accanto ad una forte concentrazione di massa. In questo modo la luce proveniente da oggetti molto distanti (quasar ad esempio), può essere deflessa da un oggetto massiccio (ad esempio una galassia o un ammasso di galassie) interposto sulla nostra linea di vista e concentrata verso di noi con un meccanismo analogo a quello di una lente. L’effetto “lente gravitazionale” è già stato osservato sotto forma di immagini multiple di quasar lontani.

Se l’oggetto interposto G non è perfettamente allineato (condizione d’altra parte maggiormente probabile) si formano due immagini (Q1 e Q2) del quasar Q disposte sulla sfera celeste in modo non simmetrico (a1 ¹ a2) rispetto a G. Ciò comporta che i raggi luminosi che formano le due immagini sdoppiate compiono un percorso di lunghezza diversa (d1 >  d2) per giungere sino a noi.
La relatività generale permette di calcolare la differenza di percorso in termini relativi ().
Supponiamo ad esempio di trovare che d1 risulta essere di un miliardesimo più lungo di d2   e di osservare un aumento di luminosità nell’immagine Q2 che si ripeta identico dopo 3 anni nell’immagine Q1. Possiamo allora dedurre che la differenza di percorso (d1 - d2) deve essere pari a 3 anni-luce. Essendo poi la differenza tra i due tragitti molto piccola possiamo porre d » d1 » d2 e scrivere pertanto

e quindi

trovando così che la distanza d del quasar è di 3 miliardi di anni-luce.

 

Legge di Hubble
Nel 1929 Hubble giunse a definire una relazione che legava la distanza delle galassie all'entità del loro red-shift z e quindi, essendo z = v/c, alla loro velocità di allontanamento.
v =  H D

dove v è la velocità di allontanamento in km/s, D è la distanza in megaparsec (Mpc) e H è una costante di proporzionalità, detta costante di Hubble, alla quale si dà oggi (Ho) un valore compreso tra 50 e 100  km s-1 Mpc-1 (chilometri al secondo per megaparsec).
Introducendo il parametro di red-shift 'z' ( dove z = Dl/l = v/c), la relazione diventa

zc = H D

In tal modo la misura del red-shift di ciascuna galassia diventa una misura, oltre che della sua velocità di recessione v, anche della sua distanza D. E' in questo modo che gli astronomi hanno calcolato la distanza degli oggetti celesti più remoti, come radiogalassie e quasar.
Per tener conto dell'incertezza relativa al valore di Ho e per uniformare la trattazione si usa introdurre un parametro (fattore di Hubble) definito come

e quindi Ho vale   

Poichè il valore di Ho  è compreso tra 50 e 100 è evidente che h può assumere valori compresi tra 0,5 e 1. Così se vogliamo utilizzare la relazione di Hubble per determinare la distanza di oggetti lontani, dovremo scrivere

dove i valori di distanza vengono dati a meno di un fattore h-1. 

La relazione di Hubble è poco affidabile per distanze inferiori ai 50 Mpc, in quanto al di sotto di questo limite i movimenti locali (velocità peculiari » 103 km/s) sono dello stesso ordine di grandezza del moto di recessione. Per distanze inferiori a 50 Mpc la velocità di recessione è infatti v < 5000h km/s.

 

 

 

 

 

 

Appendice 2 -  Composizione moti orbitali

Dati:
Newcomb (1900)
Anno sidereo              = 365,25636 gsm (giorni solari medi)            (-9,5 10-5 s/y)
= 365d 6h 9m 10s         = 31.558.150 s           
Anno anomalistico     = 365,25964 gsm
= 365d 6h 13m 53s       = 31.558.433 s            (-0,26 s/cen)                          
Anno tropico              = 365,24220 gsm
= 365d 5h 48m 46s       = 31.556.926 s            (-5,305 10-3 s/y)         

Stime attuali
Anno sidereo              = 365,256363 gsm
Anno anomalistico     = 365,259635 gsm
Anno tropico              = 365,242190 gsm

Giorno sidereo            = 23h 56m 4,0989s       = 86164,0989 s

Giorno siderale           = 23h 56m 4,0905s       = 86164,0905 s
  - Velocità angolare rotazionale Terra: 2p/86164,1 = 7,2921151 10-5 rad/s = 15,041067 ² s-1

Mese sidereo              = 27d 7h 43m 11,5s         27,321661 gsm                       = 2.360.591,5 s          
Mese sinodico            = 29d 12h 44m 2,9s         29,530589 gsm                       = 2.551.442,9 s
Mese anomalistico      = 27d 13h 18m 33,2s      27,554551 gsm                       = 2.380.713,2 s
Mese draconico          = 27d 5h 5m 35,8s           27,212220 gsm                       = 2.351.135,8 s

 

Giorno solare ed Equazione del Tempo E

 

Le velocità angolari seguono delle regole di composizione identiche a quelle utilizzate per comporre le velocità lineari.
Se wrot e wriv sono rispettivamente la velocità di rotazione e di rivoluzione della terra rispetto alle stelle fisse, allora la velocità di rotazione della terra rispetto al sole può ottenersi componendo i due movimenti e sarà pari a (wrot - wriv). Essendo entrambi i moti diretti (antiorari) il loro segno sarà concorde.

da cui si ricava che il giorno solare dura

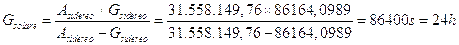
86400 - 86164,0989 = 235,9011 s ˜ 3m 55,9s più del giorno sidereo

In realtà il giorno solare non ha sempre la stessa durata costante di 24 ore. Essa varia infatti con periodicità nel corso dell’anno a causa dell’eccentricità e dell’inclinazione (o obliquità) dell’orbita terrestre. Il valore di 24 ore che noi utilizziamo rappresenta il giorno solare medio, media dei 365 giorni solari.

 

Effetto dell’eccentricità
Per la seconda legge di Keplero in perielio la Terra si muove più velocemente intorno al sole e quindi in 24 ore si sposta rispetto ad esso di un tratto leggermente superiore di 1°. La velocità di rotazione terrestre è invece costante e per compiere un po' più di 1° di rotazione al fine di riavere il sole in culminazione impiegherà un po' più di 4 minuti. Il giorno solare in perielio è un po' più lungo di 24 ore. Per ragioni opposte il giorno solare in afelio raggiunge la sua durata minima, inferiore alle 24 ore.

La velocità di rivoluzione della Terra alla distanza R dal Sole può essere calcolata con la seguente relazione

dove
G =  costante di gravitazione universale = 6,67428 10-11
a = semiasse maggiore (J2000) =  1.0000001124 UA = 149.597.887.506 m
e = eccentricità orbitale (J2000) = 0.01671022
MT= Massa della Terra = 5,9736 1024 kg
MS = Massa del Sole = 1,9891 1030 kg

La velocità massima si ha in perielio, in corrispondenza del raggio minimo Rmin = a(1-e)

La velocità minima si ha in afelio, in corrispondenza del raggio massimo Rmax = a(1+e)

Le rispettive velocità angolari ω (in rad/s) si ottengono dividendo le velocità lineari per il Raggio corrispondente

Calcoliamo la durata del giorno solare vero in perielio componendo la velocità di rotazione della terra rispetto alle stelle fisse con la sua velocità massima di rivoluzione.

da cui

Dunque, per effetto della diversa velocità orbitale della Terra, il giorno solare vero in perielio dura 86408,1160 - 86164,0989 = 244,0171 s = 4 min 4,0 sec più del giorno sidereo e 86408,1160 – 86400 = 8,1160 s più del giorno solare medio

Calcoliamo la durata del giorno solare vero in afelio

da cui

Dunque, per effetto della diversa velocità orbitale della Terra, il giorno solare vero in afelio dura 86392,2957 - 86164,0989 = 228,1968 s = 3 min 48,2 sec più del giorno sidereo e 86400 - 86392,2957 = 7,7043 s meno del giorno solare medio

La durata del giorno solare varia dunque, per effetto della diversa velocità orbitale della Terra, di 244,0171 – 228,1968 = 15,8203 secondi nel corso dell’anno, valore che rappresenta la massima escursione nella durata del giorno solare causata dall'eccentricità dell'orbita terrestre.

Per rappresentare tale variazione durante tutto l'anno, assumiamo che l'andamento sia sinusoidale (in verità non lo è, ma l'eccentricità dell'orbita terrestre è molto piccola e dunque l'approssimazione è ottima). Inoltre sappiamo che, rispetto al valore medio, avremo la durata massima al perielio (intorno al 3 gennaio), mentre quella minima all'afelio (intorno al 4 luglio). L'ampiezza del coseno è ovviamente la metà dell'escursione totale precedentemente calcolata (15,82/2 = 7,91s). Il ciclo è di un anno tropico (365,2422 giorni solari medi)

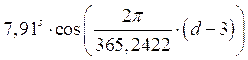
dove d è il numero di giorni dall’inizio dell’anno
d = 1 (1 gennaio)
d = 2 (2 gennaio)
…..
d = 365 (31 dicembre)

Gli scarti però si accumulano nel corso dei giorni, e dunque per sapere quanto tempo ritarda o anticipa il Sole vero rispetto al Sole medio in un certo giorno, occorre tenere conto di tutti gli scarti precedenti. Matematicamente questa operazione si realizza integrando la funzione precedentemente trovata.
L'integrale del coseno è il seno, la periodicità e la fase rimangono le stesse. Per calcolare la massima variazione accumulata basta sommare tutti i contributi che appartengono alla stessa semionda positiva (o negativa).
Se dunque indichiamo con A la durata dell'anno (365,2422 giorni) si avrà

Possiamo ora scrivere l'espressione dell'equazione del tempo dovuta all'eccentricità dell'orbita terrestre. L'ampiezza del seno è ovviamente la metà dell'escursione totale precedentemente calcolata (15,327m/2=7,66m)

Effetto dell’inclinazione (obliquità) dell’orbita

Come abbiamo già detto, dopo un giorno sidereo la Terra si è spostata di circa un grado lungo la sua orbita intorno al Sole e dunque dovrà coprire quest’angolo con un ulteriore rotazione. Possiamo descrivere lo stesso fenomeno pensando che la Terra sia ferma e che il Sole si muova lungo l’eclittica.

L'asse di rotazione della Terra è inclinato sul piano dell'eclittica e così anche l'orbita apparente del sole. Il piano dell'eclittica è inclinato rispetto all'equatore celeste di ε = 23,44°. La proiezione della posizione del Sole sull'equatore celeste introduce un'altra variazione periodica sulla durata effettiva del giorno solare.

Quando il Sole attraversa l’equatore in corrispondenza dei punti equinoziali la sua proiezione sull’equatore si muove più lentamente di quanto non faccia il Sole medio ed il giorno solare vero risulta più breve del giorno solare medio. Quando invece si trova in corrispondenza dei punti solstiziali, il Sole si muove parallelamente all’equatore, la sua proiezione sull’equatore si muove più rapidamente di quanto non faccia il Sole medio ed il giorno solare vero risulta più lungo del giorno solare medio.

Per rendercene conto immaginiamo che il Sole si trovi nel punto gamma (equinozio di primavera) e che sia in culminazione (mezzogiorno) sul meridiano A. Dopo un giorno sidereo la Terra ha compiuto una rotazione di 360° rispetto alle stelle fisse, ma il meridiano A non ritrova il Sole in culminazione, perché il Sole si è spostato lungo l’eclittica di circa 1°. Poiché tuttavia l’eclittica è inclinata di 23,44° rispetto all’equatore, il sole non si è spostato di 1° in longitudine, ma di 1° cos(23,44°)= 0,9175°. Sarà quindi sufficiente che la Terra ruoti di 0,9175° per ritrovare il Sole in culminazione, impiegandoci dunque non 235,90 s, ma 235,90 x cos(23,44°) = 216,43 s.
Il valore 235,90 s (differenza tra il giorno solare medio ed il giorno sidereo) rappresenta dunque il tempo medio tra il tempo minimo impiegato in corrispondenza dei punti equinoziali ed il tempo massimo impiegato nei punti solstiziali pari a 235,90 / cos(23,44°) = 257,12 s



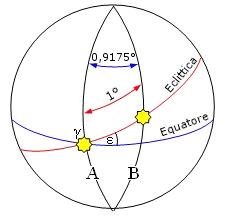
La durata del giorno solare varia dunque, per effetto della obliquità dell’orbita terrestre, di 257,12  – 216,43 = 40,69  secondi nel corso dell’anno..

Anche in questo caso, per rappresentare tale variazione durante tutto l'anno, assumiamo che l'andamento sia sinusoidale. Inoltre sappiamo che, rispetto al valore medio, avremo la durata massima in corrispondenza dei solstizi, mentre quella minima agli equinozi. L'ampiezza del coseno è ovviamente la metà dell'escursione totale precedentemente calcolata (40,69/2 = 20,345s). Il ciclo è semestrale (365,2422/2=182,6211 giorni solari medi)

dove d è il numero di giorni dall’inizio dell’anno e l’81mo giorno dell’anno è l’equinozio di primavera in corrispondenza del quale si presenta il primo minimo..

Come in precedenza, per calcolare gli scarti che si accumulano con il passare dei giorni integriamo la funzione precedente. Per calcolare la massima variazione accumulata basta sommare tutti i contributi che appartengono alla stessa semionda positiva (o negativa).
Se dunque indichiamo con A la durata dell'anno (365,2422 giorni) si avrà

Possiamo ora scrivere l'espressione dell'equazione del tempo dovuta all'obliquità dell'orbita terrestre. L'ampiezza del seno è ovviamente la metà dell'escursione totale precedentemente calcolata (19,711m/2=9,86m)

Equazione del tempo
Per ottenere la durata reale del giorno (giorno vero) è necessario sommare gli effetti dell’eccentricità e dell’obliquità. Le due componenti con periodi di un anno e di 6 mesi sono sfasate perchè la posizione del perigeo non coincide ne’ con un equinozio, ne’ con un solstizio.
Sommiamo prima le equazioni relative alla durata di un singolo giorno senza tener conto degli effetti cumulativi.

Osserviamo che il giorno solare più corto è il 14 Settembre (circa 22 secondi in meno del giorno solare medio), mentre il giorno più lungo è il 21 dicembre (circa 28 secondi in più del giorno solare medio). Sono differenze piccole, che  però si accumulano nel corso dell'anno raggiungendo anche parecchi minuti prima  di cambiare segno.

Sommiamo ora le equazioni relative alla durata di un singolo giorno tenendo conto degli effetti cumulativi.

 

Osserviamo che il giorno solare vero più lungo cade il 44mo giorno dell’anno (13 febbraio) e quello più corto cade il 304mo giorno dell’anno (31 ottobre). Inoltre il giorno vero dura esattamente 24 ore come il giorno solare medio 4 volte all’anno
giorno 106 (16 aprile)
giorno 164 (13 giugno)
giorno 243 (31 agosto)
giorno 358 (24 dicembre)

L’equazione del tempo E tiene conto di questi effetti cumulativi e permette di trasformare il tempo medio M (misurato da un orologio) nel tempo vero T (misurato da una meridiana) e viceversa e viene definita come
T = M + E.
Si noti come, se T è maggiore di M, sarà necessario sottrarre ad M il valore di E per ottenere il tempo vero T.  Se, ad esempio, il tempo vero T è pari a 24h 10m, quando l’orologio segna mezzanotte (tempo medio M), il giorno vero T non è ancora terminato (mancheranno ancora 10 minuti) e dunque per calcolare l’ora vera devo sottrarre ad M la maggior durata di T.
Per questo motivo i segni delle due componenti (eccentricità e obliquità) dovranno essere cambiati e l’equazione del tempo E si scrive

Si tenga infine presente che in alcuni vecchi testi l’equazione del tempo viene definita come M = T + E. Si tratta di una formulazione legata al passato, quando la vita era regolata sul sole e quindi sul tempo vero T ed era dunque più utile trasformare l’ora indicata da una meridiana (T) nell’ora indicata da un orologio meccanico (M). Se si utilizza quest’ultima formulazione non è ovviamente necessario cambiare i segni delle due componenti nell’equazione del tempo.

 

Calcolo mese sidereo

 

Velocità angolare orbitale Terra =
Velocità angolare orbitale Luna =

Dopo un mese sinodico (Msin) la terra si è spostata rispetto al sole di un angolo .
La luna, per tornare in congiunzione, dovrà coprire il medesimo angolo e, alla velocità wL, impiegherà un tempo

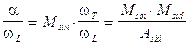
Il mese sinodico sarà pertanto uguale al mese sidereo più il tempo impiegato dalla luna per coprire l’angolo a

e, riordinando

Movimento linea dei nodi e degli apsidi lunari

 

Sia wnod la velocità angolare della linea dei nodi rispetto alle stelle fisse e wL la velocità angolare orbitale della luna rispetto alle stelle fisse. Possiamo considerare ora la velocità relativa della Luna rispetto ai nodi, come differenza delle due velocità precedenti (wL - wnod). Possiamo cioè pensare che i nodi siano fermi rispetto alle stelle fisse e che la luna si muova rispetto a queste con una velocità comprendente anche quella dei nodi.

Si pensi ad un’autovettura A che viaggia a 50 km/h verso un’autovettura B, la quale si avvicini a sua volta a 30 Km/h. Il risultato è il medesimo se si considera una delle due autovetture ferme e l’altra con una velocità pari a (50 - (-30) = 80 Km/h. Nel caso in cui l’autovettura B si stia allontanando nella stessa direzione di A, la sua velocità relativa risulta pari a (50 - 30 = 20 km/h). Si noti come i valori delle velocità abbiano segno concorde se il loro verso è il medesimo, discorde se il verso è contrario.

La Luna impiega un mese draconico (Mdra) a percorrere un’orbita rispetto ai nodi. Possiamo pertanto scrivere

e quindi

I nodi ruotano quindi in senso retrogrado (orario) rispetto alle stelle fisse alla velocità di circa 19° all’anno e impiegano pertanto

per effettuare una rotazione completa.

Analogamente possiamo calcolare la velocità di rotazione degli apsidi lunari rispetto alle stelle fisse
La Luna impiega un mese anomalistico (Man) a percorrere un’orbita rispetto agli apsidi. Possiamo pertanto scrivere

e quindi

Gli apsidi lunari ruotano quindi in senso diretto (antiorario) rispetto alle stelle fisse alla velocità di circa 41° all’anno e impiegano pertanto

per completare una rotazione.

 

Rotazione linea degli apsidi terrestri (moto diretto del perielio)

 

La terra impiega un anno anomalistico Aan a percorrere un orbita rispetto agli apsidi (ad esempio da perielio e perielio). Potremo pertanto scrivere

ed in definitiva

La linea degli apsidi si muove dunque di  moto antiorario, concorde con quello di rivoluzione della terra. Ciò porta ad una diminuzione della velocità di rivoluzione della terra rispetto agli apsidi. La rotazione completa della linea degli apsidi rispetto alle stelle fisse si completa quindi in un periodo di

 

Precessione degli equinozi

La prima stima moderna della velocità di precessione degli equinozi si deve a Newcomb (1896) che trovò per l’anno 1900 il valore weq = 50,256 + 2,22 10-4 ²/y, che riportato al 2000, fornisce 50,278²/y.
Le stime più recenti dell’IAU (Unione Astrofisica Internazionale) danno per il 2000 un valore pari a 50,290966² per anno giuliano (365,25 gsm), pari a 3.8246989 10-5 °/d

Il moto di precessione della linea degli equinozi (precessione generale) è prodotto dall’effetto del sole (precessione solare - 34,6²/y), della luna (precessione lunare - 15,8²/y) e dei pianeti in senso diretto (precessione planetaria 0,12²/y). L’effetto cospirante del sole e della luna si dice precessione lunisolare.
Il fenomeno della precessione fu scoperto da Ipparco di Nicea nel 139 a.C., osservando che le longitudini eclitticali delle stelle erano tutte aumentate di una stessa quantità (circa 2°) rispetto ai valori misurati nel 283 a.C. da Timocari. Poiché la longitudine eclitticale è la distanza angolare di una stella rispetto al punto g (equinozio di primavera), se ne deduce che tale punto si era spostato nell’arco di 144 anni di  circa 2° = 7200” (circa 50” all’anno).

La velocità di rotazione del punto gamma rispetto agli apsidi è pari a

Il punto gamma completa dunque una rotazione rispetto agli apsidi (sempre in senso retrogrado) in un periodo di circa

In altre parole ogni 21.000 anni circa l’asse terrestre esegue una rotazione completa rispetto alla linea degli apsidi e le stagioni si ribaltano ogni 10.500 anni.

Nel 2000 i solstizi disteranno dagli apsidi circa 13° (12,9442° = 46 600” - Meeus 1985). Tale angolo è coperto in

Se ne deduce che intorno al  1250 d.C. il solstizio d’estate coincideva con l’afelio (coincidenza apsidi - solstizi). Poiché, infine, la linea degli equinozi compie un quarto di giro ogni 5.250 anni circa (21.000/4) gli equinozi verranno a coincidere con gli apsidi (equinozio di primavera in perielio) verso il 6500 d.C.

In modo analogo possiamo calcolare il periodo di rotazione della linea degli equinozi (weq) rispetto alle stelle fisse

detto anno platonico.
(Anno platonico = 25.770 anni tropici).

Tenendo conto che una costellazione dello zodiaco ha un’ampiezza di 30°, gli equinozi (ed i solstizi) percorrono ciascuna costellazione in 1/12 di anno platonico, pari  a circa 2.150 anni. Se l’equinozio di primavera cadeva 2000 anni fa nella costellazione dell’Ariete, oggi cade nei Pesci.

 

Anno Tropico

L’anno tropico viene spesso definito come il tempo necessario affinché il sole compia una rivoluzione rispetto al punto gamma (intervallo tra due equinozi di primavera). In realtà il valore che viene normalmente associato all’anno tropico (365,242190 gsm) è un valore medio (anno tropico medio). Infatti la durata dell’anno tropico dipende dal punto dell’orbita che si prende come riferimento ed il suo valore è ad esempio diverso se lo si misura rispetto all’equinozio d’autunno o ad uno dei due solstizi.
La causa di tali differenze va ricercata nel fatto che la terra non completa la sua orbita quando ritorna allo stesso equinozio o allo stesso solstizio (per il moto di precessione di tali punti) ed il tratto parziale di orbita che ha percorso viene compiuto in tempi differenti in relazione alla diversa velocità con cui si muove nei diversi punti della sua orbita.

La velocità lineare (v) e angolare (w) della terra lungo la sua orbita dipendono dalla sua distanza R dal sole secondo le relazioni

con
MS (massa del Sole) = 1.9891 1033 g
MT (massa della Terra) = 5,9742 1027 g
G (costante di gravitazione universale) = 6,67259 10-8
a (distanza media Sole-Terra = semiasse maggiore dell’orbita = 1 UA) = 1.4959787 1013 cm

Calcoliamo la sua velocità media rispetto all’orbita

Possiamo allora calcolare la durata dell’anno tropico medio sottraendo all’anno anomalistico (tempo necessario per percorrere l’intera orbita da perielio a perielio) il tempo mediamente necessario alla Terra per coprire l’angolo di precessione che fa annualmente slittare  equinozi e solstizi rispetto agli apsidi (61,9 secondi d’arco)

L’anno tropico è dunque mediamente 0,01745 giorni più breve dell’anno anomalistico (365,25964 - 0,01745 = 365,24219).
Se consideriamo la velocità massima (in perielio) e minima (in afelio) con cui la terra si muove possiamo calcolare quale è il valore minimo e massimo che può assumere l’anno tropico.

La distanza R della terra dal sole si può determinare scrivendo l’equazione in coordinate polari di un’ellisse

dove
e (eccentricità dell’orbita terrestre) = 0,01672
a (distanza media Sole-Terra = semiasse maggiore dell’orbita = 1 UA) = 1.4959787 1013 cm
q = angolo antiorario che il raggio vettore R forma con la direzione sole-perielio
Poiché
q = 0° in perielio e cos 0° = 1
q = 180° in afelio e cos 180° = -1
le corrispondenti distanze minima e massima valgono

Utilizzando la distanza minima si otterrà la velocità massima (in perielio), mentre la distanza massima fornirà la velocità minima (in afelio)

 

il tempo minimo e massimo necessario alla Terra per coprire l’angolo di (61,9 secondi d’arco)

L’anno tropico può quindi durare approssimativamente dai 24 ai 26 minuti in meno dell’anno anomalistico, a seconda del punto dell’orbita che si prende come riferimento.

Tenendo conto che attualmente la linea degli equinozi forma un angolo di circa 13° con la linea degli apsidi è possibile stimare la durata dell’anno tropico rispetto ai quattro diversi punti equinoziali e solstiziali.

La distanza Terra-Sole e la velocità angolare nei punti equinoziali e solstiziali possono essere calcolate conoscendo l’angolo q che il raggio vettore forma con la direzione Sole-Perielio. Tale angolo vale rispettivamente

Equinozio Primavera  q = 90°   - 13°             R = 1,4900 1013 cm                w = 0.04140 arcsec/s
Solstizio Estate           q = 180° - 13°             R = 1,5203 1013 cm                w = 0.03976 arcsec/s
Equinozio Autunno    q = 270° - 13°             R = 1,5012 1013 cm                w = 0.04078 arcsec/s
Solstizio Inverno        q = 360° - 13°             R = 1,4716 1013 cm                w = 0.04243 arcsec/s

Si determina di conseguenza la relativa lunghezza dell’anno tropico come differenza rispetto all’anno anomalistico

                                                                   Aan - Atr                               Anno Tropico                 AGr - Atr

Equinozio Primavera                          1.495 s = 0,01730 d               365,24233                  0,00017 d
Solstizio Estate                                  1.557 s = 0,01802 d               365,24161                  0,00089 d
Equinozio Autunno                           1.518 s = 0,01757 d               365,24207                  0,00043 d
Solstizio Inverno                                1.459 s = 0,01689 d               365,24275               -   0,00025 d

Media                                                 1.507 s = 0,01745 d               365,24219                  0,00031 d

Sull’ultima colonna compare la differenza tra l’anno gregoriano (365,2425) e l’anno tropico. Si noti come l’assunzione dell’Equinozio di Primavera come punto di riferimento per la misura dell’anno tropico rende attualmente minima la sfasatura con il calendario gregoriano.

 

NOTA
Gli algoritmi di Meeus (1985) generano per il 2000 una durata dell’anno tropico (misurata in tempo delle effemeridi ET) leggermente diversa

                                                                                                Anno Tropico                 AGr - Atr

Equinozio Primavera                                                 365,242377                0,000123 d
Solstizio Estate                                                          365,241629                0,000871 d
Equinozio Autunno                                                   365,242021                0,000479 d
Solstizio Inverno                                                       365,242744             -   0,000244 d

Media                                                                        365,242193                0,000307 d

Tali durate sono perfettamente coerenti con un angolo di 16,8° tra linea degli equinozi e linea degli apsidi, mentre gli stessi algoritmi forniscono un angolo di 12.9442°.

 

Data degli equinozi e dei solstizi

Per determinare la data degli equinozi e dei solstizi è necessario osservare come la durata dell’anno tropico, precedentemente calcolata per ciascun equinozio e per ciascun solstizio, si riferisca ai cosiddetti equinozi e solstizi medi, in assenza cioè dei fenomeni di nutazione e aberrazione. Gli equinozi ed i solstizi veri possono cadere fino a qualche decina di minuti prima o dopo la data prevista per gli equinozi ed i solstizi medi.

Gli algoritmi di Meeus (1985) generano per il 2000 i seguenti valori per gli equinozi ed i solstizi medi e veri (tempo delle effemeridi ET)

                                                 data giuliana (medio)                 medio                        vero

equinozio di marzo                 2 451 623, 804 397 JD           20d   7h 18m 19,9s        20d   7h 31m
solstizio di giugno                  2 451 716, 562 127 JD           20d   1h 29m 27,8s        20d   1h 46m
solstizio di settembre             2 451 810, 211 722 JD           22d 17h   4m 52,8s        22d 17h  24m
solstizio di dicembre              2 451 900, 054 191 JD           21d 13h 18m   2,1s        21d 13h 36m

Per determinare la data dell’equinozio/solstizio medio in un intervallo di anni non eccessivamente esteso, calcoliamo la differenza X tra anno giuliano (365,25) ed anno tropico. E’ allora facilmente verificabile che:

• se l’anno successivo non è bisestile, l’equinozio/solstizio medio avanza di (6h - X)
• se l’anno successivo è bisestile, l’equinozio/solstizio medio retrocede di (18h + X)

essendo X:

Equinozio di marzo                            X = 365,25 -  365,24233 = 0.00767 d » 662,7 s » 11.045 m
Solstizio di giugno                             X = 365,25 -  365,24161 = 0,00839 d » 724,9 s » 12.082 m
Equinozio di settembre                      X = 365,25 -  365,24207 = 0,00793 d » 685,2 s » 11.419 m
Solstizio di inverno                            X = 365,25 -  365,24275 = 0,00725 d » 626,4 s » 10.440 m

Medio                                                X = 365,25 -  365,24219 = 0,00781 d » 674,8 s » 11.246 m
Ad esempio, partendo dai valori dati per il 2000, si calcola per i 4 anni successivi

Anno	primavera (X = 11.045m)	estate (X = 12.082m)	autunno (X = 11.419m)	inverno (X = 10.440m)
2000	20d   07h 18,332m	21d   01h 29.463m	22d 17h 04,880m	21d 13h 18.035m
2001	20d   13h 07,287m	21d   07h 17.381m	22d 22h 53,461m	21d 19h 07.595m
2002	20d   18h 56,242m	21d   13h 05.294m	23d 04h 42,042m	22d 00h 57.155m
2003	21d   00h 45,197m	21d   18h 53.217m	23d 10h 30,623m	22d 06h 46.715m
2004	20d   06h 34,152m	21d   00h 41.135m	22d 16h 19,204m	21d 12h 36.275m

 

La data degli equinozi e dei solstizi oscilla dunque sia per il meccanismo del calendario (che alterna anni civili di 365 giorni ad anni di 366), sia per i fenomeni di nutazione ed aberrazione. Così l’equinozio di primavera cade il 19/21 marzo 
il solstizio d’estate cade il 20/22 giugno
l’equinozio di autunno cade il 22/24 settembre
il solstizio d’inverno cade il 20/22 dicembre

La data media sta comunque impercettibilmente variando poiché l’anno tropico ha una diversa durata rispetto all’anno gregoriano su cui si basa il nostro calendario. Ad esempio l’equinozio medio di primavera anticipa di 0.00017 giorni all’anno, mentre il solstizio d’inverno posticipa di 0.00025 giorni (dal riallineamento gregoriano del calendario avvenuto verso la fine del 1500 ad oggi l’equinozio ha quindi anticipato di circa 15s mentre il solstizio ha posticipato di circa 22s)

 

Data afelio/perielio

Per determinare la data in cui la terra si trova in corrispondenza degli apsidi è necessario osservare come la durata dell’anno anomalistico si riferisca al baricentro del sistema terra-luna. Così il momento di distanza massima o minima tra il centro della terra ed il centro del sole può differire fino ad oltre un giorno da quello del baricentro.

Gli algoritmi di Meeus (1985) generano per il 2000 i seguenti valori (tempo delle effemeridi ET)

                                        data giuliana                

Perielio                       2 451 547, 510 272 JD           04d  gennaio     00h 15m 26,8s
Afelio                         2 451 730, 140 549 JD           04d  luglio       15h 22m 23,5s

Per determinare la data dell’afelio/perielio medio in un intervallo di anni non eccessivamente esteso, calcoliamo la differenza X tra anno anomalistico ed anno giuliano (365,25).
X = 365,25964 - 365,25 = 0.00964 d » 832,9s » 13,882m

E’ allora facilmente verificabile che:

Per il Perielio

• se l’anno di partenza è bisestile il perielio successivo retrocede di (18h - X)
• se l’anno di partenza non è bisestile il perielio successivo, avanza di (6h + X)

Per l’Afelio

• se l’anno successivo  non è bisestile, l’afelio avanza di (6h + X)
• se l’anno successivo è bisestile, l’afelio retrocede di (18h - X)

 

Ad esempio, partendo dai valori dati per il 2000, si calcola per i 4 anni successivi

Anno	perielio (X = 13.882m) gennaio	afelio (X = 13.882m) luglio
2000	04d   00h 15,447m	04d   15h 22.391m
2001	03d   06h 29,324m	04d   21h 36.273m
2002	03d   12h 43,211m	05d   03h 50.155m
2003	03d   18h 57,093m	05d   10h 04.037m
2004	04d   01h 10,975m	04d   16h 17.919m

 

Anche la data degli apsidi oscilla sia per il meccanismo del calendario, sia per l’azione della luna.

La data media sta comunque lentamente posticipando poiché l’anno anomalistico è ben 0.01714 giorni più lungo dell’anno gregoriano. Ciò significa che la data degli apsidi posticipa di un giorno ogni 60 anni circa (1/0.01714 » 60). Così all’inizio del 1900 la data del perielio oscillava tra il 2/3 gennaio e quella dell’afelio tra il 3/4 luglio, mentre ora oscillano rispettivamente tra il 3/4 gennaio ed il 4/5 luglio.

 

Effetto della precessione sulle coordinate celesti

 

Tenendo presente che l’eclittica è inclinata di 23° 26’ 21” (» 23,44°) rispetto all’equatore celeste è possibile calcolare facilmente l’effetto della precessione sulle coordinate equatoriali (Ascensione Retta e Declinazione).
Detta wg la velocità di rotazione del punto gamma (wg = weq = - 50,291”/y), le componenti di tale velocità lungo l’equatore e lungo il meridiano celeste fondamentale (coluro) sono rispettivamente

 

Giorno siderale

Il giorno siderale è il periodo di rotazione della terra misurato rispetto al punto gamma (intervallo di tempo tra due culminazioni successive del punto gamma). Poiché il punto gamma si muove di moto retrogrado (orario), con una velocità rispetto all’equatore celeste pari a

La velocità di rotazione della terra rispetto al punto gamma sarà al solito pari alla differenza tra la velocità di rotazione della terra rispetto alle stelle fisse e la velocità equatoriale del punto gamma (sempre rispetto alle stelle fisse)

La rotazione della Terra rispetto al punto gamma si completa dunque in un periodo di

detto giorno siderale, il quale risulta pertanto 8,4 10-3 s più breve del giorno sidereo.

 

Appendice 3 - Fotometria

La fotometria studia e misura gli effetti delle radiazioni luminose sull'occhio umano, tentando di determinarne le relazioni (per lo più empiriche) con le grandezze energetiche che caratterizzano la radiazione luminosa.
Il problema si presenta complesso in quanto radiazioni luminose a diversa lunghezza d'onda e a diverso contenuto energetico possono produrre la medesima sensazione visiva.

Chiamiamo radiazione luminosa o luce l'intervallo dello spettro elettromagnetico compreso tra le lunghezze d'onda che vanno da 0,4 a 0,7m  in grado di generare una sensazione visiva al nostro occhio.

Intensità luminosa I

L'intensità di emissione luminosa è la potenza emessa sotto forma di luce entro l'angolo solido unitario (1 steradiante = 1 radiante2).
Ricordiamo che 1 steradiante (sr) è l'angolo solido sotto il quale un osservatore posto al centro di una superficie sferica  vede  una  calotta sferica di superficie R2. Essendo l'intera superficie sferica pari a 4pR2, l'intero angolo solido sarà pari a 4p steradianti.

Nel Sistema SI l'unità fotometrica fondamentale è la candela (cd), che misura l'intensità I di una sorgente luminosa. Essa viene naturalmente definita in funzione di un campione luminoso, convenzionalmente individuato. Un tempo la candela veniva definita come 1/60 dell'intensità luminosa prodotta da 1 cm2 di corpo nero a 2042°K (temperatura di fusione del platino). Nel 1979 la XVI Conferenza Generale dei Pesi e delle Misure definì la candela come l’intensità luminosa di una sorgente di potenza 1/683 W/sr che emette una radiazione monocromatica di 5,40 1014 Hz (l = 555,016 nm)

Flusso luminoso F

Si definisce flusso luminoso F il prodotto dell'intensità luminosa per l'angolo solido W attraverso cui la luce diffonde. La sua unità di misura è la candela . steradiante (cd.sr) o lumen (lm).

 

Una sorgente luminosa puntiforme che diffonda luce in tutte le direzioni (sull'intero angolo solido) produce un flusso luminoso di 4p lumen.

Brillanza B

Per sorgenti estese (non puntiformi) viene definita la brillanza B (o luminanza o splendore) come l'intensità di emissione dell'unità di superficie in direzione ortogonale alla superficie stessa.  Nel caso la direzione di emissione formi un angolo j con la direzione normale alla superficie, la superficie emittente va moltiplicata per cosj. La sua unità di misura è la candela/m2 (o nit (nt), nel Sistema SI) o candela/cm2 (o stilb (sb), nel sistema cgs).

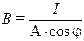
Illuminamento E

Per misurare gli effetti della luce che colpisce una superficie S si definisce l'illuminamento E, come il flusso che colpisce l'unità di superficie S, disposta perpendicolarmente ai raggi luminosi. La sua unità di misura è il lumen/m2 (o lux (lx), nel sistema SI) o lumen/cm2 (nel sistema cgs). Nel caso il flusso formi un angolo q con la direzione normale alla superficie, il suo valore va moltiplicato per cosq.

Una sorgente puntiforme di intensità I posta al centro di una superficie sferica di raggio R incide su di essa con un flusso pari a 4pI lumen. L'unità di area di tale superficie viene perciò illuminata da

Possiamo definire quindi 1 lux come l'illuminamento a cui è sottoposta una superficie di 1 m2 posta alla distanza di 1 m da una sorgente di 1 candela che la illumini ortogonalmente con un flusso di 1 lumen.
La relazione precedente mostra anche come l'illuminamento a cui è sottoposta una superficie è direttamente proporzionale all'intensità luminosa della sorgente ed inversamente proporzionale al quadrato della sua distanza.
Se due sorgenti luminose di diversa intensità ( I1 e I2) e a diversa distanza (R1 e R2) illuminano una superficie allo stesso modo (E = cost) allora deve valere

 

Come è già stato detto uno degli scopi  della fotometria è quello di correlare il flusso luminoso alla potenza (energia per unità di tempo) trasportata dal fascio di radiazione ottica.

Il primo problema che si presenta è legato al fatto che il nostro occhio non è egualmente sensibile a tutte le lunghezze d'onda ottiche, ma presenta un massimo di sensibilità per la luce di 0,555 m (giallo-verde).
Si definisce a tal proposito il coefficiente di visibilità Kl come il rapporto tra il flusso luminoso ed il corrispondente flusso energetico (in watt) portati da una radiazione monocromatica di lunghezza l

Il valore massimo di tale coefficiente si ha appunto per la radiazione di 0,555m e vale

A parità di energia trasportata dal raggio luminoso la sensazione ottica diminuisce di intensità man mano che ci discostiamo da tale lunghezza d'onda. Per determinare l'entità di tale diminuzione si calcola il cosiddetto fattore di visibilità relativa (Vl) di una radiazione ottica di lunghezza d'onda l.

Per determinare il valore di tale fattore per le diverse lunghezze d'onda visibili  è possibile misurare e rapportare l'energia portata da un fascio di radiazione a 0,555m e l'energia trasportata da un fascio di radiazione di lunghezza d'onda l, stimato di egual intensità luminosa (in grado di generare cioè la medesima sensazione ottica).
Il fattore di visibilità relativa varrà dunque 1 per la radiazione di lunghezza 0,555m e assumerà valori via via inferiori per le altre lunghezze d'onda ottiche, azzerandosi intorno a 0,4 e 0,7m.

Possiamo provare a stimare la visibilità media sovrapponendo alla curva una gaussiana normalizzata (media M = 0, scarto quadratico medio s = 1, ordinata massima F(M) = = 0,39894, area totale = 1) in cui i valori estremi (0,4 - 0,7) coincidano con i valori standardizzati -3,5 e +3,5 corrispondenti ad una area praticamente pari ad 1 (> 0,999).

L'ordinata media è pari all'area (1) diviso l'ascissa relativa (+3,5 - (-3,5) = 7) e vale quindi 1/7. Possiamo ora impostare una proporzione tra la gaussiana e la curva di visibilità tra le corrispondenti ordinate massime  e medie
0,39894 :  1  =  1/7  :   x

che ci fornisce una visibilità media di circa il 35,8 %

La relazione che lega il flusso luminoso alla potenza P  del fascio per unità di area  ed alla sezione trasversale S del fascio è

dove l'integrale viene esteso per consuetudine da zero ad infinito, ma si azzera al di fuori dell'intervallo di visibilità poiché in tal caso si annulla Vl.

 

Calcolo quantità fotometriche solari

Integrando l'equazione di Planck per un corpo nero alla temperatura di 5778 °K (temperatura efficace del sole) da 0,39m a 0,72m si ottiene l'emissione ottica unitaria del sole, pari a 2,52 107 watt/m2.
Calcoliamo ora l'emissione ottica totale moltiplicando per la superficie solare (6,087 1018 m2), ottenendo 1,534 1026 watt. Essendo l'energia portata su tutte le lunghezze d'onda del visibile, utilizziamo il fattore medio di visibilità relativa pari a 0,37 per calcolare il fattore di visibilità solare

il flusso del sole varrà allora

La sua intensità luminosa sarà

la sua brillanza

mentre, ricordando che la terra dista dal sole R = 1,496 1011 m,  l'illuminamento solare cui è sottoposta la terra (al di fuori dell'atmosfera) sarà

Fotometria stellare

La prima misura dell'intensità luminosa delle stelle fu naturalmente eseguita confrontando le stelle per mezzo dell'occhio (luminosità visuale). Così Ipparco, nel II sec. a.C., aveva fissato una scala empirica, detta delle magnitudini apparenti (m), comprendente 6 gradi di luminosità. Secondo tale scala la stella più luminosa del cielo risultava essere di prima magnitudine (m = 1) ed era 5 volte più luminosa di una (appena visibile) di sesta magnitudine (m = 6).
Le magnitudini sono dette apparenti poiché il loro valore, a parità di intensità luminosa, dipende anche dalle distanza delle stelle.
Una profonda revisione si ebbe nella seconda metà dell'ottocento quando si scoprì che la sensazione visiva (S) non è direttamente proporzionale all'intensità (l) dello stimolo luminoso percepito, ma al suo logaritmo. Tale relazione viene espressa dalla legge di Fechner e Weber.

che, nel caso di una stella, lega la magnitudine apparente m, alla luminosità apparente l (misurata in genere in lux)

C è una costante (costante di zero) il cui valore dipende dalle unità di misura usate per esprimere la luminosità e dal valore assunto convenzionalmente come zero per la scala delle magnitudini

Poichè tramite registrazioni fotometriche (Herschel) una stella di prima magnitudine risultò essere in realtà 100 volte più luminosa di una di 6 magnitudine, la costante k assume il valore -2,5. Infatti

e quindi
                 k = -2,5

La relazione fondamentale della fotometria stellare diventa quindi (relazione di Pogson)

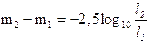
e quindi

passando infine all'antilogaritmo

Se dobbiamo ad esempio confrontare la luminosità di Sirio m = - 1,45 con quella di Aldebaran (m = 0,85)  troveremo

Sirio dunque è apparentemente circa 8,3 volte più luminoso di Aldebaran.

Per ogni grado di magnitudine (m2 - m1 = 1) la luminosità apparente aumenta di circa 2,512 volte. Come per ogni scala convenzionale anche nel caso delle magnitudini apparenti è necessario fissare un punto zero.
Viene dunque definita di magnitudine visuale apparente zero (mvis = 0) una stella che produca (al di fuori dell'atmosfera) un illuminamento di 2,67 10-6 lux.
La costante di zero assume in tal caso il valore

CV = -13,934

Ricordando che il sole fornisce un illuminamento di 1,34 105 lux, possiamo allora calcolarne facilmente la magnitudine apparente (visuale)

La magnitudine visuale è naturalmente correlata al flusso ottico (spettro visibile) che ci proviene dalle stelle. Quando invece si misura il flusso energetico su tutte le lunghezze d'onda, si ottiene la magnitudine bolometrica. Anche in questo caso è necessario fissare un punto zero. Viene definita di magnitudine bolometrica apparente zero (mbol = 0) una stella che produca (al di fuori dell'atmosfera) una potenza unitaria di 2,56 10-5 erg/(s cm2).
La costante di zero assume in tal caso il valore

Cb = -11,48

 

Ricordando che il sole fornisce una potenza unitaria (costante solare) di 1,368 106 erg/(s cm2), possiamo calcolarne la magnitudine apparente (bolometrica)

Qualora si conosca la distanza R di una stella dalla terra se ne può calcolare anche la luminosità intrinseca L (espressa come intensità luminosa o come flusso luminoso)

Sapendo ad esempio che Sirio dista 8,6 al (8,136 1016 m) e che la sua magnitudine apparente vale m = - 1,45 determiniamo:

- l'illuminamento, che è 2,5121,45 = 3,8 volte superiore a Eo e pari quindi a  circa 10-5 lux
- il flusso, pari a 
- l'intensità luminosa, pari a

scopriamo così che Sirio è 21,6 volte più luminoso del sole

Come si vede è scomodo confrontare le luminosità intrinseche delle stelle utilizzando lumen e candele. Si è perciò convenuto di misurare la luminosità intrinseca di una stella utilizzando la scala di Ipparco, dopo aver azzerato le differenze di distanza portando tutte le stelle a 10 parsec.
La magnitudine apparente che una stella verrebbe a possedere se fosse posta a 10 parsec è detta magnitudine assoluta M.

Così una stella di luminosità intrinseca L (flusso) e distanza R, che presenta un luminosità apparente l (illuminamento) pari a

posta a 10 parsec presenterebbe una luminosità apparente l10 pari a

dove k è un coefficiente (pari a 3,0857 1016 m/pc) che trasforma i parsec in m

Applicando la formula di Pogson a questi due valori di luminosità apparente, si ottiene

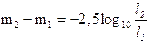
Essendo R/k la distanza della stella espressa in parsec, la relazione diventa

Essendo la quantità (m-M) correlata alla distanza della stella, essa viene detta modulo di distanza.

Sapendo che il sole dista dalla terra 1,496 1011 m pari a 4,848 10-6 parsec, possiamo determinarne la magnitudine assoluta visuale e bolometrica

La magnitudine assoluta di Sirio (m = - 1,45  ; R = 2,64 pc) sarà

La magnitudine assoluta di Aldebaran (m = 0,85  ; R = 18,4 pc) sarà

Così la differenza di magnitudine assoluta tra Sirio e il Aldebaran è 1,44 - (-0,47) = 1,91
Scopriamo così che Sirio è in realtà circa 2,5121,91 = 5,8 volte meno luminoso di Aldebaran.

Tenendo poi conto che la luminosità apparente che segna il punto zero della scala delle magnitudini apparenti è 2,67 10-6 lux (lumen/m2), possiamo trovare il corrispondente valore (M = 0) per la scala delle magnitudini assolute, calcolando la corrispondente luminosità intrinseca visuale a 10 parsec

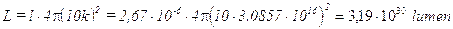
corrispondenti ad un'intensità luminosa di 2,54 1029 candele

Mentre, ricordando che il punto zero delle magnitudini apparenti bolometriche è 2,56 10-5 erg/(s cm2), la corrispondente luminosità intrinseca bolometrica a 10 parsec sarà

In questo modo la relazione di Pogson

può essere utilizzata anche per calcolare la magnitudine assoluta, sostituendo alle luminosità apparenti le luminosità intrinseche della stella e del punto zero

 

Magnitudine assoluta di 1 candela          
Magnitudine apparente di 1 lux                

Formula di Russell
La relazione di Pogson può essere utilizzata per ottenere una relazione tra la Magnitudine, la Temperatura ed il Raggio (in unità solari R la magnitudine visuale assoluta di una stella e del sole possiamo scrivere

Per determinare l’emissione di una stella in corrispondenza di una certa lunghezza d’onda l possiamo ricorrere all’equazione di Planck che descrive il comportamento emissivo di un radiatore perfetto (corpo nero), fornendoci la quantità di energia (erg) emessa, per unità di tempo (s) e di superficie radiante (cm2), da un corpo alla temperatura T (K) in corrispondenza della lunghezza d’onda l (cm).

Possiamo ora stimare l’energia emessa nell’intorno della lunghezza d’onda l, calcolando l’area sottesa all’intervallo Dl centrato in l. In prima approssimazione esso è pari all’area del rettangolo avente base Dl e altezza W(lT).
Nel nostro caso, dovendo valutare l’emissione nel visibile l = 5,5 10-10 cm, la relazione diventa

La luminosità assoluta visuale della stella sarà pari all’energia emessa nel visibile dall’intera superficie.

Sostituendo nella relazione di Pogson, otteniamo

Ricordando che T » 5778 °K, la relazione diventa

e assegnando al sole magnitudine visuale assoluta 4,82 otteniamo

o, esplicitando il raggio,

Se ora, in prima approssimazione, trascuriamo l'unità nella differenza dell’argomento del logaritmo otteniamo la classica relazione di Russell

o, esplicitando il raggio,

E’ possibile costruire una relazione analoga che leghi la magnitudine bolometrica al raggio ed alla temperatura. Indicando rispettivamente con Mbol e Mbol la magnitudine bolometrica assoluta di una stella e del sole possiamo scrivere

Per determinare l’emissione di una stella in corrispondenza di tutte le lunghezze d’onda  possiamo ricorrere all’equazione di Stefan-Boltzmann. che descrive il comportamento emissivo di un radiatore perfetto (corpo nero), fornendoci la quantità di energia (erg) emessa, per unità di tempo (s) e di superficie radiante (cm2), da un corpo alla temperatura T (°K) in corrispondenza di tutte le lunghezze d’onda e moltiplicarla per la superficie della stella 4pR2. Essendo dunque

potremo scrivere

Assumendo infine per la temperatura e la magnitudine assoluta bolometrica del sole i valori T  = 4,75 si ottiene

Confrontiamo ora tale relazione con la relazione

Eguagliando i due secondi membri ed esplicitando la differenza tra Mbol e MV si ottiene

o, trascurando ancora l’unità nella differenza,

Il valore così ottenuto viene definito correzione bolometrica BC.
La correzione bolometrica viene in realtà calcolata tramite modelli più sofisticati relativi alle atmosfere stellari. Il valore zero della scala è stato convenzionalmente fissato in modo che sia BC = 0 per stelle con Te = 6580 °K (tipo spettrale F5).

Indici di colore

Quando in astronomia iniziarono ad essere utilizzate le emulsioni fotografiche fu possibile ottenere anche valori di magnitudine fotografica (Mpg). I valori ottenuti sono in genere tra loro diversi in quanto l'occhio presenta un massimo di sensibilità nel giallo-verde, mentre la lastra fotografica nel blu-violetto. Applicando ad una macchina fotografica un filtro giallo si riesce a simulare la sensibilità dell'occhio umano e le magnitudini così ottenute sono dette fotovisuali (Mpv).

Le magnitudini ottenute con un fotometro sono dette fotoelettriche. Le magnitudini fotoelettriche vengono determinate in corrispondenza di particolari intervalli di lunghezze d'onda. In genere si ottengono per l'ultravioletto (MU o U) per il blu (MB o B) e per il giallo (visuali) (MVo V) .
La magnitudine fotoelettrica B è correlabile alla magnitudine fotografica (MB = Mpg + 0,11), mentre la magnitudine fotoelettrica V corrisponde alla magnitudine visuale o fotovisuale.

Le differenze nei valori di magnitudine misurati nei diversi intervalli di lunghezze d'onda sono importanti poiché sono correlabili alla temperatura superficiale di una stella. Infatti per la legge di Wien un corpo nero che aumenta la sua temperatura emette in proporzione sempre più energia verso le regioni a minor lunghezza d'onda (blu violetto). Così una stella molto calda presenterà una magnitudine nel blu minore della sua magnitudine visuale, mentre per una stella molto fredda avverrà l'opposto (valori minori di magnitudine corrispondono infatti a luminosità più elevate).

Un indice di colore molto usato è proprio fornito dalla differenza tra la magnitudine fotografica  e la magnitudine visuale (o fotovisuale).
C = Mpg - Mpv = mpg - mpv

Un altro indice  spesso utilizzato è l’indice B-V, dato dalla differenza della magnitudine fotoelettrica nel blu e nel visuale.
La relazione tra questi due indici è approssimativamente

C + 0,11 » B-V

L'indice di colore ha il vantaggio di fornire i valori di temperatura di una stella (nell'ipotesi che essa irradi come un corpo nero) indipendentemente dalla conoscenza della distanza della stella e del suo raggio (e quindi del valore della sua superficie emittente).

Più basso è il valore di tale indice, più la stella emette nel blu e più elevata è la sua temperatura. L'indice di colore del sole è + 0,55, mentre l'indice di colore di una stella a 15.000°K è - 0,27.

Per costruire l'indice di colore si ricorre ad una formulazione approssimata della funzione di Planck che descrive il comportamento emissivo di un radiatore perfetto (corpo nero).

Poichè l'indice di colore viene costruito su lunghezze d'onda del visibile, intorno a 5 10-10 cm, la relazione diventa

ed in tal caso è dunque possibile, per temperature inferiori ai 20.000 °K, trascurare l'unità nella differenza a denominatore ed utilizzare la seguente planckiana approssimata (approssimazione di Wien, per le basse temperature)

Siano ora ml  ed Ml la magnitudine apparente ed assoluta di una stella di raggio R e distanza D, misurate nella radiazione di lunghezza d'onda l.

La luminosità assoluta della stella  sarà pari a

e la sua magnitudine assoluta

La luminosità apparente della stella sarà pari a

e la sua magnitudine apparente

Se ora costruiamo l'indice di colore, come differenza tra le magnitudini (apparenti o assolute) a diverse lunghezze d'onda l1 e l2, otteniamo

 

E' ora facile verificare che costruendo l'indice di colore con le magnitudini assolute si ottiene lo stesso risultato, indipendente sia da R che da D.

Sostituiamo ora la planckiana approssimata ed otteniamo

 

 

Se usiamo ad esempio

l1 = 4,25 10-5 cm, lunghezza di massima emissione nel blu
l2 = 5,48 10-5 cm, lunghezza di massima emissione nella banda del visibile

la relazione diventa

L'indice di colore viene poi tarato fissando la costante di zero in modo che IC = 0 per stelle di classe spettrale A0 (T » 10.000°K). La costante di zero varrà quindi

cost = + 0,555
e la relazione diventa

ed  in definitiva la temperatura di colore è pari a

Se invece utilizziamo

l1 = 4,4 10-5 cm, lunghezza di massima emissione nel blu
l2 = 5,5 10-5 cm, lunghezza di massima emissione nella banda del visibile

Si ottiene l’indice B-V del sistema fotoelettrico U-B-V di Morgan-Johnson

Anche in questo caso la taratura viene effettuata fissando la costante di zero in modo che B-V = 0 per stelle di classe spettrale A0 (T » 10.000°K). La costante di zero varrà quindi cost = + 0,5 e la relazione diventa

ed  in definitiva la temperatura di colore è pari a

Magnitudine ed albedo planetaria (modello elementare)

 

Ipotizziamo che il Pianeta si comporti come un disco di raggio R perfettamente riflettente. Per tener eventualmente conto della forma ellissoidale del Pianeta possiamo usare il raggio di un cerchio avente la stessa aerea dell’ellisse planetario. L’area di un ellisse è pari a pab, con a semiasse maggiore (raggio equatoriale) e b semiasse minore (raggio polare). Per cui il raggio del cerchio avente la stessa area è pari a .

Il flusso luminoso φ che colpisce la Terra proveniente da una sorgente estesa (il disco planetario o il disco solare) è direttamente proporzionale al flusso emesso per unità di superficie w (luminosità unitaria) del corpo emittente e all’angolo solido θ sotto il quale viene vista la superficie emittente da un osservatore posto sulla Terra.
φ = k w θ
Un Pianeta di raggio R posto a distanza D dal Sole intercetta una frazione di energia solare () pari all’area del suo disco planetario pR2 fratto l’area totale della superficie sferica 4pD2 investita dal flusso solare.
Se il Pianeta si comporta come uno specchio piano perfettamente riflettente (albedo A = 1)  la sua luminosità totale sarà .

 

 Il rapporto tra luminosità intrinseca unitaria Pianeta/Sole sarà dunque pari a

L’angolo solido (in steradianti ) sotto il quale osserviamo la superficie del disco planetario è , dove DTS è la distanza Terra-Sole (unità astronomica) pari a circa 149,6 milioni di km.

Dunque il flusso luminoso che colpisce la Terra proveniente dal Pianeta è

poiché tuttavia il Pianeta non riflette integralmente la radiazione proveniente dal Sole, ma solo una frazione di essa, definita albedo A del pianeta, il flusso in arrivo deve essere moltiplicato per tale frazione

mentre il flusso luminoso che colpisce la terra proveniente dal Sole è

Infine, il rapporto tra i due flussi vale

Possiamo ora calcolare la magnitudine apparente del pianeta utilizzando la relazione di Pogson che lega la differenza di magnitudine tra due corpi celesti al rapporto dei loro flussi luminosi ricevuti sulla Terra

Sapendo che la magnitudine apparente del Sole , la relazione diventa

dalla quale è possibile esplicitare l’albedo A del Pianeta, detta albedo geometrica

Calcoliamo, ad esempio, l’albedo di Nettuno sapendo che:

• la sua massima luminosità (in corrispondenza della sua massima vicinanza al Sole ed alla Terra) corrisponde ad una magnitudine apparente pari a m = 7,8
• il suo raggio medio è R = 24624 km = 1,646 10-4 UA
• la sua distanza minima dal Sole (al perielio) è 29,811 UA
• la sua distanza minima dalla Terra è 28,783 UA

Nettuno riflette circa il 41% della luce solare incidente

Fasi planetarie
Nel caso dei pianeti interni (Mercurio e Venere) e di Marte è necessario tener conto delle fasi, cioè del fatto che, come avviene per la Luna, il disco planetario osservabile dalla Terra non è sempre completamente illuminato. Il circolo di illuminazione (perpendicolare alla direzione Sole-Pianeta), proiettato sul disco planetario osservabile dalla Terra, traccia su di esso una semiellisse di semiassi a = R e b = R cos j, dove j è l’angolo di fase, cioè l’angolo Sole-Terra visto dal Pianeta.
La distanza angolare del Pianeta dal Sole (vista dalla Terra) si definisce invece elongazione e.

 

L’area illuminata del disco planetario osservabile dalla Terra sarà dunque pari all’area del semidisco planetario ()

dove  rappresenta la frazione illuminata del disco planetario in funzione dell’angolo di fase j.

 

In definitiva, per un pianeta che presenti il fenomeno delle fasi,  l’angolo solido sarà pari a

ed il flusso

Durante una rivoluzione sinodica dei pianeti interni l’angolo di fase può assumere tutti i valori compresi tra 0 e 2p. Possiamo considerare, in prima approssimazione, costante la distanza Terra-Sole e la distanza Pianeta-Sole, ma non la distanza tra la Terra ed il Pianeta.

Scriviamo allora la distanza Terra-Pianeta in funzione dell’angolo di fase usando il teorema di Carnot

da cui

Il flusso luminoso proveniente dal pianeta diventa allora

 

ed il rapporto tra il flusso luminoso del Pianeta ed il flusso luminoso del Sole

la magnitudine del Pianeta diventa così

 

 

  Appendice 4 – dati e costanti

 

Newcomb (1900)
Anno sidereo              = 365,25636 gsm (giorni solari medi)            (-9,5 10-5 s/y)
= 365d 6h 9m 10s         = 31.558.150 s           
Anno anomalistico     = 365,25964 gsm
= 365d 6h 13m 53s       = 31.558.433 s            (-0,26 s/cen)                          
Anno tropico              = 365,24220 gsm
= 365d 5h 48m 46s       = 31.556.926 s            (-5,305 10-3 s/y)         

Stime attuali
Anno sidereo              = 365,256363 gsm
Anno anomalistico     = 365,259635 gsm
Anno tropico              = 365,242190 gsm

Velocità angolare linea degli apsidi terrestri =

Giorno sidereo            = 23h 56m 4,0989s       = 86164,0989 s
Giorno siderale           = 23h 56m 4,0905s       = 86164,0905 s
- Velocità angolare rotazionale Terra: 2p/86164,0989 = 7,2921151 10-5 rad/s = 15,041067 ² s-1

Mese sidereo              = 27d 7h 43m 11,5s         27,321661 gsm                       = 2.360.591,5 s          
Mese sinodico            = 29d 12h 44m 2,9s         29,530589 gsm                       = 2.551.442,9 s
Mese anomalistico      = 27d 13h 18m 33,2s      27,554551 gsm                       = 2.380.713,2 s
Mese draconico          = 27d 5h 5m 35,8s           27,212220 gsm                       = 2.351.135,8 s

Velocità angolare linea dei nodi lunari =
Velocità angolare linea degli apsidi lunari =

G =  costante di gravitazione universale = 6,67428 10-11
a = semiasse maggiore (J2000) =  1.0000001124 UA = 149.597.887.506 m
e = eccentricità orbitale (J2000) = 0.01671022
MT= Massa della Terra = 5,9736 1024 kg
MS = Massa del Sole = 1,9891 1030 kg

1 Unità Astronomica (UA) = 149.597.870.691 m
1 anno luce (al) = 9,4605284 1017 cm = 9,4605284 1015 m = 9,4605284 1012 km
1 parsec (pc) = 3,0856776 1018 cm = 3,2616334 al
1 parsec cubico (pc3) = 2,938 1055 cm3 = 3,470 101 al3
1 megaparsec (Mpc) = 103 kiloparsec (kpc) = 106 parsec
1 megaparsec cubico (Mpc3) = 2,938 1073 cm3 = 3,470 1019 al3

Costante di Hubble (Ho) = 100 h km s-1 Mpc-1 = 3,24 10-18 h s-1
Tempo di Hubble  (Età massima dell’Universo) = 1/ Ho = 3,1 1017 h-1 s = 1010 h-1 anni
Età Universo euclideo = 2/(3 Ho) = 2,1 1017 h-1 s = 6,5 1010 h-1 anni
Orizzonte Universo euclideo (Raggio osservabile) = 2c/(3 Ho) = 2000 h-1 Mpc = 6,17 1027 h-1 cm
Luminosità media delle Galassie (
Densità numerica media delle galassie = 2 10-2 h3 Mpc-3 = 6,8 10-76 h3 cm-3
Radiazione isotropa di fondo = 2,728 ± 0,004 °K
Densità critica (rc) =1,879 10-29 h2 g cm-3 » 1,1 10-5 h2 barioni cm-3 = 11 h2 barioni m-3
Densità radiazione (rg) = 4,19 10-13 erg cm-3 = 4,66 10-34 g cm-3 = 412 fotoni cm-3
Entropia specifica Universo euclideo (h =  rg /rc = rapporto fotoni/barioni) = 3,68 107 h-2

 

 

Luminosità solare intrinseca (L) = 3,847 1033 erg/s  = 3.847 1026 watt (3.86 1028 lumen = 3.06 1027 candele)
Costante solare = 1,962 cal cm-2 min-1 = 1,368 106 erg cm-2 s-1 = 1,368 103 watt/m2  (1,37 105 lux )
Diametro solare (fotosfera) (D) = 1,392 106 km = 1,392 109 m = 1,392 1011 cm
Raggio solare (fotosfera) (R) = 6,96 105 km = 6,96 108 m = 6,96 1010 cm
Superficie solare (fotosfera) = 6,087 1012 km2 = 6,087 1018 m2 = 6,087 1022 cm2 
Potenza unitaria solare = 6.32 1010 erg cm-2 s-1 = 6.32 107 watt/m2 (5,04 108 nit)
Temperatura solare efficace (di corpo nero) T = 5778 °K
Emissione ottica del sole = 40%
Magnitudine solare assoluta =  visuale 4,83  -  bolometrica 4,75
Magnitudine solare apparente =  visuale -26,74  /  bolometrica -26,82 
Luminosità corrisp. a M = 0 (fuori atm.) visuale 3,171 1030 lumen = 2,523 1029 candele / bolom. 3,015 1035 erg/s
Luminosità corrisp. a m = 0 (fuori atm.)   visuale 2,65 10-6 lumen/m2 (lux) / bolometrica 2,52 10-5 erg/(s cm2)

Raggio terrestre equatoriale (a) = 6.378.388 m (Ellissoide internazionale o di Hayford)
Raggio terrestre polare (b) = 6.356.912 m (Ellissoide internazionale o di Hayford)
schiacciamento polare o ellissoidicità [(a-b)/a] = 1/298,0
Raggio di una sfera avente la stessa superficie della Terra = 6.371.228 m
Raggio di una sfera avente lo stesso volume della Terra = 6.371.221 m
Raggio terrestre equatoriale (a) = 6.378.137 m (valore raccomandato dall'Unione internazionale geofisica e geodesia)
Raggio terrestre equatoriale (a) = 6.356.140  5 m (Ellissoide astrogeodetico)
schiacciamento polare o ellissoidicità [(a-b)/a] = 1/298,257
Precessione generale anno 2000 =  - 50,291” per anno giuliano (365,25 giorni solari medi)
Distanza media Terra-Luna (da centro a centro) 3,844 108 m
Rapporto massa Luna/Terra  0,01230002

 

 

 

 

 

	Mercurio	Venere	Terra	Marte	Giove	Saturno	Urano	Nettuno	Plutone
Dist Media Sole                     (UA) semiasse maggiore a        (106 km)	0,3871 (57,91)	0,7233 (108,2)	1,000 (149,6)	1,524 (227,9)	5,203 (778,4)	9,537 (1426,7)	19,191 (2871,0)	30,069 (4498,3)	39,481 (5906,4)
(1) Eccentricità  e	0,2056	0,00677	0,0167	0,0934	0,04839	0,05415	0,0472	0,00859	0,2488
(1) Perielio                             (UA)                                             (106 km)	0,3075 (46,00)	0,7182 (107,5)	0,9833 (147,1)	1,381 (206,6)	4,951 (740,7)	9,0207 (1349,5)	18,2860 (2735,6)	29,8108 (4459,7)	29,658 (4436,9)
(1) Afelio                                 (UA)                                             (106 km)	0,4667 (69,82)	0,7279 (108,9)	1,0167 (152,1)	1,666 (249,2)	5,455 (816,1)	10,053 (1504,0)	20,0965 (3006,4)	30,3271 (4536,9)	49,304 (7375,9)
Dist. Min. Terra                     (UA)                                          (106 km)	0,517 (77,3)	0,255 (38,2)	- -	0,363 (54,5)	3,934 (588,5)	7,9913 (1195,5)	17,259 (2581,9)	28,783 (4305,9)	28,701 (4293,7)
Dist. Max. Terra                    (UA)                                           (106 km)	1,483 (221,9)	1,745 (261,0)	- -	2,682 (401,3)	6,471 (968,1)	11,086 (1658,5)	21,105 (3157,3)	31,332 (4687,3)	50,356 (7533,3)
(2) Per. rivol. sidereo          (giorni)                                          (anni)	87,969 (0,2408)	224,70 (0,6152)	365,2564 (1)	686,980 (1,881)	4332,589 (11,862)	10759,22 (29,46)	30685,4 (84,01)	60189 (164,8)	90465 (247,7)
(2) Vel. Rivol. media            (km/s)	47,88	35,03	29,79	24,13	13,06	9,65	6,80	5,43	4,74
(3) Periodo riv. sinodico    (giorni)	115,88	583,92	-	779,94	398,88	378,09	369,66	367,49	366,74
(4) Periodo rotaz. sid            (ore)                                          (giorni)	1407,5 (58,65)	-5832,4 (-243,02)	23,9345 (0,99727)	24,623 (1,0259)	9,925 (0,4135)	10,656 (0,444)	-17,24 (-0,718)	16,11 (0,671)	-153,3 (-6,387)
(4) Incl asse su orb             (gradi)	0,00	177,3	23,45	25,19	3,12	26,73	97,86	29,56	122,46
(5) Diam App min/max     (sec arco)	4,5/13	9,7/66,0	-/-	3,5/25,7	29,8/59,0	14,5/20,1	3,3/4,1	2,2/2,4	0,06/0,11
Inclinaz. Orbita su eclitt    (gradi)	7,00	3,395	0,000	1,851	1,305	2,484	0,770	1,769	17,142
Numero satelliti	-	-	1	2	63	62	27	13	3
(6) Raggio equat.                  (km)	2440	6052	6378	3397	71492	60268	25559	24766	-
(6) Raggio medio                  (km)	2440	6052	6371	3390	69910	58230	25362	24624	1137
(6) Schiacciamento a	0,000	0,000	1/298,25	1/154	1/15,4	1/10,2	1/43,6	1/58,5	-
Massa                                   (kg)                                (masse terrestri)	3,30 1023 (0,055)	4,87 1024 (0,81)	5,9742 1024 (1)	6,42 1023 (0,11)	1,90 1027 (317,8)	5,68 1026 (95,2)	8,68 1025 (14,5)	1,02 1026 (17,2)	1,25 1022 0,0021
Densità media                  (kg/dm3)	5,427	5,204	5,515	3,933	1,326	0,687	1,318	1,638	2,05
(7) Gravità all’equatore  (Terra = 1)	0,38	0,91	1	0,38	2,4	0,92	0,89	1,1	0,067
(8) Velocità fuga                  (km/s)	4,3	10,36	11,186	5,03	60,2	36,1	21,4	23,5	1,2
(9) Flusso term solare     (Terra = 1)	6,67	1,91	1	0,431	1/27	1/91	1/368	1/904	1/1559
Magnitudine max	-1,9	-4,4	-3,86	-2,0	-2,7	0,7	5,5	7,8	15,1
(10) Albedo geometrica	0,11	0,65	0,367	0,15	0,52	0,47	0,51	0,41	0,3
(10) Temperatura di corpo nero (K)	442	239	247	217	91	64	36	33	43
Temperatura media                    (K)	440	737	288	210	129	97	58	58	50
Pressione atmosferica         (atm)	10-15	91	1	6 10-3	-	-	-	-	3 10-6

 

(1) Per l’eccentricità e di un ellisse valgono le seguenti relazioni:   

(2) Il periodo P e la velocità media di rivoluzione V possono essere calcolati in funzione della distanza media D (pari al semiasse maggiore a utilizzando la 3a di Keplero:  P2 = k a3      oppure    V2 a = k . Esprimendo tutte le variabili in unità terrestri si ottiene

(3) Il periodo di rivoluzione sinodico Ps si può calcolare componendo la velocità angolare rispetto alle stelle fisse della Terra (wT = 2p/PT) e del Pianeta (wP= 2p/PP). Per i pianeti interni 

(4) Il moto retrogrado è preceduto dal segno meno e, secondo la convenzione recentemente adottata dall'Unione Astronomica Internazionale (IAU), ai pianeti con moto di rotazione retrogrado si assegna inclinazione dell'asse maggiore di 90 gradi.

(5) L’angolo (in radianti) sotto il quale il diametro 2R del pianeta viene osservato dalla Terra (da una distanza D) è pari a 2R/D. Poichè un radiante è pari 360°/2p = 57,29578° = 206264,8 secondi d’arco, il diametro apparente minimo e massimo di un pianeta  si calcola  

(6) Lo schiacciamento polare a di un Pianeta è pari a = (a-b)/a con a raggio equatoriale e b polare. Da cui il raggio polare è b = a (1 - a).  Il raggio medio Rm è pari

(7) La gravità di un Pianeta (in unità terrestri) si calcola facendo il rapporto tra la forza tra la forza di gravità calcolata sul Pianeta e sulla Terra

(8) La velocità di fuga può essere calcolata eguagliando l'energia cinetica all'energia gravitazionale

(9) La quantità di energia solare che colpisce un pianeta per unità di superficie è inversamente proporzionale al quadrato della sua distanza dal sole. Se D è la distanza del pianeta dal Sole (in unità astronomiche), il flusso risulta allora pari a 1/D2 volte il flusso che colpisce la Terra (Costante solare = 1380 W/m2)

(10) Un Pianeta di raggio R posto a distanza D dal Sole intercetta una frazione di energia solare
Il rapporto tra il flusso luminoso in arrivo dal Pianeta ed il flusso in arrivo dal Sole è allora pari . Facendo ora il rapporto tra il valore effettivo e quello teorico  (calcolato nell’ipotesi che A fosse uguale ad 1) si ottiene una stima dell’albedo del pianeta

 

Fonte: http://rodomontano.altervista.org/downloads/Astronomia.zip
sito web: http://rodomontano.altervista.org/
Autore del testo: non indicato nel documento di origine

 

Astronomia appunti parte 3

 

 

Visita la nostra pagina principale

 

Astronomia appunti parte 3

 

Termini d' uso e privacy