Chimica generale 5
Chimica generale 5
Il legame covalente: Teoria dell’Orbitale Molecolare (MO)
Come abbiamo visto la teoria del Legame di Valenza descrive il legame chimico attraverso le seguenti ipotesi:
- si considerano solo gli orbitali più esterni (orbitali di valenza)
- ogni legame si forma dalla sovrapposizione di due orbitali di valenza da parte dei due atomi i quali condividono così una coppia di elettroni (gli elettroni possono anche provenire entrambi dallo stesso atomo, nel caso del legame covalente dativo)
- a seconda del tipo di sovrapposizione si formano legami di tipo σ e legami di tipo π
- le coppie di elettroni di legame sono localizzate tra i due atomi interessati dal legame e, nei casi in cui sia necessario prevedere una delocalizzazione degli elettroni su più di due atomi, si ricorre alla risonanza
- la geometria delle molecole si può prevedere con il modello VSEPR e mediante l’introduzione degli orbitali atomici ibridi
La teoria VB si trova tuttavia in difficoltà nello spiegare le proprietà magnetiche di molte molecole semplici (O2) e nel descrivere gli stati eccitati delle molecole e quindi nell’interpretare le proprietà spettroscopiche.
La teoria dell’orbitale molecolare è una teoria quantomeccanica del legame covalente che permette di descrivere lo stato di legame di molecole che la teoria VB non è in grado di giustificare. Ad esempio, la molecola dell’Ossigeno O2 risulta essere paramagnetica e ciò è compatibile solo con la presenza al suo interno di elettroni spaiati che, ne’ la teoria di Lewis, ne’ la teoria VB è in grado di giustificare.
La teoria degli orbitali molecolari considera la molecola come un insieme di nuclei e di elettroni e, valutando le loro reciproche interazioni, determina le funzioni d’onda che descrivono gli elettroni nella molecola in modo analogo a quello usato per individuare le funzioni d’onda che descrivono gli elettroni negli atomi isolati.
Gli elettroni di una molecola vengono descritti da funzioni d’onda dette orbitali molecolari le cui superfici limite si estendono su tutta la molecola. Le superfici limitedegli orbitali molecolari sono policentriche, abbracciando tutti i nuclei della molecola, a differenza di quelle degli orbitali atomici (OA) che sono monocentriche, ovvero riferite ad un solo nucleo. In altre parole tutti gli elettroni della molecola risentono dell’attrazione di tutti i nuclei e ciascun elettrone contribuisce a tenere insieme tutta la molecola.
La teoria MO prevede che, quando due atomi si legano, tutti i loro orbitali atomici (AO) di valenza si combinino per dare altrettanti orbitali molecolari (MO). La molecola più semplice è quella di H2+, costituita da un elettrone sottoposto all’azione di due protoni posti ad una certa distanza l’uno dall’altro. In questo caso si può risolvere l’equazione di Schrödinger in modo rigoroso e trovare le funzioni orbitali e i valori delle energie. In tutti gli altri casi (sistemi a più elettroni) non è possibile risolvere l’equazione d’onda ed è pertanto necessario ricorrere a metodi approssimati che tengano conto in qualche modo delle interazioni interelettroniche.
Il metodo di approssimazione più semplice e normalmente utilizzato è noto come L.C.A.O. (Linear Combination of Atomic Orbitals), in cui le funzioni d’onda degli orbitali molecolari si ottengono come combinazione lineare delle funzioni d’onda degli orbitali atomici.
Attraverso il metodo L.C.A.O. le funzioni d’onda di due orbitali atomici si combinano per somma (inteferenza costruttiva) e per sottrazione (interferenza distruttiva) generando le funzioni d’onda di altrettanti orbitali molecolari.
- L’orbitale molecolare che si genera dalla somma ha un’energia inferiore dei due orbitali atomici di partenza e manifesta un aumento della densità elettronica internucleare. E’ definito orbitale molecolare di legame ΨB. Per dare un orbitale molecolare di legame gli orbitali atomici si sovrappongono in fase (medesimo segno della funzione d’onda) e con la medesima simmetria rispetto all'asse di legame, in modo da dare interferenza costruttiva.
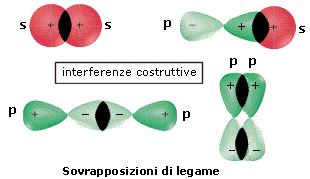
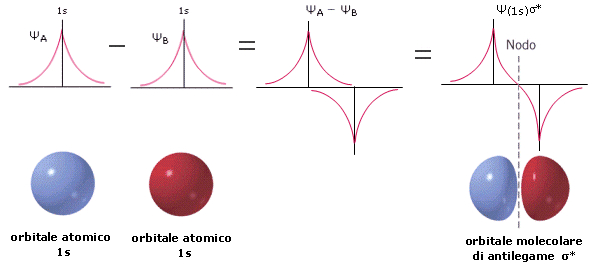
- L’orbitale molecolare che si genera dalla sottrazione ha un’energia superiore dei due orbitali atomici di partenza e manifesta un annullamento della densità elettronica internucleare (nodo). E’ definito orbitale molecolare di antilegame Ψ* in quanto, se contiene elettroni, è in grado di annullare gli effetti leganti di un orbitale di legame (contenente elettroni). La sua funzione d’onda è contrassegnata con un asterisco (*). Per dare un orbitale molecolare di antilegame gli orbitali atomici si sovrappongono con fase opposta (segno opposto della funzione d’onda) e con la medesima simmetria rispetto all'asse di legame, in modo da dare interferenza distruttiva.
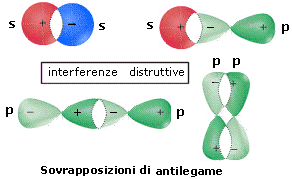
- In alcuni casi si possono generare orbitali molecolari che presentano la medesima energia degli orbitali atomici degli atomi slegati. Non avendo alcun effetto sullo stato di legame della molecola, vengono definiti orbitali molecolari di non legame ΨNB (NB = Not Bonding). La presenza di elettroni in orbitali molecolari di non legame non altera l’ordine di legame. Per dare un orbitale molecolare di non-legame gli orbitali atomici si sovrappongono con simmetria diversa rispetto all’asse di legame in modo che l’aumento di densità elettronica dovuta alla sovrapposizione delle due parti degli orbitali con segno eguale viene esattamente annullata dall’interferenza distruttiva dovuta alla sovrapposizione delle due parti degli orbitali con segno opposto.

Come avviene negli orbitali atomici, anche negli orbitali molecolari la probabilità di trovare gli elettroni è data dal quadrato della funzione d’onda Ψ2. Se, ad esempio. combiniamo due orbitali atomici con funzioni d’onda ψA e ψB, otterremo
orbitale molecolare di legame
Ψ = ψA + ψB
Ψ2 = (ψA + ψB)2 = ψA2 + ψB2 + 2ψAψB
orbitale molecolare di antilegame
Ψ* = ψA - ψB
(Ψ*)2 = (ψA - ψB)2 = ψA2 + ψB2 - 2ψAψB
Come si può osservare, la probabilità di trovare l’elettrone in un orbitale molecolare differisce dalla semplice somma delle probabilità di trovare l’elettrone nei due orbitali atomici (ψA2 + ψB2) per il termine 2ψAψB. Tale termine, detto integrale di sovrapposizione, è positivo per gli orbitali molecolari di legame (nei quali dunque la probabilità di trovare l’elettrone è maggiore rispetto agli orbitali atomici separati). è negativo per gli orbitali molecolari di antilegame (nei quali dunque la probabilità di trovare l’elettrone è minore rispetto agli orbitali atomici separati) ed è nullo per gli orbitali molecolari di non legame (nei quali dunque la probabilità di trovare l’elettrone è uguale a quella degli orbitali atomici separati).
In generale se si combinano n orbitali atomici si ottengono n orbitali molecolari, metà di legame e metà di antilegame. Quando, dalla combinazione degli orbitali atomici, si genera un numero dispari (2n+1) di orbitali molecolari, allora n sono orbitali di legame, n sono orbitali di antilegame e 1 è un orbitale di non legame.
L’energia degli orbitali molecolari è correlata al numero di nodi presenti. L’orbitale di legame a più bassa energia non presenta nodi. Maggiore è il numero dei nodi, maggiore è l’energia dell’orbitale molecolare.
Affinché due o più orbitali atomici si possano combinare linearmente fra loro per formare orbitali molecolari devono essere soddisfatti i seguenti criteri:
1. Si possono combinare solo orbitali che possiedono energie non troppo diverse tra loro.
2. Le superfici di inviluppo degli orbitali atomici devono sovrapporsi il più possibile. Se due orbitali atomici hanno un’estensione limitata ed alla distanza di legame danno una sovrapposizione trascurabile (orbitali più interni) non possono formare orbitali molecolari. In altre parole, anche per la teoria MO vale la regola generale che ai legami contribuiscono essenzialmente gli orbitali più esterni (elettroni di valenza)
3. Si possono combinare solo gli orbitali che presentano la stessa simmetria rispetto all’asse internucleare. Tipicamente una sovrapposizione asimmetrica degli orbitali genera orbitali di non legame
Una volta costruiti tutti gli orbitali molecolari, questi vengono diagrammati insieme agli orbitali atomici genitori per visualizzare l'ordine crescente dell'energia che compete loro ed infine riempiti con tutti gli elettroni degli orbitali atomici che li hanno generati, seguendo le normali regole di aufbau.
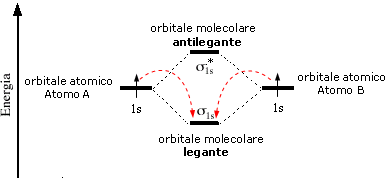
Il legame di una molecola è tanto più forte quanto maggiore è il numero di elettroni negli orbitali di legame rispetto al numero di elettroni negli orbitali di antilegame.
In generale si formerà un legame, e quindi una molecola, quando il numero di elettroni negli OM di legame (ne) supera il numero di elettroni negli OM di antilegame (ne*).
Si definisce ordine di legamela metà della differenza tra il numero degli elettroni negli orbitali di legame e il numero degli elettroni negli orbitali di antilegame (gli elettroni negli eventuali orbitali molecolari di non legame non contribuiscono).
OL = (ne - ne*)/2
Quanto più elevato è l’ordine di legame, tanto minore è la distanza internucleare e tanto maggiore è l’energia di legame.
Vediamo ad esempio il metodo MO applicato alla molecola biatomica dell’Idrogeno H2.
Se indichiamo i due atomi di Idrogeno che si legano con HA e HB, le due funzioni d’onda che si sommano e si sottraggono per dare i due orbitali molecolari sono ΨA(1s) e ΨB(1s).
Prima sommiamo le due funzioni d’onda degli orbitali atomici 1s, ottenendo la funzione d’onda dell’orbitale molecolare di legame Ψσ1s. In questo caso il valore di Ψ (e quindi anche di Ψ2) aumenta nella regione tra i due nuclei. L’aumentata densità elettronica internucleare (maggior probabilità di trovare l’elettrone) scherma le cariche positive nucleari e genera una forza attrattiva sui due nuclei che li tiene legati (OM di legame).
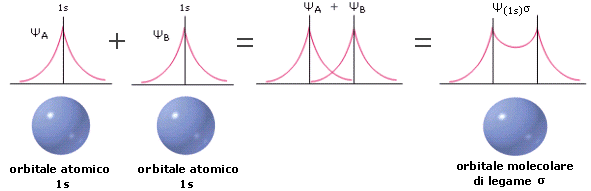
Poi sottraiamo le due funzioni d’onda degli orbitali atomici 1s, ottenendo la funzione d’onda dell’orbitale molecolare di antilegame Ψσ*1s, la quale presenta un piano nodale passante tra i due nuclei atomici. In questo caso il valore di Ψ (e quindi anche di Ψ2) diminuisce fino ad annullarsi nella regione tra i due nuclei. La diminuita densità elettronica internucleare (minor probabilità di trovare l’elettrone) non è in grado di schermare le cariche positive nucleari e di generare una forza attrattiva sui due nuclei (OM di antilegame).
Gli orbitali atomici di partenza ed i due orbitali molecolari ottenuti vengono riportati in un diagramma in funzione del loro contenuto energetico. Come abbiamo già detto l’orbitale molecolare di legame è più stabile degli orbitali atomici di partenza, mentre quello di antilegame è meno stabile. i due elettroni inizialmente presenti negli orbitali atomici di partenza si sistemano dunque nell’orbitale molecolare a più bassa energia (Principio di minima energia) con spin antiparallelo (principio di Pauli) che risulta essere l’orbitale di legame. Il diagramma suggerisce che l'energia della molecola è minore rispetto a quella associata ai due atomi isolati risultando pertanto un sistema più stabile.
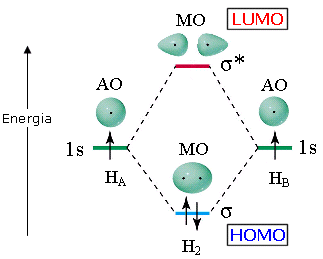
L’ultimo orbitale molecolare contenente elettroni è detto HOMO (Highest Occupied Molecular Orbital). Il primo orbitale molecolare vuoto è detto LUMO (Lowest Unoccupied Molecular Orbital). HOMO e LUMO sono definiti orbitali molecolari di frontiera.
L’andamento dell’energia potenziale per i due orbitali molecolari della molecola dell’Idrogeno in funzione della distanza interatomica è la seguente
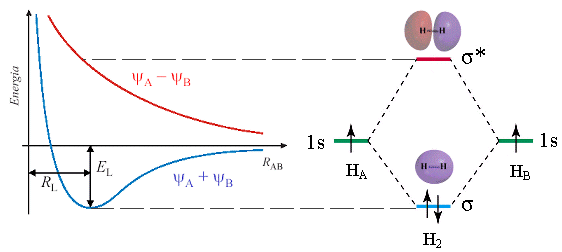
Elettroni in orbitali di legame ne = 2
Elettroni in orbitali di antilegame ne* = 0
Ordine di legame = (ne - ne*)/2 = (2 – 0) / 2 = 1.
La molecola biatomica dell’idrogeno è tenuta insieme da un legame covalente semplice.
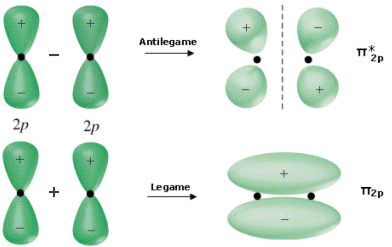
Gli orbitali p si possono combinare tra loro in due modi: frontalmente, generando orbitali molecolari σ e σ*

oppure lateralmente, generando orbitali π e π*.
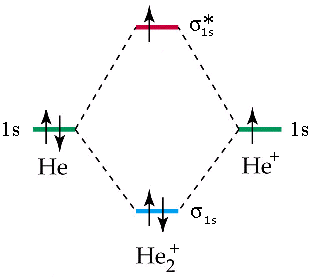
La teoria MO può spiegare perché certi composti non si formano. Se andiamo. ad esempio a diagrammare i livelli energetici della ipotetica molecola di He2, troviamo che i due elettroni nell’orbitale antilegante annullano l’effetto dei due elettroni nell’orbitale legante. L’ordine di legame è (2 – 2)/2 = 0 (nessun legame).

Mentre esiste lo ione He2+ con un ordine di legame pari a (2 – 1)/2 = 0,5
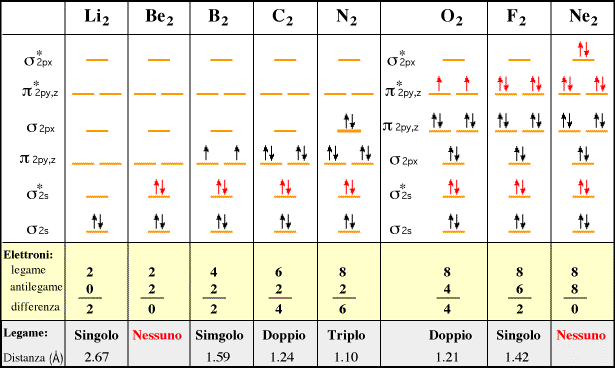
La teoria MO può spiegare le proprietà paramagnetiche della molecola dell’Ossigeno. Se andiamo a diagrammare i livelli energetici della molecola di O2, troviamo che negli orbitali antileganti a più alta energia vi sono due elettroni spaiati (regola di Hund) che giustificano il fenomeno del paramagnetismo osservato sperimentalmente e non interpretabile con la teoria VB. Le molecole paramagnetiche manifestano un momento magnetico intrinseco, ma a causa dell'agitazione termica il momento magnetico medio è nullo, tuttavia sotto l'azione di un campo magnetico esterno si verifica un fenomeno di parziale orientazione delle molecole con la comparsa di un momento magnetico risultante concorde al campo esterno (paramagnetismo).

La configurazione della molecola dell’ossigeno è
(σ2s)2 (σ2s*)2 (σ2p)2 (π2p)4 (π2p*)2
ed il suo ordine di legame è OL = ½ (2 - 2 + 2 + 4 – 2) = 2 = Legame doppio
Legame ionico
Il legame ionico è il legame che si realizza quando un atomo a bassa energia di ionizzazione si combina con un atomo ad elevata affinità elettronica. È il tipo più semplice di legame chimico ed è interpretabile in base alle leggi classiche dell’elettrostatica. Si assume un completo trasferimento di elettroni dall’atomo a bassa energia di ionizzazione all’atomo ad alta affinità elettronica. Il legame si produce come conseguenza dell’attrazione elettrostatica che si manifesta tra i due ioni di carica opposta che si formano.
Un esempio classico di legame ionico si ha nella formazione del Cloruro di Sodio a partire dal Sodio e dal Cloro elementari.
Nella reazione tra Sodio e Cloro, il Sodio metallico (configurazione superficiale 3s1) cede al Cloro (configurazione superficiale 3s23p5) il suo elettrone con formazione del Cloruro di Sodio, un composto ionico in cui gli ioni Na+ e gli ioni Cl- risultano uniti tramite legame ionico.
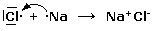
Il Sodio raggiunge in questo modo la configurazione stabile del gas nobile che lo precede (Elio), mentre il Cloro quella del gas nobile che lo segue (Argon).

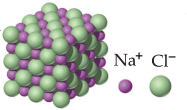
Ricordiamo tuttavia che non esiste una singola molecola di Cloruro di Sodio, come abitualmente e convenzionalmente si scrive. L'attrazione tra cariche di segno opposto, come sono cationi ed anioni, non si sviluppa infatti solo in un'unica direzione, ma agisce uniformemente in tutte le direzioni con simmetria sferica producendo aggregati ionici macroscopici strutturati in cui anioni e cationi si alternano in un reticolo ordinato. Per questo motivo il legame ionico, a differenza del legame covalente, non è direzionale.
Il numero di anioni che circonda un catione all’interno del reticolo cristallino è detto numero di coordinazione del catione.
Il numero di cationi che circonda un anione all’interno del reticolo cristallino è detto numero di coordinazione dell’anione.
Nel Cloruro di Sodio, ad esempio, ogni ione Na+ risulta circondato da 6 ioni Cl- e viceversa., formando uno sconfinato reticolato cubico, in cui ioni di carica opposta si alternano ordinatamente nelle tre direzioni dello spazio. Tale disposizione ordinata è detta cristallina, poichè genera macroscopicamente un cristallo che conserva la geometria della sottostante struttura atomica.
Nei composti ionici dunque, come abbiamo già avuto modo di dire, la formula chimica non descrive una struttura molecolare autonoma, ma indica il rapporto numerico esistente nel cristallo tra ioni positivi e negativi (formula minima). Allo stesso modo è più corretto, riferendosi ai composti ionici, parlare di peso formula piuttosto che di peso molecolare.
Nel caso del Cloruro di Sodio, ad esempio, la formula NaCl ci informa che il rapporto numerico tra ioni Na+ e Cl- all'interno del reticolo è di 1:1.
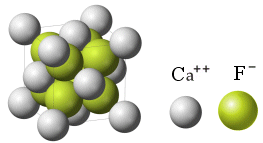
Se la reazione fosse avvenuta tra il Calcio ed il Fluoro, il Calcio avrebbe ceduto due elettroni a 2 atomi di Fluoro, ciascuno dei quali avrebbe acquistato un elettrone.
In tal caso, affinchè il reticolato ionico sia nel complesso neutro è necessario che per ciascun ione Ca2+ siano presenti 2 ioni F-.
La formula CaF2 indica dunque che nel reticolo cristallino del Fluoruro di Calcio (Fluorite) il rapporto tra ioni Calcio e ioni Fluoro è 2:1.
In un solido ionico si assume che la distanza tra gli ioni di carica opposta (distanza internucleare) sia uguale alla somma dei raggi ionici del catione e dell’anione. Le distanze internucleari possono essere misurate molto accuratamente con i metodi cristallografici, ma il problema è ovviamente stabilire quanto contribuisca il raggio di ciascun ione alla distanza totale misurata. In altre parole il problema è di assegnare a ciascun ione la sua frazione di distanza internucleare (il suo raggio ionico).
La determinazione dei raggi ionici si effettua in genere assumendo come noto il raggio ionico di uno ione e calcolando tutti gli altri per differenza.
Le prime misure di raggi ionici si devono a Pauling (1928), che assunse per lo ione ossido O2- un raggio ionico di 140 pm. L’anione O2- presenta il vantaggio di trovarsi combinato con moltissimi elementi e di essere accettabilmente non polarizzabile, per cui la sua dimensione non varia molto cambiando l’intorno.
Raggio Ionico (pm) – Pauling |
||||||||
Li+ |
Be2+ |
|
B3+ |
C |
N3- |
O2- |
F- |
|
Na+ |
Mg2+ |
Al3+ |
Si |
P3- |
S2- |
Cl- |
||
K+ |
Ca2+ |
Sc3+ |
Zn2+ |
Ga3+ |
Ge |
As3- |
Se2- |
Br- |
Rb+ |
Sr2+ |
Y3+ |
Cd2+ |
In3+ |
Sn |
Sb3- |
Te2- |
I- |
Cs+ |
Ba2+ |
La3+ |
Hg2+ |
Tl3+ |
Pb |
Bi |
Po |
At |
Successivamente Shannon e Prewitt (1969,1970) proposero valori oggi ritenuti più attendibili in cui i cationi sono significativamente più grandi e gli anioni più piccoli rispetto ai valori assegnati in precedenza.
I raggi ionici sono utili per prevedere la struttura geometrica del reticolato ionico, ma vanno usati con attenzione poiché, mescolando valori provenienti da fonti diverse, si può incorrere in grossolani errori.
Inoltre i raggi ionici non sono costanti per un certo ione, ma aumentano in genere all’aumentare del numero di ioni di carica opposta che lo circondano (numero di coordinazione). Il confronto dei raggi ionici richiede dunque l’uso di valori basati su un unico numero di coordinazione (in genere tipicamente 6).
Di seguito riportiamo i raggi ionici proposti da Shannon per il numero di coordinazione 6 (tra parentesi sono riportati eventuali numeri di coordinazione diversi)
Raggio Ionico (pm) – Shannon |
||||||||||||||||||
1 |
H+ |
|
He |
|||||||||||||||
2 |
Li+ |
Be2+ |
|
B3+ |
C4+ |
N3- |
O2- |
F- |
Ne |
|||||||||
3 |
Na+ |
Mg2+ |
|
Al3+ |
Si4+ |
P5+ |
S2- |
Cl- |
Ar |
|||||||||
4 |
K+ |
Ca2+ |
Sc3+ |
Ti4+ |
V5+ |
Cr6+ |
Mn7+ |
Fe3+ |
Co3+ |
Ni3+ |
Cu2+ |
Zn2+ |
Ga3+ |
Ge4+ |
As5+ |
Se2- |
Br- |
Kr |
5 |
Rb+ |
Sr2+ |
Y3+ |
Zr4+ |
Nb5+ |
Mo6+ |
Tc7+ |
Ru3+ |
Rh3+ |
Pd2+ |
Ag+ |
Cd2+ |
In3+ |
Sn4+ |
Sb3+ |
Te2- |
I- |
Xe |
6 |
Cs+ |
Ba2+ |
La3+ |
Hf4+ |
Ta5+ |
W6+ |
Re7+ |
Os4+ |
Ir4+ |
Pt4+ |
Au3+ |
Hg2+ |
Tl3+ |
Pb4+ |
Bi3+ |
Po4+ |
At |
Rn |
7 |
Fr+ |
Ra2+ |
Ac |
Rf |
Db |
Sg |
Bh |
Hs |
Mt |
Ds |
Rg |
Uub |
Uut |
Uuq |
Uup |
Uuh |
Uus |
Uuo |
Il numero di ioni di carica opposta che circondano un dato ione dipende da fattori geometrici secondo il principio del massimo impaccamento. In altre parole la geometria di un composto ionico è quella che rende minima l’energia del sistema, per cui ogni ione deve essere circondato dal massimo numero di ioni di segno opposto e la distanza tra ione positivo e ione negativo deve essere la minima possibile. L'impaccamento si produce come se gli ioni fossero sfere rigide che si sistemano in modo da rendere minimi gli spazi vuoti tra una sfera e l’altra (in effetti gli ioni non si comportano come sfere rigide, ma si deformano (polarizzazione) in funzione delle forze elettrostatiche di attrazione e repulsione).
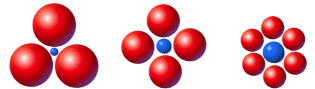
Tipi di coordinazione planare tra ioni con rapporti di raggi ionici diversi.
Il numero massimo di anioni che è possibile porre a contatto con un catione (numero di coordinazione del catione) e quindi il tipo di impaccamento e di reticolato geometrico dipende sostanzialmente dalle dimensioni relative degli ioni positivi e negativi. Più esattamente, dipende dal rapporto fra il raggio dello ione più piccolo (in genere il catione) ed il raggio dello ione più grande (in genere l’anione) o rapporto radiale (Rr = r+/r-).
Numero di |
Rapporto |
Geometria |
2 |
Rr < 0,155 |
Lineare |
3 |
0,155 ≤ Rr < 0,224 |
Trigonale |
4 |
0,225 ≤ Rr < 0.414 |
Tetraedrica |
6 |
0,414 ≤ Rr < 0,732 |
Ottaedrica |
8 |
0,733 ≤ Rr < 1 |
Cubica |
12 |
Rr = 1 |
Cubo-ottaedrica |
Ad esempio, nel Cloruro di Cesio il rapporto radiale tra il raggio ionico di Cs+ e quello di Cl- vale rCs+/rCl- = 167/181 = 0,923. Il cesio presenterà dunque un numero di coordinazione NC = 8 ed una geometria cubica
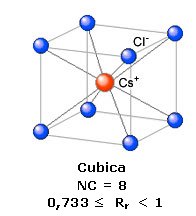
Ogni ione Cs+ è circondato da 8 ioni Cl- e, poiché il rapporto ionico e 1:1, anche ogni ione Cl- sarà circondato da 8 ioni Cs+
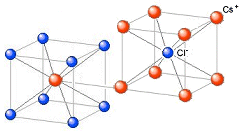
Nel Fluoruro di Calcio (CaF2 Fluorite) il rapporto radiale tra il raggio ionico di Ca2+ e quello di F- vale rCa2+/rF- = 100/133 = 0,75. Il Ca2+ presenterà dunque un numero di coordinazione NC = 8 ed una geometria cubica a facce centrate.
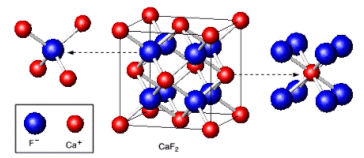
Ogni ione Ca2+ è circondato da 8 ioni F- disposti al vertice di un ottaedro. Ma, poiché il rapporto ionico e 1:2, ogni ione F- sarà circondato da 4 ioni Ca2+ disposti ai vertici di un tetraedro
Nel Cloruro di Sodio (NaCl) il rapporto radiale tra il raggio ionico di Na+ e quello di Cl- vale rCa+/rCl- = 102/181 = 0,56. Il Na+ presenterà dunque un numero di coordinazione NC = 6 ed una geometria ottaedrica.
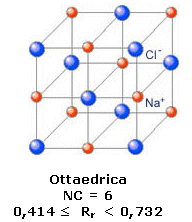
Ogni ione Na+ è circondato da 6 ioni Cl- disposti al vertice di un ottaedro e, poiché il rapporto ionico e 1:1, anche ogni ione Cl- sarà circondato da 6 ioni Na+ disposti al vertice di un ottaedro
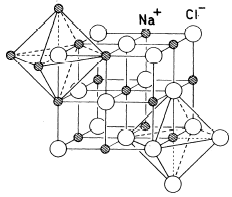
Per sapere perché le sostanze ioniche formino cristalli e non si limitino a costituire coppie ioniche isolate, occorre fare alcune considerazioni energetiche sui legami ionici.
Consideriamo allora il legame ionico dal punto di vista energetico, analizzando ancora una volta la reazione di sintesi del Cloruro di Sodio.
2Na(s) + Cl2(g) → 2 NaCl(s) + 196,6 kcal
L'energia che si libera durante la formazione del legame è pari a 96,3 kcal per mole di NaCl (Entalpia di formazione ΔHf = -96,3 kcal/mol). Evidentemente trasformandosi in ioni entrambi gli atomi hanno raggiunto una configurazione più stabile ed hanno diminuito il loro contenuto energetico.
Tuttavia se confrontiamo semplicemente le variazioni di energia associate alla formazione degli ioni, il processo non sembra energeticamente favorito.
Il Sodio presenta una energia di ionizzazione molto bassa
Na(g) + 118,5 kcal/mol → Na+(g) + e-
mentre il Cloro ha una Affinità elettronica molto elevata
Cl(g) + e- → Cl-(g) + 83,4 kcal/mol
In effetti, sommando l’Energia di ionizzazione del Sodio e l’energia di Affinità elettronica del Cloro, il processo di formazione del legame ionico non sembrerebbe favorito, richiedendo 35,1 kcal
Na(g) + 118,5 kcal → Na+(g) + e- +
Cl(g) + e- → Cl-(g) + 83,4 kcal =

Na(g) + Cl(g) + 35,1 kcal → Na+(g) + Cl-(g)
Il fatto è che la reazione precedente non descrive la formazione del cloruro di sodio, ma quella dei suoi ioni allo stato gassoso, idealmente posti a distanza infinita l’uno dall’altro. Il processo di avvicinamento degli ioni, sotto l’azione delle reciproche forze di attrazione, fino a formare il composto ionico fa notevolmente diminuire l’energia del sistema.
Si definisce energia reticolare l’energia liberata nella formazione del reticolo cristallino dagli ioni componenti allo stato gassoso portati da distanza infinita a distanza di legame.
L’energia reticolare dipende da diversi fattori, ma in particolare dalla densità di carica (q/r = rapporto carica/raggio). Più elevata è la densità di carica maggiore è l’energia reticolare.
|
|
Li+ |
Na+ |
K+ |
Rb+ |
Cs+ |
|
Be2+ |
Mg2+ |
Ca2+ |
Sr2+ |
Ba2+ |
|
q/r |
1,32 |
0,98 |
0,72 |
0,60 |
0,56 |
|
4,44 |
2,78 |
2,00 |
1,69 |
1,48 |
F- |
0.75 |
1036 |
923 |
821 |
785 |
740 |
|
3505 |
2957 |
2630 |
2492 |
2352 |
Cl- |
0.55 |
853 |
786 |
715 |
689 |
659 |
|
3020 |
2526 |
2258 |
2156 |
2056 |
Br- |
0,51 |
807 |
747 |
682 |
660 |
631 |
|
2914 |
2440 |
2176 |
2075 |
1985 |
I- |
0,45 |
757 |
704 |
649 |
630 |
604 |
|
2800 |
2327 |
2074 |
1963 |
1877 |
Densità di carica (q/r) ed energia reticolare (kJ mol-1) misurata e calcolata (tra parentesi)
per gli alogenuri dei metalli alcalini ed alcalino-terrosi
Tuttavia va tenuto presente che se il catione è troppo piccolo (densità di carica eccessivamente elevata) esso non riesce ad inserirsi efficacemente nel reticolo cristallino poiché gli anioni verrebbero a contatto, e tenderà pertanto a stabilizzarsi tramite legami covalenti. Così ad esempio gli elementi del II gruppo formano tutti composti ionici ad eccezione del Be2+ (troppo piccolo). Così non sono noti composti ionici del B3+ e del C4+.
L’energia reticolare risulta essenzialmente data dalla combinazione di due termini opposti la repulsione tra i gusci elettronici (energia di repulsione elettronica) e l’attrazione tra ioni di carica opposta (energia di Madelung).
Quando idealmente gli ioni di carica opposta si avvicinano, l’energia reticolare diminuisce fino ad arrivare ad un valore minimo per una distanza tra gli ioni pari alla somma dei loro raggi ionici.
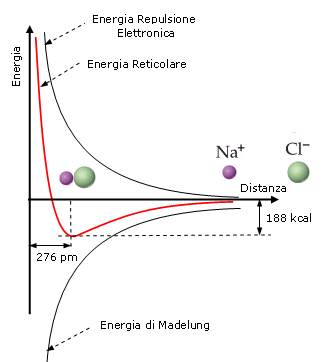
Nel caso del Cloruro di Sodio, ad esempio, l’energia reticolare è pari a 188 kcal/mol in corrispondenza ad una distanza interionica di 276 pm (picometri) = 181 pm (raggio ionico Cl-) + 95 pm (raggio ionico Na+).
Per valutare l’entità dell’energia reticolare di un cristallo di Cloruro di Sodio, iniziamo a calcolare l’energia potenziale coulombiana di una coppia ionica gassosa di NaCl. Studiando la molecola di cloruro di sodio biatomica gassosa, si è trovato che la sua distanza internucleare è 2,38 Å, per cui l’energia potenziale coulombiana è
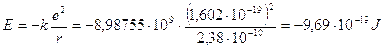
per ottenere l’energia di una mole di coppie ioniche è necessario moltiplicare il risultato precedente per il numero di Avogadro
-9,69·10-19 x 6.022·1023 = -583,6 kJ mol-1 = -139,6 kcal mol-1
Ora, per trovare l’energia di formazione sviluppata quando un cristallo di cloruro di sodio si forma dagli ioni gassosi, si deve calcolare l’energia potenziale coulombiana di uno ione quando esso è sotto l’azione di tutti gli altri ioni del cristallo. A tal fine consideriamo il modello semplificato monodimensionale seguente e calcoliamo l’energia coulombiana degli ioni rispetto allo ione sodio centrale
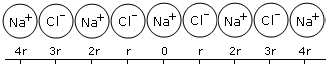
I primi due ioni di cloro vicini, disposti ad una distanza r, contribuiranno all’energia potenziale con un valore pari a -2ke2/r , mentre i successivi due ioni sodio contribuiranno con +2ke2/2r (il segno positivo deriva dalla repulsione tra le cariche eguali sugli ioni di sodio).
Continuando il ragionamento si ha:
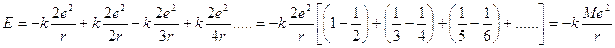
Come si può osservare, l’espressione dell'energia totale è data da uno sviluppo in serie in cui il valore di ogni addendo dipende dalla carica degli ioni che interagiscono e dalla posizione che questi occupano nel reticolo, mentre è indipendente dalla natura chimica degli ioni che effettivamente occupano le posizioni.
Lo sviluppo in serie è costituito da una sequenza di addendi alternativamente negativi e positivi ma di entità sempre più piccola, che converge verso un valore numerico M maggiore di 1, detto Costante di Madelung, indipendente dal valore di r.
La costante di Madelung dipende dunque solo dal tipo di reticolo e dalla mutua posizione geometrica dei singoli ioni.
Esempio |
Numero di coordinazione dei cationi |
Numero di coordinazione degli anioni |
Costante di Madelung |
NaCl |
6 |
6 |
1,7475 |
CsCl |
8 |
8 |
1,7627 |
ZnS (wurtzite) |
4 |
4 |
1,6413 |
ZnS (blenda) |
4 |
4 |
1,6381 |
CaF2 (fluorite) |
8 |
4 |
2,5194 |
TiO2 (rutilo) |
6 |
3 |
2,4080 |
Poiché la costante di Madelung è sempre maggiore di uno, l’energia di attrazione elettrostatica globale è di conseguenza sempre maggiore (in valore assoluto) nel reticolo rispetto al caso di una singola coppia ionica.
Questa energia, che si ottiene moltiplicando l'energia di interazione della coppia per la costante di Madelung relativa, con le debite correzioni, si chiama Energia di Madelung, principale responsabile della stabilità dei cristalli delle sostanze ioniche. Se essa non ci fosse, esisterebbero solo coppie ioniche isolate.
Per il reticolo cristallino del cloruro di sodio è M = 1,75, per cui, a parità di tutte le altre condizioni, il solido ionico ha un’energia che è il 75% più bassa di quella della molecola biatomica gassosa. Questo ulteriore abbassamento di energia si verifica perché uno ione sodio nel solido è legato mediante forze coulombiane a tutti gli ioni nel cristallo.
Essendo la distanza tra gli ioni nel cristallo del cloruro di sodio pari a 2,76 Å (maggiore che nella molecola biatomica) si ha
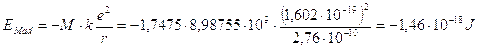
per ottenere l’energia di Madelung di una mole è necessario moltiplicare il risultato precedente per il numero di Avogadro
-1,46·10-18 x 6.022·1023 = -879,5 kJ mol-1 = -210,4 kcal mol-1
Per calcolare l’energia reticolare è ora necessario stimare anche l’energia repulsiva che si genera tra le nuvole elettroniche degli ioni quando questi si trovano a piccole distanze.
Eret = EMad + Erep
Tale repulsione è della stessa natura delle repulsioni di van der Waals fra gli atomi neutri di cui ci occuperemo nel prossimo capitolo ed ha una dipendenza dalla distanza interatomica r del tipo
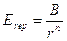
con
n > 6 (con valori caratteristici 9, 12 o 14 in relazione al tipo di ioni. Spesso n può essere calcolato studiando la compressibilità del cristallo)
B = coefficiente caratteristico del solido ionico
L’espressione dell’energia reticolare diventa dunque
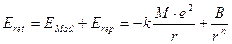
Tuttavia B può essere eliminato dall’espressione dell’energia reticolare considerando che al valore di r in cui il cristallo è più stabile (r di legame) l’energia reticolare assume il suo valore minimo (pendenza nulla e derivata della funzione uguale a zero dE/dr=0).
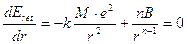
da cui
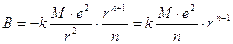
che, sostituita nella relazione dell’Energia reticolare, fornisce
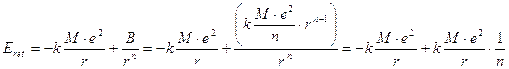
Dunque, poiché n » 10, l’energia di repulsione risulta circa 1/10 dell’energia di Madelung e quindi, per il cloruro di sodio
Eret = EMad + Erep = -210,4 + 21,04 = 189 kcal mol-1
Il valore sperimentale dell’energia reticolare per NaCl è di 188 kcal mol-1
L’energia reticolare può essere sperimentalmente determinata tramite un ciclo di Born-Haber, in cui il processo di formazione del legame ionico viene spezzato in una serie di fasi che trasformano i reagenti negli ioni gassosi e successivamente gli ioni gassosi nel solido ionico.
1) Vaporizzazione del Sodio (Energia di vaporizzazione)
Na(s) + ½ Cl2(g) + 26 kcal → Na(g) + ½ Cl2(g)
2) Dissociazione del Cloro (½ dell’energia di legame Cl-Cl)
Na(g) + ½ Cl-Cl(g) + 28,6 kcal → Na(g) + Cl•(g)
3) Ionizzazione del Sodio (Energia di Ionizzazione)
Na(g) + Cl•(g) + 118,5 kcal → Na+(g) + Cl•(g) + e
4) Ionizzazione del Cloro (Energia di Affinità elettronica)
Na+(g) + Cl•(g) + e → Na+(g) + Cl+(g) + 83.4 kcal
5) Formazione legame a partire dagli elementi gassosi (Energia reticolare)
Na+(g) + Cl+ (g) → NaCl(s) + 188 kcal
Sommando membro a membro le 5 reazioni precedenti si ottiene la reazione di formazione del Cloruro di Sodio a partire dai suoi elementi e la relativa Energia di formazione
Na(s) + ½ Cl2(g) → NaCl(s) + 98,3 kcal
I diversi stadi vengono spesso schematicamente rappresentati attraverso il cosiddetto ciclo di Born-Haber, dove, secondo la convenzione, le energie assorbite hanno segno positivo, quelle cedute segno negativo
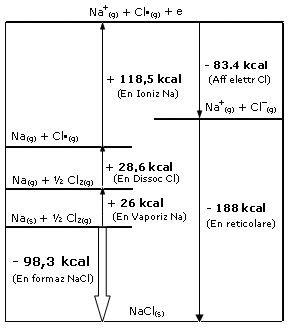
Come si può osservare, nella formazione di sostanze ioniche è particolarmente importante il confronto tra l’energia di ionizzazione e l’energia reticolare, trattandosi dei due termini energetici più rilevanti. In prima approssimazione un composto ionico si formerà se l’energia spesa per la ionizzazione verrà compensata dall’energia reticolare. Ad esempio, il composto ionico MgCl con Mg+ non si osserva, nonostante lo ione Mg+ richieda meno energia per formarsi rispetto allo ione Mg2+ (Mg = Mg+ + e + 738 kJ mol-1 contro Mg+ = Mg2+ + e + 1450 kj mol-1). Ciò è dovuto al fatto che l’energia reticolare di MgCl è troppo piccola.
Legame metallico
Il legame che tiene uniti gli atomi metallici all'interno del solido è detto legame metallico.
Tra i modelli più semplici ed intuitivi che descrivono il legame metallico vi è quello di P.Drude (1863-1906), secondo il quale gli atomi metallici perdono facilmente gli elettroni superficiali trasformandosi in ioni positivi. Gli ioni si accatastano in modo da lasciare il minor spazio vuoto possibile (massimo impaccamento), andando così ad occupare posizioni ben determinate all'interno di precise strutture geometriche. Gli elettroni persi non appartengono più ai singoli atomi, ma a tutto il reticolo solido (modello a mare di elettroni). Essi sono liberi di muoversi (elettroni delocalizzati) tra gli ioni positivi garantendo la neutralità del sistema e agendo da collante per i cationi.
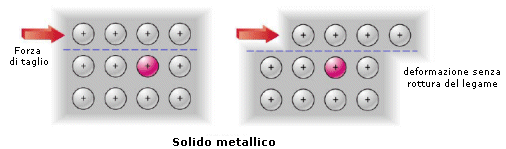
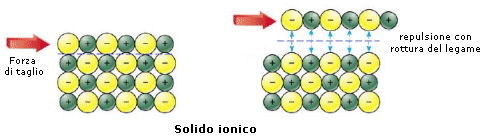
La libertà di movimento degli elettroni all’interno del reticolato cationico fa sì che il legame metallico manifesti una natura non direzionale. Non vi sono elettroni localizzati, come nel legame covalente, che irrigidiscono la struttura. Gli stessi cationi possono, se sollecitati meccanicamente, muoversi all’interno del mare di elettroni senza che il legame venga spezzato, a differenza di quanto accade in un legame ionico in cui anioni e catoni devono mantenere le loro posizioni reciproche. .Il legame metallico è adirezionale. Ciò spiega le caratteristiche di duttilità e malleabilità dei metalli i quali, se sottoposti a sollecitazioni meccaniche, si deformano in modo permanente senza spezzarsi.
Se ad esempio sottoponiamo un solido metallico ed un solido ionico ad una forza di taglio che faccia slittare reciprocamente un piano di atomi rispetto ad un altro, possiamo notare che:
- il legame metallico si conserva. La posizione che assumono i cationi nel mare di elettroni è infatti indifferente rispetto all’efficacia del legame
- il legame ionico viene spezzato. Anioni e cationi vengono infatti a trovarsi di fronte a cariche dello stesso segno e si respingono.
Questo modello di legame giustifica una struttura costituita da un denso reticolato di ioni positivi molto vicini tra loro secondo il principio del massimo impaccamento. Il numero di atomi adiacenti a ciascun atomo è detto numero di coordinazione (N.C.) e per i metalli è molto elevato, tipicamente 8 o 12. Per questo motivo la densità dei metalli è generalmente superiore a quella degli altri materiali.
La disposizione degli atomi metallici all’interno del reticolo cristallino può essere di tipo compatto o di tipo non-compatto.
Le disposizioni di tipo compatto sono le più frequenti (90%) e si basano su stratificazioni di atomi con distribuzione esagonale.

distribuzione esagonale
Vanno a formare reticoli cristallini con elevato numero di coordinazione (12):
- reticolo cubico a facce centrate (CFC)
- reticolo esagonale compatto (EC).
Le disposizioni di tipo non-compatto si basano su stratificazioni di atomi con distribuzione quadrata.

distribuzione quadrata
Vanno a formare reticoli cristallini con numero di coordinazione inferiore:
- reticolo cubico semplice (CS) o cubico primitivo (CP) con numero di coordinazione 6
- reticolo cubico a corpo centrato (CCC) con numero di coordinazione 8
I diversi reticoli cristallini vengono descritti mediante l’individuazione di un elemento geometrico di base, detto cella elementare o cella unitaria, che si ripete al loro interno.
In un modello a sfere rigide lo spazio occupato dagli atomi all’interno di un reticolato cristallino viene misurato dal fattore di compattazione atomica o coefficiente di impaccamento definito dal rapporto tra il volume degli atomi contenuti in una cella unitaria del reticolo ed il volume della cella.
Reticolo Cubico Semplice o Cubico Primitivo – CS (sc – simple cubic packing)
La cella unitaria è costituita da otto atomi ai vertici di un cubo.
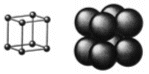
Ciascuno degli 8 atomi che si trovano ai vertici della cella è però condiviso da altre sette celle e appartiene quindi a ciascuna di esse per 1/8. In totale ogni cella contiene quindi un numero di atomi equivalenti pari a 8·1/8 = 1.
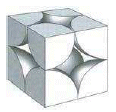
La distribuzione avviene per strati di sfere con disposizione quadrata. Le sfere del secondo strato giacciono esattamente sopra le sfere del primo strato. In questo modo ciascuna sfera è in contatto con altre sei sfere ed il numero di coordinazione è 6.
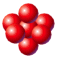
Si tratta di un reticolo estremamente raro nei metalli che compare solo nel Polonio.
Lo spigolo della cella elementare è detto costante reticolare a (o parametro di cella).
La distanza tra due atomi in contatto corriponde a 2r (due volte il raggio atomico) ed è uguale in questo caso al parametro di cella a. Poiché infatti vi sono 2 atomi a contatto lungo un lato della cella cubica, la costante reticolare è pari a 2 volte il raggio atomico
a = 2r
Il volume della cella elementare in funzione del raggio atomico r è quindi
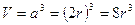
Il coefficiente di impaccamento (fattore di compattazione atomica) si ottiene come rapporto tra il volume degli atomi equivalenti (sfere contenute nella cella elementare, in questo caso 1) ed il volume della cella elementare.
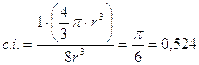
Reticolo |
|
Esempi |
Po |
Numero di atomi per cella elementare |
1 |
Numero di coordinazione |
6 |
Distanza tra atomi più vicini |
a |
Coefficiente di impaccamento |
p / 6 = 0,524 = 52,4% |
Dimensione della cella (costante reticolare a) |
2r |
Reticolo Cubico a Corpo Centrato – CCC (bcc - body centered cubic)
La cella unitaria è costituita da un atomo al centro di essa e da otto atomi ai vertici.
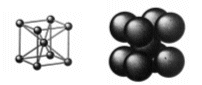
In questo modo gli atomi ai vertici non sono in contatto tra loro. Viceversa sono in contatto gli atomi sulla diagonale del corpo della cella nella sequenza “vertice-centro cella-vertice”.
L’atomo centrale è dunque in contatto con 8 sfere ed il numero di coordinazione è 8
Ciascuno degli 8 atomi che si trovano ai vertici della cella è però condiviso da altre sette celle e appartiene quindi a ciascuna di esse per 1/8. In totale ogni cella contiene quindi un numero di atomi equivalenti pari a 1 + 8·1/8 = 2.
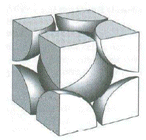
La distribuzione avviene per strati di sfere con disposizione quadrata. Le sfere del secondo strato giacciono nelle depressioni create dal primo strato, mentre le sfere del terzo strato giacciono nelle depressioni create dal secondo strato in modo da trovarsi esattamente sopra le sfere del primo strato
Lo spigolo della cella elementare è detto costante reticolare a.
Poiché vi sono 3 atomi a contatto lungo la diagonale D della cella cubica, la diagonale è pari a 4 volte il raggio atomico
D = 4r
Ricordando che in un cubo la diagonale è pari
D = a Ö3
con a = spigolo del cubo, la relazione tra il raggio atomico r e la costante reticolare a diventa
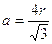
La minima distanza tra due atomi (2r) vale quindi (a · Ö3) / 2 = 0,866 a
Il volume della cella elementare in funzione del raggio atomico r è
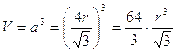
Il coefficiente di impaccamento (fattore di compattazione atomica) si ottiene come rapporto tra il volume degli atomi equivalenti (sfere contenute nella cella elementare, in questo caso 2) ed il volume della cella elementare.
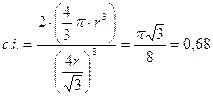
Reticolo |
|
Esempi |
Fe-a (a = 2,861Å), |
Numero di atomi per cella elementare |
2 |
Numero di coordinazione |
8 |
Distanza tra atomi più vicini |
a · Ö3 / 2 = 0,866 · a |
Coefficiente di impaccamento |
Ö3 · p / 8 = 0,68 = 68% |
Dimensione della cella (costante reticolare a) |
(4/Ö3)r |
Esempio
Il tungsteno (W) presenta una struttura cubica a corpo centrato. Calcoliamo la sua densità sapendo che il suo raggio atomico è 137 pm ed il suo peso molare è 183,84 g/mol
La densità del tungsteno può essere calcolata come rapporto tra la massa degli atomi contenuti in una cella ed il volume della cella. In una cella cubica a corpo centrato sono contenuti 2 atomi la cui massa è pari a
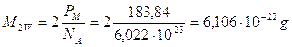
Per una cella cubica a corpo centrato la relazione tra le dimensioni dello spigolo a della cella ed il raggio r dell’elemento è
a = r (4/Ö3) = 1,37 10-8 x ((4/Ö3) = 3,164 10-8 cm
ed il volume della cella sarà
Vcella = a3 = (3,164 10-8)3 = 3.167 10-23 cm3.
La densità del Tungsteno sarà dunque
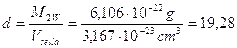 g/cm3
g/cm3
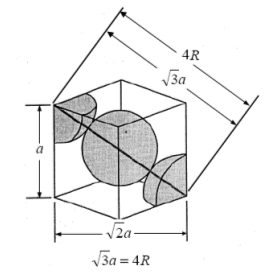
Reticolo Cubico a Facce Centrate – CFC (fcc - face centered cubic)
Detto anche cubico compatto (CC). Nessun atomo giace interamente all'interno della cella unitaria ma vi sono 8 atomi ai vertici e 6 atomi al centro di ognuna delle facce.
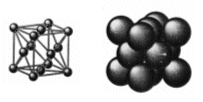
Così che ciascun atomo delle 6 facce è condiviso anche da un'altra cella e conta per 1/2 (contenuto in atomi = 6 x 1/2 = 3), mentre gli otto atomi ai vertici, come nella cella CCC, contano per 1/8 (8 x 1/8 = 1) Quindi in totale vi sono 4 atomi equivalenti per cella.
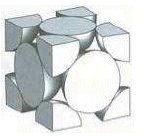
In questa cella gli atomi lungo la diagonale del cubo non sono in contatto tra loro. Viceversa sono in contatto gli atomi lungo la diagonale delle facce nella sequenza “vertice-centro faccia-vertice”.
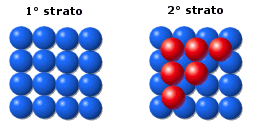
La distribuzione avviene per strati sovrapposti di sfere con disposizione esagonale. Le sfere del secondo strato giacciono nelle depressioni create dal primo strato, mentre le sfere del terzo strato giacciono nelle depressioni create dal secondo strato, non sopra le sfere del primo strato, ma in corrispondenza delle depressioni del primo strato non occupate dalle sfere del secondo strato.
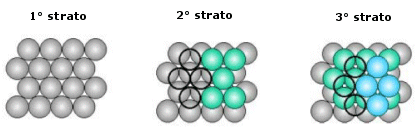
Solo le sfere del quarto stato si posizionano nelle depressioni del terzo in modo da sovrapporsi esattamente alle sfere del primo strato. Ne deriva una successione di strati esagonali di tipo ABCA..
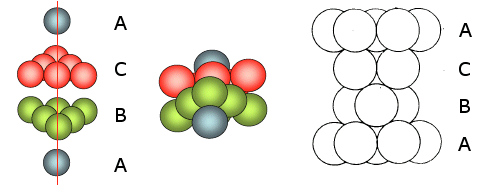
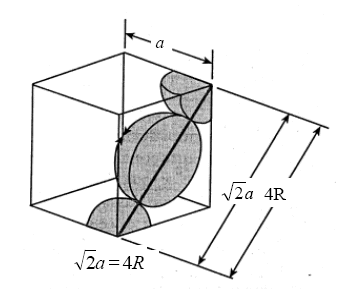
In questa cella sono in contatto 3 atomi lungo la diagonale DF della faccia del cubo,
DF = 4r
Ricordando che in un cubo la diagonale di una faccia è pari
DF = a Ö2
con a = spigolo del cubo, la relazione tra il raggio atomico r e la costante reticolare a diventa
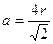
La minima distanza tra due atomi (2r) vale quindi (a · Ö2) / 2 = 0,707 a
Il volume della cella elementare in funzione del raggio atomico r è
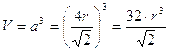
Il coefficiente di impaccamento (fattore di compattazione atomica) si ottiene come rapporto tra il volume degli atomi equivalenti (sfere contenute nella cella elementare, in questo caso 4) ed il volume della cella elementare.
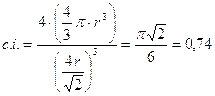
Il numero di coordinazione è il massimo raggiungibile con atomi dello stesso raggio e vale 12. La percentuale di spazio occupata è la più grande possibile in una struttura cristallina ad arriva al 74%, eguagliata soltanto da quella ottenibile nell’impaccamento esagonale compatto, come quello del titanio metallico.
Reticolo cubico a facce centrate |
|
Esempi |
Fe-g (a = 3,601), |
Numero di atomi per cella elementare |
4 |
Numero di coordinazione |
12 |
Distanza tra atomi più vicini |
a · Ö2 / 2 = 0,707 · a |
Coefficiente di impaccamento |
Ö2 · p / 6 = 0,74 = 74% |
Dimensione della cella (costante reticolare a) |
(4/Ö2)r |
fonte: http://www.pianetachimica.it/didattica/documenti/Chimica_Generale.doc
Chimica generale 5
Visita la nostra pagina principale
Chimica generale 5
Termini d' uso e privacy
