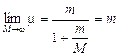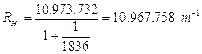Chimica appunti parte 2
Chimica appunti parte 2
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Modelli atomici quantistici semiclassici
Come abbiamo già avuto modo di dire il modello planetario di Rutherford risultava in contraddizione con i principi dell'elettrodinamica classica e doveva pertanto essere corretto. Rimaneva inoltre ancora irrisolto il problema degli spettri a righe, la cui soluzione appariva con molta probabilità legata proprio alla struttura atomica.
Visto il successo ottenuto nella risoluzione del problema del corpo nero e dell'effetto fotoelettrico, attraverso l'introduzione nel formalismo matematico della costante di Planck, Bohr decise di tentare la stessa strada anche per risolvere il problema degli spettri a righe.
Il modello atomico di Bohr
Preso in considerazione l'atomo di Idrogeno, Bohr introdusse alcune ipotesi in modo da far intervenire all'interno della struttura atomica la costante h.
1a ipotesi |
Esiste uno stato stazionario dell'atomo caratterizzato da particolari orbite circolari lungo le quali gli elettroni si muovono senza emettere radiazioni elettromagnetiche. Gli elettroni che percorrono tali orbite stazionarie possiedono una certa quantità ben definita di energia detta livello energetico dell'orbita.
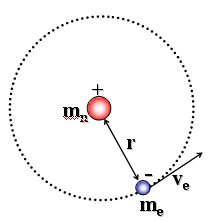
Essendo gli elettroni in equilibrio in tali orbite la forza centrifuga (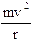 Per l’Idrogeno Z = 1 e la relazione diventa
Per l’Idrogeno Z = 1 e la relazione diventa
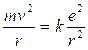
da cui si ricava il raggio
1) 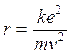
2a ipotesi |
A questo punto Bohr impose, del tutto arbitrariamente una condizione di quantizzazione. Tra le infinite orbite che soddisfano la 1) sono permesse solo quelle che soddisfano la seguente relazione
2) 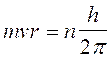
dove mvr è il momento della quantità di moto dell'elettrone in orbita attorno al suo nucleo, detto anche momento angolare orbitale. h/2p prende il nome di costante di Planck normalizzata e viene spesso indicata con 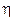 (acca tagliato) ed n è un numero intero positivo, detto numero quantico principale. In pratica Bohr impone una condizione di quantizzazione del momento angolare, che si rivelerà in seguito fondamentale e caratteristica di qualsiasi corpo rotante.
(acca tagliato) ed n è un numero intero positivo, detto numero quantico principale. In pratica Bohr impone una condizione di quantizzazione del momento angolare, che si rivelerà in seguito fondamentale e caratteristica di qualsiasi corpo rotante.
Tale condizione si esprime dicendo che il momento angolare dell'elettrone deve essere un multiplo intero di acca tagliato.
Il momento angolare quantizzato condiziona i valori che possono assumere il raggio delle orbite e l’energia totale (cinetica + potenziale) o livello energetico, che l’elettrone possiede.
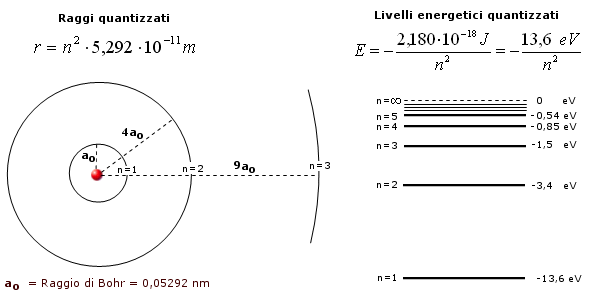
Raggi e livelli energetici risultano pertanto anch’essi quantizzati in funzione di n.
Raggio quantizzato: Dalla condizione di quantizzazione del momento angolare si ricava la velocità che sostituita nella 1) fornisce la relazione quantistica del raggio
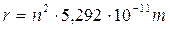
per n = 1
r = 5,292 10-11 m (= 52,92 pm = 0,5292 Å) è il raggio della orbita circolare più vicina al nucleo dell’Idrogeno ed è detto raggio di Bohr (ao) .
In fisica atomica il raggio di Bohr ao viene utilizzato come unità di misura di lunghezza e denominato bohr.
1 bohr = 5,291772 10-11 m
Energia quantizzata (livello energetico): L’energia associata ad un elettrone in moto su di un’orbita quantizzata si calcola come somma dell’energia cinetica (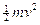 e la sostituiamo nell’espressione dell’energia cinetica, l’energia totale vale
e la sostituiamo nell’espressione dell’energia cinetica, l’energia totale vale
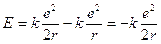
Sostituendo r con il valore quantizzato del raggio si ottiene
Il valore negativo dell'energia deriva dalla convenzione di porre pari a zero l'energia potenziale dell'elettrone a distanza infinita.
Per n = 1 l’elettrone si trova nello stato di minima energia possibile, detto stato fondamentale. Gli stati caratterizzati da n > 1 si dicono stati eccitati.
In fisica atomica l’energia potenziale coulombiana dell’elettrone nella prima orbita di Bohr viene utilizzata come unità di misura di energia e denominata hartree (in onore del fisico inglese Douglas Rayner Hartree).
.
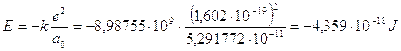
1 hartree = 4,359 10-18 J
Un hartree corrisponde al doppio dell'energia di legame dell'elettrone nello stato fondamentale (n = 1) dell'atomo di idrogeno
3^ Ipotesi |
L'atomo può passare dallo stato fondamentale ad uno eccitato assorbendo energia. In questo modo gli elettroni possono assumere l'energia necessaria per passare da un'orbita più interna ad una più esterna. L'energia assorbita affinché avvenga il salto quantico dell'elettrone, o transizione elettronica, deve essere esattamente uguale alla differenza di energia esistente tra il livello energetico superiore e quello inferiore.

Quando l'elettrone si trova in un orbita superiore a quella in cui si trova normalmente, l'atomo possiede un surplus di energia che lo rende instabile (eccitato). L'elettrone è quindi destinato a tornare nell'orbita di partenza riemettendo l'energia precedentemente assorbita tramite un fotone la cui energia è appunto pari a
E2 – E1 = DE = hn
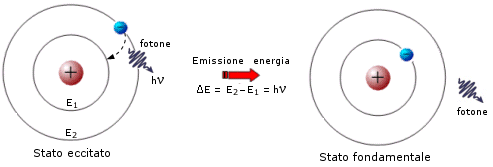
La radiazione emessa, avendo una frequenza univocamente determinata dalla differenza di energia esistente tra due particolari livelli energetici, è rigorosamente monocromatica ed apparirà come una ben determinata riga allo spettroscopio.
L’energia emessa durante una transizione da un livello n2 ad un livello n1, con n2 > n1, è
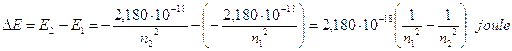
Ricordando che DE = hn e che c = ln, sostituendo opportunamente si ottiene 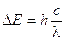 ed in definitiva
ed in definitiva
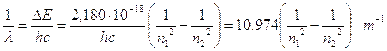
Per calcolare il numero d’onde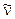
I numeri interi n ed m che nella relazione di Balmer non presentavano alcun significato fisico, nel modello atomico di Bohr diventano rispettivamente il numero quantico del livello più interno n1 ed il numero quantico del livello più esterno n2, tra i quali avviene la transizione.
- Ponendo nella n1 = 2 ed n2 intero superiore a due si possono trovare tutte le lunghezze d'onda delle righe spettrali prodotte dalle transizioni elettroniche dalle orbite più esterne verso la seconda orbita. Tale righe spettrali corrispondono ovviamente alla serie di Balmer.
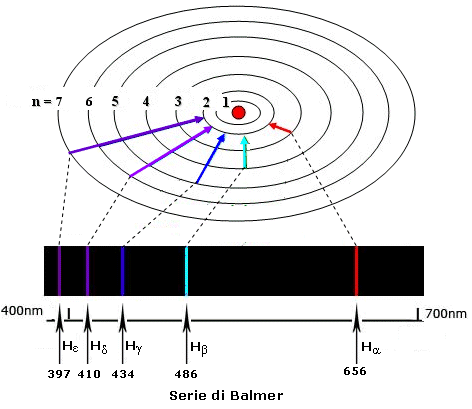
- Ponendo invece n1 = 1 si ottengono le righe spettrali della serie di Lyman, le quali rappresentano dunque le transizioni elettroniche dalle orbite più esterne verso la prima e così via per le altre serie
- Ponendo infine n2 = ¥ si ottiene la lunghezza d’onda che deve possedere la luce con cui irraggiare l'atomo per estrarre l'elettrone e portarlo all'infinito. In altri termini è possibile calcolare teoricamente l'energia di ionizzazione dell'atomo.
Il numero quantico principale n può assumere teoricamente tutti i valori compresi tra 1 ed infinito. In pratica però tutti gli atomi conosciuti sistemano i loro elettroni al massimo in 7 livelli energetici, i quali vengono spesso indicati con le lettere K, L, M, N, O, P, Q.
Righe spettrali (λ in nm) |
||||||||||
|
|
n esterno |
||||||||
Serie |
n interno |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
∞ |
Lyman |
1 |
121,6 |
102,5 |
97,2 |
94,9 |
93,7 |
93,0 |
92,6 |
92,3 |
91,15 |
Balmer |
2 |
|
656.3 |
486.1 |
434.1 |
410.2 |
397.0 |
388.9 |
383.5 |
364.6 |
Paschen |
3 |
|
|
1874.5 |
1281.4 |
1093.5 |
1004.6 |
954.3 |
922.6 |
820.1 |
Brackett |
4 |
|
|
|
4052.5 |
2625.9 |
2166.1 |
1945.1 |
1818.1 |
1458.0 |
Pfund |
5 |
|
|
|
|
7476 |
4664 |
3749 |
3304 |
2279 |
Un altro aspetto notevole del modello di Bohr è che la costante di Rydberg viene ad essere calcolata in funzione di costanti note (come la carica dell’elettrone, la sua massa, la velocità della luce, etc) ed il suo valore risulta in ottimo accordo con il valore misurato sperimentalmente
Costante di Rydberg |
Calcoliamo a titolo d’esempio il dislivello energetico esistente tra n = 2 ed n = 3, la frequenza e la lunghezza d'onda della riga spettrale (Ha) della transizione elettronica relativa.
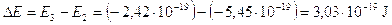
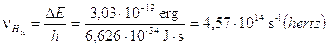
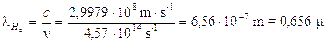
Il modello di Bohr è in grado di giustificare in modo soddisfacente solo il comportamento spettrale dell’Idrogeno e degli atomi idrogenoidi (ioni di altri elementi leggeri con un solo elettrone, come He+ e Li2+), mentre risulta inadeguato per atomi plurielettronici. D'altra parte quando Bohr impose la sua condizione di quantizzazione non poté darne alcuna giustificazione teorica, se non quella che in tal modo era possibile calcolare il valore numerico della costante di Rydberg e le righe spettrali dell’Idrogeno. Solo una decina di anni più tardi Louis De Broglie, avrebbe dimostrato che la condizione imposta da Bohr era una conseguenza della natura ondulatoria dell'elettrone.
Conferme sperimentali del modello di Bohr
Tra il 1913 ed il 1914 venne un'ulteriore conferma del modello atomico di Bohr, grazie agli esperimenti condotti da Moseley sugli spettri di emissione a righe nella regione della radiazione X di vari elementi chimici.
Quando un elettrone del primo livello energetico (livello K) viene espulso, in seguito ad una collisione con un elettrone proiettile o in seguito ad irradiazione con fotoni altamente energetici (gli elettroni del primo livello sono fortemente legati), il suo posto può essere occupato da un elettrone presente nei livelli superiori. Se l'elettrone proviene dal livello L (n = 2) la riga spettrale che si forma è detta K, se proviene dal livello M (n = 3) è detta K, e così via.
Se l'elettrone inizialmente espulso interessa il livello L, le righe che si formano per transizione elettronica dagli strati superiori M, N... sono dette L, L...
La serie K è sostanzialmente analoga alla serie di Lyman per l'idrogeno, ma si manifesta nella regione X.
Le diverse righe della serie K presentano naturalmente un valore diverso nei vari elementi chimici, a causa delle differenze di energia esistenti tra livelli energetici dello stesso tipo in atomi aventi una diversa carica nucleare Z.
Moseley dimostrò che la riga più intensa di questi spettri (riga K) si spostava regolarmente quando si passava da un elemento al successivo nella tavola periodica e che la lunghezza d'onda di tale riga si poteva esprimere in funzione del numero atomico Z, attraverso una relazione sostanzialmente analoga alla relazione di Balmer
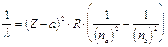
dove a è la costante di schermo, introdotta per tener conto del fatto che la carica del nucleo "vista" da ciascun elettrone è, a causa della presenza degli altri elettroni, inferiore a Ze.
Per la riga K la relazione diventa
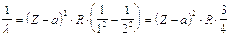
La relazione dimostra che la radice quadrata della lunghezza d'onda è inversamente proporzionale al numero atomico Z.
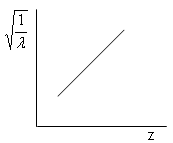
Spostamento delle righe K
in funzione del numero atomico Z
Ciò, oltre a confermare il modello di Bohr, permise, da una parte di dare al numero atomico Z il suo significato preciso di numero di cariche elettriche concentrate nel nucleo (e quindi anche di numero di elettroni orbitanti esternamente per rendere l'atomo neutro), dall'altra di ordinare correttamente gli elementi nella tavola periodica secondo il numero atomico crescente e non secondo il peso atomico crescente. Gli elementi devono infatti essere ordinati con lo stesso ordine con cui si succedono le righe della serie K. Risultò ad esempio che il Co precede il Ni e non viceversa .
Del 1914 sono gli esperimenti condotti da J. Franck e G. Hertz (nipote di H. Hertz) i quali scoprirono che gli elettroni, quando attraversano i vapori di Mercurio, subiscono una perdita di energia secondo “livelli” discreti e che a tale perdita di energia corrisponde una emissione di radiazioni ultraviolette (l = 254 nm) da parte del Mercurio. Pochi mesi più tardi Niels Bohr si rese conto che si trattava di una chiara conferma della validità del suo modello atomico quantizzato.
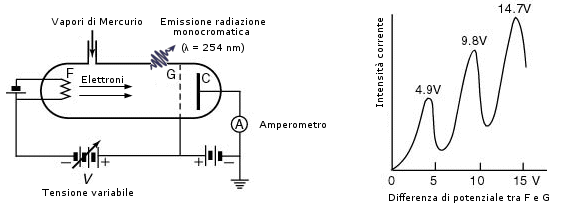
Esperimento di Franck-Hertz
Tra il filamento emittente F e la griglia G viene applicata una differenza di potenziale variabile. Tra la griglia G ed il collettore C viene applicata una differenza di potenziale costante di segno opposto di -1,5 V che esercita un’azione frenante, in modo che solo gli elettroni che hanno acquistato una sufficiente energia cinetica sono in grado di raggiungere il collettore C e contribuire alla circolazione di corrente. Finchè la differenza di potenziale è inferiore a 4,9 V gli elettroni urtano gli atomi di Mercurio in modo elastico, senza cedere energia e, attraversata la griglia, possiedono sufficiente energia per raggiungere il collettore e generare una corrente elettrica. la cui intensità viene misurata (amperometro). In corrispondenza di una tensione di 4,9 V gli elettroni hanno sufficiente energia per eccitare gli atomi di Mercurio che emettono una riga spettrale nell’ultravioletto a 254 nm. La cessione di energia agli atomi di Mercurio, rallenta gli elettroni, facendo diminuire l’intensità di corrente al collettore. Aumentando ulteriormente la tensione il fenomeno si ripresenta con regolarità per valori di tensione multipli di 4,9 V. Infatti, in corrispondenza di una tensione doppia (9,8 V) un elettrone ha sufficiente energia per eccitare in successione due atomi di mercurio, mentre con una tensione tripla (14,7 V) può eccitarne tre e così via.
Nel 1921 Otto Stern e W. Gerlach verificarono un'altra conseguenza della teoria di Bohr. Infatti non solo le singole orbite, ma anche l'intero atomo deve possedere un momento angolare quantizzato, calcolato come vettore risultante dei singoli momenti interni.
In pratica quindi anche l'intero atomo (se possiede un momento magnetico risultante netto) può assumere solo orientazioni spaziali discrete.
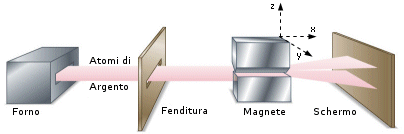
Esperimento di Stern-Gerlach
Un fascio di atomi di Argento attraversa un campo magnetico fortemente disomogeneo. I poli del magnete sono stati sagomati in modo che sul fascio di atomi agisca una forza deviante costante solo in direzione z e nulla in x ed y. Gli atomi si dividono in due fasci, colpendo lo schermo in due punti disposti simmetricamente rispetto alla direzione originaria. Gli atomi dimostrano pertanto di possedere un momento magnetico netto che si orienta in due soli modi possibili e controversi (spin antiparalleli) rispetto al campo magnetico applicato.
Il modello di Bohr-Sommerfeld : numero quantico secondario l
Tra le ipotesi iniziali di Bohr vi era quella che le orbite degli elettroni fossero circolari. Si trattava di un'ipotesi semplificatrice visto che la teoria di Bohr si basa sulla legge di Coulomb, formalmente simile alla legge di gravitazione universale, la quale costringe i corpi a ruotare intorno ad un baricentro comune su orbite ellittiche (la circonferenza può essere considerata un caso particolare di ellisse, con e = 0).
Nel 1915 A. Sommerfeld portò delle modificazioni al modello iniziale di Bohr, introducendo appunto delle orbite ellittiche in cui il nucleo occupava uno dei due fuochi, in modo del tutto analogo a quanto accade per le orbite planetarie.
Egli dimostrò che mentre nel primo livello l'elettrone poteva percorrere solo un'orbita circolare. nel secondo livello oltre ad un'orbita circolare l'elettrone avrebbe potuto occupare con la stessa energia, anche un'orbita ellittica avente l'asse maggiore della stessa lunghezza del diametro dell'orbita circolare.
Nel terzo livello era poi possibile per l'elettrone occupare, oltre all'orbita circolare due orbite ellittiche aventi assi maggiori uguali al diametro dell'orbita circolare, ma diversa eccentricità e cosi via.
L'introduzione delle orbite ellittiche sembrò rappresentare inizialmente una inutile complicazione nei calcoli. Esse permisero invece di risolvere il problema della cosiddetta struttura fine delle righe spettrali.
Con l'affinamento delle tecniche spettroscopiche risultò infatti che, utilizzando maggiori risoluzioni, ciascuna riga spettrale appariva composta da una serie di sottili righe molto ravvicinate, ad indicare la probabile esistenza di sottolivelli all'interno di ciascun livello energetico principale.
La teoria di Bohr era una teoria non relativistica, nel senso che non utilizzava nel suo formalismo le relazioni della relatività speciale. In effetti le equazioni della relatività speciale possono essere trascurate senza incorrere in errori eccessivi se i corpi che si stanno studiando presentano velocità molto inferiori alla velocità della luce. Nel caso la velocità del corpo oggetto di studio si avvicini a quella della luce, la relatività dimostra che la massa del corpo non rimane costante ma cresce al crescere della velocità in modo sensibile.
Tenendo presente che gli elettroni viaggiano a velocità molto elevate intorno al nucleo atomico, Sommerfeld introdusse le condizioni relativistiche nel modello di Bohr.
In pratica, ricordando che nel moto lungo un'ellisse l'elettrone è costretto a viaggiare più velocemente quando si trova più vicino al nucleo e più lentamente quando si trova più distante, la massa elettronica subisce delle modificazioni, aumentando in prossimità del nucleo e diminuendo nel punto più distante. Ciò comporta una diversificazione, seppur minima, delle energie associate alle orbite ellittiche, le quali non coincidono più con le energie delle orbite circolari del livello di appartenenza.
L'introduzione delle condizioni relativistiche da parte di Sommerfeld permise di spiegare in parte la struttura fine dello spettro.
Le orbite ellittiche di Sommerfeld resero però necessaria l'introduzione di un altro numero quantico detto numero quantico secondario o azimutale indicato con l.
l è un numero intero positivo il cui valore dipende dal valore assunto da n
0 £ l £ n - 1
Quindi
se n = 1 l = 0 ® orbita di tipo s
( ciò significa che nel primo livello vi è una sola orbita circolare, indicata appunto con l = 0, o anche con la lettera 's').
se n = 2 l = 0 ® orbita di tipo s
l = 1 ® orbita di tipo p
(ciò significa che nel secondo livello oltre ad una orbita circolare (l = 0), naturalmente di diametro maggiore della precedente, vi è anche un'orbita ellittica ( l = 1) indicata anche con la lettera 'p'.
se n = 3 l = 0 ® orbita di tipo s
l = 1 ® orbita di tipo p
l = 2 ® orbita di tipo d
(ciò significa che nel terzo livello possono trovar posto oltre ad un'orbita circolare s ed una ellittica di tipo p, una seconda orbita ellittica (l = 2), avente naturalmente eccentricità differente, indicata anche con la lettera 'd'.
se n = 4 l = 0 ® orbita di tipo s
l = 1 ® orbita di tipo p
l = 2 ® orbita di tipo d
l = 3 ® orbita di tipo f
(ciò significa che nel quarto livello, oltre alle precedenti orbite può trovar posto una terza orbita ellittica (l = 3), avente forma diversa ed indicata con la lettera 'f'.
In pratica il numero quantico secondario determina la forma dell'orbita descritta dall'elettrone. Comunemente però i quattro tipi di orbite possibili vengono per semplicità indicate con le lettere s, p, d ed f.
Le lettere s, p, d, f sono le iniziali dei termini con cui storicamente venivano indicate in spettroscopia le righe corrispondenti; sharp, principal, diffuse e fundamental.
Le orbite ellittiche presentano semiasse maggiore a = n2·ao e semiasse minore b = n·l·a0
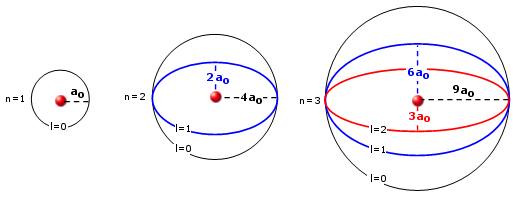
Orbite ellittiche di Sommerfeld per i primi tre livelli energetici (ao = raggio di Bohr)
Il numero quantico magnetico m
Il numero dei sottolivelli prodotto dall'introduzione delle orbite ellittiche non era comunque ancora sufficiente a giustificare tutta la ricchezza della struttura fine dello spettro.
Fin dal 1896 era noto che quando una sorgente luminosa viene sottoposta ad un campo magnetico, le righe spettrali vengono ulteriormente scomposte in diverse componenti (effetto Zeeman)
Il fenomeno può essere spiegato osservando che un'orbita elettronica si comporta come una spira percorsa da corrente elettrica e, come previsto da Ampere nel 1820, produce un momento magnetico che dipende dal suo momento angolare.
Poiché il momento angolare è quantizzato anche il momento magnetico lo è.
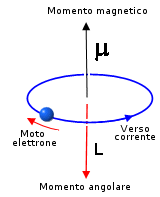
Si dimostra che il momento magnetico è sempre multiplo di una quantità minima detta magnetone di Bohr (mb)
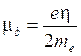
Ora è possibile dimostrare che una stessa orbita sottoposta ad un campo magnetico esterno può orientare il suo vettore momento magnetico solo in alcune direzioni, diversificando il suo contenuto energetico e dando perciò luogo ad ulteriori sottolivelli. Il numero delle direzioni consentite viene espresso dal cosiddetto numero quantico magnetico m che può assumere solo i valori interi compresi tra -l e + l.
-l £ m £ +l
In effetti tali sottolivelli vengono solamente resi più evidenti dall'effetto Zeeman. Essi esistono normalmente nell'atomo poiché le orbite elettroniche sono sottoposte al campo magnetico prodotto dal nucleo carico positivamente.
se l = 0 (orbita circolare s) m = 0
ciò significa che sottoposta ad un campo magnetico esterno un'orbita circolare dà luogo ad un’unica orientazione. Avremo perciò una sola orbita circolare di tipo s.
se l = 1 (orbita ellittica di tipo p) m può assumere i valori +1 0 -1
ciò significa che tale orbita può orientarsi in tre modi diversi producendo tre sottolivelli a differente energia. Avremo perciò 3 orbite di tipo p, indicate ciascuna con un diverso valore di m.
se l = 2 (orbita ellittica di tipo d) m può assumere i valori +2 +1 0 -1 -2
ciò significa che questo tipo di orbita ellittica può orientarsi in 5 modi differenti producendo quindi 5 sottolivelli a differente energia. Avremo perciò 5 orbite di tipo d, indicate ciascuna con un diverso valore di m.
se l = 3 (orbita ellittica di tipo f) m può assumere i valori +3 +2 +1 0 -1 -2 -3 ( ciò significa che questo tipo di orbita può orientarsi in 7 modi diversi, producendo 7 sottolivelli a differente energia. Avremo perciò 7 orbite di tipo f, indicate ciascuna con un diverso valore di m.
In pratica il valore del numero quantico magnetico determina il numero di orbite di una certa forma presenti in ciascun livello energetico principale.
Numero quantico di spin e principio di esclusione di Pauli
Il modello di Bohr-Sommerfeld rimane sostanzialmente invariato anche per atomi con maggior numero di protoni nel nucleo e quindi di elettroni in orbita intorno ad esso. L'unica differenza è in pratica dovuta al fatto che la maggior attrazione esercitata dal nucleo fa diminuire il diametro di tutte le orbite permesse. Il fatto permette di spiegare in modo naturale la diversità degli spettri dei vari elementi, in quanto essendo le orbite via via più compresse anche i salti quantici tra un'orbita e l'altra risultano di differente entità, producendo quindi righe spettrali peculiari.
Vi era tuttavia un problema in quanto per la fisica classica un sistema meccanico è stabile quando possiede il minor contenuto energetico. Pertanto tutti gli elettroni che vengono introdotti nelle orbite dopo il primo, dovrebbero naturalmente liberarsi della loro energia addizionale attraverso una serie di transizioni verso il primi livello energetico. Gli elettroni degli atomi pesanti dovrebbero perciò in definitiva trovarsi addensati tutti sulla prima orbita.
Poiché però tale orbita diventa sempre più piccola per l'attrazione esercitata dai nuclei via via più carichi positivamente, gli elementi più pesanti dovrebbero presentare atomi con diametro via via minore, mentre l'esperienza dimostra che ciò non è vero.
Nel 1925 il fisico tedesco Wolfgang Pauli formulò il principio noto come principio di esclusione, che permise di descrivere correttamente la distribuzione degli elettroni nelle diverse orbite.
Il principio di esclusione di Pauli afferma che ogni orbita quantica non può contenere più di due elettroni, i quali si differenziano per il valore di un quarto numero quantico detto numero quantico di spin. Il numero di spin può assumere solo i valori +1/2 e -1/2.
Con una formulazione alternativa, ma equivalente diremo
Il principio di esclusione di Pauli afferma che in un atomo non possono esistere 2 elettroni con tutti e quattro i numeri quantici uguali.
In altre parole ogni combinazione particolare dei quattro numeri quantici individua uno ed uno solo elettrone.
Ciò ha una conseguenza importante sulle configurazioni elettroniche, in quanto se entrambi i posti disponibili in un orbita sono occupati, gli elettroni successivi devono prendere posto necessariamente in orbite più esterne, sempre due per orbita.
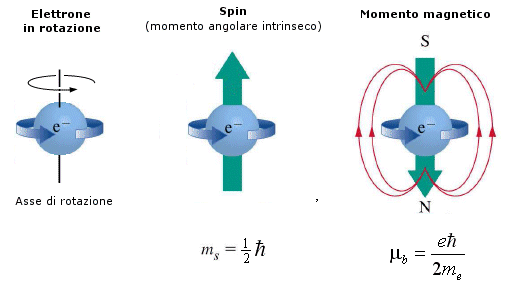
Nel novembre del 1925 G.E. Uhlenbeck e S.A. Goudsmit diedero significato fisico al numero quantico di spin, ipotizzando l'esistenza di un momento magnetico intrinseco dell'elettrone.
In altre parole è possibile immaginare l'elettrone carico negativamente come una piccola trottola che gira intorno al suo asse, in modo da produrre il momento magnetico osservato.
L’elettrone possiede un momento magnetico pari ad un magnetone di Bohr e, come conseguenza del suo moto di rotazione, anche un momento angolare intrinseco o spin, il cui valore può essere determinato in funzione del momento magnetico. Lo spin risulta essere pari a 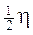 ed il suo verso è opposto al momento magnetico (a causa della carica negativa dell’elettrone)
ed il suo verso è opposto al momento magnetico (a causa della carica negativa dell’elettrone)
Il momento magnetico dell'elettrone, e quindi anche il suo momento angolare o spin, risulta quantizzato. Sottoposto ad un campo magnetico esterno lo spin dell’elettrone può infatti orientarsi nello stesso verso del campo o in verso opposto.
Convenzionalmente il vettore spin si considera parallelo alla direzione di avanzamento dell’elettrone, per cui i due elettroni si presenteranno:
- uno con spin
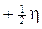
- l’altro con spin
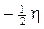

Dunque, in accordo con il principio di Pauli, in ogni orbita possono coesistere al massimo due elettroni i quali si distinguono per avere i vettori spin ad essi associati controversi o, come si usa impropriamente dire, antiparalleli.
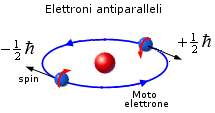
La scoperta dello spin dell'elettrone consentì di spiegare i risultati dell'esperimento di Stern-Gerlach. Gli atomi di argento possiedono infatti un numero dispari di elettroni ( Z = 47 ). Gli spin dei primi 46 elettroni si annullano a coppie, mentre lo spin dell'ultimo elettrone rimane come momento magnetico netto dell'intero atomo. In tal modo gli atomi che possiedono spin +1/2 vengono deflessi in una direzione, quelli che possiedono spin -1/2 in direzione opposta.
Nel 1926 Fermi fece una delle più feconde applicazioni del principio di esclusione, incorporandolo nella meccanica statistica ed ottenendo una nuova statistica, alternativa a quella già proposta da Bose e Einstein.
La formulazione del principio di esclusione e della statistica di Fermi che da esso deriva su basi rigorosamente quantistiche fu fatta da Dirac intorno al 1928. Tale statistica prende oggi il nome di statistica di Fermi-Dirac.
Solo nel 1940 Pauli scoprì un semplice criterio per determinare quali particelle obbediscono alla statistica di Bose-Einstein e quali alla statistica di Fermi-Dirac.
- Le particelle con spin intero sono descritte dalla statistica di Bose-Einstein e sono per questo dette bosoni. Esse non obbediscono al principio di esclusione di Pauli e possono presentarsi pertanto in numero qualsiasi nello stesso stato quantico, addensandosi numerose in uno stesso livello energetico.
- Le particelle con spin semidispari (semintero) sono descritte dalla statistica di Fermi-Dirac e sono perciò dette fermioni. Esse obbediscono al principio di esclusione di Pauli e non possono pertanto occupare lo stesso stato quantico, in numero superiore a due.
Il principio spiega in modo semplice anche la periodicità degli elementi chimici. Quando infatti un livello energetico risulta pieno di elettroni, i successivi sono costretti a riempire il livello energetico successivo, dove si trovano orbite dello stesso tipo del precedente, anche se di dimensioni maggiori. Gli elettroni si distribuiscono nei vari livelli con andamento regolare e periodico.
Poiché poi sono gli elettroni più esterni a fornire le caratteristiche chimiche all'elemento diventa ovvia anche la periodicità di tali caratteristiche che si riscontra nella tavola periodica.
Nella tavola periodica esistono quattro coppie di elementi (Ar/K, Co/Ni, Te/I, Th/Pa (Torio/Proattinio)) il cui ordine risulterebbe invertito se fossero ordinati secondo il peso atomico crescente. È notevole il fatto che Mendeleev decise di scambiarli di posto, pensando che il loro peso atomico fosse errato, classificandoli non in base al peso, ma alle loro caratteristiche chimiche
Spesso il magnetone di Bohr viene misurato utilizzando il sistema cgs elettromagnetico. In tal caso, per convertire la carica dell'elettrone, espressa in unità elettrostatiche (1 ues = statC = 1franklin), nelle corrispondenti unità elettromagnetiche (abCoulomb), è necessario dividerla per c, velocità della luce (1 abC = 10 C = c statC, con c = 3 1010 cm/s)) . La relazione diventa . Il magnetone di Bohr vale nel sistema SI 9,2740155.10-24 J T-1, nel sistema cgsem 9,2740155.10-21 erg G-1 e nel sistema cgses 2,7802799.10-10 erg statT-1.
Modelli atomici quanto-meccanici
Nonostante i notevoli successi nello spiegare lo spettro a righe, perfino a livello della sua struttura fine, anche il modello di Bohr-Sommerfeld, dimostrò la sua limitatezza. Soprattutto l'impostazione per così dire semiclassica che lo caratterizzava lasciava insoddisfatti molti fisici. In altri termini tale modello ricorreva ampiamente alle leggi classiche della meccanica e dell'elettromagnetismo, salvo poi essere costretto a fare vistose eccezioni, vietandone arbitrariamente l'applicazione in alcuni passaggi chiave. (orbite stazionarie dove l’elettrone non irraggia). La stessa condizione di quantizzazione risultava introdotta del tutto arbitrariamente.
Inoltre il modello otteneva risultati buoni ed aderenti ai dati sperimentali solamente per lo spettro dell'idrogeno, mentre non riusciva a fare previsioni soddisfacenti per gli atomi plurielettronici.
Il modello subì una radicale ed a tutt'oggi definitiva revisione con la nascita di una nuova meccanica, la meccanica quantistica e la conseguente introduzione di modelli atomici quantomeccanici.
La data di nascita della meccanica quantistica si può fissare al 1900 con la scoperta da parte di Planck del quanto di energia radiante h. Ma per circa vent'anni i fisici non ebbero vera consapevolezza della portata di tale scoperta. Le cose cominciarono realmente a mutare quando nel 1924 il fisico francese Louis De Broglie, avanzò la sconvolgente ipotesi che non solo l'energia, ma anche la materia possedesse una natura duale, corpuscolare e ondulatoria.
La natura ondulatoria della materia: De Broglie
Secondo tale ipotesi ad ogni corpo è possibile associare un'onda, che De Broglie chiamava 'onda di materia'. Per verificare questo assunto era necessario calcolare la lunghezza d'onda associata, ad esempio ad un elettrone, e poi controllare sperimentalmente se l'elettrone poteva produrre fenomeni tipicamente ondulatori come l'interferenza o la diffrazione, di entità compatibile con la lunghezza d'onda calcolata.
Il calcolo della lunghezza d'onda associata ad un corpo di massa m, fu eseguito da De Broglie.
Egli propose di assimilare completamente la trattazione delle particelle materiali a quella dei fotoni. Abbiamo già visto come nell'effetto Compton i fotoni possano essere considerati particelle con quantità di moto pari a
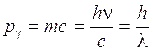
La relazione che nella relatività speciale lega l'energia totale (E), l'energia a riposo (Eo) e la quantità di moto p = mv è infatti E2 = (pc)2 + Eo2. Poiché non possono esistere fotoni fermi, l'energia a riposo di un fotone vale zero e la relazione per un fotone diventa E = pc.
Ricordando poi che E = h, si ottiene per un fotone 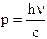 .
.
De Broglie ipotizzò dunque che anche la quantità di moto delle particelle materiali potesse essere calcolata come rapporto tra la costante di Planck e la loro lunghezza d'onda. Veniva in tal modo automaticamente associata ad ogni particella materiale una lunghezza d'onda, detta lunghezza d'onda di De Broglie, il cui valore è dato dalla relazione
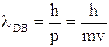
Sostituendo ad m la massa dell'elettrone e a v la velocità caratteristica dei raggi catodici, si può facilmente verificare che un elettrone possiede una lunghezza d'onda dello stesso ordine di grandezza dei raggi X (10-8 cm).
Utilizzando come reticolo di diffrazione reticoli cristallini come era stato fatto per dimostrare la natura ondulatoria dei raggi X, sarebbe stato dunque possibile verificare l'ipotesi di De Broglie con gli elettroni.
L'esperimento fu tentato nel 1927 da, George Thomson (figlio di J.J. Thomson) e, contemporaneamente da C.J. Davisson e L.H. Germer negli U.S.A. Essi dimostrarono che un fascio di elettroni accelerati e fatti passare attraverso un reticolo cristallino produce su di uno schermo caratteristiche figure di diffrazione e interferenza.
Dall'analisi del diametro degli anelli di diffrazione si poté anche calcolare che la lunghezza d'onda della radiazione elettronica coincideva perfettamente con quella prevista da De Broglie.
Si osservò anche che la lunghezza d'onda diminuiva o aumentava quando il fascio di elettroni veniva accelerato o rallentato, secondo quanto previsto dalla relazione di De Broglie.
Pochi anni dopo il fisico Otto Stern ottenne gli stessi risultati usando atomi di sodio al posto di elettroni, dimostrando quindi che tutte le particelle possono essere associate ad onde di De Broglie.
Il motivo per il quale non riusciamo ad osservare il comportamento ondulatorio degli oggetti macroscopici che ci circondano è dovuto al fatto che il rapporto h/mv risulta per tali oggetti piccolissimo, essendo h molto piccolo ed m molto grande.
Ai corpi macroscopici è dunque associata una lunghezza d'onda di De Broglie di dimensioni infinitesime.
Dopo aver sperimentalmente verificato la consistenza dell’ipotesi di De Broglie sulla natura ondulatoria della materia, i fisici si interrogarono sulla natura fisica di un’onda associata alla materia.
In ogni fenomeno ondulatorio c'è sempre qualcosa che si muove o vibra. I fisici si chiesero che cosa vibrasse nei corpi materiali. Lo stesso De Broglie tentò di dare una risposta ipotizzando che si trattasse di vere e proprie onde di materia. In altre parola che la stabilità della materia fosse solo un'illusione del mondo macroscopico, ma che a livello microscopico fosse necessario immaginare elettroni, protoni e atomi come delle nuvolette di materia pulsante senza contorni ben definiti.
Tale interpretazione non ebbe successo, anche perché si scontrava con difficoltà teoriche insormontabili. La risposta, ancor oggi accettata dalla maggior parte dei fisici, venne pochi anni più tardi, da parte di Max Born, segnando il definitivo tramonto del determinismo in fisica.
Natura ondulatoria della materia: interpretazione probabilistica
La descrizione ondulatoria della materia richiede un cambio radicale di prospettiva nel modo di interpretare i fenomeni. Soprattutto quando si passa dal continuo al discreto e viceversa, si assiste spesso ad una perdita di significato di concetti ormai assimilati ed accettati. Un esempio servirà a chiarire ed a familiarizzare con il problema.
Nei fenomeni radioattivi la velocità di decadimento 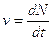 , cioè il numero di atomi che decadono per unità di tempo è direttamente proporzionale al numero iniziale N di atomi: v = lN.
, cioè il numero di atomi che decadono per unità di tempo è direttamente proporzionale al numero iniziale N di atomi: v = lN.
l è detta costante di decadimento radioattivo e rappresenta la frazione di atomi che decadono nell’unità di tempo. Poniamo ad esempio l = 0,01 s-1. Ciò significa che decadono l’1% di atomi al secondo. Se consideriamo un campione iniziale di 10.000 atomi, dopo 1 secondo ne sono decaduti 100; dopo 2 secondi altri 99 (l’1% dei rimanenti 10.000 – 100 = 9.900) e così via.
Consideriamo ora un campione costituito da un singolo atomo, N = 1 e chiediamoci che significato possiamo ora dare a l. Non possiamo certo affermare che in un secondo decadrà 1/100 di 1 atomo. Un atomo, o decade, o non decade. In tal caso l rappresenta dunque la probabilità che un atomo decada nell’unità di tempo. Così l’atomo presenta 1 probabilità su 100 di decadere dopo un secondo, 2 probabilità su 100 di decadere dopo 2 secondi,…..100 su 100 di decadere dopo 100 secondi. Si comprende così il motivo per cui la vita media di un atomo radioattivo è pari al reciproco della sua costante di decadimento.
In modo simile, nell'interpretazione di Born, l'onda associata ad una particella materiale deve essere interpretata in termini di probabilità di trovare la particella in un certo volume di spazio. Su tale interpretazione torneremo più avanti, dopo aver parlato dei fondamentali apporti alla meccanica quantistica forniti da Schrödinger ed Heisenberg.
L’introduzione della interpretazione ondulatoria della materia permise a De Broglie di portare ulteriore chiarezza all'interno del modello di Bohr-Sommerfeld. Alcuni fatti che inizialmente potevano apparire arbitrari e gratuiti ora acquistavano significato.
In particolare De Broglie dimostrò che la condizione di quantizzazione del momento angolare, introdotta in modo alquanto artificioso da Bohr, poteva essere derivata direttamente dalla natura ondulatoria dell'elettrone e ne diventava una sua naturale conseguenza.
Partendo dunque dalla condizione quantistica di Bohr 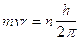 , sostituendo opportunamente nella prima si ottiene
, sostituendo opportunamente nella prima si ottiene
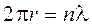
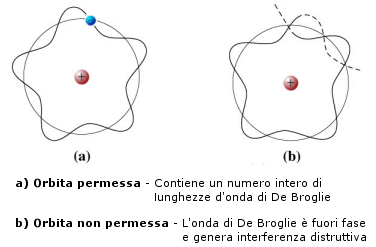
Ciò significa che le orbite quantizzate di Bohr devono soddisfare la condizione di contenere un numero intero n di lunghezze d'onda di De Broglie.
E precisamente, visto che n è il numero quantico principale, la prima orbita deve contenere una lunghezza d’onda, la seconda orbita due lunghezze d’onda e così via.
Si formano in tal modo delle onde, dette onde stazionarie, tali che dopo un'orbita completa l'onda si trova esattamente in fase con se stessa. Le altre orbite non sono consentite poiché in qualsiasi altro caso ventri e cavi delle onde si sovrapporrebbero creando interferenza distruttiva. L'onda si estinguerebbe e con essa la probabilità di trovare l'elettrone.
È la stessa condizione che fissa la frequenza di vibrazione di un oscillatore vincolato, ad esempio una corda vibrante di lunghezza fissata.
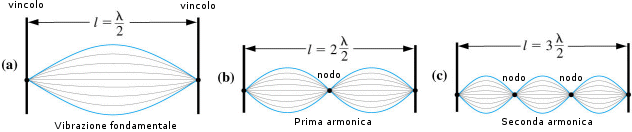
Ad esempio una corda di chitarra di lunghezza L è vincolata, è cioè fissa in due punti (il ponte ed il capotasto) che ne condizionano la vibrazione. Ciò e dovuto semplicemente al fatto che i due punti vincolati non sono naturalmente in gradi di vibrare.
Tenendo ora presente che lungo la corda in vibrazione si distinguono punti in cui l'oscillazione è massima (ventri e creste) e punti in cui è nulla (nodi). La distanza tra i nodi è ovviamente pari a l/2.
Ora, una corda vincolata non è in grado di produrre qualsiasi vibrazione, poiché due nodi sono fissi per definizione in quanto coincidono con i vincoli e gli altri nodi si possono disporre, equidistanti, in modo da dividere la corda in parti uguali.
Vengono in tal modo automaticamente a formarsi solo certe caratteristiche lunghezze d'onda.
In altre parole la corda può necessariamente contenere solo un numero intero di mezze lunghezze d’onda e quindi può produrre solo quelle vibrazioni per le quali vale la relazione
L = n (l/2) n = 1, 2, 3, 4........
dove L è la lunghezza della corda.

In un oscillatore vincolato si possono dunque formare solo onde stazionarie, aventi una determinata lunghezza d'onda.
Possiamo affermare che data una certa lunghezza della corda di un particolare strumento essa possiede un caratteristico spettro discontinuo (a righe).
Quando la corda contiene mezza lunghezza d'onda la frequenza corrispondente è detta fondamentale, mentre le frequenze superiori sono dette armoniche.
Il timbro del suono, che identifica uno strumento permettendo di distinguere due note uguali emesse da strumenti diversi, è determinato dalla sovrapposizione della vibrazione fondamentale con un certo numero di armoniche, tipiche di quel dato strumento. In altre parole il timbro è l'analogo in acustica dello spettro a righe di una sostanza in spettroscopia. La natura ondulatoria dell'elettrone, "vincolato" dal nucleo che lo attrae, rende l'atomo molto simile ad uno strumento musicale.
Il modello quantistico di Bohr-Sommerfeld acquista con De Broglie caratteristiche ondulatorie che ne giustificano i postulati di base.
La meccanica ondulatoria di Schrödinger
L'ipotesi di De Broglie fu generalizzata e formalizzata dal fisico austriaco E. Schrödinger, che nel 1926 ottenne un'equazione valida per il moto di una qualsiasi particella in un campo di forza, detta equazione d’onda Ψ (la lettera greca psi) o equazione di Schrödinger.
L’equazione d’onda, che descrive l’elettrone ha caratteristiche analoghe a quelle che descrivono le onde stazionarie nella meccanica classica. In entrambi i casi l’onda modifica la sua ampiezza passando alternativamente da valori positivi a negativi. I punti in cui il segno dell’onda cambia (da positivo a negativo o viceversa) e l’onda presenta ampiezza nulla si chiamano nodi.
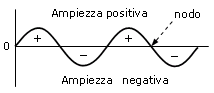
L'equazione d’onda di Schrödinger può essere applicata anche ad atomi diversi da quello dell’Idrogeno e risolta (anche se attraverso approssimazioni) con risultati in buon accordo con i dati sperimentali.
Quando si risolve l’equazione d’onda per un atomo particolare si ottiene una equazione parametrica, detta funzione d'onda , che presenta come parametri i primi tre numeri quantici, n, l, m.
Una funzione d’onda alla quale vengano attribuiti opportuni valori numerici ai numeri quantici individua lo stato di un particolare elettrone e prende il nome di funzione orbitalica o funzione orbitale..
Ogni funzione orbitale corrisponde ad uno stato stazionario dell’elettrone-onda.
Schrödinger arrivò alla conclusione che l'equazione d'onda che descrive un oscillatore meccanico poteva essere applicata anche all'atomo. Ora in acustica se la frequenza fondamentale è x la frequenza della seconda, terza, quarta......ennesima armonica sarà 2x, 3x, 4x......nx. In altre parole sarà sufficiente un solo parametro ( il numero intero positivo n = 1,2,3..) per individuare qualsiasi armonica.
Nel caso delle onde di Schrödinger il problema è più complesso poiché le onde in questione sono tridimensionali e sono necessari tre parametri per determinare una qualsiasi armonica. Tali parametri saranno anche in questo caso necessariamente quantizzati visto che l'onda in questione è un'onda vincolata e quindi stazionaria.
La natura ondulatoria dell'elettrone, "vincolato" dal nucleo che lo attrae, rende l'atomo molto simile ad uno strumento musicale.
Tuttavia la meccanica che descrive le proprietà ondulatorie delle particelle quali l’elettrone differisce in modo sostanziale dalla meccanica classica ed è nota come meccanica quantistica.
La meccanica quantistica ci permette di ottenere informazioni su di una particella risolvendo l’equazione d’onda. L’informazione che si ottiene non è la posizione e la velocità della particella, ma la probabilità di trovarla in una determinata regione di spazio.
Dati certi valori ai numeri quantici n. l ed m, le soluzioni dell'equazione di Schrödinger non forniscono le coordinate del punto P in cui si dovrebbe trovare l'elettrone rispetto al nucleo posto idealmente all'origine degli assi, ma il valore che in quel punto assume la funzione d'onda Y.
Ciò costringe ad abbandonare il concetto di traiettoria definita e quindi di orbita, per introdurre quello di orbitale, inteso come regione di spazio intorno al nucleo alla quale associare una certa probabilità di trovarvi l'elettrone.
Si può dunque descrivere il comportamento di un elettrone attorno ad un nucleo mediante la risoluzione dell’equazione di Schrödinger dove l’energia potenziale è quella esercitata da una carica positiva localizzata sull’origine (nucleo). Il sistema più semplice è l’atomo di idrogeno che contiene un solo elettrone ed è l’unico sistema per cui l’equazione di Schrödinger può essere risolta esattamente.
Come abbiamo già detto in precedenza, l’equazione d’onda che descrive il comportamento degli elettroni all’interno di un atomo presenta diverse soluzioni possibili, dette funzioni d’onda Ψ o funzioni orbitaliche o, semplicemente, orbitali. Gli orbitali s, p, d, f sono descritti da altrettante funzioni orbitaliche. Lo stato di un elettrone è descritto dalla funzione d’onda Ψ.
Tuttavia la funzione d’onda Ψ non ha significato fisico diretto. Si può invece dimostrare che la funzione Ψ2, nota come densità di probabilità fornisce la probabilità di trovare l’elettrone nell’unità di volume, in un determinata posizione dello spazio ad una data distanza dal nucleo ed è quindi proporzionale alla densità di carica presente.
Si noti l’analogia con la radiazione elettromagnetica, nel caso in cui si applichino grandezze caratteristiche del modello ondulatorio ad un singolo fotone. In un’onda elettromagnetica l’energia per unità di volume è proporzionale al quadrato dell’ampiezza dell’onda A2, dove l’ampiezza è data dall’intensità del campo elettrico o del campo magnetico ad esso concatenato. Se ora passiamo dal continuo al discreto e consideriamo la radiazione come un insieme di fotoni, A2 diventa una misura del numero di fotoni presenti nell’unità di volume e, per un singolo fotone, della probabilità di trovarlo nell’unità di volume.
Mentre Ψ può assumere anche valori negativi (l’ampiezza di un’onda può essere sia positiva che negativa), Ψ2 assume solo valori positivi (il quadrato di un valore negativo è sempre positivo ed una probabilità negativa non ha senso)
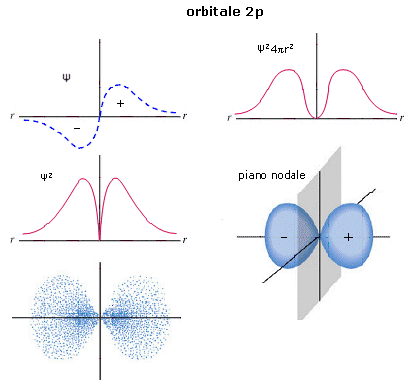
Le funzioni d’onda più semplici sono quelle che descrivono gli orbitali s.
Le funzioni d’onda Ψ(s) sono sfericamente simmetriche. La probabilità di trovare l’elettrone è la stessa in tutte le direzioni, variando solo con la distanza dal nucleo.
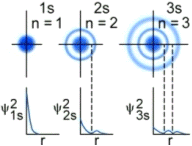
La rappresentazione di un’orbitale può essere fatta in modi diversi. Possiamo vederli esemplificati utilizzando una funzione orbitale particolarmente semplice, quella che descrive l’orbitale s del primo livello energetico (orbitale 1s) dell’atomo di Idrogeno.
1) Il modo più diretto di rappresentare un’orbitale è di tracciare la funzione orbitalica Y in dipendenza dal raggio. Per l’orbitale 1s dell’atomo di idrogeno essa vale
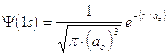
Si osserva facilmente che per r ® 0 il valore della funzione tende a 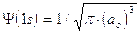 , mentre per r ® ¥ la funzione tende a zero. Il suo valore decresce dunque in modo esponenziale man mano che ci allontaniamo dal nucleo. L’orbitale 1s è infinitamente esteso (tutti gli orbitali lo sono).
, mentre per r ® ¥ la funzione tende a zero. Il suo valore decresce dunque in modo esponenziale man mano che ci allontaniamo dal nucleo. L’orbitale 1s è infinitamente esteso (tutti gli orbitali lo sono).
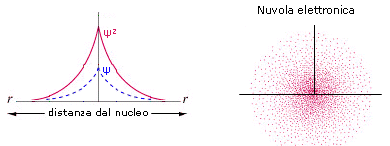
2) Poiché tuttavia la funzione orbitalica Y non presenta un significato fisico diretto si preferisce rappresentare l’orbitale riportando l’andamento della funzione densità di probabilità Y2. Si osserva facilmente che, per l’orbitale 1s, essa presenta lo stesso andamento della funzione orbitalica. La probabilità Y2 di trovare l’elettrone nell’unità di volume è massima e pari a 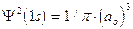 in corrispondenza del nucleo (r = 0), mentre diminuisce progressivamente allontanandoci da esso (r ® ¥).
in corrispondenza del nucleo (r = 0), mentre diminuisce progressivamente allontanandoci da esso (r ® ¥).
L’andamento di tale funzione viene spesso rappresentato in tre dimensioni attraverso la cosiddetta nuvola di carica o nuvola elettronica. Idealmente si può immaginare di osservare l’elettrone ad intervalli di tempo regolari e di riportare le sue posizioni come punti intorno al nucleo. Si ottiene una nebbia di punti che sfuma radialmente, detta appunto nuvola elettronica. Essa rappresenta una mappatura della funzione Y2. Nelle regioni dove la nuvola è più concentrata e la densità di punti è maggiore, risulta anche maggiore la probabilità di trovarvi l’elettrone.La probabilità Y2 di trovare l’elettrone nell’unità di volume è massima in corrispondenza del nucleo (r = 0), mentre diminuisce progressivamente allontanandoci da esso (r ® ¥). Ma in realtà il massimo di densità di probabilità non implica il massimo di probabilità.
3) Possiamo rendercene conto ricorrendo alla funzione di distribuzione radiale della probabilità, un modo alternativo di rappresentazione dell’orbitale che presenta il pregio di descriverlo in modo più intuitivo. Dividiamo lo spazio intorno al nucleo in gusci sferici concentrici di spessore infinitesimo dr. Il volume di un generico guscio di superficie 4pr2, che si trovi a distanza r, sarà pari a 4pr2dr e la probabilità di trovarvi l’elettrone si otterrà ovviamente come prodotto della probabilità di trovare l’elettrone nell’unità di volume Y2 ed il volume del guscio stesso.
dP = Ψ2 4πr2dr.
Il rapporto dP/dr rappresenta la variazione della probabilità al variare della distanza dal nucleo ed è quindi una funzione di distribuzione della probabilità in funzione del raggio (radiale)
dP/dr = Ψ2 4πr2
Tale funzione vale zero in corrispondenza del nucleo (r = 0) in quanto un punto possiede volume nullo, presenta un massimo in corrispondenza di ao (che per l’atomo di Idrogeno è pari 0.53Å e corrisponde al raggio della prima orbita di Bohr) e si annulla all’infinito.
Se sommiamo le probabilità di trovare l’elettrone in ciascun guscio fino ad una certa distanza r, otteniamo la probabilità totale di trovare l’elettrone nel volume compreso tra 0 ed r. (ciò equivale a calcolare l’integrale della funzione da 0 ad r). Tale probabilità complessiva è pari all’area sottesa dalla curva di distribuzione della probabilità. Poiché la funzione si annulla all’infinito, per ottenere una probabilità del 100% è necessario considerare un volume infinitamente grande intorno al nucleo.
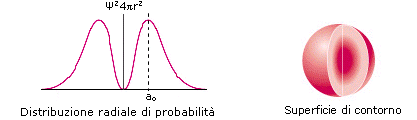
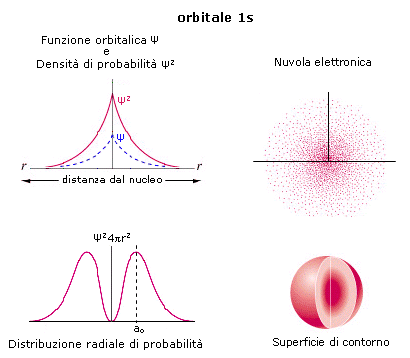
4) Se tuttavia ci accontentiamo di una probabilità inferiore, ad esempio del 95% o del 98%, possiamo individuare una superficie tale che la probabilità di trovarvi l’elettrone all’interno sia quella desiderata ed assumere il volume così individuato come rappresentativo dell’orbitale in questione. Tale superficie, detta superficie di contorno (boundary surface) o superficie di inviluppo o superficie limite, è sferica per gli orbitali s.
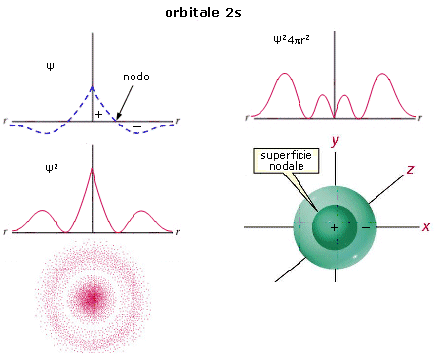
Anche l’orbitale 2s (orbitale s del secondo livello energetico) è sfericamente simmetrico, ma ad una certa distanza dal nucleo la funzione d’onda Ψ si annulla e da positiva diventa negativa (nodo). All’interno della superficie di controrno è pertanto presente una superficie nodale che separa la regione interna in cui la funzione d’onda è positiva dalla regione più esterna in cui la funzione d’onda è negativa. La superficie nodale, a probabilità nulla, separa due massimi, uno più vicino al nucleo ed un massimo principale più lontano.
Per l’orbitale 3s la funzione di distribuzione radiale di probabilità presenta tre massimi (due secondari e un massimo principale) e due punti nodali. La superficie di inviluppo contiene quindi due superfici nodali.
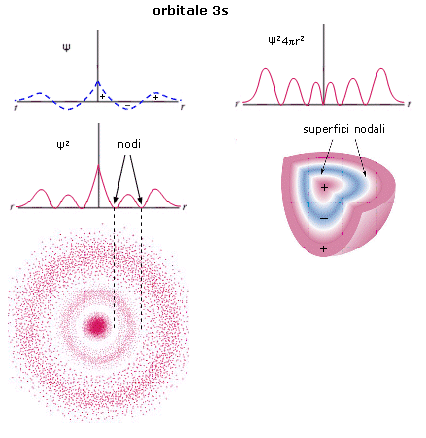
Gli orbitali ns dei livelli superiori mantengono la simmetria sferica e presentano n massimi di densità elettronica ed n-1 superfici nodali (con n = livello energetico di appartenenza).
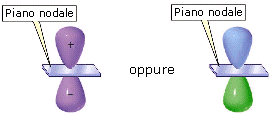
Gli orbitali p hanno simmetria cilindrica, possiedono cioè un asse preferenziale e non cambiano segno per rotazione attorno ad esso. Sono costituiti da due lobi ad elevata densità elettronica (in cui la funzione d’onda Ψ assume segno opposto) ed un piano nodale nell’origine (nucleo). Spesso le superfici di contorno vengono rappresentate con un colore diverso per i due lobi ad indicare il diverso segno (positivo e negativo) della funzione d’onda.
Gli orbitali p sono tre per livello energetico (tranne il primo livello energetico) ed essendo orientati uno perpendicolarmente all’altro nella direzione dei tre assi cartesiani, vengono indicati con la notazione: px, py, pz.
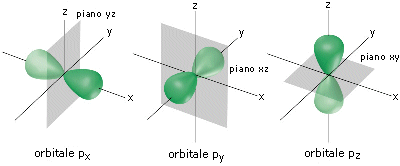
Gli orbitali 2p presentano un piano nodale passante per il nucleo che separa due lobi in cui la funzione d’onda Ψ presenta segni opposti senza alcuna altra superficie nodale al loro interno.
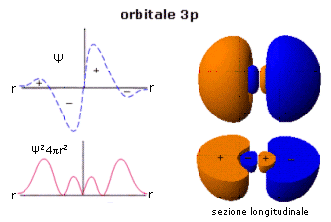
Gli orbitali 3p presentano un piano nodale passante per il nucleo che separa due lobi ad elevata densità elettronica. Ciascun lobo è diviso da una superficie nodale in due regioni in cui la funzione d’onda Ψ presenta segni opposti. La superficie nodale, a probabilità nulla, suddivide ciascun lobo in due massimi di probabilità, uno secondario più vicino al nucleo ed uno principale più lontano.
Gli orbitali 4p presentano ciascun lobo suddiviso in 3 regioni (in cui la funzione d’onda Ψ presenta segni alternativamente opposti) da due superfici nodali.

Gli orbitali np dei livelli superiori mantengono la simmetria cilindrica e presentano ciascun lobo suddiviso in n-1 regioni a massima densità elettronica separate da n-2 superfici nodali (con n = livello energetico di appartenenza).
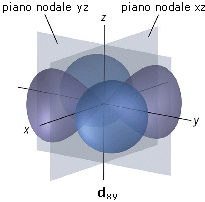
Gli orbitali d sono 5 per livello energetico (tranne i primi due livelli energetici). Quattro di essi sono tetralobati con i 4 lobi in cui la funzione d’onda Ψ assume segno alternativamente opposto. Il quinto orbitale d è bilobato con una regione anulare (in cui la funzione d’onda ssume segno opposto) ad alta densità elettronica che circonda il nucleo.

Gli orbitali d tetralobali presentano due piani nodali. Ad esempio l’orbitale dxy presenta due piani nodali perpendicolari che si intersecano sull’asse z
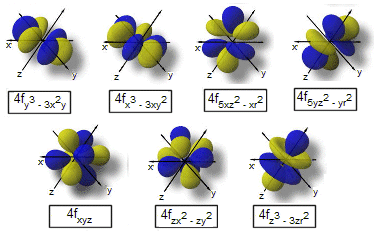
Gli orbitali f sono 7 per livello energetico (tranne i primi tre livelli energetici).
Il significato generale dei numeri quantici n, l ed m rimane inalterato anche se è necessario fare le seguenti precisazioni:
- Il valore assunto da 'n' determina l'energia dell'orbitale ed individua i 7 livelli energetici possibili, detti anche strati o gusci.
- il valore assunto da 'l' è associabile al tipo ed alla forma dell'orbitale. Esistono 4 tipi di orbitali. Gli orbitali 's' presentano simmetria sferica, gli orbitali 'p' presentano una forma a otto di rotazione, gli orbitali 'd' ed 'f' forme complesse.
- il valore assunto da 'm' è associabile al numero di orbitali per tipo presenti in ciascun livello energetico.
- Naturalmente anche il modello di Schrödinger prevede l'esistenza del quarto numero quantico di spin e non possono essere presenti più di due elettroni per orbitale
1° Livello energetico
1 orbitale s (1s) capienza max: 2 elettroni
2° Livello energetico
1 orbitale s (2s) capienza max: 2 elettroni
3 orbitali p (2p) capienza max: 6 elettroni
3° Livello energetico
1 orbitale s (3s) capienza max: 2 elettroni
3 orbitali p (3p) capienza max: 6 elettroni
5 orbitali d (3d) capienza max: 10 elettroni
4° Livello energetico
1 orbitale s (4s) capienza max: 2 elettroni
3 orbitali p (4p) capienza max: 6 elettroni
5 orbitali d (4d) capienza max: 10 elettroni
7 orbitali f (4f) capienza max: 14 elettroni
I livelli successivi presentano al massimo la struttura orbitalica del quarto livello. Gli atomi più pesanti, come l’Uranio, hanno elettroni a sufficienza per occupare 7 livelli energetici, senza tuttavia riuscire a riempirli completamente.
Anche se, in teoria, i livelli energetici più esterni possono presentare tutti i tipi di orbitali, in pratica un atomo non possiede mai un numero di elettroni sufficiente a riempire tutti i possibili orbitali esterni. Così la struttura orbitalica di un atomo è, in pratica, la seguente
Livello |
Orbitali consentiti |
Campienza elettronica |
|||
1° |
1s |
|
|
|
2 |
2° |
2s |
2p |
|
|
2+6=8 |
3° |
3s |
3p |
3d |
|
2+6+10=18 |
4° |
4s |
4p |
4d |
4f |
2+6+10+14=32 |
5° |
5s |
5p |
5d |
5f |
“ |
6° |
6s |
6p |
6d |
|
“ |
7° |
7s |
|
|
|
" |
I tre orbitali p di un medesimo livello energetico presentano lo stesso contenuto energetico e si dicono pertanto isoenergetici o degeneri. Questo accade anche per i cinque orbitali d di un medesimo livello energetico e per i sette orbitali f di un medesimo livello energetico.
La meccanica matriciale di Heisenberg
Nello stesso periodo in cui Schrödinger metteva a punto la sua equazione, apparve un lavoro teorico sulla teoria dei quanti di un giovane fisico tedesco, Werner Heisenberg.
Secondo Heisenberg le variabili meccaniche delle particelle. quali la posizione, la quantità di moto, la forza etc potevano essere rappresentate non da numeri ordinari, ma attraverso strutture matematiche complesse, dette matrici. L'algebra delle matrici è molto simile all'algebra ordinaria con la notevole eccezione che la moltiplicazione non gode della proprietà commutativa. Nell'algebra delle matrici il prodotto A x B non è necessariamente uguale al prodotto B x A.
Heisenberg dimostrò che se si rappresentano tutte le grandezze che compaiono nelle equazioni della meccanica classica come matrici e si introduce la condizione aggiuntiva che la differenza tra il prodotto della quantità di moto (p) per la posizione della particella (x) e il prodotto della posizione per la quantità di moto sia uguale ad 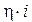 , con h costante di Planck ed i unità immaginaria, si ottiene una teoria che permette di descrivere tutti i fenomeni quantistici noti.
, con h costante di Planck ed i unità immaginaria, si ottiene una teoria che permette di descrivere tutti i fenomeni quantistici noti.
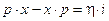
Se vivessimo in un mondo in cui h = 0, il prodotto px sarebbe uguale al prodotto xp, varrebbe la proprietà commutativa e tutte le relazioni quantistiche si ridurrebbero alla formulazione classica. La realtà del mondo delle particelle non sarebbe governata da fenomeni di tipo discreto, ma di tipo continuo.
Heisenberg pose inizialmente la sua meccanica matriciale in alternativa alla meccanica ondulatoria di Schrödinger. Ma quando Paul Maurice Adrien Dirac venne a conoscenza della meccanica delle matrici pubblicò un articolo nel quale dimostrò che la formulazione di Schrödinger e di Heisenberg erano equivalenti sul piano matematico. Le matrici di Heisenberg rappresentavano infatti le soluzioni tabulate dell'equazione di Schrödinger e nella soluzione di qualsiasi problema quantistico si può usare indifferentemente la meccanica ondulatoria o la meccanica delle matrici.
Il principio di indeterminazione di Heisenberg
Sebbene oggi venga prevalentemente utilizzato l'approccio ondulatorio di Schrödinger, la meccanica matriciale di Heisenberg ha prodotto un risultato teorico di enorme portata, che ci costringe a mettere in discussione dalle radici il nostro modo di concepire la realtà.
Posto che in meccanica quantistica si dicono coniugate coppie di grandezze il cui prodotto ha le dimensioni di un momento angolare, Heisenberg dimostrò che non è possibile misurare simultaneamente con una precisione grande a piacere due variabili coniugate.
Se consideriamo ad esempio le due variabili coniugate:
- posizione x di una particella rispetto all’origine di un sistema di riferimento nella direzione x
- quantità di moto p = mv della medesima particella
le indeterminazioni o incertezze nelle loro misure Dx e Dp devono soddisfare la relazione
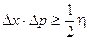
nota come principio di indeterminazione.
In pratica se misuriamo contemporaneamente la posizione e la quantità di moto di una particella, esisterà necessariamente una indeterminazione (incertezza) nella misura delle due variabili, tale che il loro prodotto è sempre maggiore o uguale ad un mezzo acca tagliato.
Una relazione analoga vale anche per altre coppie di variabili coniugate, come ad esempio per l'energia di una particella ed il tempo necessario per misurare tale energia.
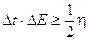
Si noti che Heisenberg ricavò tali relazioni direttamente dal formalismo matematico della teoria quantistica ed il principio risulta pertanto valido nella misura in cui vale la descrizione quantistica della realtà.
Il principio di indeterminazione non deriva dunque da una carenza nelle nostre tecniche di misurazione, ma è una conseguenza della teoria e, se questa è esatta, delle leggi di natura che la teoria descrive.
Il principio di indeterminazione condiziona evidentemente il livello di precisione delle nostre misurazioni e pone in definitiva dei limiti alla nostra capacità di conoscere la realtà. Infatti il miglior risultato che possiamo ottenere è quello in cui il prodotto delle indeterminazioni sia uguale ad un mezzo acca tagliato.
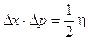
In questa caso le indeterminazioni sono inversamente proporzionali. Se dunque poniamo x ® 0, allora p ® ¥ il che significa che se tentiamo di rendere assolutamente precisa la misura della posizione di una particella (annullando l'incertezza insita nella sua determinazione), non possiamo più avere alcuna informazione riguardo alla sua quantità di moto, visto che l'indeterminazione ad essa associata diventa infinita e viceversa.
Si tratta di un'ulteriore conferma che in meccanica quantistica non è più possibile parlare di traiettorie determinate e quindi di orbite.
Certamente quando si ha a che fare con misurazioni di oggetti macroscopici è possibile trascurare il principio di indeterminazione senza incorrere in errori importanti.
Ad esempio per un corpo di massa 1 kg, tenendo conto che 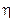 presenta un ordine di grandezza di 10-34 J s, possiamo in linea di principio determinare la sua posizione con un'indeterminazione di 10-15 m (con una precisione dell’ordine delle dimensioni di un nucleo atomico) e contemporaneamente la sua velocità con un'indeterminazione di 10-16 m/s, pari a 0,3 mm al secolo!
presenta un ordine di grandezza di 10-34 J s, possiamo in linea di principio determinare la sua posizione con un'indeterminazione di 10-15 m (con una precisione dell’ordine delle dimensioni di un nucleo atomico) e contemporaneamente la sua velocità con un'indeterminazione di 10-16 m/s, pari a 0,3 mm al secolo!
Ma nel caso di atomi e particelle subatomiche l’indeterminazione diviene ineludibile. Prendiamo ad esempio l’elettrone che viaggia intorno al suo nucleo. Esso possiede una velocità dell’ordine di un centesimo della velocità della luce.
La velocità dell’elettrone nell’atomo si può stimare eguagliando forza centrifuga e forza centripeta. Si ottiene
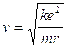
dove
m » 10-30 kg è la massa dell’elettrone,
e » 10-19 C è la carica dell’elettrone,
k » 10-9 è la costante di Coulomb
r » 10-10 m sono le dimensioni tipiche di un atomo.
Sostituendo opportunamente si ottengono valori dell’ordine di 106 m/s (circa un centesimo della velocità della luce).
Se ora ci proponiamo di misurare la velocità effettiva dell’elettrone con un’incertezza dell’1% pari a 104 m/s (1% di 106 m/s) dovremmo accontentarci di misurare la sua posizione con un errore di 10-8 m circa l’1% delle dimensioni atomiche.
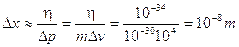
Possiamo dunque in un certo senso affermare che tanto più grande (massiccio) è un oggetto, tanto minori sono le sue caratteristiche ondulatorie (infatti l = h/mv) e tanto minore è la sua indeterminazione, cosicché gli oggetti macroscopici sono ‘in pratica’ perfettamente localizzabili.
I minuscoli elettroni presentano invece uno spiccato carattere ondulatorio ed una forte indeterminazione relativa, rendendo perciò necessario tutto lo spazio in più che noi osserviamo intorno al nucleo e che noi chiamiamo orbitale. Se cercassimo di confinare l’elettrone in una regione più piccola la sua lunghezza d'onda sarebbe costretta a diminuire ed è facile verificare che in tal caso l'elettrone vedrebbe aumentata la sua quantità di moto e quindi la sua energia cinetica.
Lo stesso ragionamento fu utilizzato per escludere la presenza di elettroni nel nucleo quando fu accertata l'emissione di radiazione beta da nuclei radioattivi. Infatti un elettrone confinato nella piccolissima regione nucleare (10-15 m) avrebbe un'energia troppo grande e verrebbe subito espulso. Gli elettroni che formano la radiazione beta devono quindi formarsi al momento del decadimento e non essere preesistenti ad esso.
L'equazione relativistica di Dirac
La meccanica ondulatoria di Schrödinger e tutti gli sviluppi fino al 1927 non sono relativistici. Tutti i tentativi fino ad allora compiuti per integrare la relatività ristretta alle equazioni quantistiche avevano portato a risultati assurdi o in netto contrasto con i dati sperimentali.
Nel 1928 finalmente Dirac trovò una equazione quantistico relativistica in grado di descrivere l'elettrone. Essa si riduce naturalmente per piccole velocità all'equazione di Schrödinger.
L'equazione di Dirac porta però un risultato notevole. Essa dà infatti automaticamente lo spin ed il momento magnetico dell'elettrone. Mentre queste proprietà in approssimazione non relativistica devono essere aggiunte e postulate separatamente, esse derivano direttamente dal formalismo matematico di Dirac.
L'equazione di Dirac descrive in realtà non solo il moto degli elettroni, ma anche di particelle di massa uguale, ma di carica positiva, del tutto sconosciute al tempo di Dirac. Ciò fu considerato da Dirac un grave difetto della teoria, tanto che egli tentò inutilmente di verificare se esse potevano essere identificate con i protoni.
In realtà Dirac aveva postulato l'esistenza dell'antiparticella dell'elettrone, il positrone, scoperto poi da C.D. Anderson nei raggi cosmici solo nel 1932.
Meccanica quantistica: interpretazioni
La nuova meccanica dei quanti pose notevoli problemi non solo nell’interpretazione fisica del formalismo matematico, ma accese un importante dibattito di natura filosofica ed epistemologica sulle sue implicazioni gnoseologiche.
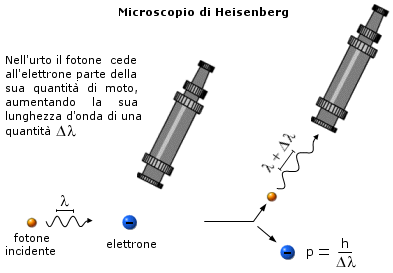
Il microscopio di Heisenberg
Heisenberg non si limitò a dar forma matematica al principio di indeterminazione, ma cercò in qualche modo di esplicitarne il significato che esso poteva assumere nell’ambito di una nuova teoria della conoscenza. Famoso rimane in questo senso l’esperimento mentale che egli propose nel 1927, noto come microscopio di Heisenberg.
Un esperimento mentale (o concettuale) è un esperimento “pensato” (Gedanke Experiment) e non realizzato, in cui lo sperimentatore può immaginare qualsiasi strumento o artificio, anche se non ancora tecnologicamente attuabile, purché il suo funzionamento sia compatibile e non contraddica le leggi della fisica.
Heisenberg immaginò dunque di voler osservare un elettrone inizialmente fermo, illuminandolo attraverso un fotone gamma avente lunghezza d'onda dello stesso ordine di grandezza rispetto alle dimensioni dell’elettrone (re » 10-15 m). Ricordiamo infatti che le onde possono essere usate per studiare oggetti che abbiano dimensioni maggiori o almeno dello stesso ordine di grandezza della lunghezza dell'onda usata .
Tuttavia, a causa della natura ondulatoria della luce, vi è una limitazione nel potere di risoluzione di uno strumento ottico. Due punti possono essere "risolti", cioè essere percepiti come separati, se la distanza che li divide è superiore alla lunghezza d'onda della radiazione usata per osservarli. Se illuminiamo un oggetto con luce visibile (l » 0,5m) non riusciremo a distinguere particolari di dimensioni inferiori a 0.5m .
Per questo motivo possiamo affermare che l'incertezza sulla posizione dell'elettrone sarà, in prima approssimazione, dell'ordine di grandezza della lunghezza d'onda della luce utilizzata
x
Appena viene colpito dal fotone, l'elettrone cambia velocità e direzione per effetto Compton, assorbendo una certa porzione dell'energia del fotone. Ricordando che la quantità di moto di un fotone è pari a
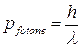
l'elettrone assumerà quindi dal fotone una quantità di moto incognita il cui valore può variare da 0 a 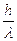 . La quantità di moto dell'elettrone presenterà quindi un'incertezza dello stesso ordine di grandezza della quantità di moto che il fotone potrebbe cedergli, pari a
. La quantità di moto dell'elettrone presenterà quindi un'incertezza dello stesso ordine di grandezza della quantità di moto che il fotone potrebbe cedergli, pari a
p 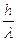
da cui, sostituendo la lunghezza d'onda dell'elettrone con x, otteniamo
x p h
La prima considerazione è che il principio di indeterminazione è una conseguenza della natura ondulatoria e quantizzata della materia. La distanza cruciale al di sotto della quale non ha più senso parlare di un'onda è la sua lunghezza d'onda. In altre parole noi definiamo come “onda” solo qualcosa che compie almeno una oscillazione completa, cioè che percorre almeno una lunghezza d'onda. Un'onda occupa quindi almeno una regione pari alla sua lunghezza.
In modo analogo la natura ondulatoria della materia introduce una indeterminazione in natura. La lunghezza d'onda della particella definisce una regione di incertezza, nel cui ambito la posizione della particella è sconosciuta ed inconoscibile.
La seconda considerazione è che, mentre nel mondo macroscopico noi possiamo interagire senza limitazioni con gli oggetti della nostra conoscenza, misurarli ed ottenere informazioni da essi senza modificarli in modo sostanziale, nel mondo subatomico non è per principio possibile trascurare le perturbazioni che le nostre misure arrecano alle stesse grandezze che misuriamo. Per poter misurare la posizione di un elettrone noi dobbiamo interagire con esso inviandogli almeno un fotone, ma questa interazione altera in modo imprevedibile lo stato di moto dell’elettrone.
Nel campo delle particelle atomiche e subatomiche è dunque necessario rinunciare alla pretesa di determinare in modo esatto tutte le variabili del moto. Alla classica visione deterministica del mondo è quindi necessario sostituire una visione probabilistica, in accordo con l'interpretazione di Born.
Si tratta però di una probabilità diversa rispetto a quella utilizzata dai fisici della seconda metà dell'Ottocento per costruire la meccanica statistica.
In quel caso le molecole di un gas venivano descritte su basi statistico-probabilistiche solo a causa dell'incompletezza dell'informazione sulle singole particelle.
Se noi infatti conoscessimo le condizioni iniziali di ogni singola particella del gas, possibilità questa che non viene per principio negata dalla meccanica statistica, saremmo in grado di determinare qualsiasi variabile con una precisione grande a piacere.
Il principio di indeterminazione distrugge dalle fondamenta questo modo di pensare. Noi non possiamo prevedere i movimenti delle singole particelle perché siamo nell'impossibilità teorica, e non solo pratica, di conoscere con esattezza le condizioni iniziali.
Inoltre la probabilità quantistica presenta caratteristiche peculiari rispetto alla probabilità ordinaria, delle quali parleremo in seguito,
Principio di complementarietà e interpretazione di Copenaghen
La scuola di Bohr a Copenaghen divenne negli anni tra il 1920 ed il 1930, il punto di riferimento per tutti coloro che si occupavano di meccanica quantistica. È qui che nasce una lettura critica ed una sintesi filosofica dei fenomeni connessi con il mondo dei quanti che va sotto il nome di interpretazione di Copenaghen.
I due cardini di tale interpretazione sono, da una parte l'interpretazione probabilistica di Born e di Heisenberg legate al significato della funzione Y2 e del principio di indeterminazione e dall'altra il cosiddetto principio di complementarietà introdotto da Bohr.
Nella sua interpretazione della meccanica quantistica Bohr pose l'accento sulla inadeguatezza del nostro linguaggio a descrivere i fenomeni quantistici.
Inoltre, afferma Bohr, è sbagliato pensare che il compito della fisica sia quello di scoprire come la natura è. La fisica verte su ciò che della natura si può dire.
Inoltre nella meccanica quantistica non è più possibile ignorare deliberatamente le interazioni tra apparato di misura e oggetto dell'indagine. Infatti l'atto stesso di osservare un oggetto quantistico ne modifica in linea teorica lo stato.
Nell'interpretazione di Bohr i concetti di particella e di onda cessano di essere incompatibili proprio per il fatto che il comportamento ondulatorio o corpuscolare dell'oggetto studiato dipendono dal tipo di esperimento e dal dispositivo sperimentale messo in atto per le misurazioni.
Bohr tiene ad esempio a sottolineare il fatto che gli stessi strumenti, costruiti per misurare variabili diverse, come ad esempio la posizione e la quantità di moto, sono essi stessi diversi ed incompatibili. Per misurare distanze occorrono infatti regoli rigidi ed indeformabili. Per misurare quantità di moto sono invece necessari strumenti con parti mobili in grado di deformarsi all'impatto, di fatto incompatibili con i primi.
Particelle ed onde sono dunque per Bohr complementari e devono ritenersi due manifestazioni di una stessa realtà che noi catturiamo in modo diverso per il fatto che essa viene modificata dal tipo di osservazione.
In sintesi l'interpretazione di Copenaghen della teoria quantistica da una parte rifiuta il determinismo sostituendo ad esso il carattere statistico-probabilistico della realtà, dall'altra produce una revisione radicale del concetto di oggettività, accettando che la realtà possa dipendere parzialmente dal modo in cui scegliamo di osservarla.
In altre parole, mentre nella fisica classica la realtà oggettiva esiste indipendentemente dall'osservatore, nella fisica quantistica, il modo in cui decidiamo di misurare l'oggetto condiziona l'immagine stessa che di questo oggetto ci possiamo rappresentare: la realtà oggettiva non ha più esistenza autonoma a prescindere dall'osservatore.
Nella primissima versione dell’Interpretazione di Copenaghen l’azione, attraverso la quale l’oggetto quantistico acquistava significato reale, doveva essere individuata nel pensiero dell'osservatore cosciente.
Successivamente si è arrivati a formulare una versione dell’Interpretazione di Copenaghen più debole e meno impegnativa dal punto di vista filosofico, dove viene eliminata la figura un po’ ingombrante da un punto di vista scientifico dell’ osservatore cosciente, sostituita da un “interpretazione operativa”. Secondo tale interpretazione, per poter misurare una caratteristica di un oggetto fisico, occorre necessariamente interagire con esso. Questa interazione è inevitabilmente “invasiva” e perturba lo stato originario, creando appunto la piccola "indeterminazione" e “costringendo” l’oggetto a manifestarsi.
Fu anche proposta un'interpretazione termodinamica secondo la quale la realtà quantistica resta in uno stato indefinito e "non-oggettivo" fino a quando non avviene una "reazione termodinamica irreversibile". Un esempio di fenomeno irreversibile è quello che avviene su una pellicola quando viene scattata una fotografia: non è possibile far ritornare la pellicola allo stato iniziale.
Ebbene, quando una particella quantistica interagisce con un sensore lascia dei segni irreversibili e ciò è sufficiente a rivelarlo nel "mondo oggettivo" della fisica classica senza la necessità di un soggetto cosciente che testimoni tale evento.
La probabilità quantistica ed il microscopio di Feynman
Al di là della naturale difficoltà ad accettare un mondo così poco familiare ed intuitivo come quello dei quanti, il comportamento delle particelle quantistiche presenta ulteriori stranezze.
Una di queste deriva dal fatto che la probabilità quantistica presenta un comportamento diverso rispetto alla probabilità ordinaria.
Infatti mentre in fisica classica le distribuzioni di probabilità di eventi indipendenti sono additive, in meccanica quantistica questo non avviene.
Se ad esempio vogliamo calcolare la probabilità che lanciando due dadi esca il numero 3, dobbiamo sommare tra loro la probabilità dei due eventi indipendenti E1 (esce 2 sul primo dado, esce 1 sul secondo: P1 = 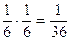 ).
).
Ptot = P1 + P2 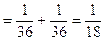
Se osserviamo ora due onde d'acqua sul mare che si accavallano possiamo notare che l'altezza complessiva dell'onda che si forma è data dalla somma delle altezze (ampiezze) delle singole onde. Se ad esempio in un certo punto dello spazio un'onda è al massimo ed una al minimo le due onde si annullano. Si tratta del principio di sovrapposizione che governa, come abbiamo già visto, tutti i fenomeni ondulatori, producendo i tipici processi di interferenza.
Anche le onde di probabilità della teoria quantistica, come le onde ordinarie, obbediscono al principio di sovrapposizione. Se cioè in una regione ci sono due onde di probabilità l'ampiezza totale risulta uguale alla somma delle ampiezze.
Ma la probabilità di trovare una particella in un certo punto non è data dall'altezza, che può essere anche negativa, ma dal quadrato della sua ampiezza (Y2).
Dunque, poiché le ampiezze si sommano in base al principio di sovrapposizione e poiché invece la probabilità è data dal quadrato dell'ampiezza, nella teoria dei quanti la probabilità totale non può essere calcolata sommando le probabilità parziali di eventi indipendenti.
Per esemplificare tale comportamento possiamo utilizzare un esperimento mentale proposto da Feynman nel 1960 e noto come microscopio di Feynman.
Immaginiamo di sparare dei proiettili verso uno schermo attraverso due finestre.
Inizialmente apriamo solo la prima finestra. Scopriamo che i proiettili si distribuiscono in modo caratteristico, che viene tipicamente descritto da una distribuzione di frequenza detta gaussiana (o “curva a campana” o anche “curva degli errori” perché descrive la distribuzione degli errori ed evidenzia come gli errori molto piccoli e molto grandi sono via via meno frequenti). Se i lanci effettuati sono sufficientemente numerosi la curva di frequenza diventa una buona misura della probabilità che possiede ciascun punto dello schermo di essere colpito.
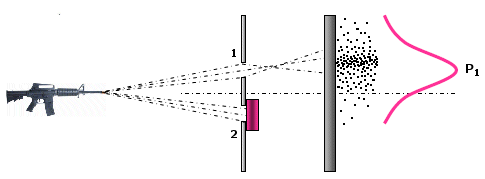
Se effettuiamo lo stesso esperimento tenendo chiusa la prima finestra e aprendo la seconda, potremo osservare un'analoga distribuzione nei colpi.
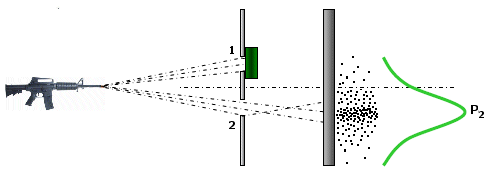
Aprendo infine entrambe le finestre scopriremo che nei punti in cui le due curve di probabilità si sovrappongono, i proiettili arrivano con maggior frequenza. Si può facilmente verificare che ora la probabilità che ciascun punto dello schermo venga colpito è esattamente la somma delle due curve di probabilità singole. Le probabilità non quantistiche di eventi indipendenti si sommano. Per i proiettili vale dunque Ptot = P1 + P2
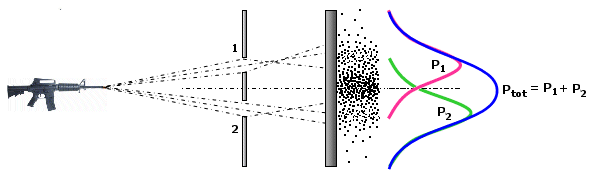
Eseguiamo ora l'esperimento facendo passare degli elettroni attraverso due fenditure sottili disposte parallelamente.
Quando è aperta solo la prima fessura gli elettroni producono sullo schermo una tipica figura di diffrazione che ritroviamo analoga nel caso venga aperta solo la seconda fenditura.
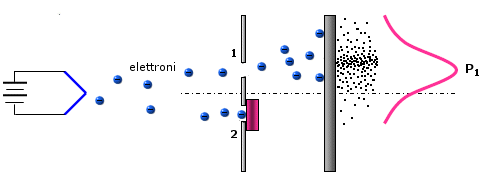
Gli elettroni colpiscono lo schermo più numerosi in una zona centrale per poi diradarsi alle estremità.
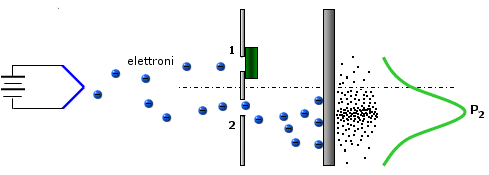
Ma nel caso le due fenditure vengano aperte contemporaneamente la curva di distribuzione totale degli elettroni non è data dalla somma delle due curve parziali. Sorprendentemente in alcuni punti in cui prima gli elettroni cadevano quando erano costretti a passare solo per una delle due fenditure, separatamente aperte, ora gli elettroni non cadono più. La curva che si ottiene è ancora una distribuzione di frequenza e quindi una misura della probabilità che gli elettroni hanno di colpire lo schermo, ma in tal caso essa non può essere ottenuta come semplice somma delle probabilità degli eventi separati ed indipendenti. Le probabilità quantistiche di eventi indipendenti non si sommano.
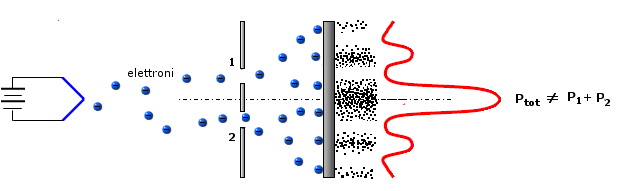
È necessario tener presente che gli elettroni arrivano sullo schermo rivelatore in modo discontinuo, venendo cioè captati attraverso singoli impulsi, come vere e proprie particelle. Nonostante ciò la loro distribuzione sullo schermo rivela il loro comportamento ondulatorio. In particolare la distribuzione di frequenza ottenuta con entrambe le fenditure aperte rivela chiaramente la presenza di fenomeni di interferenza, analoghi a quelli che si ottengono per la luce con un’esperienza di Young di doppia fenditura.
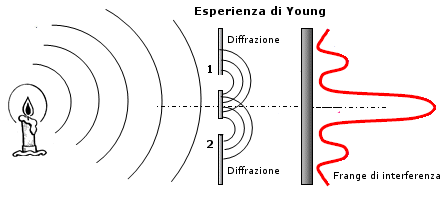
In effetti, secondo la teoria quantistica, non sono gli elettroni a comportarsi come onde, infatti colpiscono lo schermo come proiettili, ma è la probabilità di trovare l'elettrone che presenta un comportamento ondulatorio e viene diffratta dalle fenditure subendo quindi interferenza.
In tal caso la probabilità associata al passaggio dell'elettrone attraverso la fenditura 1 è pari a
P1 = (Y1)2
e la probabilità associata al passaggio dell'elettrone attraverso la fenditura 2 è pari a
P2 = (Y2)2
Quando entrambe le fenditure sono aperte le due onde Y1 e Y2 interferiscono, producendo una funzione d'onda che chiameremo Ytot
La probabilità totale sarà quindi pari al quadrato dell'onda prodotta dall'interferenza
Ptot = (Ytot)2
Si dimostra quindi facilmente che nel caso degli elettroni, dove il comportamento ondulatorio non può essere trascurato, la probabilità che essi colpiscano lo schermo con due fenditure aperte non può essere ottenuta come semplice somma delle probabilità che essi colpiscano lo schermo con le fenditure alternativamente aperte. Il quadrato di una somma è infatti diverso dalla somma dei quadrati
(Ytot)2 = (Y1 + Y2)2 ≠ Y12 + Y22
Tale risultato è tanto più sorprendente se si pensa che esso viene ottenuto anche facendo in modo che la sorgente di elettroni emetta un elettrone per volta.
Anche se si fanno passare, attraverso le due fenditure aperte, singoli elettroni a grandi intervalli di tempo l'uno dall'altro, essi andranno a cadere solo in corrispondenza dei massimi d'interferenza.
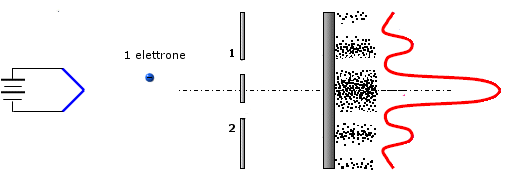
In altre parole il singolo elettrone "non sa" dove sono caduti gli elettroni precedenti e si avvia a colpire lo schermo sulla base della probabilità totale (Ytot)2. La situazione è analoga a quella del gioco dei dadi: se nei primi 5 tiri abbiamo ottenuto sempre il numero 3, la probabilità che al sesto tiro esca ancora 3 è sempre la stessa (1/18). Essa non varia come non varia la probabilità di tutte le altre combinazioni numeriche. Potremmo verificare che il 3 esce 1 volta su 18 tiri solo lanciando molte volte i dadi.
Il fatto che anche un singolo elettrone, il quale chiaramente interagisce con lo schermo come una particella (il cui urto è osservabile come un minuscolo lampo luminoso), si comporti in realtà durante il tragitto come un'onda, la quale, per poter interferire deve passare contemporaneamente attraverso entrambe le fenditure aperte, ci induce a chiederci se l'elettrone in quanto particella passi effettivamente o per la fenditura 1 o per la fenditura 2, quando entrambe le fenditure sono aperte.
È possibile tentare di rispondere a questa domanda cercando di osservare il passaggio dei singoli elettroni attraverso le fenditure. Collochiamo allora un rivelatore alle fenditure che ci informi del passaggio del singolo elettrone. Ad esempio potremo osservare l’elettrone, illuminandolo con un fotone (microscopio di Feynman). Saremo così in grado di sapere da quale fenditura è passato l'elettrone.
Ma nel momento in cui verifichiamo il passaggio dell'elettrone-particella attraverso una delle due fenditure, l'elettrone cessa di comportarsi come un'onda ed inizia a colpire anche le zone dello schermo che prima non colpiva: le frange di interferenza scompaiono.
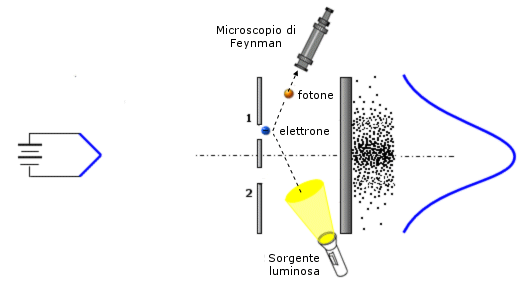
Quando dunque decidiamo di verificare se l'elettrone è una particella che passa realmente attraverso una delle due fenditure come un proiettile, esso si comporta effettivamente come una particella che attraversa la fenditura.
Prescindendo da un effettivo atto di osservazione non ha dunque senso parlare di esistenza oggettiva della particella in un dato punto dello spazio, ad esempio in corrispondenza di una delle due fenditure. È ciò che viene chiamata la realtà creata dall'osservatore.
Nel momento in cui lo osserviamo l'elettrone è una particella. Ma appena cessiamo di osservarlo si comporta come un'onda. Le diverse condizioni sperimentali alterano quindi in modo sensibile i risultati che noi possiamo ottenere.
Ecco quindi che, date le sostanziali differenze di preparazione degli esperimenti, la decisione tra un modello interpretativo e l'altro è compiuta all'atto stesso dell'osservazione. La “misurazione” diviene in un certo qual modo un nuovo ente che viene a far parte imprescindibilmente dello stesso fenomeno fisico sul quale si compie. Il particolare tipo di esperienza seleziona tra onda e corpuscolo.
La teoria quantistica afferma dunque l'impossibilità teorica di fare affermazioni relative alla natura oggettiva degli enti fisici studiati. Essa è una teoria che descrive il comportamento degli enti fisici date particolari condizioni sperimentali e non la loro essenza.
Anche se l'approccio quantistico può sembrare fortemente limitativo della nostra possibilità di conoscere il mondo, esso è in realtà comune a tutta la scienza.
Tutta la scienza si limita a descrivere il comportamento degli enti fisici e non formula affermazioni sulla loro essenza.
Quando ad esempio affermiamo che un filamento di oro è giallo, in realtà ciò non costituisce un'affermazione sull'essenza di questo elemento, ma descrive un suo comportamento in una particolare condizione sperimentale: quella di essere illuminato da luce bianca (o comunque radiazione contenente luce gialla). Se ad esempio esaminiamo il filamento con luce rossa esso appare nero, poiché assorbe tutta la radiazione che lo colpisce. Se poi il filamento viene reso incandescente esso appare rosso.
Se quello delle fenditure è un esperimento mentale, vi sono tuttavia numerosi dispositivi pratici di cui la tecnologia si serve comunemente e che sfruttano le singolari caratteristiche delle onde di probabilità.
Le onde che investono una nave ancorata lasciano un'ombra d'acqua calma grazie ad un fenomeno di diffrazione, studiando il quale è possibile risalire alla forma della nave. Ma se le stesse onde investono un palo affiorante il fenomeno è insensibile. Non incontreremo invece alcuna difficoltà ad analizzare la forma del palo studiandone l'ombra prodotta da onde luminose..
fonte: http://www.fileden.com/files/2008/11/5/2174401/Chimica.zip
fonte: http://rodomontano.altervista.org/chimica.php
sito web: http://rodomontano.altervista.org/
Autore del testo: Rodomontano
- Acidi
- Acidi e basi
- Acidi nucleici
- Acido folico e sulfamidici
- Acido salicilico
- Agenti chimici
- Aluminium Eng vers
- Analisi batteriologica acqua
- Appunti curiosi
- Biochimica
Biochimica industriale appunti
- Biochimica quiz
- Biocombustibili e biodiesel
- Chimica analitica glossario
- Chimica appunti
- Chimica appunti parte 1
- Chimica appunti parte 2
- Chimica appunti parte 3
- Chimica quiz
- Chimica e alchimia
- Chimica e gli alimenti
Chimica elementi gruppo 15
Chimica elementi gruppo 16
- Chimica farmaceutica
Chimica fotografia B&W
- Chimica generale
- Chimica generale 2
- Chimica generale 3
- Chimica generale 4
- Chimica generale 5
- Chimica generale 6
- Chimica generale 7
- Chimica generale 8
- Chimica generale 9
- Chimica generale 10
- Chimica generale appunti
- Chimica inorganica
- Chimica in versi
- Chimica in versi parte 2
Chimica peso molare
- Chimica misure e grandezze
- Chimica organica
- Chimica riassunto
- Chimica riassunti
- Chimica tabelle utili
- Chimica termini tecnici A
- Chimica termini tecnici B
- Chimica termini tecnici C
- Chimica termini tecnici D
- Chimica termini tecnici E
- Chimica termini tecnici F
- Chimica termini tecnici G H
- Chimica termini tecnici I
- Chimica termini tecnici L M
- Classific. e nomenclatura
- Cobalto e le sue leghe
- Coenzima q10 proprietà
- Composti organici biomole..
- Elementi chimici
- Elettrochimica
- Elettrolisi
- Esperimenti di chimica
- Esperimenti di chimica
- Glucidi riassunto
- Idrogeno caratteristiche
- Legami chimici
- Meccanica ondulatoria
- Microscopio di Heisenberg
- Modelli atomici
- Modelli atomici quanto-mec
- Monossido di carbonio
- Nomenclatura acidi ternari
- Nomenclatura idruri
- Numeri di ossidazione
- Osmosi inversa e idrologia
- Peso atomico azoto
- Peso atomico carbonio
- Peso atomico cloro
- Peso atomico ossigeno
- Peso atomico sodio
- Peso atomico zolfo
- Probabilità quantistica
- Quiz di chimica
- Riconoscimento gruppi
- Sali binari e sali ternari
- Storia della chimica
- Storia origini chimica
- Struttura atomica
- Struttura atomica 2
- Tabella punti di fusione
- Tavola periodica elementi
- Tavola periodica 2
- Valenza
Chimica appunti parte 2
Visita la nostra pagina principale
Chimica appunti parte 2
Termini d' uso e privacy
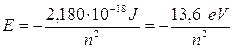
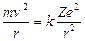
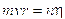
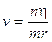 che sostituita nella 1) fornisce il raggio quantizzato
che sostituita nella 1) fornisce il raggio quantizzato 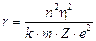
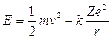
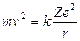 che sostituita nella 4) fornisce
che sostituita nella 4) fornisce 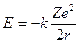
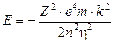
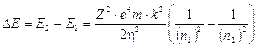
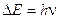 e dunque, dividendo entrambi i membri della 7) per ch, otteniamo
e dunque, dividendo entrambi i membri della 7) per ch, otteniamo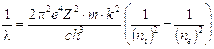
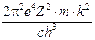 . È possibile tuttavia dimostrare che il moto combinato del sistema elettrone/protone attorno al baricentro comune è equivalente al moto di una particella di massa ridotta ()
. È possibile tuttavia dimostrare che il moto combinato del sistema elettrone/protone attorno al baricentro comune è equivalente al moto di una particella di massa ridotta ()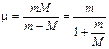
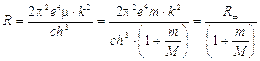
 è infatti il valore calcolato senza tener conto della massa del nucleo M, il che equivale ad ipotizzare un nucleo di massa M infinitamente grande per cui
è infatti il valore calcolato senza tener conto della massa del nucleo M, il che equivale ad ipotizzare un nucleo di massa M infinitamente grande per cui