Disegno tecnico geometria piana figure piane

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Disegno tecnico geometria piana figure piane

Costruzione del triangolo equilatero

Dato un riferimento assiale della figura, tracciare una circonferenza e scegliere un punto 1, che risulterà opposto al vertice A
Con la medesima apertura e puntando in 1, tracciare una porzione di circonferenza tale da intersecare la circonferenza inscrivente.
Unendo le due intersezioni C e B, ed il punto A, antipolare di 1, otterremo un triangolo equilatero.

NOTA: l'altezza del triangolo è 1,5 volte il raggio.

Costruzione di un quadrato

Dato un riferimento assiale della figura, tracciare una circonferenza.
Individuati i punti 1, 2, 3 di intersezione tra la circonferenza ed il riferimento assiale, col metodo delle bisettrici (puntando com medesima apertura in 1, 2, 3), si trovano i punti 4 e 5.
Tracciare dei segmenti che congiungano 4 e 5 col centro del sistema di riferimento, prolungandoli fino ad intersecare la circonferenza.
Da tali intersezioni vengono individuati i punti A, B, C, D per i quali tracciare il quadrato.

Costruzione del pentagono

Dato un riferimento assiale della figura, tracciare una circonferenza.
Individuare il punto medio M, pari alla metà del raggio.
Con apertura M-A e puntando in M, rintracciare sul medesimo asse il punto 1.
Con apertura A-1 tracciare una porzione di circonferenza fino ad individuare i punti E e B.
Con medesima apertura, puntando in E ed in B, si trovano C e D, ultimi punti del pentagono.

Costruzione dell'esagono

Dato un riferimento assiale della figura, tracciare una circonferenza e scegliere due poli A e D, tra loro opposti.
Con la medesima apertura e puntando sia in A che in D, tracciare due porzioni di circonferenza tali da intersecare la circonferenza inscrivente.
Unendo le intersezioni così ottenute con i poli scelti, si ottiene l'esagono.

NOTA: nell'esagono, il lato è pari al raggio.

Costruzione di un ellisse dati gli assi

Tracciare un sistema di riferimento assiale. Tracciare due circonferenze, la prima con apertura pari a metà asse minore (1-3), la seconda con apertura pari a metà dell'asse maggiore (2-4), prestabiliti dell'ellisse.
Dividere le circonferenze in più parti tracciando segmenti passanti per il centro, fino a trovare i punti ad esempio A e B sulle due circonferenze.
Tracciare un segmento orizzontale passante per A (o più genericamente per l'intersezione della circonferenza piccola).
Tracciare un segmento verticale passante per B (sulla circonferenza grande), in modo da farlo incontrare il segmento orizzontale tracciato in un punto C, facente parte della curva.
Più divisioni vengono fatte, più l'ellisse verrà preciso.

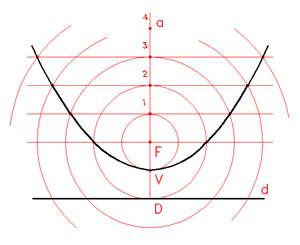Costruzione di una parabola dati fuoco e direttrice

Tracciare l'asse focale a, segnare la posizione del fuoco F e tracciare la direttrice d.
Il vertice V si trova esattamente alla metà della distanza tra il fuoco F e la direttrice d.
Tracciare quindi una circonferenza avente raggio F-V, fino a intersecare l'asse a in un punto che chiameremo 1.
Con medesima apertura, segnare sull'asse i punti 2, 3, 4 puntando in 1 per ottenere 2, in 2 per ottenere 3 e così via.
Tracciare una serie di circonferenze puntando sempre nel fuoco F, di raggio F-2, F-3, F-4, fin dove segnato. Tracciare una serie di rette parallele alla direttrice e tra loro, passanti per F, 1, 2, 3, 4. La prima circonferenza individua il vertice V.
La seconda circonferenza individua i primi punti della parabola nelle intersezioni con la retta passante per il fuoco F. La terza circonferenza, nell'intersezione con la retta passante per il punto 1. La quarta con la retta passante per 2, e così via.

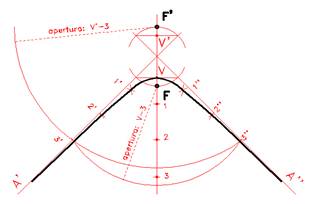Costruzione di un'iperbole dati gli asintoti ed i fuochi

Tracciare l'asse focale e i due asintoti, simmetrici rispetto ad esso ed incidenti in un punto C.
Tracciare una circonferenza puntando in C, con apertura CF=CF', ovvero rintracciando in modo simmetrico i due fuochi dati rispetto il punto C.
Congiungendo le intersezioni fra tale circonferenza e gli asintoti, otteniamo sull'asse focale la posizione dei vertici dell'iperbole.
Una prima considerazione è necessaria nell'evidenziare il rapporto geometrico tra vertici, fuochi, asintoti ed assi, così ottenuto.
Per ottenere gli altri punti della parabola, tracciare sull'asse focale una serie di punti 1, 2 3.. a distanze arbitrarie, opportune; per ottenere ad esempio i punti 3' e 3'', con apertura V-3, puntare in F tracciando una porzione di circonferenza; poi, con apertura V'-3, puntare in F' tracciando una seconda porzione di circonferenza. Le intersezioni determinano i punti dell'iperbole.

Costruzione di un ellisse dati gli assi

Tracciare gli assi dell'ellisse (1-3 e 2-4); completare un rettangolo inscrivente con misure dei lati pari a quelle degli assi. Sull'asse minore e su uno dei lati lunghi del rettangolo, tracciare una sequenza di punti, indicati in figura con a', b', c', ed a, b, c.
Il metodo pratico è individuare nei segmenti, la metà e la metà della metà, e segnare i punti.
Congiungere il punto 1 con a, b, c, a', b', c', prolungando questi tre fino al bordo del rettangolo.
Congiungere poi il punto 3 con c, b, a; le intersezioni di segmenti 1a' e 3a individuano un punto della curva.
Così anche 3a' e 1a, 1b' e 3b, 1b e 3b', procedendo fino al completamento dell'ellisse.

Costruzione di una parabola dati vertice e due punti

Tracciare l'asse focale a, individuare su esso il vertice V; in modo simmetrico rispetto l'asse a, segnare i due punti P noti della parabola.
Tracciare per V e i due punti P dei segmenti tali da generare un rettangolo inscrivente come da figura.
Segnare sul segmento passante per V, una serie di punti in figura 1, 2, 3, segnando quindi la metà e la metà della metà, ed avendo cura di usare una numerazione rovescia nel tratto di destra, in figura 3, 2, 1. Sui segmenti passanti per i punti P, segnare in modo analogo dei punti A, B, C. Congiungere questi ultimi con il vertive V. Tracciare dei segmenti paralleli all'asse a dai punti 1, 2, 3, 3, 2, 1, fino a rintracciare rispettivamente i segmenti AV, BV e CV, ottenendo gli altri punti della parabola.

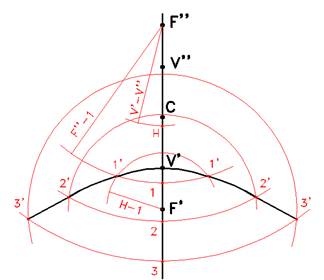Costruzione di un'iperbole - modo compatto

Tracciare l'asse focale, i vertici V' e V'' ed i fuochi F' ed F'', simmetrici rispetto al punto centrale C.
Registrare sul compasso la distanza tra i vertici V'-V'', e con tale apertura puntando in F'', tracciare un segno sull'asse che individua il punto H. Segnare ora sempre sull'asse dei punti 1, 2, 3, come da figura e a distanze arbitrarie. Puntare il compasso in F'' e tracciare delle semicirconferenze con aperture F''-1, F''-2, F''-3.
Registrare ora col compasso la distanza 1-H, puntare con tale apertura nel fuoco F', e tracciare un'altra semicirconferenza fino a rintracciare i punti 1' nelle intersezioni con la semicirconferenza di raggio F''-1.
Procedere con le aperture 2-H all'intersezione con F''-2 si trovano i punti 2', e via così ottenendo gli altri punti dell'iperbole.

Si consiglia, di infittire i punti 1, 2, 3 nei punti critici vicino al vertice dell'iperbole, avendo così maggior precisione di tratto.

Costruzione di un ovale

Tracciare un sistema di riferimento della figura, evidenziato in figura dall'asse a.
Segnare sull'asse un punto che chiameremo 1; puntare il compasso in 1 con apertura a piacere ma opportuna, descrivendo una circonferenza intera, incidente in un punto 2 l'asse a. Con medesima apertura puntare in 2 e descrivere un'altra circonferenza, la quale a sua volta torna ad incidere l'asse in 1, ed interseca la precedente circonferenza in due punti che chiameremo 3 e 4.
Tracciare dei segmenti passanti per 1-3, e per 2-3, fino a rintracciare i punti di tangenza T, come da figura. Ripetere l'operazione dal punto 4, con segmenti 4-1 e 4-2.
Puntare ora il compasso nel punto 3 con apertura 3-T, tracciando una porzione di circonferenza fino a raggiungere l'altro punto T. Ripetere l'operazione con medesima apertura (la figura è simmetrica), puntando in 4, e chiudendo così l'ovale.

Costruzione di un ovolo

Tracciare un sistema di riferimento della figura, evidenziato in figura dagli assi AB (maggiore) e CD (minore). Puntare il compasso al centro O di tali assi, e tracciare una circonferenza di raggio O-A, fino ad intersecare l'asse maggiore AB in un punto che chiameremo 1.
Tracciare una circonferenza con centro in 1 e raggio 1-B.
Tracciare due segmenti C-1 e D-1 prolungando fino a rintracciare su questa circonferenza i punti 2, come da figura.
Per ottenere i "fianchi" dell'ovolo, procedere come segue: individuare il punto M medio di AB; tracciare in A un segmento perpendicolare all'asse; puntare in A con apertura A-M e descrivere una semicirconferenza fino ad individuare i punti 3. Con medesima apertura puntare nei punti 3 e tracciare una porzione di circonferenza restando dentro la figura. Congiungere i punti 3 col punto B. Verranno a intersecarsi i punti 4. Per conferma, puntare in B con raggio OB.

Puntando in 4 con apertura 4-D e 4-C si completa l'ovolo con i tratti C-2 e D-2.

Costruzione di un poligono regolare generico

Tracciare un sistema di riferimento della figura, evidenziato in figura dagli assi AB e CD. Puntare il compasso al centro di tali assi, e tracciare la circonferenza in cui inscrivere il poligono. Puntare ora il compasso sia in A che in B con apertura A-B, ottenendo le intersezioni nei punti C e D.
Dal punto A, tracciare un segmento inclinato come in figura, e segnare il n numero di divisioni pari al numero di lati desiderato. Unire il punto B con l'ultima divisione del segmento (nel nostro caso 7), ed in maniera parallela, proiettare sull'asse AB i rimanenti punti; secondo il metodo di Talete, esso verrà così suddiviso in parti uguali. Tracciare dei segmenti facendo perno su C e D, passanti per le divisioni ottenute sull'asse AB, che incidano la circonferenza.
NOTA: Il numero di intersezioni è il doppio di quanto richiesto, si procede quindi ad un'opportuna cernita dei punti che contengono la figura prefissata.

Costruzione della spirale di Archimede dato il passo

Tracciare un asse a, e su di seeo un punto A.
Con apertura pari alla metà del passo, puntare in A e tracciare una semicirconferenza (*).
Scegliere uno dei due punti di intersezione con l'asse, in figura il punto B, e nominare l'altro a cifre col numero 1.
Puntare in B con apertura B-1 e realizzare la porzione di voluta dal punto 1 al punto 2.
Puntare in A con apertura A-2 e realizzare il tratto 2-3.
Puntare in B con apertura B-3 e realizzare il tratto 3-4.
Puntare in A con apertura A-4 per ottenere il tratto 4-5.

NOTA: il passo della spirale è regolare.

Costruzione di una spirale (a voluta jonica)

Tracciare un quadrato di vertici 1, 2, 3, 4. Prolungarne i lati come in figura, a creare degli assi non incidenti in una sola origine.
Puntare il compasso in 1 con apertura 1-4, tracciare un quarto di cerchio fino a rintracciare il punto A.
Puntare in 2 con apertura 2-A descrivendo un quarto di circonferenza fino a trovare il punto B.
Puntare in 3 con apertura 3-B tracciando un quarto di circonferenza fino a trovare il punto C.
Puntare in 4 con apertura 4-C tracciando un quarto di circonferenza fino a trovare il punto D.
Puntare in 1 con apertura 1-D tracciando un quarto di circonferenza fino a trovare il punto E.
Puntare in 2 con apertura 2-E tracciando un quarto di circonferenza fino a trovare il punto F.
NOTA: Nel '500 il Vignola studia questo metodo per descrivere le volute dei capitelli ionici.

Costruzione di una spirale (a conchiglia)

Tracciare un sistema di riferimento della figura, evidenziato in figura dagli assi a e b.
Tracciare dodici punti 1, 2, 3, 4.. a distanza di meno di un centimetro tra loro, e condurre per essi dodici circonferenze concentriche puntando il compasso all'origine degli assi.
Mantenendo l'apertura del raggio dell'ultima, col metodo della divisione dell'angolo retto, dividere la semicirconferenza superiore in sei parti, e come da figura, traguardando l'origine degli assi, tracciare deisegmenti tali da dividere il cerchio in dodici parti.
A partire dall'origine, individuare le intersezioni tra un segmento divisore e la prima circonferenza, segnarlo ed attribuire un numero, nel nostro caso 1'.
Passare al divisore successivo e scalare di una circonferenza, in figura punto 2'. Procedere fino a raggiungere il punto 12'=12. La crescita del passo della spirale in tal caso risulta essere progressiva.

Costruzione di una cicloide

Se osserviamo un punto di una ruota che procede spostandosi rotolando lungo una traiettoria, la curva descritta dal punto è detta cicloide, ed ha molteplici proprietà sia in matematica che in fisica.
Gli orologi a pendolo sfruttano proprio una sagoma a cicloide che contiene il movimento del cavo garantendo oscillazioni regolari e quasi permanenti nel tempo.

Tracciare un sistema di riferimento della figura, evidenziato in figura dalla porzione di retta contenente la serie dei centri O da 0 a 12, preferibilmente sopra la metà del foglio.
Su tale retta scegliere un segmento tale che la distanza tra O0 ed O12 abbia la stessa misura della circonferenza, pertanto stabilire un raggio e moltiplicare tale misura per 2π (2 x 3,141593 = 6,283185).
Dividere tramite il metodo di Talete tale segmento in 12 parti, individuando la serie di centri O.
Tracciare la prima circonferenza con centro in O0 e dividerla in 12 parti usando quattro volte il metodo della divisione dell’angolo in tre parti, ottenendo i punti indicati in figura con A, B, C, D, E, F, G, ed i simmetrici fino ad N.
Tracciare le linee di sviluppo, parallelamente al sistema di riferimento dei centri O, passanti per i punti: A, NB, MC, LD (coincide col sistema di riferimento), IE, HF, G.
Osserviamo il punto A: esso all’istante 0 è alla sommità della circonferenza di centro O0, pertanto costituisce il primo punto della cicloide A°, ma all’istante 1 la circonferenza di riferimento è quella di centro O1 ed il punto A si sarebbe spostato alla prima delle dodici divisioni, per intenderci in B.
Il secondo punto della cicloide A1 è quindi l’intersezione della seconda circonferenza con l’allineamento della seconda posizione, nel nostro caso NB.
Il terzo punto A2 è l’intersezione della circonferenza di centro O2 con l’allineamento MC.
Il quarto punto A3 è l’intersezione della circonferenza di centro O3 con l’allineamento LD.
Per concludere la cicloide si deve procedere con questo metodo fino al punto A12.

DISEGNO TECNICO
FONDAMENTI DI GEOMETRIA PIANA

Si comincia ad utilizzare i rapidograph eseguendo facili esercizi molto importanti sotto il profilo geometrico. Per convenzione, in rosso è riportato il pennino 0,2 ed in nero quello 0,4.

Costruzione della mediana di un segmento

Dato un segmento AB, tracciare con il compasso due porzioni di circonferenza puntando sia in A che in B con la medesima apertura, opportunamente maggiore della metà.
Le intersezioni 1 e 2 delle due porzioni di circonferenza individuano una retta mediana, ovvero passante per un punto M, medio, eqiuidistante dai punti A e B.
In geometria, A e B sono detti polari rispetto la mediana, che quindi è il luogo geometrico dei punti equidistanti da i poli

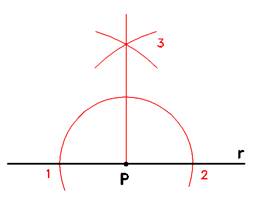Costruzione della perpendicolare in un punto

Data una retta r ed un punto P ad essa appartenente per cui si voglia trovare una perperndicolare, tracciare un semicerchio puntando il compasso nel punto P, ottenendo le intersezioni indicate con 1 e 2.
Puntando il compasso in 1 e 2 con apertura maggiore, si ottiene l'intersezione 3.
Congiungendo l'intersezione 3 con il punto P si ottiene una retta perpendicolare alla retta r nel punto P.

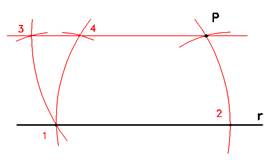Costruzione della parallela per un punto assegnato P

Data una retta r ed un punto P, segnare su r un punto 1, arbitrariamente scelto.
Tracciare con apertura 1-P una porzione di circonferenza fino ad intersecare r in un punto che chiameremo 2.
Senza mutare apertura, tracciare puntando in 2 (o in P) un'altra porzione di circonferenza. Questa passerà in entrambi i casi per il punto 1.
Registrare sul compasso la distanza 2-P, e con tale apertura riprodurre questa misura puntando in 1 il compasso. Verranno
così a generarsi i punti 3 (o 4), per i quali passa la retta parallela
ad r e passante per P

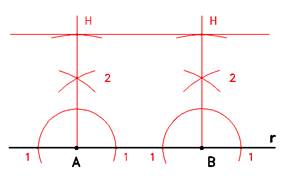Costruzione della parallela a distanza assegnata H

Data una retta r, scegliere arbitrariamente due punti A e B, opportunamente distanti.
Applicare il metodo delle perpendicolari (puntando in A ed in B il compasso ad apertura arbitraria, e generando due semicirconferenze; puntare nei punti 1 con apertura maggiore individuando i punti 2, per cui passano le perpendicolari alla retta r nei punti A e B.)
Registrare sul compasso la distanza prefissata e riportarla sulle perpendicolari fino a trovare i punti H, per i quali passa
la retta parallela alla retta r.

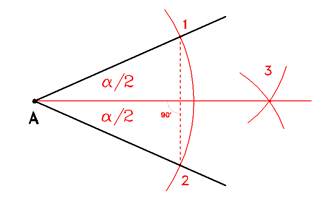La bisettrice

Dato un angolo a di cui si voglia trovare la bisettrice, puntare in A con apertura arbitraria, fino a trovare sulle rette che delimitano l'angolo a, i punti 1 e 2.
Con apertura maggiore, puntare sia in 1 che in 2 tracciando delle porzioni di circonferenza tali da intersecarsi individuando così il punto 3.
la congiungente tra A ed il punto 3 è detta retta bisettrice, in quanto divide l'angolo in due parti uguali.
NOTA: La bisettrice è anche mediana della corda 1-2 e dell'arco da essa sotteso.

Triangolazioni

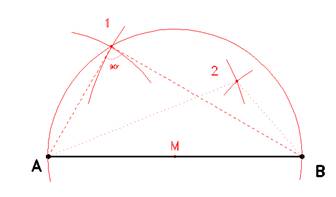
Per posizionare nel piano un punto (1 o 2) tale da formare un triangolo rispetto ad un segmento AB, ed essendo note le misure dei cateti, basti puntare in A con apertura pari ad un cateto, ed in B con la misura dell'altro. L'intersezione delle due circonferenze individuano in modo univoco il terzo punto.
NOTA: Nel caso dei triangoli rettangoli, è da notare come il terzo punto appartiene alla circonferenza di centro M (punto medio di AB), e di raggio AB/2.
NOTA: Nel rilievo architettonico, la triangolazione è l'unico modo valido per avere una perfetta riproduzione
delle reali disposizioni degli oggetti.

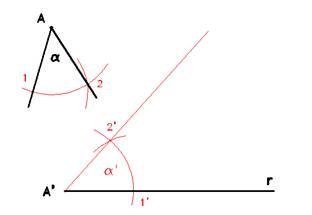Riproduzione di un angolo

Dato un angolo a ed una retta r sulla quale rintracciare il medesimo angolo, puntare il compasso con apertura arbitraria ed opportunamente ampia nel vertice A, intersecando in due punti che chiameremo 1 e 2.
Sulla retta r, segnare un punto A' e riprodurre la precedente apertura fino a rintracciare il punto 1'.
Tornando all'angolo a, registrare sul compasso la distanza 1-2, e riprodurla sulla retta r puntando in 1', trovado così il punto 2'.
La congiungente A'2' contiene rispetto a r la medesima porzione di piano di a.

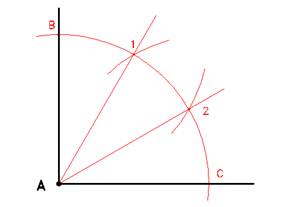Divisione di un angolo retto in tre parti

Dato un angolo retto, tracciare ad apertura arbitraria e puntando nel vertice A una porzione di circonferenza fino a trovare i punti B e C.
Con la medesima apertura puntare sia in B che in C ottenendo le intersezioni rispettivamente 2 e 1.
Le congiungenti A-1 ed A-2 dividono l'angolo retto in tre parti uguali da 30° ciascuna.
NOTA: i punti 1 e 2, dividono in tre anche l'arco, e le distanze B-1, 1-2 e 2-C sono uguali.

Costruzione delle tangenti ad una circonferenza

Data una circonferenza di centro C ed un punto esterno A da cui tracciare le tangenti, congiungere il punto A con il centro C (per individuare il centro, basti puntare in due punti della circonferenza con medesima apertura del suo raggio).
Tramite il metodo delle mediane rintracciare il punto medio M.
Con apertura M-C, puntando in M, tracciare una porzione di circonferenza tale da intersecare la circonferenza data in due punti che chiameremo T.
Le congiungenti A-T sono entrambe tangenti la circonferenza rispetto ad un punto dato.
Si noti come il triangolo ACT sia rettangolo in T, che quindi il raggio nel punto di tangenza sia sempre perpendicolare alla tangente.
Si noti anche che l'asse CA è mediana della corda TT e bisettrice dell'angolo di vertice in A.
Tangenti equatoriali si avrebbero se A giacesse all'infinito.

Il principio di Talete

Di notevole importanza per le fondamenta della geometria, nonchè della teoria della proiezione è il teorema di Talete.
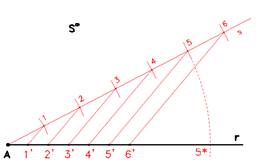Tracciare una retta r, e partendo da un punto A, tracciare una retta s arbitrariamente ed opportunamente inclinata rispetto ad r. Segnare dei punti ad intervalli regolari sulla retta s, in figura i punti 1, 2, 3, 4, 5, 6.
Scegliere un'inclinazione (*) e tracciare parallelamente tra loro dei segmenti passanti per i punti 1, 2, 3, 4, 5, 6, fino ad intersecare la retta r, generando le intersezioni 1', 2', 3', 4', 5'.
Si noti come le misure dei segmenti proiettati siano inferiori rispetto al vero (osservare 5' e 5*), ma anche che il rapporto delle loro distanze è costante, tutto per effetto della proiezione da una sorgente impropria S , posizionata all'infinito.

(*) tale inclinazione offre proiezioni non aberrate se parallela alla corda 5-5*, ovvero perpendicolare alla bisettrice dell'angolo contenuto tra r ed s.

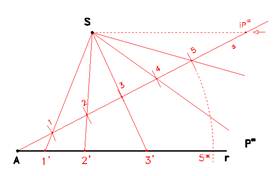
Il principio di Talete con sorgente propria

Proiettando da un punto proprio S gli intervalli 1, 2, 3, 4, 5, 6 sulla retta r, generando i punti 1', 2', 3', 4', .. noteremo una crescita progressiva delle distanze dovuta alla proiezione da sorgente propria.
NOTA: Nel caso di una sorgente propria S, le rette proiettanti non sono più parallele tra loro (fascio improprio), bensì convergenti nella sorgente prefissata (fascio proprio).
Se ne deduce che se la sorgente S si allontanasse all'infinito, allora il fascio proiettante diventa improprio e le rette proiettanti diventano tra loro parallele.
NOTA: Proiettando infine da S in maniera parallela ad r, rintracceremmo sulla retta s l'immagine di un punto P giacente all'infinito lungo la retta r.
A titolo informativo tali relazioni tra elementi di una proiezione sono dette corrispondenze.
NOTA: La vera posizione ad esempio del punto 5 su r si ottiene solo ribaltando il punto 5 rispetto il punto A, che in geometria è detto il punto unito, ottenendo così il punto 5*.

Fonte:

http://www.webalice.it/greendog/cs/files/disegno12.doc

http://www.webalice.it/greendog/cs/files/disegno11.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : Disegno tecnico geometria piana figure piane tipo file : doc

Clicca qui per non perdere altre informazioni utili e interessanti sul disegno tecnico

Disegno tecnico geometria piana figure piane