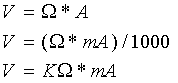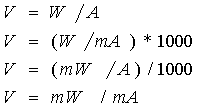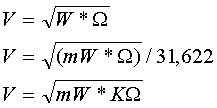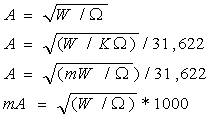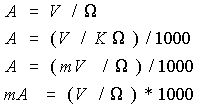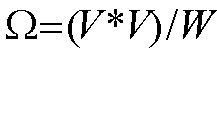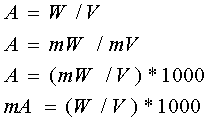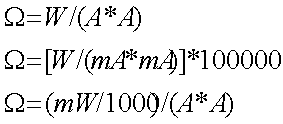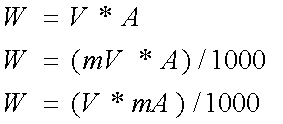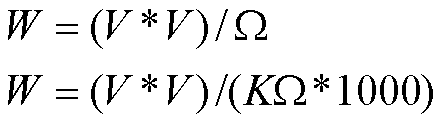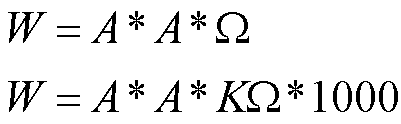Legge di ohm generalizzata
Legge di ohm generalizzata
La comodità di internet è quella di poter in qualsiasi momento chiedere , cercare e trovare qualsiasi informazione abbiate la necessità di conoscere, noi per farvi risparmiare tempo per attività più gratificanti abbiamo provveduto a selezionare i contenuti per noi più rilevanti ed esplicativi dal web per scopi didattici, conoscitivi e divulgativi, il nostro obiettivo è il progresso delle scienze e delle arti utili in quanto pensiamo che siano molto importanti per il nostro paese i benefici sociali e culturali della libera diffusione di informazioni utili.
Legge di ohm generalizzata
Verifica della legge di Ohm generalizzata
 |
Scopo della prova
Verifica sperimentale della legge di Ohm. |
Materiali
Due alimentatori, un multimetro, alcuni resistori di resistenza diversa |
|
Schema elettrico
Procedura
Per effettuare in pratica tale verifica consideriamo, ad esempio, il circuito mostrato nella figura 1. Nella prova da noi effettuata abbiamo utilizzato i seguenti componenti circuitali: un alimentatore da 12 V e quattro resistori da 0,5 W aventi rispettivamente i valori: R1 = 100 W, R2 = 270 W, R3 = 330 W, R4 = 100 W.
Nel vostro caso state impiegando:
E = _____ V; R1 = _____ W; R2 = ______W ; R3 = ______ W. ; R4 = ______ W.
Nel circuito di figura 1 possiamo leggere simultaneamente il valore della corrente che scorre nel circuito e le tensioni localizzate ai capi di ciascuna resistenza. Tuttavia risulta più pratico servirsi di un solo voltmetro spostando, di volta in volta, la posizione dei suoi puntali di misura. Essendo il circuito realizzato con le resistenze tutte poste in serie, la corrente è la stessa per tutte.
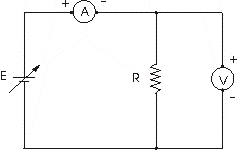
Fig. 1.
Iniziando la misura, non appena si dà tensione, nell'amperometro viene letta la corrente. Nel nostro caso risultava:
I = 150 mA;
Nel vostro montaggio il valore che leggete sull'amperometro è:
I = _______ .
Le tensioni da noi lette, mediante il voltmetro o i 4 voltmetri, sono risultate:
V1 = 1,5 V; V2 = 4 V; V3 = 4,9 V; V4 = 1,5 V.
Nel vostro montaggio avete ottenuto:
V1 = _______ V; V2 = _______ V; V3 = _______ V; V4 = _______ V.
La prima osservazione che si può fare è che V1 = V4 dato che le resistenze hanno lo stesso valore e sono collegate in serie.
La seconda osservazione e che la somma di tutte le cadute di tensione:
E = V1 + V2 + V3 + V4 = 1,5 + 4 + 4,9 + 1,5 = 11.9 V
Si discosta di un decimo di V dal valore teorico di 12 V. Tale differenza è dovuta agli errori di misura e di lettura degli strumenti.
Prof. Leonardo Mascellino
http://www.webalice.it/mascellino/Misure%20elettriche/Verifica%20della%20legge%20di%20Ohm%20generalizzata.doc
Legge di ohm generalizzata
Prima Legge di Ohm |
Il rapporto tra la d.d.p. V tra due punti di un conduttore metallico a temperatura costante e l'intensità di corrente che fluisce in esso è costante. R = V/i V = Ri (R = resistenza elettrica). I conduttori che seguono questa legge sono detti ohmici. [u.m.1e (Ohm)= 1V/1A] |
Seconda legge di Ohm |
A parità di ogni altra condizione, la resistenza R di un conduttore è direttamente proporzionale alla sua lunghezza e inversamente proporzionale alla sua sezione (u.m. emm2/m) |
Legge di Ohm generalizzata |
f = i (R+ri) dove ri è la resistenza interna |
La LEGGE DI OHM
Possiamo affermare che in un circuito elettrico se la differenza di potenziale applicata tra due suoi punti è uguale ad 1 volt e la resistenza parziale del tratto compreso tra questi due punti è di 1 Ohm in questo tratto circola la corrente di 1 ampere.
La legge di Ohm stabilisce in maniera molto semplice le relazioni esistenti tra le seguenti tre grandezze elettriche: tensione ( V ), Corrente ( I ) e resistenza (R)
Questa legge e stata enunciata dal famoso fisico tedesco George Simon Ohm ed è sicuramente la più importante fra quelle relative all'elettricità.
L'enunciato suona esattamente così: "L'intensità di corrente in un circuito è direttamente proporzionale alla tensione ad esso applicata ed inversamente proporzionale alla resistenza del circuito stesso". La sua espressione matematica è:
I = V / R
che permette di calcolare la corrente conoscendo la tensione e la resistenza. Da questa formula derivano:
V = I * R e R = V / I
che permettono di determinare la tensione o la resistenza quando siano note le altre due grandezze. Se al circuito è applicata una sola f.e.m. (forza elettromotrice) di valore E, vedremo che la formula della legge di Ohm si trasforma nella seguente:
I = E / (R +r)
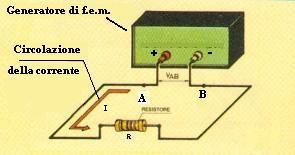
dove "r" è la resistenza interna dei generatore. Se consideriamo il circuito con un solo resistore e supponendo che la differenza di potenziale tra i morsetti A e B abbia il valore V, la corrente che circola nella resistenza R sarà:
I = V / R
Considerando invece il circuito con due resistori alimentato da un generatore di f.e.m. E e di resistenza interna r, se R1, ed R2, sono le resistenze esterne o di carico collegate in serie, avremo:
I = E / (R1 + R2 + r)
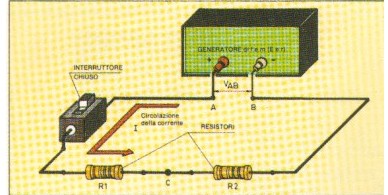
da cui si ricava E = I(R1 + R2 + r) = I R1 + I R2 + I r.
I prodotti I R1, I R2, ed I r (correnti per resistenze) esprimono rispettivamente le differenze di potenziale esistenti tra i punti (A C) e (C B), nonchè la caduta di tensione interna del generatore.
Possiamo constatare che la f.e.m. E applicata al circuito è uguale alla somma delle differenze di potenziale parziali, che vengono anche denominate "cadute di tensione".
Le cadute di tensione IR1 ed IR2, avvengono nel circuito esterno, e possono produrre un effetto utile. La caduta di tensione Ir avviene invece all'interno del generatore, e non ha nessuna utilità.
Supponiamo ora che l'interruttore sia aperto: nel circuito non circola corrente e, poichè I = 0, la caduta di tensione interna sarà nulla e la d.d.p. tra i due morsetti A e B del generatore sarà uguale alla f.e.m del generatore stesso: VAB = E.
Se invece il circuito viene chiuso e circola una corrente I, avremo tra A e B una differenza di potenziale (d. d. p.)
VAB = E - I * r
Un altro caso nel quale si verifica la condizione VAB = E si ha quando la resistenza interna del generatore è nulla (r = 0).
Anche se la maggior parte di noi conosce e sa correttamente usare la "Legge di Ohm", non dobbiamo dimenticare che ci sono persone alle prime armi che pur conoscendo l'esistenza di questa legge non sanno
utilizzarla nella pratica in modo da ricavarne il maggior vantaggio possibile.
Le formule che riporto potranno servire inoltre come promemoria per risolvere tutti quei piccoli problemi che si presentano giornalmente in campo elettronico.
OHM conoscendo VOLT e AMPER
 |
VOLT conoscendo AMPER e OHM
 |
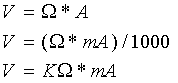VOLT conoscendo WATT e AMPER
 |
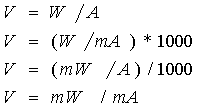VOLT conoscendo WATT e OHM
 |
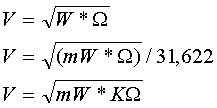AMPER conoscendo WATT e OHM
 |
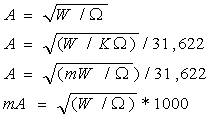AMPER conoscendo VOLT e OHM
 |
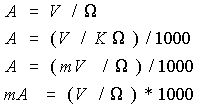OHM conoscendo VOLT e WATT
 |
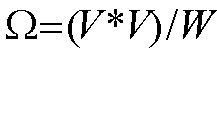AMPER conoscendo WATT e VOLT
 |
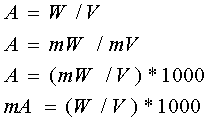OHM conoscendo AMPER e WATT
 |
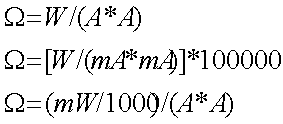WATT conoscendo VOLT e AMPER
 |
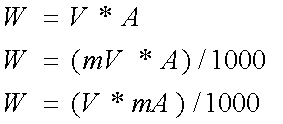WATT conoscendo VOLT e OHM
 |
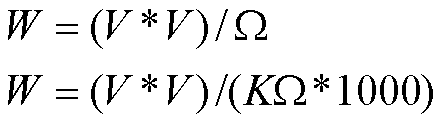WATT conoscendo AMPER e OHM
 |
|
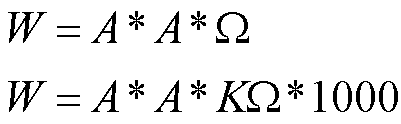Fonte: http://www.ilriparatore.it/pagine/teoria/ohm/ohm.htm
Legge di ohm generalizzata
Legge di ohm generalizzata
Legge di ohm generalizzata