Meccanica quantistica
Meccanica quantistica
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Meccanica quantistica
La crisi della meccanica classica e la nascita della meccanica quantistica
Primo colpo alla meccanica classica: Einstein (1905). La meccanica classica è una buona approssimazione della relatività quando le velocità in gioco sono basse rispetto a c.
Altri problemi però sorgono quando le dimensioni degli oggetti da descrivere sono molto piccole.
Al contrario della teoria della relatività, la meccanica quantistica ha molti padri e una lunga gestazione (all’incirca dal 1880 al 1930).
Avviene in questi anni una vera e propria rivoluzione del pensiero scientifico, che con moltissime applicazioni entra a fare parte della nostra vita quotidiana.
Gli oggetti di indagine sono molto piccoli (fotoni, elettroni ed altre entità che non verranno più chiamate ne’ onde ne’ corpuscoli, ma particelle)
La parola quanto indica una grandezza che varia in maniera discreta.
Tutto nasce da una serie di fatti sperimentali a prima vista non collegati tra loro, e che necessitavano di una interpretazione.
- Ancora esperimento di Young
interferenza di due sorgenti coerenti: interpretando la luce come un’onda si spiegano le frange di interferenza, ma ad un’osservazione più accurata si osservano fenomeni di granularità non spiegabili con la sola teoria ondulatoria.
In seguito si riuscì a ripetere l’esperimento con fasci di elettroni: anche in questo caso si ha interferenza!!
- Righe spettrali di emissione (Balmer, 1884)
l’idrogeno (e, in seguito, si scopre essere vero per tutti i gas), sottoposto ad una scarica elettrica, ha caratteristiche righe di emissione con lunghezze d’onda fissate, cioè emette solo luce di determinate frequenze.
Interpretazione delle righe di Balmer (e di Paschen, e di Lyman) quantificata da Rydberg :
con n1>n2 ed R costante di Rydberg.
Difficoltà: il modello atomico dell’epoca (plum pudding con elettroni immersi in un fluido positivo, o panettone di Thomson) non riusciva a spiegare tali spettri.
- Effetto fotoelettrico (Hertz, 1896; Lenard, 1900)
Il passaggio di corrente elettrica viene facilitato se il dispositivo sperimentale è illuminato (scoperta casuale di Hertz).
Più precisamente: quando la luce incide su una superficie metallica, l’energia cinetica degli elettroni estratti non dipende dall’intensità di luce incidente sulla lastra, ma dalla sua frequenza.
L’intensità è legata solo al numero di elettroni emessi, non alla loro energia cinetica. Interpretazione di Einstein (1905): l’energia non è assorbita con continuità, ma organizzata in pacchetti di energia (fotoni) assimilabili a vere e proprie particelle.
L’energia dei fotoni è quantizzata e vale E=hf .
- Corpo nero (Planck, 1900)
-pareti della cavità a T costante
-dimensioni del foro trascurabili
se freddo: la radiazione che entra non esce, per qualsiasi frequenza
se caldo: la radiazione emessa contiene tutte le frequenze
Secondo la termodinamica la potenza emessa è inversamente proporzionale alla lunghezza d’onda della radiazione (legge di Wien).
Aumentando T, il massimo di P si trova a lunghezze d’onda sempre minori, cioè ad alte frequenze.
Analogia con le onde su una corda e legge di Rayleigh-Jeans (ricavata da considerazioni termodinamiche):
!
Ipotesi di Planck: l’energia non può variare con continuità, ma solo in maniera discreta.
E=hf con h costante di Planck (h= 6,6 10-34 Js)
Secondo Planck la maggior parte dell’energia emessa dal corpo nero è causata da oscillatori di determinata lunghezza d’onda media; gli oscillatori a 
piccola anche, perché richiederebbero troppa energia per poter oscillare.
L’interpretazione di Planck non fu compresa se non come un artificio matematico per spiegare i dati sperimentali riguardanti P in funzione di 
e T.
La natura quantizzata dell’energia fu utilizzata poco dopo da Einstein per spiegare l’effetto fotoelettrico.
- Misura della massa dell’elettrone (Millikan, 1909)
noto il rapporto tra carica e massa dell’elettrone misurato da Thomson (1897), Millikan riuscì a misurare la massa dell’elettrone (caratteristica tipicamente corpuscolare).
La carica non è distribuita uniformemente nella materia, ma è quantizzata.
- Modello planetario dell’atomo (Rutherford, 1911)
l’atomo non è un plum pudding, ma ha un piccolo nucleo carico positivamente, e gli elettroni gli ruotano intorno. L’atomo è quasi del tutto “vuoto”. (osservare l’etimologia dalla parola atomo)
Però questo modello non può funzionare, perché si dimostra (EM) che un elettrone in orbita accelerata (centripeta) deve irradiare energia 
cadrebbe sul nucleo.
- Stati stazionari per gli elettroni nell’atomo (Bohr, 1913)
gli elettroni possono ruotare senza irradiare solo su determinata orbite, gli stati stazionari.
La frequenza della radiazione emessa (o assorbita) nel passaggio da uno stato stazionario all’altro vale 
- se
la radiazione è emessa sotto forma di fotone - se
.
A questo punto possiamo pensare all’interazione tra luce e materia come a un urto fotone-elettrone in cui energia scambiata: 
(vedi effetto Compton)
Altra conseguenza dell’atomo di Bohr: interpreta correttamente le righe di assorbimento e di emissione della spettroscopia (quantizzazione delle orbite elettroniche, fatto in chimica).
- Scattering fotone-elettrone (Compton, 1920)
conferma il dualismo onda-corpuscolo: i fotoni hanno sia natura ondulatoria (per es. sono diffratti, interferiscono) sia corpuscolare (urtano gli elettroni scambiando con essi energia e quantità di moto)
- Lunghezza d’onda associata ad una particella (De Broglie, 1924)
ipotesi di De Broglie: anche le particelle dotate di massa come gli elettroni presentano un doppio aspetto, corpuscolare e ondulatorio.
La loro lunghezza d’onda è: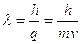
Ma dalla quantizzazione del momento angolare (Bohr) 
.
La situazione è analoga ad una corda vibrante con estremi fissati: ad ogni onda stazionaria corrisponde una lunghezza d’onda fissata, e dunque anche una frequenza ed un’energia fissata! Le onde stazionarie corrispondono ad energie quantizzate!
(relazione con matematica e musica)
- Relazione di indeterminazione (Heisemberg, 1926; Schrodinger, 1926)
era necessaria una matematizzazione che interpretasse tutti questi fenomeni che avevano in comune la quantizzazione. Vi giunsero (separatamente e con formalismi diversi) Heisemberg e Schrodinger nel 1926, gettando le basi formali della meccanica quantistica.
Visto che la meccanica classica funziona bene per oggetti “grandi”, i risultati della meccanica quantistica devono essere in accordo con la meccanica classica se applicati su scale dimensionali spazio-temporali grandi, o a corpi macroscopici (Bohr).
Concetto base: indeterminazione tra grandezze fisiche incompatibili:
Viene introdotta una funzione d’onda, tale che il suo quadrato è legato alla probabilità di trovare una particella in un certo stato. (cercare figure di orbitali su internet)
Ecco perché non si vedono mai immagini di atomi al microscopio: non è possibile! E per legge di natura, non per limiti tecnologici!!!
11. Critica di Einstein (1930)
famosa frase “Dio non gioca a dadi”; volendo confutare l’approccio probabilistico della meccanica quantistica, Einstein propose un esperimento ideale, che però fu chiarito da Planck proprio alla luce della teoria della relatività , e confermò la correttezza di tale approccio.
Es. 1 di Feynman
Es. 2 lunghezza d’onda di De Broglie di una pietra di massa 1 kg e velocità 1 m/s: 
E’ un valore così piccolo rispetto alle dimensioni degli atomi e anche dei nuclei, che non possiamo aspettarci alcun aspetto “ondulatorio” dalla pietra: non diffrange se passa attraverso una fenditura, non interferisce con altre pietre, ecc. Gli ostacoli che la pietra può incontrare sono molto più grandi della sua lunghezza d’onda, dunque valgono le usuali leggi della meccanica classica.
Es. 3 è possibile parlare di traiettoria (classica) di un elettrone in un atomo?
raggio 10-10 m 
l’indeterminazione sulla velocità è 1/10 della velocità della luce, e quindi non è possibile una descrizione classica del moto di un elettrone nell’atomo.
Es. 4 se A e B sono grandezze incompatibili e A è determinata, allora B è indeterminata, e ogni stato in cui A è determinata contiene tutti gli stati definiti dai possibili valori di B.
Cosa possiamo prevedere a priori circa il risultato della misura di B? Le probabilità dei diversi risultati possibili (secondo la meccanica classica avremmo detto che potevamo conoscere a priori il risultato della misura di B)
La logica della meccanica quantistica non è a due valori (vero/falso) ma a tre (vero/falso/indefinito ossia ne’ vero ne’ falso ma sovrapposizione di due stati).
- Paradosso EPR (x es. con con due fotoni a polarizzazione opposta)
La misurazione dello stato di polarizzazione di un fotone induce istantaneamente l’altro fotone ad avere polarizzazione opposta)
- Gatto di Schrodinger
Altri studiosi che svilupparono la meccanica quantistica: Pauli, Fermi, Dyson, Feynman (discorso sul progetto Manhattan)
Nel dopoguerra: manifesto per la pace di Russel (1955), firmato dai più importanti fisici dell’epoca.
Fonte: http://quattrobi.altervista.org/verda/meccanica%20quantistica.doc
Sito web da visitare: http://quattrobi.altervista.org/verda/
Autore del testo: non indicato nel documento di origine
Parola chiave google : Meccanica quantistica tipo file : doc
La meccanica quantistica, come abbiamo già accennato, è una nuova meccanica che è finalizzata a descrivere il moto dei corpuscoli di dimensioni atomiche e subatomiche. Essa non fa più uso delle leggi di Newton, ma di leggi probabilistiche, cioè di leggi tipicamente matematiche. Con la meccanica quantistica si viene quindi a separare nettamente la macrofisica dalla microfisica, riservando all'una e all'altra leggi, modi di operare e competenze specifiche.
Nel 1927, il fisico tedesco Max Born dette, alla funzione d'onda, un significato di tipo probabilistico. Egli introdusse il concetto di probabilità affrontando in modo del tutto originale il problema relativo alla posizione dell'elettrone intorno al nucleo atomico .
La forma attuale della meccanica quantistica è dovuta all'inglese P.A. Maurice Dirac (1902-1984). Essa si fonda direttamente sul principio di indeterminazione e trae le conseguenze di tale principio attraverso una struttura logica e matematica. La meccanica ondulatoria si colloca, all'interno della meccanica quantistica, come un suo aspetto particolare.
Fonte: http://www.ianua.com/patrizia/scuola/file/2H/atomo3corretto.doc
Sito da visitare: http://www.ianua.com/patrizia/scuola/
Autore del testo: non indicato nel documento di origine
Parola chiave google : Meccanica quantistica tipo file : doc
Visita la nostra pagina principale
Meccanica quantistica
Termini d' uso e privacy