Campo elettrico definizione

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Campo elettrico definizione

Il Campo elettrico

Definizione generale di campo

Immaginiamo di essere in una stanza e di misurare in ogni punto di essa con un termometro il valore della temperatura. In un determinato punto vicino alla finestra il termometro segnerà ad esempio il valore 18 °C, in un altro punto vicino al termosifone potrà segnare il valore 22 °C, in un punto in mezzo alla stanza indicherà ad esempio 21 °C. Avremo quindi una mappa completa del valore della temperatura all’interno della stanza: ossia, per ogni punto dello spazio all’interno di essa abbiamo associato il valore di una grandezza fisica (che in questo caso specifico è la temperatura ma può essere per esempio anche l’umidità, la pressione, ecc..). Si dice allora che abbiamo un campo di temperatura. Posiamo dare allora la seguente definizione generale di campo:

In una certa regione dello spazio si ha un campo se ad ogni punto possiamo associare il valore di una certa grandezza fisica.

In fisica i campi si dividono in due categorie:

Se la grandezza fisica che possiamo associare ai vari punti dello spazio è una grandezza scalare, ossia è rappresentata da un numero (es. temperatura, umidità, pressione), si ha un campo scalare.
Se la grandezza fisica che possiamo associare ai vari punti dello spazio è una grandezza vettoriale (es. campo magnetico, campo elettrico, campo gravitazionale, campo di velocità), ossia è rappresentata da un vettore, si ha un campo vettoriale. In questo caso si deve pensare (come vedremo meglio più avanti) che ogni punto dello spazio sia il punto di applicazione di un vettore avente una certa direzione, intensità e verso.
Un esempio semplice di campo vettoriale ci viene mostrato tutti i giorni in televisione quando durante le previsioni del tempo ci fanno vedere la carta dei venti: in alcuni punti della penisola italiana viene disegnata una freccia che rappresenta il vettore della velocità del vento; poiché ovviamente non è possibile prevedere la velocità del vento in ogni punto dell’Italia, ogni vettore indica grossolanamente la velocità con cui soffierà in una grossa regione. Se in teoria, tutti gli abitanti dell’Italia in uno stesso giorno e nella stessa ora si mettessero ciascuno in un diverso punto dell’Italia e misurassero direzione, verso e intensità del vento nel punto in cui si trovano, avremmo associato a circa 60 milioni di punti della nostra penisola (tanti sono gli abitanti italiani) la grandezza fisica velocità, e precisamente velocità del vento nel giorno xxx e all’ora xxx.
I campi gravitazionale, elettrici e magnetici sono invece più difficili da concepire, perché nelle regioni in cui sono presenti non c’è nulla di materiale, nulla che si possa toccare o vedere; essi sono presenti anche nel vuoto. Per esempio, la Terra genera un campo gravitazionale (di cui viene fornita una rappresentazione in figura 1) attorno a sé che si estende dalla regione immediatamente sopra la sua superficie all’infinito.

FIGURA 1

Concetto di campo per interpretare le forze a distanza

Dall’antichità fino ai tempi di Newton si pensava che le forze si originassero soltanto a seguito di un contatto. Il concetto primitivo di forza veniva infatti costantemente associato a una spinta, a una trazione o a un urto.

Questo modo di pensare incominciò a mutare solo dopo la teoria della gravitazione universale di Newton, secondo la quale tra due oggetti (come per esempio la Terra e la Luna) si può esercitare una forza (la forza gravitazionale, appunto) senza che vi sia tra loro un mezzo materiale che possa esercitare la funzione di supporto per la propagazione della forza. Ma nonostante il vuoto e l’enorme distanza, le due masse si “sentono”. Lo stesso Newton cercò di capire questo nuovo aspetto delle forze, senza però riuscirvi. Dopo Newton si cercò di giustificare i fenomeni di interazione gravitazionale mediante “un’azione a distanza” agente istantaneamente da un oggetto all’altro. Tuttavia, nei fisici del tempo suscitò qualche perplessità l’idea che una corpo faccia sentire il suo effetto lontano attraverso lo spazio, anche quando questo è vuoto, e questo idea probabilmente suscita una giusta perplessità anche in noi, visto che secondo il senso comune le forze dovrebbero agire per contatto diretto. Per cui, successivamente, per giustificare questo effetto occulto, fu inventato un ipotetico mezzo imponderabile, l’etere, che poteva penetrare ovunque in modo da riempire ogni corpo; così come un suono si può propagare solo attraverso un mezzo materiale, allo stesso modo si pensava che una forza si potesse trasmettere grazie alla presenza di questo mezzo materiale. La teoria dell’etere restò in voga per circa due secoli nonostante nessun esperimento fu in grado di verificarne l’esistenza; ma l’avvento della teoria della relatività segnò il suo definitivo abbandono.

In contrasto con la concezione newtoniana dell’interazione istantanea fra corpi, dopo il 1800 incominciò a farsi strada con Faraday il concetto di campo, che si affermò definitivamente con Maxwell. Secondo la teoria dei campi, ogni effetto fisico si propaga nello spazio con velocità finita. Cioè, se un certo fenomeno A che avviene in una certa posizione P_A causa un fenomeno B che avviene in una certa posizione P_B diversa da P_A, la causa A e l’effetto B non possono avvenire istantaneamente ma tra essi dovrà intercorrere il tempo necessario al “segnale” originato da A per arrivare in B. Questo discorso è ovvio se il “segnale” che parte da A e arriva in B è un oggetto materiale. Per esempio, è naturale che se un calciatore calcia il pallone verso il portiere, tra il fenomeno A “lancio del pallone” e il fenomeno B “parata del portiere” intercorre il tempo necessario al pallone per andare dal piede del calciatore alle mani del portiere. Meno ovvio invece è quando abbiamo a che fare con due corpi tra i quali agisce una forza di tipo gravitazionale o elettrica, forze che, lo ripetiamo, agiscono a distanza, cioè agiscono anche se nello spazio che separa i due corpi c’è il vuoto. Facciamo un esempio per capire meglio.

Supponiamo di avere due sferette cariche A e B, una positiva e l’altra negativa (lo stesso discorso varrà ovviamente se invece dell’interazione elettrica tra le due cariche abbiamo l’interazione gravitazionale tra due masse), separate da una lunga distanza. Supponiamo che la sferetta A sia collegata a un supporto isolante fissato al terreno, mentre la sferetta B sia collegata all’estremità di una molla collegata ad una parete. Il tutto è mostrato in figura 2.

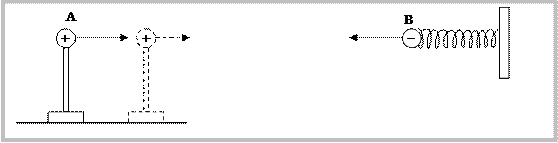
FIGURA 2

Poiché tra le sferette agisce una forza attrattiva, la molla sarà allungata di un certo tratto. Se improvvisamente diminuiamo la distanza tra le sferette spostando la sferetta A verso destra, con la nuova distanza più piccola della precedente la forza di attrazione diventerà più grande e perciò la molla dovrebbe allungarsi ancora di più e infatti così si osserva sperimentalmente. Ma ora poniamoci questa domanda: la molla inizia ad allungarsi nello stesso istante in cui viene mossa la sferetta A o con un certo ritardo? È più plausibile la seconda ipotesi, infatti, se la distanza iniziale tra le sferette è elevatissima, pare strano che la sferetta B senta subito il movimento di A; non è pensabile che la forza si trasmetta a velocità infinita, considerato che anche la luce, che è la “cosa” più veloce esistente in natura, impiega comunque un certo tempo per andare da un punto un altro. E infatti se eseguissimo questo esperimento realmente, così come altri analoghi, si osserverebbe che la sferetta B comincia a muoversi solo dopo un certo tempo dal cambiamento di posizione di A.

Allora, invece di interpretare un’interazione tra due corpi come un’azione a distanza (cioè istantanea) dell’uno sull’altro, la si interpreta utilizzando il concetto di campo. Consideriamo per esempio l’interazione gravitazionale e supponiamo di avere un oggetto di massa m che viene attratto dalla massa M della Terra. La teoria dell’interazione mediante il concetto di campo afferma che la presenza della massa M modifica in qualche modo lo spazio ad essa circostante, cioè dobbiamo immaginare che la massa M genera in ogni punto attorno a sé un “qualcosa”, che chiameremo campo gravitazionale, che in assenza della massa M non ci sarebbe. Ma la massa m si trova in un certo punto P nella zona circostante a M e anche nel punto P ci sarà il campo gravitazionale generato da M. Allora m subisce una forza non perché “sente” direttamente la presenza di M, ma perché “sente” la presenza del campo gravitazionale che M ha generato in quel punto. Un aspetto essenziale di questo punto di vista è che il campo generato da M nel punto P esiste indipendentemente dal fatto che in P si trovi o meno un’altra massa. La forza gravitazionale che agisce su una massa m posta nel punto P è dovuta al campo gravitazionale che lì già preesisteva e non a una diretta azione a distanza tra M e m.

Un’analogia può forse chiarire meglio il concetto fin qui esposto. Supponiamo di avere una membrana elastica, come quella dei tappeti elastici. Quando viene appoggiata sopra la membrana una certa sfera S₁ piuttosto grande, la membrana si modifica perché acquista una curvatura che prima non aveva. E se appoggiamo una sfera più piccola S₂ sulla membrana, vediamo che, proprio a causa della curvatura, cade verso la sfera più grande che occupa il centro di questa buca. Se non vedessimo la membrana elastica, ma solo la sfera piccola che si muove verso la grande, potremmo pensare che quest’ultima interagisca con la più piccola attirandola. Mentre, invece, non è così: la sfera piccola interagisce solo con la parte di membrana con cui è a contatto, e sono le caratteristiche di questa (curvatura) che la fanno muovere. In questa analogia, la membrana elastica curvata dalla sfera grande corrisponde allo spazio modificato dalla presenza della massa M. Quando vediamo una massa cadere diciamo che interagisce con la massa M della Terra che la attira, mentre, invece, sta interagendo solo con il campo gravitazionale generato dalla Terra nel punto dello spazio in cui si trova .

Quindi il concetto di campo elimina la necessità di pensare a una forza come qualcosa che agisce a distanza. E il concetto di campo permette anche di interpretare l’esperimento delle due sferette di figura 1: all’inizio, quando le due cariche sono ferme, il campo elettrico generato da A nel punto in cui si trova B è stazionario, nel senso che assume un certo valore costante nel tempo. Quando A comincia a muoversi, il campo da essa generato comincia a variare non dappertutto istantaneamente, ma varierà prima il campo dei punti vicini ad essa e poi via via quello dei punti sempre più distanti. Per fare un’analogia con questo fenomeno, supponiamo di essere su una barca su di un lago e di avere un dito che si muove con moto verticale alternativamente dentro e fuori dall’acqua in modo da produrre delle onde sulla superficie. Se ad una certa distanza da voi c’è un bastoncino che galleggia in superficie, esso, a causa del movimento del vostro dito, si muoverà periodicamente in su e giù. Così come il bastoncino si muove non perché “sente” direttamente la presenza del vostro dito ma sente ciò che ha provocato il vostro dito nel punto in cui il bastoncino stesso si trova (cioè le onde), anche la massa m non subisce una forza direttamente da M ma perché sente il campo che ha provocato M nel punto in cui si trova m. Se ad un certo punto volete far muovere il bastoncino con un’ampiezza di movimento maggiore, dovete muovere con un’ampiezza maggiore il dito. Ma il nuovo movimento del bastoncino non comincia nello stessi istante in cui variate il movimento del dito, ma solo dopo che la prima onda più grande di quelle precedenti lo investe, quindi con un certo ritardo; e un discorso analogo avviene anche nell’esperimento di figura 2.
Approfondimento: Concludiamo dicendo che, per quanto visto finora, anche se i campi non sono qualcosa che si può vedere o toccare, devono essere comunque pensati come entità reali, la cui creazione comporta un dispendio di energia da parte di chi ha generato il campo e alla cui presenza è sempre associata una certa quantità di energia. È a spese di questa energia, infine, che i campi inducono forze sui corpi di prova.

Definizione di campo elettrico

Supponiamo di disporre di quattro cariche elettriche Q₁, Q₂, Q₃, Q₄ in una regione di spazio vuota. Il discorso che segue vale però qualunque sia il numero di cariche presenti comunque siano disposte nello spazio. Si supponga che le quattro cariche rimangano fisse. Analogamente al caso del campo gravitazionale illustrato nel paragrafo precedente, possiamo pensare che la presenza di queste cariche abbia modificato in qualche modo lo spazio circostante, nel senso che ha generato attorno ad esse “qualcosa” che prima non c’era. Possiamo accorgerci di ciò dal fatto che, se mettiamo in un certo punto un pendolino caricato elettricamente, esso viene deviato in una certa direzione mentre non subiva nulla quando le cariche non c’erano (vedi figura 3).

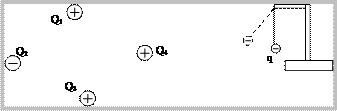
FIGURA 3

Diciamo allora che le cariche hanno generato nello spazio circostante un campo elettrico e le cariche si dicono cariche sorgenti del campo.

Vediamo allora come si fa punto per punto a misurare il campo elettrico. Se vogliamo conoscere il campo elettrico in un preciso punto P dello spazio, si pone in tale punto una carica di prova o carica esploratrice q positiva. Bisogna tener presente che il ruolo della carica q e delle altre cariche è profondamente diverso. Le cariche Q₁, Q₂, Q₃, Q₄sono le cariche che generano il campo mentre la carica q costituisce semplicemente lo strumento utilizzato per rivelare l’esistenza del campo; essa cioè svolge la stessa funzione che svolgeva il termometro nell’esempio del primo paragrafo. Se non c’è campo elettrico nel punto P la carica di prova non subisce alcuna forza, mentre se c’è campo elettrico essa subisce una forza 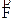cambierebbe), dal punto P in cui abbiamo posto la carica di prova (in un altro punto la forza sarebbe differente) e infine dal valore della carica q (se la carica di prova fosse più grande, anche la forza sarebbe maggiore). A questo punto si misura la direzione, il verso e l’intensità di questa forza (per esempio attaccando la carica di prova q ad un dinamometro). Si definisce il campo elettrico nel punto P come il rapporto:

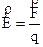
L’unità di misura del campo elettrico nel S.I. è il N/coulomb.

In figura 4 abbiamo schematizzato una misura del campo elettrico in un certo punto A dello spazio tramite una carica di prova in prossimità di sei cariche sorgenti.

FIGURA 4

Osserviamo innanzitutto che il campo elettrico è un vettore avente come direzione e verso in un determinato punto la direzione ed il verso della forza 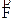che agisce su una carica positiva posta in quel punto. Inoltre una caratteristica importante è che esso dipende solamente dalle cariche sorgenti e dal punto P in cui lo abbiamo misurato ma non dalla carica di prova. Infatti l’esperienza dimostra che se nel punto P mettiamo una carica di prova doppia anche la forza da essa subita diventa doppia, cosicché il rapporto tra la forza e il valore della carica esploratrice rimane sempre costante.

Rimarchiamo inoltre il fatto che il campo elettrico in P esiste indipendentemente dal fatto che in P si trovi un corpo carico. La forza che agisce sulla carica q quando viene messa nel punto P è dovuta al campo elettrico che lì già preesisteva.

Osserviamo infine che, dato che anche la carica di prova stessa genera attorno a sé un campo elettrico, essa deve essere piccola rispetto alle cariche che generano il campo per non perturbare il campo preesistente che deve essere studiato.

Il campo elettrico si dice che è un campo di forze perché se dentro di esso viene posta una carica su di essa si manifesta sempre una forza.

Una curiosità sul campo elettrico è che un gran numero di creature acquatiche producono campi elettrici, per esempio le anguille elettriche possono generare campi elettrici abbastanza potenti da uccidere piccoli animali e stordire animali più grandi, compreso l’uomo. Gli squali sono conosciuti per la loro capacità di sentire deboli campi elettrici presenti nelle loro vicinanze grazie a organi specializzati.

Campo elettrico generato da una carica puntiforme

Ci proponiamo ora di trovare il campo elettrico generato da una carica sorgente Q in un punto P a distanza r. Supponiamo che la carica Q sia positiva. Se poniamo in tale punto P una carica di prova q positiva, essa subirà una forza diretta come in figura 5.

FIGURA 5

Sappiamo anche il valore di tale forza, poiché basta applicare la legge di Coulomb:

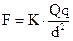
Per trovare il valore del campo elettrico basta ora dividere per q:

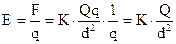
La direzione è quella della retta individuata dal punto in cui si trova la carica Q che genera il campo e dal punto P in cui si misura il campo, mentre il verso è rivolto da Q a P. Come si vede dalla formula, l’intensità del campo elettrico non dipende dal valore della carica di prova, ma dipende soltanto dal valore della carica che genera il campo e dalla posizione del punto in cui vogliamo determinarlo.

Se invece la carica Q che genera il campo è negativa, la direzione e l’intensità del campo nel punto P rimangono invariati, mentre il verso è rivolto da P a Q, come mostrato in figura 6.

FIGURA 6

Nella figura 6a è rappresentato il campo elettrico generato da una carica puntiforme positiva in diversi punti attorno a essa, mentre nella figura 7b è rappresentato il campo elettrico generato da una carica negativa.

FIGURA 7a FIGURA 7b

Come si vede, il campo elettrico in ogni punto è radiale rispetto la carica che genera il campo, cioè la retta su cui giace il campo passa sempre su tale carica.

Esempio:
Supponiamo di voler determinare direzione, verso e intensità del campo elettrico generato da una carica Q = + 6 · 10^-6 C in un punto situato a una distanza d = 5 cm da essa, come rappresentato in figura.

La direzione e il verso saranno quelli indicati in figura (se la carica Q fosse stata negativa il campo elettrico avrebbe avuto stessa direzione ma verso opposto) mentre l’intensità avrà il valore:

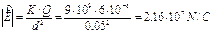
Campo elettrico generato da due o più cariche puntiformi

Supponiamo di avere un certo numero di cariche puntiformi che rimangono fisse nello spazio. Esse generano in ogni punto dello spazio attorno a se stesse un campo elettrico. Supponiamo di voler determinare quindi il campo elettrico in un certo punto P.

L’esperienza dimostra che vale il principio di sovrapposizione dei campi, in base al quale, se 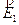, … sono i campi che le singole cariche Q₁, Q₂, …. genererebbero nel punto P in assenza delle altre, il campo elettrico risultante quando esse sono presenti contemporaneamente è dato da:

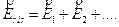
Vediamo di chiarire il concetto con un esempio. Supponiamo di voler determinare il campo elettrico generato da tre cariche puntiformi Q₁, Q₂, Q₃ in un certo punto P, come mostrato in figura 8.

FIGURA 8

I campi elettrici 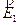che genererebbero rispettivamente le cariche Q₁, Q₂, Q₃ nel punto P se ciascuna di esse fosse presente da sola sono mostrati in figura (con le lunghezze proporzionali alle intensità). Il campo elettrico risultante sarà allora la somma vettoriale di questi tre campi.

Campo elettrico all’interno di un condensatore

Si può dimostrare che il campo elettrico tra due piastre piane di un condensatore carico ha dappertutto la stessa direzione (perpendicolare alle piastre), la stessa intensità e lo stesso verso, come mostrato in figura 9.

FIGURA 9

Dal campo elettrico alla forza agente su una carica

Se conosciamo il campo elettrico in un determinato punto dello spazio, possiamo trovare la forza che subisce una qualsiasi carica q se posta in quel punto. Basta applicare la formula:

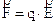
Non dimentichiamo che essa è una formula vettoriale, per cui essa ci dice che se metto in quel punto una carica positiva essa subisce una forza avente lo stesso verso di 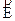(figura 10b)

FIGURA 10a FIGURA 10b

Rappresentazione del campo elettrico mediante le linee di campo

Per visualizzare il campo elettrico da un insieme di cariche, possiamo tracciare una serie di vettori in diversi punti dello spazio. Essi devono avere la direzione, il verso che ha il campo elettrico in ciascuno di quei punti e lunghezza proporzionale alla sua intensità, come abbiamo fatto nelle figure 7a e 7b. Tuttavia, questa rappresentazione è poco conveniente, perché se 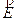è disegnato in un grandissimo numero di punti, la rappresentazione diventa molto confusa. Per questa ragione si preferisce di solito usare un altro sistema di visualizzazione, basato sulle linee di campo (dette anche linee di forza, anche se questa dicitura non è del tutto appropriata).

Per costruire una linea di campo dobbiamo procedere nel seguente modo:

si parte da un punto P₁ e si considera il campo elettrico 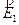presente in quel punto
A partire da tale punto P₁, ci si sposta di un piccolo tratto rettilineo ΔS₁₂ lungo la direzione e il verso indicati da 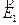arrivando quindi in un nuovo punto P₂ molto vicino a P₁ (più il tratto di cui mi sposto è piccolo e quindi più sono vicini P₁ e P₂ e più la costruzione della linea di forza è precisa)
Si considera quindi il campo elettrico 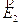presente nel nuovo punto P₂
Si ripete la stesso procedimento descritto nel punto 2, cioè ci si sposta di un piccolo tratto rettilineo ΔS₂₃lungo la direzione e il verso indicati da 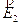fino ad arrivare ad un nuovo punto P₃.

La procedura può continuare così fino a che la linea di campo non incontra una carica. Il tutto è rappresentato in figura 11.

FIGURA 11

Alla fine di ciò avremo una linea continua costituita dall’insieme di tanti piccoli tratti rettilinei; se i tratti li costruiamo molto ma molto piccoli in pratica la possiamo considerare una linea continua “dolce”, cioè senza spigoli. Notiamo anche che dobbiamo disegnare con una freccia il verso della linea, che non è altro che il verso seguito nel costruirla. Per costruire un’altra linea di campo basta ripetere la procedura descritta sopra partendo da un punto qualsiasi non appartenente alla linea di campo già costruita. Le linee di campo ricoprirebbero completamente lo spazio che è sede di un campo elettrico; infatti in ogni punto dello spazio è definito il vettore campo elettrico. Tuttavia, per poter rappresentare il campo, occorre adottare un criterio che consenta di disegnare un numero limitato di linee di campo; generalmente, si stabilisce che il numero di linee di campo che attraversano una superficie unitaria sia proporzionale all’intensità del campo. Ne consegue che, nelle zone in cui le linee sono più rade, il campo è meno intenso.

È bene ricordare che le linee di campo non corrispondono a qualche cosa che esiste nel mondo reale. Esse sono solo un’efficace rappresentazione di come il campo varia in una data regione dello spazio.

Sperimentalmente le linee di campo si possono visualizzare distribuendo in un recipiente pieno di un liquido denso e fortemente isolante (per esempio olio di ricino) del semolino, frammenti di fibre sintetiche o semi d’erba e immergendo nel liquido i corpi carichi. I granelli di semolino, sotto l’azione delle forze elettriche, diventano dei dipoli elettrici che si distribuiscono lungo le linee di campo. La figura 12a rappresenta le linee di campo del campo generato da due cariche dello stesso segno e la figura 12b mostra come si vedono sperimentalmente. Le figure 13 a e 13 b sono analoghe ma per il caso di due cariche di segno opposto.

FIGURA 12a FIGURA 12b

FIGURA 13a FIGURA 13b

Dalla procedura che occorre seguire per costruire una linea di campo possiamo dedurre le seguenti caratteristiche delle linee di campo:

Sono costruite in modo che in ogni punto il campo elettrico è tangente alla linea di campo che passa per quel punto ed inoltre il verso di percorrenza della linea di campo corrisponde a quello del campo elettrico.
Se mettessi una carica positiva esploratrice ferma in un certo punto, essa inizierà a muoversi con una velocità iniziale tangente alla linea di campo che passa per quel punto. In generale le linee di campo del campo elettrico non coincidono con le traiettorie percorse da eventuali cariche elettriche poste in esso; infatti una linea di campo può risultare curva e una carica, per poterla percorrere, deve essere soggetta a una forza centripeta, cioè diretta verso il centro di curvatura, mentre invece è soggetta alla forza elettrica che è tangente alla linea stessa. Se la linea di campo è rettilinea, come nel campo radiale generato da una singola carica puntiforme, allora essa coincide con la traiettoria di una carica puntiforme posta nel campo elettrico con velocità iniziale nulla.
Il verso delle linee di campo è tale che esse escono dalle cariche positive ed entrano nelle cariche negative, oppure non terminano e si estendono all’infinito.
Sono sempre perpendicolari alle superfici di un conduttore, perché, se ci fosse una componente tangenziale del campo elettrico all’interno del conduttore, le cariche dentro di esso si muoverebbero. Ma ciò non può essere perché, dal momento che il conduttore riceve cariche in eccesso, esse, dopo un certo tempo in cui si dispongono in un certo modo dentro il conduttore, non si muovono più, altrimenti avremmo un movimento continuo di cariche.
Non esistono linee chiuse su se stesse (cosa che invece succede per le linee del campo magnetico).
Le linee di campo non si intersecano mai l’una con l’altra. Infatti se ciò avvenisse, significherebbe che nel punto in cui si incrociano due linee il campo elettrico avrebbe due differenti direzioni e ciò è impossibile.
Devono essere tracciate in modo che il numero di linee che attraversano una superficie di area unitaria perpendicolare ad esse sia proporzionale all’intensità del campo; per questo motivo si ha anche che il numero di linee che escono da una carica positiva o entrano in una carica negativa è direttamente proporzionale alla carica.

Nei Principia di Newton si legge: “Ma finora non sono riuscito a scoprire la causa di quelle proprietà della gravità…non avanzo ipotesi (hypotheses non fingo)…è sufficiente che la gravità esista realmente, agisca secondo la legge che abbiamo spiegato, e basti a spiegare tutti i moti dei corpi celesti…”

Fonte: http://www.webalice.it/paolocesaretti/appunti/campo_elettrico.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : Campo elettrico definizione tipo file : doc

Campo elettrico definizione