Campo magnetico

 

 

 

Campo magnetico

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

IL CAMPO MAGNETICO

 

Il campo magnetico è ciò che viene generato da un magnete. Il magnete ha polarità nord e sud, i poli di segno opposto si attraggono e quelli dello stesso segno si respingono (fig.1).
A differenza delle cariche elettriche, che sono isolabili, le cariche magnetiche non possono essere prese singolarmente (fig.2).

In figura 2 si osserva che i magneti pur essendo stati divisi continuano a mantenere
le polarità magnetiche nord e sud.
Ciò che permette ai magneti di attrarsi e di respingersi è l'interazione che avviene tra essi.

 

La forza che esiste tra i magneti si può calcolare con la seguente formula :
Fm=m1*m2*k*µ  ;
d²

• la Fm è la forza,
• m1 e m2 sono le masse dei due magneti,
• d è la distanza tra questi,
• k è una costante,
• µ è la permeabilità magnetica.

La permeabilità magnetica è data dalla seguente formula:
µ=µ0·µr ;
-µ0 è la permeabilità nel vuoto (4π·10^-7 H/m),
-µr è la permeabilità relativa del mezzo.
L'induzione magnetica B è uguale al rapporto tra la forza Fm di attrazione-repulsione
e la massa subente m :
B=Fm     [T]  Tesla
....m

 

Il flusso del campo magnetico Φ è la quantità di induzione magnetica che attraversa una superficie ortogonale al flusso stesso, la formula per  calcolare il flusso :
                                         Φ=B·S   [W] Weber
Il campo magnetico si può calcolare tramite la formula:
                                          H=B         
                                               µ              

A questo punto, osservando la formula della permeabilità magnetica si arriva facilmente alla conclusione che µ è costante; poiché µ0 è una costante e il mezzo conosciuto ha la propria permeabilità.
In realtà µ varia seguendo un ciclo di         isteresi.

Nella figura si osserva la curva di prima magnetizzazione (in rosso) dove alla fine c'è il punto di saturazione che corrisponde al momento in cui il materiale è completamente magnetizzato. Il punto di saturazione è definito da Hmax.
Il ciclo continua cambiando “strada” , dopo la prima magnetizzazione non è possibile tornare al punto in cui sia il campo magnetico H che l'induzione magnetica B siano zero.

         INTERAZIONE TRA CAMPI MAGNETICI

Esistono due tipi di interazione:

• Interazione diretta.
• Interazione a distanza.

L'interazione diretta esiste solo quando c'è un contatto tra due oggetti, per esempio quando si scrive con una matita su un foglio di carta, mentre nell'interazione a distanza gli oggetti non hanno bisogno di un contatto fisico, per esempio quando con una pistola si spara un proiettile e quest'ultimo colpisce un bersaglio, la pistola interagisce con il proiettile e il proiettile interagisce con il bersaglio; indirettamente la pistola ha interagito con il bersaglio (interazione a distanza).
Questo esempio di interazione a distanza è dato però da due interazioni dirette, invece nell'interazione a distanza tra due magneti è il campo magnetico che agisce su di essi.
Per avere presente cosa accade si può fare un semplice esperimento:
legando su dei carrelli due magneti ed essendo a conoscenza della loro magnetizzazione, a seconda della disposizione dei magneti si osserverà in modo migliore l'avvicinamento o l'allontanamento.
Il campo magnetico oltre a ruotare intorno alle calamite prese singolarmente va anche a racchiudere insieme le due calamite; il campo magnetico tende a far avvicinare il nord e il sud in modo che siano uno di fronte all'altro e ogni millimetro di spostamento dei carrelli fa si che il campo magnetico che racchiude le due calamite sia più forte, quindi le calamite si avvicinano con velocità sempre maggiore fino a toccarsi.

Nel caso contrario i magneti si oppongono a vicenda e in questo modo si allontanano, più sono lontani minore è la forza con cui il campo magnetico li spinge, così i magneti rallentano fino al punto in cui, senza più contatto significante tra i campi magnetici, si fermano.
L'interazione attraverso campi magnetici avviene anche senza la presenza di due magneti, per esempio ponendo un magnete nelle prossimità di un chiodo di ferro appeso ad un filo; si potrà osservare che il chiodo si posizionerà in modo da seguire le linee di forza del campo magnetico, questo fenomeno si può osservare in modo migliore ponendo una calamita sotto un vetro e spargendo sopra quest'ultimo della limatura di ferro che subito si disporrà in modo da formare le linee del campo magnetico.

Un altro esempio di interazione dei campi magnetici fu osservato da Faraday,

che nel 1831 quando scoprì che una variazione del campo magnetico che investe un filo conduttore può indurre in esso una corrente elettrica, questa variazione del campo magnetico è data dallo spostamento di un magnete in modo perpendicolare rispetto al filo conduttore.

Il fenomeno inverso fu osservato invece da Hans Christian Oersted.
Tempo prima, aveva appoggiato su di un tavolo, una lattina, ne collegò i poli con un filo di platino ed avvicino ad essa un ago magnetizzato.
L'ago avrebbe dovuto orientarsi nella direzione nord-sud, invece l'ago realizzò un mezzo giro di rotazione e si fermò perpendicolarmente al filo di platino.
All'inizio Oersted pensò che la rotazione dell'ago fosse dovuta alle correnti d'aria prodotte dal filo di platino riscaldato a causa del passaggio della corrente.
Per verificare questa supposizione interpose, fra l'ago ed il filo di platino, un pezzo di cartone. Il cartone aveva il compito di arrestare le eventuali correnti d'aria.
Rifece allora l'esperimento: l'ago si comportava allo stesso modo, quindi la presenza del cartone non modificava la deviazione dell'ago magnetico.
La relazione fra corrente elettrica e deviazione dell'ago poteva forse dipendere dalla direzione della corrente?
Oersted, in base a questa domanda, ruotò la lattina di 180° invertendo le polarità ai capi del filo di platino. La corrente nel filo aveva ora un flusso nella direzione contraria. Anche l'ago ruotò di 180° in direzione opposta a quella precedente. Il nord dell'ago si orientò nella direzione in cui prima era orientato il polo sud.
Doveva certamente esserci una interazione tra l'ago magnetico e le cariche elettriche in movimento ed inoltre la direzione della corrente elettrica, che fluisce nel filo, influenza l'orientamento dell'ago magnetico, ma non aveva identificato che genere di forza era e sulla base dei precedenti esperimenti di Faraday arrivò alla conclusione che una corrente elettrica che circola in un filo conduttore genera a sua volta un campo magnetico.

 

Ampere si concentrò invece sulle forze agenti tra fili percorsi da corrente che, come si osserva in figura 5

 

i fili che sono percorsi da correnti che fluiscono nella stessa direzione creano dei campi magnetici, conoscendo la regola della mano destra noi possiamo capire in che direzione va il campo magnetico di ciascuno dei fili e considerando che il campo magnetico va da nord a sud si può arrivare alla conclusione che il campo magnetico inizia da un estremo di un filo e arriva dalla parte opposta dell'altro filo facendo così avvicinare i due fili. Nel caso contrario, cioè nel caso in cui i due fili sono percorsi da correnti di direzione contraria, i fili si allontanano.

Esempi di interazione attuali
Tra i cellulari e i telefoni quando ci sono troppe telefonate su una “linea” capita che non si riesca a parlare con la persona che sta dall'altro capo del telefono, questo accade perché le onde elettromagnetiche dei telefoni cellulari si sovrappongono.
Un fenomeno interessante è quello che si può osservare mettendo un Compact Disk
(CD-Rom) o qualche oggetto in metallo, in particolare dorato, in un microonde; si osserverà che all'inizio si formeranno delle scintille dopodiché l'oggetto prenderà fuoco.

Il CD-ROM si presenterà così ( dopo il “trattamento” )
Un esempio più in grande di interazione tra campi magnetici è il treno a levitazione magnetica il funzionamento non è poi così complicato:
ora prendiamo come esempio questo pezzo di ferro , esso può scorrere all'interno del tubo di vetro.

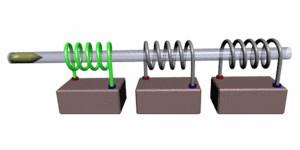
Dando corrente al primo dei solenoidi il pezzo di ferro inizierà a scorrere ,

 quando il pezzo di ferro si troverà all'interno del primo solenoide si toglierà la corrente a questo e si darà corrente al secondo ,


la stessa cosa si farà quando il pezzo si troverà all'interno del secondo solenoide ,

 

a questo punto siamo arrivati alla fine del nostro tubo di vetro , ma in un treno a lievitazione magnetica la corsa sarebbe proseguita.
Immaginiamo ora di dover fermare il treno: per  fermarlo basterebbe continuare a dare corrente al solenoide dentro al quale si trova il pezzo di ferro.

 

Bibliografia
Elettromagnetismo, edizioni masson parte II di: Piero Caldirola, Marcello Fontanesi, Elio Sindoni.
Elettricità e magnetismo: edizioni zanichelli parte I e II.
La ricerca: il campo elettromagnetico, edizioni loescher di Giovanna De Sabbata.
Elettromagnetismo edizioni ETAS libri di Joseph A. Edminister.
SITOGRAFIA
google web: come diventa un CD-ROM nel forno a microonde
google immagini: Faraday, Oersted, Ampère, magneti, magnetismo.

 

 

INTERAZIONE
TRA
CAMPI MAGNETICI

 

 

Autore del testo:   Daniele Matteo  & David Grifoni

fonte: http://www.itismeucci.it/meucci/wiky.nsf/d4481271ed965acfc125711c002d9f98/a7abfefbc8ee324ac12574550037c5be/$FILE/ATTSZ2FQ.doc

 

---

 

Campo magnetico

 

IL CAMPO MAGNETICO

 

Non tutte le sostanze hanno proprietà di magnetizzarsi: solo sostanze ferromagnetiche (ferro, acciaio, cobalto, nichel,...). Magnetite è minerale di ferro che ha proprietà magnetiche. Calamita rettilinea genera nello spazio circostante un campo di forza (quindi un campo vettoriale), ke chiamiamo campo magnetico. Un ago magnetico subisce una forza xke sente l’azione del campo magnetico generato dalla calamita. Poli: centri di forze magnetiche. X vedere se c’è un campo magnetico mettere un magnete e vedere se su di lui agisce forza. Direzione e verso di un campo magnetico in un suo punto sono la direzione e il verso della retta orientata ke va dal polo Nord al polo Sud di un ago magnetico ke sia in equilibrio in quel punto. Definite queste due componenti si possono definire le linee di campo che sono chiuse (v. esperienza cartoncino e limatura di ferro).

Campo elettrico ≈ a campo magnetico
-entrambi campi vettoriali (linee di campo)
-due poli (positivo e negativo)
Campo elettrico ≠ a campo magnetico
-per determinare linee di campo si usa carica positiva x il campo elettrico; si usa un ago                magnetico per il campo     magnetico
-possibile divisibilità dei poli per il campo elettrico; spezzando una calamita invece se ne  formano altre due

L’esperienza di Oersted (quella col bavoso):
(ago si sposta generando corrente nel filo)→Con esperienza Oersted concluse ke una corrente elettrica genera nello spazio circostante un campo magnetico. Quindi altro modo x trovare linee di campo: regola della mano dx in cui pollice è verso del campo elettrico mentre dita (chiuse nel pugno) indicano linee di campo (direz e verso).

Campo magnetico influenza non solo i magneti ma anke i conduttori xcorsi da corrente elettrica: quindi tra i due deve esistere una forza.
Esperienza di Ampere:
mettiamo due fili (l1 e l2) percorsi da corrente elettrica (I1 e I2) con distanza d e se I1 ha stesso verso di I2→fili si attraggono se no repulsione. Forza tra fili dipende da d e I.
F= K* I1*I2*l/d                   K=μ0/2п
μ0: costante di permeabilità magnetica nel vuoto
1 A è l’intensità di corrente ke, circolando in due fili rettilinei molto lunghi, paralleli e posti alla distanza di 1 m, esercita una forza di 2 X 10-7 N su ciascun tratto di filo lungo 1 m.
Come le cariche elettriche interagiscono mediante il campo elettrico le correnti elettriche interagiscono mediante il campo magnetico.

Materia costituita da cariche in moto: un atomo può essere descritto come un microscopico circuito percorso da corrente ke genera un campo magnetico. Gli atomi di un pezzo di ferro non magnetizzato sono orientati a cazzo (danno una risultante nulla), quando invece si magnetizza la maggior parte degli atomi si orienta verso una determinata direzione. Polarizzazione magnetica: tendenza all’ordinamento dei campi magnetici atomici.

Per misurare l’intensità si usa un filo prova e forza misurata su filo dipende da orientazione (filo ┴ a direzione campo). Allora forza direttamente proporzionale alla lunghezza e alla corrente I che lo attraversa:
F=B*I*l*senα (se ┴ sen=1)
B è il fattore ke moltiplicato per I e per l consente di trovare F, e varia proporzionalmente alla forza ke il filo di prova subisce da parte del campo magnetico e infatti B= F/Il   B= intensità del campo magnetico in un punto dello spazio
F= la forza ke subisce il filo, attraversato dalla corrente I, ke è  ┴ a linee di campo magnetico.
B=N/A*m=Tesla [T]

Se conduttore obliquo rispetto a linee di campo, ciò ke determina forza non è B, ma la sua proiezione nella direzione perpendicolare al flusso della corrente→ F= B┴Il. Direzione F ┴ B e ┴ I. Pollice parallelo a I, F esce ┴ dal palmo, dita parallele a B.

Quindi BIl= K* I1*I2*l/d →B= μ0/2п*i/d     (quindi B direttamente proporzionale a i e inversamente a d)            

La forza di Lorentz:
La forza del campo magnetico sul filo è la somma vettoriale delle forze ke lo stesso campo magnetico esercita sui singoli elettroni in movimento. Basta dividere la F risultante per il numero di elettroni di conduzione presenti in un tratto del filo: Fe = B┴Il/nAl= B┴I/nA                                      nAl= n° e- nel tratto di filo ke si considera
Stante ke I= enAv in cui v è la vel media degli elettroni e e è la carica degli elettroni→
Fe = B┴enAv/nA= ev B┴

Quindi notiamo ke F proporzionale a carica particella, sua vel e componente campo magnetico. Direzione e verso (mano dx) della forza su ciascun e- sono gli stessi della forza risultante sul filo.
Forza di Lorentz: Fq=qv B┴ (anke * senα)

Discriminatore di velocità:
In un condensatore in cui cariche negative sono sopra, un elettrone subirà una forza Fe rivolta verso il basso. Aggiungendo un campo magnetico al campo elettrico è possibile far passare gli e- con una data v in un foro posto all’estremità del condensatore (v. fig 10.4 pag. 214). Questo xke Fe è contraria a Fq quindi se le due forze sono uguali la carica assumerà un moto rettilineo uniforme in quanto Ftot=0. Quindi se eE=evB→v=E/B →la particella uscirà dal foro. Variando E e B e possibile discriminare gli e- con una data velocità.

Forza Lorentz sempre ┴ a vel particella (vel parallela a ΔS) , non spinge ne rallenta il movimento, ma ne modifica soltanto la direzione. Poichè la proiezione della forza di Lorentz lungo la direzione della vel è uguale a zero, questa forza non modifica il valore della velocità→W (lavoro)= 0. L’energia cinetica della carica nn cambia.

Moto con velocità perpendicolare a un campo B uniforme:
Se carica q entra in campo magnetico uniforme con una vel ┴ a linee di campo, in tal caso la carica si muove di moto circolare uniforme (xke vel nn cambia). Infatti inoltre B uniforme e ┴ a v, Fq ┴ v e ha modulo qvB costante e sempre contenuta nel piano. Sono queste le caratteristiche della forza centripeta. Quindi per una carica ke si muove in un campo magnetico Fq avrà le proprietà di una forza centripeta e q si muove di moto circolare uniforme.
Quindi Fq= qvB; Fcentripeta=mv2/r →qvB= mv2/r →r=mv/qB

Il flusso del campo magnetico attraverso una superficie piana S:
Фs(B)=B * S     In ogni punto della superficie il vettore Bi ┴ ΔSi quindi la risultante è nulla.

La circuitazione lungo una circonferenza di raggio r ke ha il centro su un filo elettrico ed è posta sul piano perpendicolare a esso coincide con le linee di campo e quindi in ogni punto della curva il campo e la tangente alla curva sono paralleli. La circuitazione non dipende dal raggio della circonferenza: se raddoppiano il raggio  la diminuzione dell’intensità del campo B compensa l’aumento della lunghezza della circonferenza. Se consideriamo due o più fili percorsi da corrente la circuitazione risultante è la somma algebrica delle circuitazioni dei campi prodotti dalle correnti considerate (se verso opposto circuitazione negativa). Quindi secondo il teorema d’ampere la circuitazione di un generico campo magnetico è proporzionale alla somma algebrica delle correnti concatenate.
Cγ(B)= Σi Bi * cosαi * ΔSi      →α=o       →Σ μ0/2п*i/d * 2пr        →d=r           → μ * i
La circuitazione del campo lungo un percorso chiuso ke nn ha alcuna corrente concatenata è nulla. Le linee del campo magnetico sono chiuse su  loro stesse xke in generale la circuitazione di B è diversa da 0. Il campo magnetico a differenza di quello elettrostatico non è quindi conservativo.

 

Fonte: http://styx.altervista.org/Scuola/Fisica/IL_CAMPO_MAGNETICO.doc

 

Autore del testo: non indicato nel documento di origine

 

Campo magnetico

 

 

Visita la nostra pagina principale

 

Campo magnetico

 

Termini d' uso e privacy