Fluidi

 

 

 

Fluidi

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

 

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

 

 

 

Fluidi

 

I FLUIDI

Per fluidi intendiamo i liquidi e gli aeriformi o gas. I liquidi hanno un volume proprio. nel senso che non sono comprimibili, ma assumono la forma del recipiente che li contiene: i gas non hanno ne' volume ne' forma propria. Nella nostro studio ci occuperemo dei liquidi e dei gas che hanno le caratteristiche piu' semplici e che vanno sotto il nome di li­quidi e gas "perfetti".

 

LIQUIDI PERFETTI

 Un liquido si dice perfetto a ideale quando presenta queste due caratteristiche: 1) assenza di viscosíta': quando il liquido si muove, le sue mo­lecole scorrono su piani paralleli e non c'e' nulla che si oppone al movimento del liquido: si dice anche che il liquido non pre­senta attrito interno 2) il liquido e' incomprimibile e indilatabíle: il volume del li­quido non subisce alcuna variazione quando su di esso agiscono delle forze esterne.

 

GAS PERFETTI
Un gas si dice perfetto quando si comporta in base ad una legge  particolare che si chiama legge di Gay‑Lussac e che in formula si esprime come segue
p x V  =  k x T
dove                
k = costante
p = pressione
V = volume
T =  temperatura

La pressione ed ìl volume sono inversamente proporzionali quindi possiamo affermare che un gas perfetto si puo' pensare formato da particelle che non hanno un proprìo volume ma che si comportano come punti materiali che occupano uno spazio quasi nullo
. Esempìo: Aumentando al pressione p che viene esercitata sulla su­perfície del gas contenuto nel recipiente, il volume del gas di­sminuisce

 

 

 

 

Occupiamoci adesso dei liquidi ( perfetti ) e di alcune grandezze fisiche che ci saranno necessarie in seguito.

 

 

 

DENSITA'

La densita' e' definita come la massa divisa per il volume del liquido presa in esame; dì solìto si considera il volume di 1 m o di 1 cm e quindi si parla di "unita' di volume ". In formula si scrive

r = m / V

 

e si misura in Kg/m3  o in gr/cm3 .

PESO SPECIFICO

 Il peso specifico e' definito come la densita' moltiplicata per g (accelerazione di gravita') ossia e' il peso dell'unita' di volu­me della sostanza in esame. In formula si scrive

Ps = ( m  . g )/ V

e si misura in Newton/m3

Molte volte e' necessario conoscere la densita' di una sostanza, e  il suo peso specìfico. in relazione ad un'altra sostanza presa come riferimento. Si parla allora di densita' relativa e di peso specifica relativo. Queste quantita' vanno calcolate rispettiva­mente come rapporto tra la massa di un corpo e la massa di un u­guale volume di una sostanza presa come riferimento a come il rapporto tra il peso di un corpo ed il peso di un uguale volume di una sostanza di riferimento. Sia la densita' relativa che il peso specifico relativo sono espressi come scalari senza l'unita' di misura.

LA PRESSIONE

 Esperimento: introducendo il pistone tra la forza applicata dall'esterno e la superficie del liquido contenuto nel recipiente cilindrico l'effetto della forza non si esercita in un unico pun­to ( come accadrebbe se non ci fosse il pistone ) bensi'  la forza risulta essere distribuita in modo uniforme sull'intera superficie di separazione tra liquido e pistone

 

 

 

La pressione viene definita come il rapporto tra l'intensita' della forza agente e l'area della superficie su cui la forza agisce perpendicolarmente ed in  modo uniforme.
In formula si scrive

 

P = F/S

 e si misura in N/ m2.

 

LA LEGGE DI PASCAL E LE SUE APPLICAZIONI

 

La pressione esercitata ìn un punto della superficie che delimita un fluido si trasmette in tutte le direzioni con la stessa intensità.

Inoltre, in un punto qualsìasi di una superficie che delimita il fluido, la pressione risulterà perpendicolare alla superficie stessa.

 

 

nella figura p    rappresenta la somma della pressione esterna p, e dì quella prodotta dalla colonna di fluido.

                                                

 

Esempio:

Praticando nelle pareti di un recipiente contenente dell'acqua dei fori laterali (quindi in direzione perpendicolare alla forza peso) non vi dovrebbe apparentemente essere alcuna fuoriuscita di liquido.
In realtà l'acqua defluisce dai fori e questo si spiega con la legge di Pascal. Tale fuoriuscita di liquido perdura finchè il suo livello non scenderà al di sotto di quello del foro.
Inoltre, dal foro inferiore sgorgherà uno zampillo più intenso perchè è maggiore la pressione presente in quel punto.

Esempio:

Quando il paziente è costretto ad una lunga degenza a letto, sopravviene il problema delle piaghe da decubíto (cause: attrito, temperatura ecc.).
A ciò si cerca di ovviare con materassini ad acqua o ad aria, distribuendo il peso su di una superficie di appoggio di dimensioni maggiori rispetto ai pochi punti di appoggio che si hanno con un comune materasso‑

Legge di Stevino. Permette di calcolare la pressione nei vari punti di un liquido in quiete. Volendo ad esempio calcolare la pressione agente su un generico punto A di un liquido in quiete, occorre considerare sia l'eventuale pressione esterna sia la pressione esercitata dalla colonna del liquido sovrastante il punto A, detta pressione idrostatica; si ha cioè:

La pressione idrostatica, determinata dalla relazione d.g.h, varia dunque in funzione della densità del liquido, del dislivello dal punto A alla superfìcie libera del liquido, mentre è indipendente dalla forma del recipiente. Inoltre essa agisce in tutte le direzioni con ugual intensità.

 

                         

 

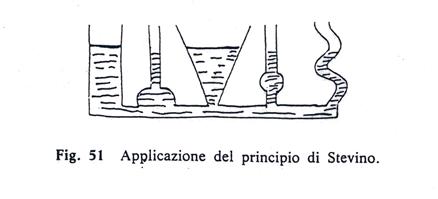
Sembra paradossale, ma la pressione sul fondo di questi recipien-11 di forma diversa, ma riempiti allo stesso livello con lo stesso liquido è sempre la stessa.

 

Esempio:

Un'altro problema che chiama in causa la legge di Stevino riguarda le trasfusioni e le fleboclisi.
Per poter effettuare queste cure si ricorre all’ impiego di piantane (colonne di ferro estensibili) alle quali sono appesi i flaconi.

Il flacone va tenuto più in alto possibile per permettere di aumentare l'altezza della colonna di liquido contenuta nel tubicino di raccordo e quindi la sua pressione.
In questo modo (oltre che variando la sezione del tubo mediante un morsetto) è possibile regolare la velocità di flusso.
Quando il contenuto del fiacone termina, si ha un reflusso di sangue nel tubicino perchè la pressione endovenosa non è più ostacolata da quella dei liquido utilizzato per la flebocfisi.

 

Il barometro di Torricelli

Evangelista Torricelli, circa 400 anni fa, pensò di usare considerazioni analoghe a quelle svolte nel paragrafo precedente per ideare uno strumento atto a misurare la pressione atmosferica.
Egli  fornì una dimostrazione pratica inconfutabile, seguendo un metodo semplice e rigoroso, tanto che il barometro di Torricelli, dal punto di vista dell'affidabilità, è tuttora utilizzato nei laboratori scientifici come standard di riferimento.
La realizzazione di un barometro a mercurio può essere facilmente eseguita, rispettando le seguenti semplici regole: - si prenda un piccolo recipiente e lo si riempia di mercurio, - si prenda poi un tubo di vetro (lungo da 80 cm a 1 m) chiuso ad una estremità e aperto all'altra; - riempito il tubo, tenendone chiusa l'estremità libera, la si immerga nella bacinella senza versarne il contenuto.

 

 

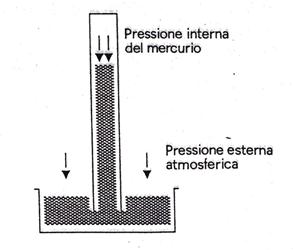
In assenza di pressione atmosferica, il mercurio dovrebbe travasarsi tutto nella bacinella. Ciò invece non accade poiché il suo livello scende inizialmente fino a raggiungere una data altezza, alla quale poi si stabilizza. Questo comportamento è dovuto al fatto che la pressione esercitata dalla colonna di mercurio, col dimunuire dell'altezza di quest'ultima, ha pareggiato la pressione esercitata dall'atmosfera, raggiungendo così una condizione di equilibrio con quest'ultima.

Si può così verificare che la pressione atmosferica, a livello del mare ed in condizioni metereologiche non perturbate, è equivalente alla pressione esercitata da una colonna di mercurio alta 760 mm. Se varia la pressione atmosferica varia di conseguenza l'altezza della colonna di mercurio.
Esempio: 1 mm di Hg = 1 Torr = 133,32 Pa         760 mm di Hg = 1 atm =1013mbar

 

FENOMENI MOLECOLARI NEI LIQUIDI

Nei liquidi si manifestano particolari fenomeni prodotti dalle forze attrattive (forze a corto raggio d'azione, di origine elettrica) che agiscono sulle molecole. Le forze che si esercitano tra molecole di uno stesso liquido vengono definite forze di coesione, mentre le forze di adesione sono quelle che agiscono tra le molecole di un liquido e quelle di un materiale solido. Esempio: Si consideri un recipiente in vetro contenente dell'acqua - le forze di coesione sono quelle che si esercitano tra le molecole di H2O,
- le forze di adesione agiscono tra le molecole di H2O e quelle costituenti le pareti del recipiente.

 

TENSIONE SUPERFICIALE

Questo fenomeno è dovuto a quelle molecole che si trovano in prossimità della superficie di un liquido.
Per queste molecole, contrariamente a quanto succede a quelle che si trovano ad una maggior profondità, la risultante delle forze coesive  (esercitate dalle molecole circostanti) non è nulla, bensì è diretta verso l'interno dei volume dei liquido.

 

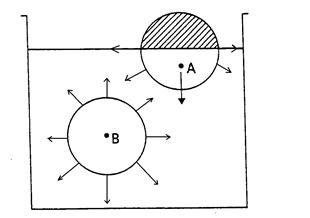
La spiegazione consiste nel fatto che, quando la sfera virtuale (di dimensioni pari al raggio d'azione delle forze coesive) che circonda una generica molecola è completamente riempita di liquido, la forza risultante è nulla per evidenti motivi di simmetria. In caso contrario, la risultante è pari alla somma delle forze esercitate dalle molecole di liquido contenute nell'emisfera inferiore. Pertanto, si manifesta una forza la cui presenza conferisce a tali molecole un'energia potenziale, detta tensione superficiale, che fisicamente ha le dimensioni di una energia diviso una superficie (joule/ m2)

Esempio: Tensioni superficiali di alcuni tra i liquidi più comuni, alla temperatura di 20 °C.

 - Acqua              72,75   mJ/rn2
- Etere                17        mJ/rn2
-  Mercurio         465        mJ/rn2

Le principali conseguenze di questo fenomeno si possono così riassumere:
- occorre un lavoro per vincere l'azione della tensione superficiale,
- tutti i liquidi tendono ad assumere una forma che consenta loro di occupare la superficie minima, ossia quella forma sferica propria delle gocce di liquido,
- le dimensioni delle gocce di liquido sono tanto più piccole quanto maggiore è la tensione superficiale (ossia l'intensità delle forze di coesione).
Esempio:
Il mercurio, che possiede una tensione superficiale notevolmente superiore a quella dell'acqua, si suddivide in gocce di dimensioni minori rispetto a quanto avviene per quest'ultima.
Da un punto di vista pratico si riscontra che sciogliendo un detergente in acqua, se ne provoca una riduzione della tensione superficiale.
La soluzione così ottenuta inumidisce più rapidamente i materiali che vi si immergono e ne consente una più efficace pulizia.

Esempio:
Per il basso valore di tensione superficiale, le soluzioni saponose sono particolarmente indicate per i clisteri.
LA CAPILLARITA'

Se un liquido viene posto all'interno di un recipiente, la curvatura che la sua superficie libera assume in prossimità delle pareti dipende dall'azione esercitata dalie forze coesiva ed adesiva, o meglio, dai rapporto tra le loro intensità.
Mentre l'intensità della forza coesiva costituisce una caratteristica fisica del liquido utilizzato, per quanto riguarda la forza adesiva, essa dipende dalla natura del liquido e del recipiente.
Se infatti le forze adesive risultano più intense di quelle coesive, l'angolo di contatto sarà compreso tra 0° e 90°, ossia  "il liquido bagna le pareti" poiché le sue molecole verranno attratte verso queste ultime. in caso contrario (forze di coesione più intense di quelle di adesione), si dirà che "il liquido non bagna le pareti", poiché l'angolo di contatto sarà compreso tra 90° e 180°.

              

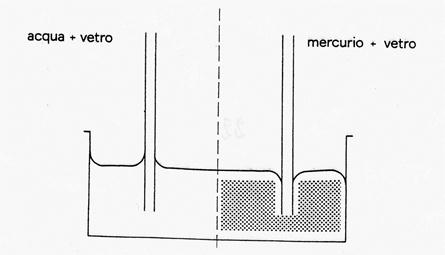
Esempio:
vetro + ioduro di metilene ——»  liquido bagna le pareti
vetro + mercurio          ——>il liquido non bagna le pareti
Uno degli effetti più conosciuti di questo fenomeno è rappresentato dalla capillarità, ossia dall'innalzamento (capillarità positiva) o dall'abbassamento (capillarità negativa) di un liquido all'interno di un tubo aperto di sezione molto piccola (capillare). Sperimentalmente si può osservare che l'innalzamento o l'abbassamento del livello del liquido in un capillare è inversamente proporzionale ai raggio dei tubicino.
Esempio: Alcune comuni manifestazioni del fenomeno della capillarità nella pratica infermieristica sono: - l'azione del cotone idrofilo o delle garze nella fasciatura chirurgica, - il drenaggio chirurgico, - il prelievo di sangue mediante capillare, dopo che si è punto un dito del paziente per ricavarne una goccia.

 

 

La portata è     P  = Area x velocità

Il teorema di Bernoulli

L'applicazione del principio della conservazione dell'energia al moto di un liquido perfetto assume una forma abbastanza semplice infatti, mancando l'attrito non si manifestano scambi di calore con l’esterno e l’unica forma di energia in gioco è quella meccanica.

 

Non intendiamo qui procedere alla dimostrazione della formula che sintetizza la conservazione dell'energia meccanica applicata ai liquidi ideali, ma è già interessante indicarne almeno il punto di partenza.                                              
In riferimento alla figura successiva, quando la porzione di fluido compresa tra le sezioni S1, e S2, avanza, le forze dovute "alla pressione P,, causata dalla presenza del liquido a monte di S1 e quelle dovute alla pressione P, causata dalla presenza del liquido a valle di S1, compiono un lavoro che viene utilizzato per variare 1' energia meccanica del liquido, cioè la sua energia cinetica e la sua energia potenziale gravitazionale.

       

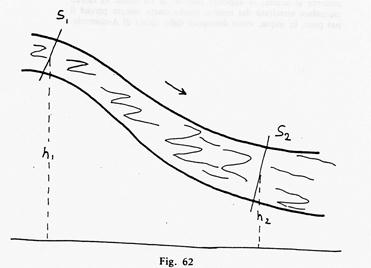
Trascurando i passaggi matematici si arriva al seguente risultato:
Energia totale di un fluido è data da :
Pressione + Energia Cinetica + Energia Potenziale

Il contenuto veramente importante del teorema di Bernoulli e cioè che l'energia meccanica posseduta da un liquido ideale in moto è suddivisa in tre  forme: energia di pressione, energia cinetica ed energia potenziale gravitazionale. Durante il movimento del liquido l’energia può trasformarsi da una forma all'altra sempre però con reciproche compensazioni in modo che la quantità totale di energia rimanga sempre costante.
Il teorema di Bernoulli può venire utilizzato per dimostrare che in corrispondenza di una strozzatura di un condotto la pressione diminuisce.

 

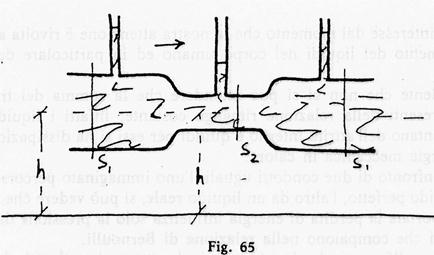
Tenendo ora presente che la portata è costante si sa che la velocità è maggiore là dove la sezione è minore; affinchè valga dunque l'uguaglianza, la pressione deve essere minore proprio in corrispondenza della sezione più piccola, contrariamente a quanto si potrebbe intuitivamente pensare.
I vasi sanguigni subiscono spesso variazioni della loro sezione a causa contrazione dei muscoli che li circondano, ma essendo le loro pareti elastiche, essi sono normalmente in grado di sopportare le conseguenti variazioni di pressione.
Può però succedere in vasi malati o vecchi, le cui pareti hanno perso la normale elasticità e quindi la capacità di reazione, che ad un accidentale aumento della sezione corrisponda un aumento della pressione che procura a sua volta una ulteriore dilatazione della sezione fino ad una eventuale rottura; e viceversa che una accidentale diminuzione della sezione provochi una diminuzione della pressione che a sua volta favorisce una ulteriore diminuzione della sezione fino all'occlusione del vaso. In ogni caso si hanno dannose conseguenze per l'intero organismo.
Ulteriori informazioni sul comportamento dei liquidi reali si ricavano volendo adattare ad essi il teorema di Bernoulli; l'argomento è di grande interesse dal momento che la nostra attenzione è rivolta al comportamento dei liquidi nel corpo umano ed in particolare del sangue.

È evidente che non ci si può attendere che la somma dei tré termini presenti nella relazione rimanga costante; infatti i liquidi reali presentano dell'attrito interno e quindi per essi si ha dissipazione di energia meccanica in calore.

Nel confronto di due condotti uguali, l'uno immaginato percorso da un liquido perfetto, l'altro da un liquido reale, si può vedere che a parità di portata la perdita di energia influenza solo la pressione dei tré termini che compaiono nella relazione di Bernoulli.
Infatti, nell'ipotesi che la portata sia la stessa, la velocità del liquido dipende solo dalla sezione e la quota è solo un parametro geometrico; di conseguenza la dissipazione di energia meccanica in calore può riflettersi solo in una perdita di pressione.

 

 

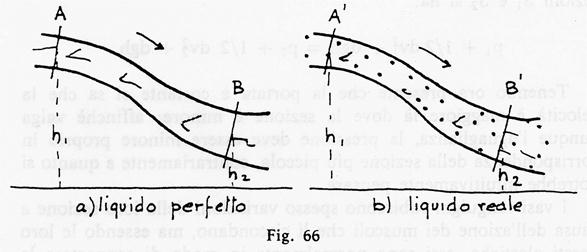
Nel caso del liquido perfetto se l'energia specifica totale vale ad esemplo 100 a livello della sezione A, vale ancora 100 a livello della sezione B.
Per il liquido reale invece se l'energia specifica totale vale 100 a livello della sezione A, a causa della dissipazione in calore per gli attriti, vale 80 a livello della sezione B.
Si può quindi scrivere:
Pressione + En. Cinetica + En. Potenz     =  100 per il liquido perfetto nel punto B
Pressione + En. Cinetica + En. Potenz     =   80 per il liquido reale nel punto B
Ma Velocità B = Velocità B’ (essendo le sezioni uguali ed avendo supposto la  portata uguale); h B= hB’  (per l'ipotesi fatta della stessa geometria dei due condotti), e perciò p B   deve essere minore di p B’  

Si può concludere che gli attriti interni sono responsabili della caduta di pressione lungo il condotto; si dice usualmente che si ha una perdita di carico.     
A maggior chiarimento di quanto fìnòra detto, consideriamo il caso più semplice, cioè quello di un condotto orizzontale a sezione costante.
Se esso è percorso da un liquido ideale la pressione rimane costante qualunque sia la sezione che si prende in considerazione, essendo sempre costanti gli altri termini.

 

                              

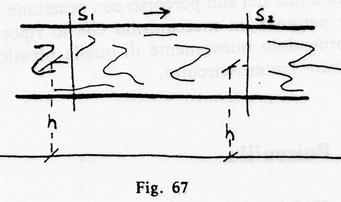
da cui P1 == P1.

 

Questa situazione è paragonabile al moto rettilineo uniforme di un corpo su un piano senza attrito, in assenza di una forza risultante. Se il condotto precedente fosse invece percorso da un liquido reale si registrerebbe una diminuzione di pressione nella dirczione del moto:

 

                                 

 

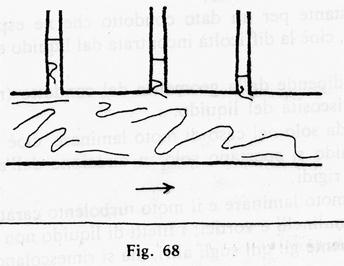
Il moto di un liquido può quindi essere mantenuto da una differenza di pressione capace di compiere il lavoro che si perde per gli attriti sottoforma di calore.
Queste considerazioni dovrebbero aiutare a capire la necessità di introdurre una pompa ( il cuore) nel caso della circolazione del sangue, che avviene in un circuito chiuso.
Il sangue giunge alla fine del suo percorso con pressione praticamente nulla; occorre pertanto  un meccanismo che lo riporti nella situazione iniziale, fornendo nuovamente quella pressione che gli serve per ripercorrere l’intero circuito.

 

fonte: http://filer.amm.unibs.it/content/dav/unibs/med/edoardo.selva/Pub/Fisica/Fluidi1.doc

Autore del testo: non indicato nel documento di origine

 

Fluidi

 

 

Visita la nostra pagina principale

 

Fluidi

 

Termini d' uso e privacy