Leggi di Keplero sintesi e spiegazione
Leggi di Keplero sintesi e spiegazione
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
LE LEGGI DI KEPLERO
LE LEGGI DI KEPLERO
Il modello geocentrico ideato da Tolomeo, che prevedeva un complesso sistema “ad orologeria” formato da 55 sfere in movimento e che avevano come centro la terra, cominciò a crollare con Niccolò Copernico , il quale , venuto a conoscenza delle idee di Aristarco di Samo (310-250 a.C.) , provò a collocare il Sole al centro del sistema con tutti i pianeti in rotazione attorno ad esso.
Spiegò in questo modo i moti retrogradi dei pianeti e la variazione della loro distanza dalla Terra. Tuttavia non aveva prove a suo favore e il suo modello non spiegava i moti dei pianeti con maggiore precisione del modello geocentrico.
Solo l’opera di grandi scienziati come Keplero , Galileo e Newton renderà questo modello aderente alla realtà e lo farà accettare universalmente.
Johannes Kepler o Giovanni Keplero ( Weil der Stadt , 27 dicembre 1571-Regensburg, 15 novembre 1630) fu un astronomo e un matematico tedesco. Keplero ereditò da Tycho Brahe una gran quantità dei più precisi dati mai raccolti sulle posizioni dei pianeti. Il problema era dare loro un senso. I movimenti orbitali e gli altri pianeti sono visti dal punto vantaggioso della Terra, che orbita a sua volta intorno al Sole.

Questo fa si che i pianeti sembrino muoversi disegnando strane curve. Keplero volle concentrarsi sull’orbita di Marte, anche se prima avrebbe dovuto studiare accuratamente l’orbita della Terra. Per far questo, usò come linea di base il Sole e una delle due intersezioni dell’orbita di Marte con il piano dell’ellittica. Questo pianeta era particolarmente adatto allo scopo proprio perché la sua orbita ha la massima inclinazione con tale piano . Usando tale base poté calcolare le posizioni della Terra e ricavare poi l’intera orbita di Marte. Egli fu inoltre capace di dedurre le sue leggi sui pianeti senza conoscere l’esatta distanza dei pianeti dal Sole, poiché le sue analisi geometriche richiedevano solo il rapporto tra le rispettive distanze dal Sole.
Alla fine giunse a formulare le sue tre leggi sui movimenti planetari che enunciò nelle tavole rudolfine, così chiamate in onore di Rodolfo II . In tali tavole introdusse anche i logaritmi neperiani per agevolare i calcoli astronomici.
Le prime due leggi furono pubblicate nel 1609 mentre la terza fu pubblicata nel 1619.
Si tratta però di leggi puramente descrittive. Sono leggi che permettono di prevedere con buona approssimazione le posizioni future dei pianeti. Ma non spiegano perchè il moto sia proprio quello. Sarà Isaac Newton che riuscirà in seguito a dare risposta al problema delle forze che sono responsabili dei moti dei corpi celesti, descritti dalle tre leggi di Keplero, unificando i principi della meccanica celeste e quelli della meccanica terrestre.
PRIMA LEGGE DI KEPLERO
- I pianeti descrivono orbite ellittiche, quasi complanari, aventi tutte un fuoco comune in cui si trova il Sole.
Il senso della rivoluzione intorno al Sole è in genere antiorario.

Nella figura è rappresentata un orbita ellittica, con indicati i suoi parametri caratteristici:
- Il punto dell’orbita più vicino al Sole è chiamato perielio e corrisponde al punto A. Viceversa il punto più lontano è chiamato afelio e corrisponde al punto B.
- La distanza tra il punto A e il centro dell’ellisse (punto C) viene chiamata semiasse maggiore dell’orbita. Ovviamente la distanza tra il punto B e il punto C è la stessa.
- La distanza tra il punto D e il centro dell’ellisse viene chiamata semiasse minore dell’orbita.
- La distanza fra il Sole e il centro dell’ellisse viene chiamata semi-distanza focale. Viene indicata con la formula:

- L’eccentricità dell’orbita è la differenza tra la distanza Sole-afelio e la distanza Sole-perielio.
SECONDA LEGGE DI KEPLERO
Keplero propose la seguente regola per prevedere l’aumento o la diminuzione della velocità. Tracciamo una linea (“raggio vettore”) dal centro del Sole al pianeta. La legge di Keplero afferma:
- Il raggio vettore descrive superfici con aree uguali in intervalli di tempo uguali.
Se l’orbita è allungata, cioè l’eccentricità è grande, il pianeta, allontanandosi dal corpo intorno a cui ruota, rallenta, mentre , riavvicinandosi ad esso, riprende di nuovo
velocità. Il pianeta si muove quindi più rapidamente quando si trova nel punto più vicino, perielio, mentre si muove più lentamente quando si trova nel punto più lontano, afelio. A spiegare il perché la velocità dei pianeti vari a secondo della vicinanza o lontananza dal Sole sarà Newton, il quale affermerà che il Sole,avendo una massa maggiore rispetto agli altri pianeti, esercita un forza gravitazionale molto grande, tale che i pianeti, per non essere risucchiati da questa, cominciano a girare più velocemente.
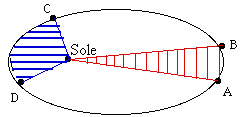
Supponiamo che il disegno sopra rappresenti l’orbita di un pianeta che ruota intorno al Sole, e siano AB e CD due tratti di orbita percorsi in 3 ore vicino all’afelio e vicino al perielio,rispettivamente. Se indichiamo con O il centro del Sole, le aree tratteggiate OAB e OCD sono uguali. Questo significa ovviamente che CD è molto più lungo di AB, poiché vicino al perielio il pianeta si muove molto più rapidamente e percorre una distanza molto maggiore nelle stesse 3 ore.
TERZA LEGGE DI KEPLERO
- I quadrati dei periodi di rivoluzione (tempi che i pianeti impiegano a percorrere le loro orbite) sono proporzionali ai cubi delle loro distanze medie dal Sole.
In altre parole, la velocità media di un pianeta è tanto minore quanto più esso è lontano dal Sole. Questa legge è valida anche per i satelliti che orbitano intorno ai pianeti e può essere espressa in forma matematica nel modo seguente:
K = T2 / d3
Dove K è una costante ( qualche volta detta di Keplero) , che dipende dal corpo celeste preso in considerazione.
Per un orbita circolare la si riduce a:
 Dove r è il raggio dell’orbita.
Dove r è il raggio dell’orbita.
LIMITI DELLA VALIDITA’ DELLE LEGGI DI KEPLERO
Va specificato che le leggi di Keplero sono precise nella misura in cui sono soddisfatte le seguenti ipotesi:
- La massa del pianeta è trascurabile rispetto a quella del Sole;
- Si possono trascurare le intersezioni tra i diversi pianeti ( tali intersezioni portano a leggere perturbazioni sulla forma delle orbite).
Fonte: http://www.francescozumbo.it/zumbo/lavori-studenti/2008/cd-5g-2007-2008/lavori/ianno%20maria%20federica.doc
Autore: IANNO’ MARIA FEDERICA
Leggi di Keplero sintesi e spiegazione
I pianeti:

Intorno al Sole si muovono i pianeti, corpi celesti relativamente freddi che riflettono la luce che ricevono dal Sole. Essi sono nove e hanno tutti una forma quasi sferica. Il moto di un pianeta su se stesso è detto rotazione; il moto intorno al Sole rivoluzione. Il tempo di rotazione di un pianeta è chiamato giorno; il tempo di rivoluzione anno. Il moto di rivoluzione dei pianeti è descritto dalle tre leggi di Keplero:
- La prima legge riguarda la forma dell’orbita : i pianeti percorrono intorno al Sole un’orbita ellittica, in cui il Sole occupa uno dei due fuochi. Il punto dell’orbita più vicino al Sole è detto perielio, il punto più distante afelio. La linea che congiunge perielio e afelio è l’asse maggiore dell’ellisse e viene chiamata linea degli apsidi.
- La seconda legge riguarda la velocità: ogni pianeta si muove sulla sua orbita in modo tale che la linea che lo congiunge al Sole spazza aree uguali in tempi uguali. Ma tale velocità varia di giorno in giorno: la velocità massima si ha quando il pianeta è in afelio, la velocità minima quando è in perielio.
- La terza legge mette in relazione la distanza di un pianeta dal Sole con il tempo necessario a percorrere l’intera orbita: il rapporto tra il quadrato dei tempi di rivoluzione dei pianeti e il cubo della loro distanza media dal Sole è costante.
Le tre leggi di Keplero descrivono, ma non spiegano, i movimenti dei pianeti. La spiegazione di questi movimenti è da cercare nella legge di gravitazione universale, formulata da Isaac Newton. Egli scoprì che due corpi aventi rispettivamente massa m e m¹ si attraggono con una forza, F, direttamente proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della loro distanza, d:

dove G è la costante di gravitazione universale.
In base alla posizione rispetto al Sole e alla diversa costituzione chimica e fisica si distinguono:
- Pianeti di tipo terrestre o interni, Mercurio, Venere, Terra, Marte: hanno piccola massa, bassa velocità di rotazione, nessuno o pochi satelliti; sono rocciosi e costituiti da elementi pesanti, hanno perciò una densità elevata.
- Pianeti di tipo gioviano o esterni, Giove, Saturno, Urano, Nettuno: hanno grande massa, alta velocità di rotazione, sono costituiti da ghiaccio e gas leggeri, mancano di una superficie solida e hanno bassa densità; hanno un numero elevato di satelliti.
- L’ultimo pianeta noto del Sistema Solare è Plutone, che sembra avere caratteristiche in parte simile ai pianeti interni e in parte simili ai pianeti esterni.
Oltre ai pianeti e ai loro satelliti nel Sistema Solare ci sono anche corpi minori: asteroidi, comete, meteore e meteoriti.
Fonte: http://skuola.tiscali.it/sezioni/tesine/tesina-leggerezza-pesantezza.doc
Autore: Scialpi Caterina
Le leggi di Keplero e la Gravitazione Universale
La prima ed importante verifica della validità del Sistema copernicano, venne da Keplero che poté utilizzare osservazioni di Marte molto accurate fatte dal suo maestro Tycho Brahe (1546-1601). Dopo vari tentativi e dieci anni di lavoro, Keplero pervenne in modo empirico alla formulazione delle tre leggi che portano il suo nome:
Ia Legge di Keplero: I pianeti descrivono intorno al Sole delle orbite ellittiche, di cui il Sole occupa uno dei fuochi.
Con questa legge cade il principio della circolarità dei moti planetari. Inoltre le orbite descritte dai pianeti acquistano identità fisica rispetto alle circonferenze tolemaiche, enti puramente geometrici.
IIa Legge di Keplero: Le aree descritte dal raggio vettore di ciascun pianeta sono proporzionali ai tempi impiegati a descriverle; ossia, il raggio vettore di un pianeta descrive aree uguali in tempi uguali.
Come conseguenza di questa legge, un pianeta si muove più velocemente quando è più vicino al Sole (perielio) e più lentamente quando è più lontano (afelio). Questa legge segna la caduta del principio dell’uniformità dei moti planetari.
IIIa Legge di Keplero: I quadrati dei tempi di rivoluzione dei pianeti intorno al Sole sono proporzionali ai cubi dei semiassi maggiori delle rispettive orbite.
Ne segue che la velocità media di un pianeta sulla propria orbita è tanto minore quanto più esso è lontano dal Sole.

Figura 4.
Le leggi di Keplero descrivono compiutamente il moto dei pianeti, ma non ne risalgono alle cause. Perché i pianeti circolano intorno al Sole, anziché allontanarsene in linea retta? Perché un corpo qualsiasi lasciato cadere precipita al suolo mentre questo non accade ai pianeti (Terra compresa) che non precipitano sul Sole?
I gravi in caduta libera con moto accelerato, ma pure i pianeti costretti a muoversi intorno al Sole e la Luna intorno alla Terra, provano l'esistenza di forze centrali che deviano i corpi materiali dalla condizione di moto rettilineo uniforme. Nel 1684 Newton fu in grado di enunciare la Legge di Gravitazione Universale:
due punti materiali qualsiasi si attraggono lungo la loro congiungente con una forza direttamente proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della distanza.
In formula, dette m1 ed m2 le masse dei due corpi, d la loro distanza ed F la forza agente, si ha: F = G(m1m2)/d2, dove G è la costante di Gravitazione (6.67·10-11N m2 /Kg2)
La Legge di Gravitazione è stata definita "Universale" in quanto la forza che regola la caduta dei gravi sulla Terra ed il moto dei pianeti nel cielo è la stessa. I cieli non sono più imperturbati e regolati da leggi divine, ma soggiacciono alle stesse leggi che regolano i fenomeni terrestri. Con l'opera di Newton (i cui risultati furono pubblicati nel 1687 nei Philosophiae Naturalis Principia Mathematica) alla visione del mondo che salva la realtà metafisica, si sostituisce una visione del mondo che descrive la realtà attraverso leggi fisiche, di valore universale, che hanno come banco di prova l'esperimento. La Storia ci dice che questo passaggio non fu indolore.
Fonte: http://www.science.unitn.it/~fisica1/fisica1/appunti/mecc/appunti/gravitazione/gravita_bedogni.doc
Autore del testo: Roberto Bedogni
Leggi di Keplero sintesi e spiegazione
Visita la nostra pagina principale
Leggi di Keplero sintesi e spiegazione
Termini d' uso e privacy