Termodinamica

 

 

 

Termodinamica

 

I riassunti, le citazioni e i testi contenuti in questa pagina sono utilizzati per sole finalità illustrative didattiche e scientifiche e vengono forniti gratuitamente agli utenti.

 

Appunti di termodinamica con grafici

 

Che cos’è la termodinamica ?

 

La termodinamica studia e analizza un sistema dal punto di vista degli scambi di calore e lavoro.
Per fare questo, la termodinamica fonda le sue radici su due principi fondamentali, grazie ai quali possiamo studiare e prevedere le reazioni di motori termici o addirittura di corpi celesti, dell’atmosfera terrestre o del corpo umano.
In generale il primo principio della termodinamica analizza la differenza dell’energia interna considerando non solo il lavoro ma anche il calore; il secondo pone dei limiti alla trasformazione del calore in lavoro, condizioni applicabili alle macchine reali, ma che purtroppo non sono troppo prese in considerazione dalla società consumistica in cui viviamo.

 

Se prendiamo in esame un cilindro perfettamente isolato dall’ambiente esterno, che abbia altresì la base come un perfetto conduttore di calore, possiamo, nel caso di un fluido omogeneo o un gas perfetto, studiare gli scambi di calore e lavoro tramite delle misure quali la pressione, il volume e la temperatura(le così dette variabili termodinamiche), che verranno misurate tramite degli appositi strumenti(manometro, una scala graduata e un termometro).
Nel caso del volume ovviamente, essendo a conoscenza dell’area di base del cilindro, basterà moltiplicarla per l’altezza del pistone che la scala graduata andrà a misurare.
Nel caso in cui fossimo a conoscenza di alcune delle sue misure(pressione e volume; pressione e temperatura; volume e temperatura), e del numero di moli (n), potremmo facilmente risalire alla misura restante tramite l’equazione:

 

                 pV=nRT

dove R è un numero noto (8,315), p è la pressione (pascal), V il volume(metri cubi), T la temperatura(°C) e n appunto il numero di moli.
L’equazione sopraindicata è una così detta “equazione di stato”, e tramite questa possiamo definire gli stadi intermedi di una trasformazione, che nel grafico vengono rappresentati con un punto.

 

In base al movimento del pistone, abbiamo un primo stato dove il volume ha un certo valore, così come la pressione, e un secondo stato, nel quale i valori del volume e della pressione sono cambiati.

 

 

 

 

Le trasformazioni termodinamiche

 

Analizzando le trasformazioni sui gas perfetti possiamo evidenziarne tre tipi fondamentali:

• Trasformazioni isobare

Le trasformazioni isobare sono le trasformazioni che avvengono a pressione costante, e vengono rappresentate sul grafico pressione-volume, con un segmento parallelo all’asse delle ascisse

 

 

 

 

 

 

 

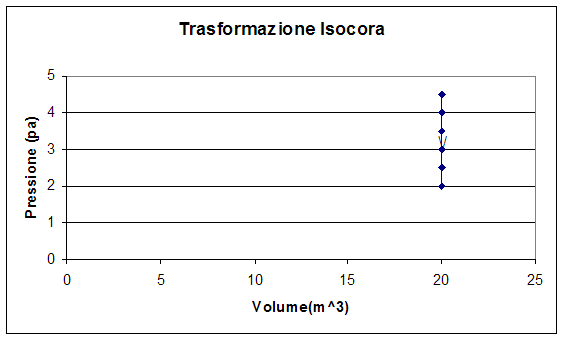
• Trasformazioni isocore

Le trasformazioni isocore sono le trasformazioni che avvengono a volume sostante, e vengono rappresentate sul grafico pressione-volume, con un segmento parallelo all’asse delle ordinate

 

 

 

 

 

 

 

 

 

• Trasformazioni isoterme

Le trasformazioni isoterme sono le trasformazioni che avvengono a temperatura costante, e vengono rappresentate sul grafico pressione-volume, con un arco di iperbole equilatera

 

 

 

 

Abbiamo poi altri due tipi di trasformazioni:

• Trasformazioni adiabatiche

Le trasformazioni adiabatiche sono le trasformazioni che avvengono in assenza di scambi di calore tra il sistema e l’ambiente esterno.

 

 

 

 

• Trasformazioni cicliche

Le trasformazioni cicliche sono le trasformazioni nelle quali lo stato iniziale della trasformazione coincide con lo stato finale. Di conseguenza la differenza di energia interna è nulla.

Le Trasformazioni Quasistatiche

Prendendo in considerazione il cilindro precedentemente analizzato, possiamo trarre delle significative conclusioni.

Immaginiamo di spostare di colpo il pistone verso l’alto:
una serie di trasformazioni interne all’ambiente del cilindro, ostacola che la pressione ed il volume possano rimanere costanti.
Inoltre, nel momento in cui il gas viene a contatto con il pistone, torna indietro come se vi rimbalzasse contro.
Dopo un numero indeterminato di volte che questo “ciclo” si ripete, lo stato del gas all’interno del cilindro è variato.

Se questa rapida trasformazione tra uno stato A ed uno stato B venisse rappresentata in un grafico, questo non sarebbe certamente una retta, bensì avrebbe forma di fuso, in quanto, prima di arrivare allo stato B, ben definito, passa attraverso una serie di innumerevoli stadi intermedi, per poi stabilizzarsi.

 

Ci sono delle trasformazioni che sono dette quasistatiche.
Queste si ottengono spostando l’ipotetico pistone verso l’alto, ma in modo infinitamente più lento di quanto non abbiamo fatto in precedenza.
Così notiamo nel grafico che quello che in precedenza veniva a delinearsi come un unico grande fuso da uno stato A ad uno stato B, ora si è “trasformato” in una serie di fusi molto più piccoli, ma che formano quasi un arco di curva.
In questo caso la trasformazione è detta quasistatica.

 

Il lavoro in un sistema termodinamico

 

Nel momento in cui abbiamo una variazione di volume, s’è un conseguente lavoro: del sistema, nel caso in cui il volume all’interno del cilindro sia aumentato, e quindi il pistone si sia alzato (espansione); dall’esterno, nel momento in cui il volume all’interno del cilindro diminuisce, conseguentemente all’abbassamento del pistone ( compressione).

In una trasformazione isobara

Come detto in precedenza, con trasformazione isobara si intende una trasformazione a pressione costante, quindi, la pressione esercitata dal gas sul pistone, e quella esercitata dal pistone sul gas, si eguagliano.

Allora il lavoro è dato da:

W = Fh = pSh

Dove pS è un derivato della formula della pressione ( p = F/S ), e h è l’altezza del pistone. Notiamo allora che il prodotto S*h, non è altro che la variazione di volume, quindi il lavoro sarà uguale a:

W = p∆V
Più in generale comunque, esiste un metodo per calcolare il lavoro in una trasformazione quasistatica qualunque: basta calcolare l’area della figura che viene a delinearsi, che ha come basa la variazione del volume ( ∆V ), e come altezza la pressione ( p ).

In una trasformazione ciclica

Lo stesso discorso vale per una trasformazione ciclica: se consideriamo il percorso dallo stato A allo stato B come un lavoro positivo, e poidallo stato B allo stato A come un lavoro negativo, giungiamo ala conclusione che il lavoro è uguale alla somma algebrica del lavoro speso nei due cambiamenti di stato:

Wtc = W a-b +  Wb-a

Ma, considerato che come abbiamo detto prima si tratta della somma algebrica del lavoro positivo iniziale, meno quella del lavoro negativo della seconda fase, in definitiva il lavoro sarà uguale all’area della parte di piano racchiusa dalla trasformazione ciclica.

Da quanto abbiamo detto finora possiamo dedurre che il lavoro non è una funzione di stato, in quanto non dipende solo dai valori di un ipotetico stato A e un altro ipotetico stato B, bensì anche dal particolare tipo di trasformazione a cui il sistema è sottoposto.

 

Il primo principio della termodinamica

Potendo essere considerato come un’estensione della legge di conservazione dell’energia meccanica, il primo principio della termodinamica tiene in considerazione gli scambi di calore tra il sistema e l’esterno, e viceversa, oltre che il lavoro.

 

 

La variazione dell’energia interna varia a seconda degli scambi di calore e del lavoro esercitato sul sistema dall’esterno e viceversa.

Quindi la somma algebrica di tutti gli scambi di calore più la somma algebrica di tutto il lavoro compiuto ha come risultato la variazione di energia interna:

∆Utot = Qtot + W(e)tot

 
Nel caso in cui il lavoro sia compiuto dal sistema, poiché è esattamente opposto, la formula ha una piccola variazione:

∆Utot = Qtot - Wtot

 

 

Trasformazioni isocore

Come già esposto in precedenza, una trasformazione isocora si ottiene mantenendo costante la misura del volume.
In questo caso il lavoro sarà uguale a zero (è facile notarlo anche per l’impossibilità di calcolare un’area, la quale indica il lavoro, per l’assenza di un ∆V ad indicare una base):

W = ∆Vp = 0

Ne consegue che, per l’assenza del lavoro, basandoci sulla formula precedente, la variazione di energia interna è uguale al calore speso:

∆U = Q

Trasformazioni isobare

Le trasformazioni isobare, sono le trasformazioni che avvengono a pressione costante. In questo caso il sistema compie lavoro sull’ambiente:

p∆V + ∆U = Q

 

Considerando però che in una trasformazione isobara il lavoro che si ottiene è circa un sesto del calore prodotto, possiamo capire come nella trasformazione isocora, l’aumento di temperatura, e la conseguente variazione di energia interna, sia maggiore che in una trasformazione isobara.

 

Trasformazioni adiabatiche

Le trasformazioni adiabatiche sono le trasformazioni che avvengono senza scambio di calore alcuno; come se avvenissero all’interno di un cilindro perfettamente isolato dall’esterno.
Quindi, poiché gli scambi di calore risultano nulli, arriviamo alla conclusione che:

∆U = -W

Durante una trasformazione adiabatica, ovviamente, la temperatura diminuisce se diminuiamo il valore della pressione su un ipotetico pistone, ed aumenta nel caso in cui aumentiamo il valore della pressione, generando così un lavoro negativo da parte del sistema.

 

Trasformazioni cicliche

Nel caso delle trasformazioni cicliche, il valore della variazione dell’energia interna, essendo questa un’equazione di stato, ed essendo lo stato iniziale e quello finale identici, è uguale a zero:

∆U = 0

Possiamo così dedurre che la quantità di calore scambiato è uguale al lavoro compiuto:

Qtot = Wtot

 

 

La macchina a vapore

La “Macchina vapore” è composta da quattro differenti macchine. Ogni macchina costituisce un singolo sistema aperto del quale possiamo calcolare e studiare il bilancio energetico. La somma di questi quattro sistemi aperti genera un unico sistema.

 

 

La figura mostra un diagramma schematico di un impianto elementare a vapore per la produzione di energia. I cicli a vapore costituiscono un esempio importante per la produzione di energia elettrica, specialmente usata negli impianti a larga scala per l’inconveniente derivato dal fatto che questi impianti necessitano di ampi spazi. Il funzionamento di questo impianto si basa su continue variazioni di pressioni e volume di una relativamente piccola massa costante di acqua che viene fatta passare, tramite una pompa, attraverso la caldaia, successivamente nella camera di espansione e poi nel condensatore. Generalmente il liquido usato è l’acqua (demineralizzata per evitare le incrostazione di calcare), date le favorevoli proprietà termodinamiche, il basso costo e la grande disponibilità, ma non mancano applicazioni particolari nelle quali vengono impiegati altri fluidi.

 

Il funzionamento della macchina a vapore è fondamentalmente di tipo ciclico, e si basa sull’esistenza di almeno due sorgenti di calore,.
Il calore passa dalla sorgente più alta, e fa in modo che il vapore spinga un ipotetico pistone, compiendo così un lavoro verso l’esterno.
Arrivato ad un certo punto però il pistone deve ritornare al punto di partenza;allora la seconda sorgente ( un condensatore ), raffredda il fluido contenuto nel sistema, facendo in modo che il vapore ritorni allo stato liquido, e che il pistone torni al punto di partenza.
Come sappiamo il lavoro che si compie è di gran lunga minore del calore che si crea, il quale viene in un certo senso “sprecato” per raffreddare il fluido, tramite il condensatore.

 

Il secondo principio della termodinamica

E’ arrivato il momento di porsi un quesito:
Siamo sicuri che è possibile trasformare un’intera quantità di lavoro in calore; ma è possibile trasformare un’intera quantità di calore in lavoro ?

Se esistesse una macchina capace di trasformare un’intera quantità di calore in lavoro, basterebbe il raffreddamento di 1K dell’acqua del mare, per generare una notevolissima quantità di energia.
Così facendo potremmo risolvere i nostri problemi energetici per migliaia e migliaia di anni.
Ma purtroppo una macchina del genere non esiste, come è anche testimoniato dagli enunciati di Lord Kelvin e di Clausius.

 

L’enunciato di Lord Kelvin

“E’ impossibile realizzare una trasformazione il cui unico risultato sia quello di assorbire una determinata quantità di calore da un’unica sorgente di calore e trasformarla integralmente in lavoro”.

Quanto appena detto potrebbe sembrare in contraddizione con quanto visto in precedenza. Infatti in una trasformazione isoterma, tutto il calore assorbito dalla sorgente è trasformato in lavoro. Ma il pistone si trova in una posizione differente da quella iniziale.
Quindi affinché il pistone torni alla sua posizione, il sistema deve scambiare calore con l’esterno. Questo avviene ad una temperatura differente da quella della prima isoterma, quindi vi sono almeno due sorgenti di calore.
Capiamo così come le parole evidenziate siano fondamentali per non fraintendere l’enunciato.

 

L’ enunciato di Clausius

“E’ impossibile realizzare una trasformazione il cui unico risultato sia quello di far passare calore da un corpo più freddo ad uno più caldo”.

Anche qui è necessario pesare le parole.
Infatti, un frigorifero per esempio, preleva calore da una sorgente fredda, e la riversa nell’ambiente. Ma questo avviene in presenza di lavoro, quindi non è in contraddizione con l’enunciato di Clausius.

Questi due enunciati sono in un certo senso complementari.

Infatti possiamo dimostrarli entrambi per assurdo, servendoci anche di uno dei due enunciati che non prendiamo subito in questione. Per esempio:

Se prendiamo in considerazione una sorta di macchina “anti-Clausius”, capace appunto di far passare calore da un corpo più freddo ad uno più caldo, e la uniamo ad una macchina con due sorgenti di calore, osserviamo che:

 

• la sorgente a temperatura più alta, cede un calore “Q2”, il quale serve a far compiere un lavoro alla macchina, e del quale buona parte, come già detto in precedenza, viene “sprecato”, e ceduto alla sorgente a temperatura minore.
• E’ qui che entra in gioco la macchina “anti-Clausius”:

 la quantità di calore ceduta alla sorgente più fredda, viene ceduta          nuovamente alla sorgente iniziale.

A conti fatti, abbiamo analizzato una macchina che ha una sola sorgente di calore. Questo è in contraddizione con l’enunciato di Lord Kelvin. 

Possiamo ora fare lo stesso con una macchina “anti-Klausius”:

Nel caso in cui per esempio il fine della suddetta macchina sia quello di alzare i pesetti di una macchina di Joule, con all’interno acqua ad una temperatura T’>T, al termine del lavoro, la variazione di energia interna sarà uguale a tutto il lavoro compiuto sul mulinello di Joule, che sarebbe pari alla variazione di temperatura.
Assisteremmo così al passaggio di calore da una sorgente “T”, più fredda, ad una “T’”, più calda, senza alcun tipo di lavoro. Questo è in contraddizione con l’enunciato di Clausius.

E’ ora necessario introdurre il concetto di trasformazione reversibile e di rendimento:

• come è facile intuire, una trasformazione cosiddetta reversibile, è una trasformazione grazie alla quale, passando da uno stato “A” ad uno stato “B”, è possibile tornare ad uno stato “A”, ripercorrendo esattamente a ritroso il percorso per arrivare allo stato “B”, e avendo nel punto “A”, esattamente le stesse condizioni iniziali.

 

• Quando avviene una trasformazione, non tutto il calore viene trasformato in lavoro, ma solo un’esigua percentuale.

Il rendimento di una macchina termica è uguale al rapporto tra il lavoro totale ed il calore ceduto dalla sorgente più calda:

η = Wtot
Q2

Per una macchina termica che deve necessariamente lavorare con almeno due sorgenti di calore, poiché il lavoro totale è uguale a Q2 – │Q1│, deduciamo che:

η = Q2 – ׀Q1= 1- ׀Q1׀
          Q2            Q2

 

Tra le macchine reversibili, tra le più importanti annoveriamo le macchine reversibili di tipo termico.
Su questo tipo di macchine vi è un teorema importante, conseguito da Sadi Nicolas Lèonard Carot, il quale asserisce che le macchine reversibili hanno un rendimento maggiore a quelle non reversibili, se ovviamente entrambe lavorano tra due stesse temperature.

Possiamo a questo punto dimostrare il cosiddetto Teorema di Carnot :

ηR= 1 – ׀Q1 R ׀  
Q2R

Dove R sta ad indicare che stiamo analizzando una macchina di tipo reversibile. Ora passiamo ad una macchina non reversibile, che rappresenteremo con la lettera S:
ηS= 1 – ׀Q1 S ׀  
Q2S

 

È utile inoltre osservare che:

WRtot = QR2 – │QR1│  e   WStot = QS2 – │QS1│

Volendo dunque dimostrare per assurdo il teorema di Carnot, procederemo come segue:

ηR < ηS

sostituendo quindi le formule precedentemente ottenute, otteniamo:

1 – ׀Q1 R   <  1 – ׀Q1 S ׀  
Q2R                       Q2S

E dopo le opportune operazioni:

׀Q1 R    >   ׀Q1 S ׀  
Q2R                Q2S

Se poi invece poniamo QR2 = QS2 otteniamo:

│QR1│  – │QS1 │> 0

abbiamo preventivamente eliminato i denominatori, perché in questo caso sono uguali. Considerato che stiamo analizzando anche una macchina reversibile, abbiamo la possibilità di variare il segno dei valori di QR
e quindi di WR. Ora analizziamo infine il funzionamento di una macchina qualsiasi più quello di una macchina reversibile:

WR+Stot = WStot + WRtot =

= WStot - WRtot =

= QS2 – │QS1│- (QR2 – │QR1│) =

= │QR1│-│QS1│.

In tal caso la sorgente di calore più alta rimarrebbe inalterata, quindi ammetteremmo che la macchina sia in grado di lavorare grazie ad una sola sorgente di calore. Ciò come abbiamo visto e dimostrato è in contraddizione con l’enunciato di Lord Kelvin. Quindi arriviamo alla conclusione che una macchina reversibile ha sempre e comunque un rendimento maggiore di una non reversibile, nel caso che entrambi lavorino tra due eguali temperature.

 

Il ciclo di Carnot e il ciclo di Stirling

 

E sempre Carnot progettò una macchina che rappresenta una trasformazione ciclica, la quale appunto prende il suo nome.
Si tratta sostanzialmente di una serie di espansioni e compressioni isoterme ed adiabatiche che fanno compiere un lavoro alla macchina attraverso quatto diversi stadi:

1. Inizialmente abbiamo un’espansione isoterma, che traccia sul grafico un percorso da uno stato A ad uno stato B. Questo tipo di trasformazione è ottenuta mettendo il sistema a contatto con una sorgente di calore, di modo che la temperatura rimanga appunto costante, e diminuendo in modo quasistatico la pressione.

 

2. Segue un’espansione adiabatica, che dallo stato B prosegue allo stato C, tracciando sul grafico un percorso per così dire, più “vertiginoso”, dell’espansione isoterma, in quanto questa volta la temperatura diminuisce, dato che il sistema è completamente isolato dall’esterno, e quindi non è a contatto con fonti di calore con le quali mantenere la temperatura.

3. Per far tornare il sistema allo stato A di partenza, cominciamo col servirci di una compressione isoterma, mettendo il sistema a contatto con una sorgente di calore, che lo porta da uno stato C ad uno stato D.

 

4. Ed infine il ciclo si conclude con una compressione adiabatica. Come l’espansione, questa avviene in assenza di fonti di calore, e isolando completamente il sistema dall’esterno. Così continuiamo col diminuire il volume occupato dal gas, fino a che il sistema ritornerà allo stato A di partenza, esattamente con le stesse condizioni di partenza.

 

 

Alla fine il lavoro compiuto dal sistema durante il ciclo di Carnot sarà uguale all’area racchiusa tra gli archi di curva che verranno riportati sul grafico.

 

Simile è il ciclo di Stirling, il quale si basa su un eguale principio, ma in luogo delle trasformazioni ( espansioni e compressioni ) adiabatiche, troviamo delle trasformazioni isocore (volume costante):

• Tutto inizia con un’espansione isoterma, durante la quale, il sistema a contatto con una fonte di calore, assorbe calore (Q’2) e fa in modo che la temperatura rimanga costante.
• Segue una trasformazione isocora, durante la quale la pressione diminuisce, ed il sistema cede calore all’esterno ( Q’b = -cvm∆T).
• Come nel ciclo di Carnot, la terza è una compressione isoterma, che ci avvicina al punto iniziale, e a causa della quale il sistema continua a cedere calore ( Q’1).
• Infine, una trasformazione isocora, durante la quale la pressione aumenta ed il sistema acquisisce calore (Q’d = cvm∆T), riporta il sistema al punto di partenza, allo stato A, con identiche condizioni iniziali.

 

Un ostacolo da considerare però, nel ciclo di Stirling, è che per realizzare una trasformazione isocora, necessitano infinite fonti di calore.

Dall’esposizione del ciclo di Stirling possiamo dedurre che la prima e la quarta fase siano uguali ed opposte, quindi non fanno variare in alcun modo il valore ultimo del lavoro, che a questo punto sarà dato da:

W’ = Q’2 + Q’b + Q’1 + Q’d = Q’2 - cvm∆T = Q’2 – │Q’1│.

 

http://www.majorana-liceo.it/vecchio_sito/html/termod/relazione.doc
autore: non indicato nel documento di origine

 

---

 

Termodinamica

TERMODINAMICA (TRASFORMAZIONI DI CALORE IN LAVORO)

 

Lavoro di espansione

 

E’ noto che in meccanica il lavoro compiuto da una forza  costante F quando determina uno spostamento  DS di un corpo  è espresso da (1) L = FxS. Nel piano (F,S) il lavoro è rappresentato dall’area racchiusa sotto la curva .
Vogliamo determinare il lavoro compiuto da un gas quando si espande. Per analogia con la formula (1) tale lavoro sarà espresso analiticamente da:  L = pDV
Per dimostrare questa relazione si consideri un cilindro munito di stantuffo mobile senza attrito e contenente un fluido. Se A è la superficie del pistone e p è la pressione esercitata dal peso del pistone e dall’atmosfera esterna, il lavoro che il fluido deve compiere per sollevare il pistone di un tratto x contro le forze di pressione agenti dall’esterno risulta dato da:

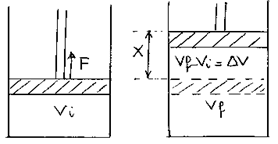
(2) L = FxS = PxAxX = PxDV

Oss 1. Dalla (2) si deduce che il lavoro compiuto in un’espansione (DV>0) è sempre positivo, ovvero lo stantuffo compie lavoro sull’ambiente esterno. Invece in una compressione (DV<0) il lavoro è negativo, ovvero è l’ambiente esterno a compiere lavoro sul sistema. Il lavoro è nullo se durante la trasformazione il volume rimane costante.

Oss2. Nella (2) p è la pressione esterna che contrasta il moto dello stantuffo. Il gas per contrastare tale pressione ne deve esercitare una di valore almeno uguale. Un processo nel quale le due pressioni sono uguali e che pertanto avviene in una successione di stati di equilibrio tali che, al termine di essa, il sistema possa essere riportato alle condizioni iniziali senza lasciare traccia nell’ambiente esterno si dice trasformazione reversibile, in caso contrario la trasformazione è detta irreversibile.

 

PRIMO PRINCIPIO DELLA TERMODINAMICA

 

Consideriamo il gas contenuto all’interno del cilindro munito di stantuffo, come la miscela aria-benzina all’interno del cilindro del motore di un’automobile. Riscaldiamo il gas (dall’esterno, oppure dall’interno innescando una scintilla se la miscela e’ esplosiva)
Il gas prima del riscaldamento si trovava ad una temperatura iniziale Ti. Le sue molecole hanno un’energia cinetica dovuta al loro movimento data dalla relazione Ec = 3/2NKTi ed una energia potenziale elettrica Eei dovuta alla presenza di forze di interazione di tipo elettrico tra cariche di segno opposto. La somma di queste energie si chiama Energia interna U = Ec + Ee . Se il gas è perfetto trascuriamo le interazioni di tipo elettrico e quindi Ui = Eci Dopo il riscaldamento e la conseguente espansione la sua temperatura è diventa Tf e la sua energia interna Uf. Sperimentalmente si osserva che lo scambio di energia (lavoro e calore) che il gas ha avuto con l'ambiente esterno è stato tale da verificare la seguente relazione nota come primo principio della termodinamica:
calore scambiato = variazione dell'energia interna + lavoro scambiato

(1)  Q = DU + L

• Questa relazione vale per qualunque sistema termodinamico cioè per qualunque insieme di corpi di cui si studiano gli scambi di energia  (entrate ed uscite), sotto forma di calore e lavoro, con l'ambiente esterno. Tuttavia viene generalmente utilizzato nello studio dei sistemi termodinamici gassosi poiché per i gas perfetti è possibile calcolare l'energia interna mediante formule semplici. Dal punto di vista delle energie scambiate, è possibile dunque giungere alla schematizzazione estrema della figura, tenendo presente la seguente convenzione: il calore è positivo se acquistato dal sistema, negativo se ceduto, il lavoro è positivo se fatto dal sistema, negativo se compiuto sul sistema.

 

• Il primo p. della td è a noi già familiare in quanto altro non è che il principio di conservazione dell'energia esteso al caso in cui sono coinvolti anche scambi di calore.

3) La quantità di calore e il lavoro  non sono  funzioni di stato nel senso che dipendono anche dal percorso seguito e non soltanto dagli stati iniziale 1 e finale 2. Invece  la quantità DU = Q-L , cioè l’energia interna, è del tutto indipendente dal percorso ma dipende solo dagli stati estremi 1 e 2 della trasformazione: è cioè una funzione di stato.
Ricordiamo che quando si parla di energia potenziale ciò che assume importanza non è il suo valore in un determinato punto, valore peraltro relativo e quindi privo di significato fisico, bensì le differenze di energia tra due punti distinti.

 

 

Il primo principio della Td nelle altre trasformazioni

In una trasformazione isobara cioè con p=cost  (fig. 4.7 a) abbiamo: Q = DU + L

 

Ora proponiamo una serie di esempi che illustrano le conseguenze della (1) nel caso di trasformazioni del gas diverse da quelle a p=cost:

 

 

 

 

• trasformazione a volume costante o isocora (fig.4.6) . Il gas non compie lavoro poiché non c'è variazione di volume (DV =0), quindi:  Q = DU. Un acquisto di calore aumenta l'energia interna e quindi la temperatura e la pressione, una cessione di calore diminuisce l'energia interna, la temperatura e la pressione. Essendo:

       Q = mcV(tf-ti) si ha anche  DU = mcV(tf-ti)

 

 

 

 

• trasformazione a temperatura costante o isotermica (fig 4.8).Non essendoci variazione di temperatura, l'energia interna rimane costante cioè DU=0 e quindi Q =L vale a dire che calore e lavoro hanno lo stesso segno. In una espansione isotermica il calore viene assorbito. Invece in una compressione isotermica il volume diminuisce, quindi il lavoro è negativo e anche il calore scambiato e negativo: il sistema cede calore all'ambiente.

 

 

 

 

• trasformazione che non scambia calore con l’esterno o adiabatica: Le pareti del recipiente contenente il gas non consentono alcuno scambio di calore con l'esterno Il gas è termicamente isolato, essendo Q =0 si ha che  DU = -L. In una espansione adiabatica il volume aumenta DV>0 quindi il lavoro è positivo, allora l'energia interna, e quindi la temperatura, diminuiscono e pertanto il gas effettua un lavoro a spese dell'energia interna. Da notare che, contrariamente a quanto si potrebbe pensare, un esempio tipico di espansione adiabatica è l'esplosione della miscela nei motori a scoppio. La corsa del pistone spinto dalle forze di pressione del gas è talmente rapida che il gas non ha tempo di scambiare calore con l'esterno. In una compressione adiabatica, invece, il volume diminuisce quindi il lavoro è negativo e pertanto l'energia interna e la  temperatura aumentano.

Il grafico di una trasformazione adiabatica in un diagramma P-V è rappresentato da una curva simile ad un'iperbole ma più pendente di quella relativa ad una trasformazione isoterma poiché la sua equazione è:

      PV g = cost          dove g è una grandezze adimensionale caratteristica del gas e vale g = Cp/Cv 

Oss1. Nei gas bisogna distinguere tra calore specifico a pressione costante Cp e quello a volume costante Cv. Risulta che Cp è sempre maggiore di Cv ed inoltre se il gas è monoatomico g=5/3 mentre se è biatomico g = 7/5

 

Fonte: http://www.fisicaweb.org/doc/termodinamica/termodinamica.doc
Autore: non indicato nel documento di origine

 

 

Termodinamica

 

A cura di Eugenio Amitrano

 

1. DEFINIZIONI

Sistema termodinamico:
Qualsiasi porzione dell’universo può essere considerato un sistema termodinamico. Questa porzione di spazio ha un confine, una superficie di controllo che lo separa dal resto dell’universo (ambiente). Questo confine può essere costituito da qualcosa di reale (per esempio un contenitore) oppure può essere puramente immaginario. In funzione della natura del confine e pertanto dalle relazioni che il sistema ha con l’ambiente, possiamo classificare un sistema termodinamico in 3 grandi categorie:

Sistema aperto: se il sistema consente uno scambio sia di materia che di energia con l’ambiente; Ad esempio, una pentola di acqua calda senza il coperchio oltre a dissipare calore nell’ambiente, perde anche particelle di acqua attraverso il vapore acqueo.

Sistema chiuso: se il sistema consente uno scambio di energia con l’ambiente ma non di materia; Ad esempio, se mettiamo il coperchio alla pentola del precedente esempio, evitiamo la fuoriuscita del vapore acqueo, per cui con l’ambiente scambia solo energia (in questo caso il calore)

Sistema isolato: se il sistema NON consente scambi di energia e materia con l’ambiente. Ad esempio un thermos di acqua calda, idealmente è un sistema isolato, poiché oltre ad evitare la fuoriuscita di vapore acqueo, evita anche la dispersione del calore mantenendo così l’acqua sempre calda.

Stato termodinamico:
Un sistema termodinamico è valutato in funzione del valore di tre parametri macroscopici fondamentali, che sono temperatura, pressione e volume. Lo stato termodinamico è rappresentato dall’insieme dei valori assunti da questi parametri che quindi caratterizzano il sistema.
Poiché temperatura, pressione e volume di un sistema sono legati in maniera univoca, basta considerare solo 2 di questi parametri per ottenere il terzo. Ad esempio per ogni pressione e volume corrisponde una ed una sola temperatura. Generalmente, per indicare uno stato termodinamico, si preferisce fare riferimento proprio a pressione e volume, riportando così un generico stato termodinamico in un diagramma, detto propriamente diagramma P-V (P e V indicano pressione e volume).

Trasformazione termodinamica:
É un qualsiasi processo tramite il quale un sistema termodinamico passa da uno stato termodinamico (detto iniziale) ad un altro (detto finale).

Trasformazione irreversibile:
È una qualsiasi trasformazione spontanea, cioè che lo stato termodinamico di partenza, stato iniziale, si trova in una condizione di NON equilibrio. Questo vuol dire che la trasformazione avviene per raggiungere la condizione di equilibrio, per esempio per una trasformazione che vede la liberazione di un gas sotto pressione nell’atmosfera, l’equilibrio viene raggiunto nel momento in cui la pressione interna del gas eguaglia la pressione atmosferica.

Trasformazione reversibile:
La trasformazione reversibile, possibile solo idealmente, è quel tipo di trasformazione in qui ogni stato intermedio si trova sempre in equilibrio. Per esempio quando una pressione esterna esercitata su un gas diminuisce così lentamente che la pressione interna del gas è sempre pari alla pressione esterna.

Funzione di stato:
È una grandezza fisica o proprietà di un sistema che dipende solamente dallo stato iniziale e finale, e non dal particolare cammino seguito per arrivarvi. Per esempio l’energia potenziale di un oggetto, assodato che l’oggetto conserva sempre la stessa massa e che l’accelerazione di gravità è costante, dipende esclusivamente dall’altezza in cui si trova rispetto al suolo, indipendentemente dal percorso fatto per raggiungere quell’altezza. Un uomo sul tetto di un grattacielo, indipendentemente se ha raggiunto il tetto attraverso le scale, o arrampicandosi come spiderman, avrà acquisito la stessa energia potenziale.

 

10. Riferimenti e fonti

• Wikipedia, http://it.wikipedia.org/wiki/Pagina_principale

 

Autore: Eugenio Amitrano
Fonte: http://www.atuttoportale.it/Downloads/Formulari/FormularioTermodinamica.doc

 

LA TERMODINAMICA

 

La termodinamica è quella branca della fisica e della chimica (chimica fisica) che descrive le trasformazioni subite da un sistema in seguito a processi che coinvolgono la trasformazione di calore in lavoro e viceversa.
La termodinamica classica si basa sul concetto di sistema macroscopico, ovvero una porzione di materia fisicamente o concettualmente separata dall'ambiente esterno, che spesso per comodità si assume non perturbato dallo scambio di energia con il sistema. Lo stato di un sistema macroscopico che si trova all'equilibrio è specificato da grandezze dette variabili termodinamiche o di stato come la temperatura, la pressione, il volume, la composizione chimica. Tuttavia esiste una branca della termodinamica, denominata Termodinamica del non equilibrio che studia i processi termodinamici non-lineari caratterizzati dal mancato raggiungimento di condizioni di equilibrio stabile. Fu Sadi Carnot nel 1824 il primo a dimostrare che si può ottenere lavoro dallo scambio di calore tra due sorgenti a temperature differenti. Attraverso il teorema di Carnot e la macchina ideale di Carnot quantificò questo lavoro e introdusse il concetto di rendimento termodinamico.
Nel 1848 Lord Kelvin utilizzando la macchina di Carnot introdusse il concetto di temperatura termodinamica assoluta e a lui si deve un enunciato del secondo principio della termodinamica. Nel 1850 Joule dimostra l'uguaglianza delle due forme di energia (allora si credeva esistesse ancora il fluido calorico). A questo punto si era posto il problema che se era possibile ottenere calore dal lavoro in modo totale, non era possibile ottenere l'inverso. A questo risultato approda anche Clausius che nel 1855 introdusse la sua disuguaglianza per riconoscere i processi reversibili da quelli irreversibili e la funzione di stato entropia. Un sistema termodinamico è una porzione di spazio, separata dal resto dell’universo (cioè l’ambiente esterno) mediante una superficie di controllo (superficie reale o immaginaria, rigida o deformabile), sede di trasformazioni interne e scambi di materia o energia con l’ambiente esterno. I suddetti scambi possono avvenire sotto forma di calore o lavoro. Questi due concetti non sono delle proprietà intrinseche del sistema, ma sussistono nel momento in cui esso interagisce con l'ambiente, cioè scambia energia con l'esterno. Quindi un sistema non possiede calore o lavoro, bensì energia; ogni variazione di energia è poi esprimibile in termini di calore (se il passaggio di energia è dovuto ad una differenza di temperatura tra ambiente e sistema) e lavoro (per qualunque variazione energetica che non sia dovuta alla differenza di temperatura, come ad es. una forza meccanica che provochi uno spostamento, un trasferimento di energia elettrica o elastica).
I bordi dei sistemi termodinamici si possono classificare nel modo seguente:

• Sulla base dello scambio di calore in:
• Bordi adiabatici, se non consentono lo scambio di calore;
• Bordi diatermani, se invece lo consentono;

• Sulla base dello scambio di lavoro in:
• Bordi rigidi, se non consentono lo scambio di lavoro;
• Bordi flessibili, se invece lo consentono;

• Sulla base dello scambio di materia in:
• Bordi permeabili, se consentono il passaggio di ogni specie chimica
• Bordi semipermeabili, se consentono il passaggio di alcune specie chimiche
• Bordi impermeabili, se invece non consentono il passaggio di alcuna specie chimica.

Si possono distinguere vari tipi di sistemi, in dipendenza dal modo di scambiare energia con l'esterno:

• sistemi isolati: non scambiano calore, materia, lavoro con l'esterno (bordi impermeabili, rigidi e adiabatici);
• sistemi chiusi: scambiano energia (calore, lavoro), ma non materia con l'esterno. Quando un sistema scambia calore, lavoro o entrambi, lo si può classificare in base alle proprietà al bordo che sarà:
• impermeabile
• rigido o flessibile
• adiabatico o diatermano
• sistemi aperti: permettono scambio di energia e materia con l'esterno (cioè bordi permeabili o semipermeabili, diatermi e flessibili).

Coordinate termodinamiche
Le proprietà termodinamiche usate per descrivere un sistema sono dette coordinate termodinamiche. Dato un certo numero di coordinate, esse possono essere:

• indipendenti, se è possibile modificare il valore di ciascuna di esse senza determinare una variazione del valore delle altre;
• dipendenti, se variando il valore di una di esse anche le altre coordinate vengono modificate.

E' tipica della termodinamica la distinzione fra proprietà estensive ed intensive:

• estensive, se dipendono dalle dimensioni del sistema (ad es. massa, volume, capacità termica);
• intensive, se non dipendono dalle dimensioni del sistema (ad es. pressione e temperatura);
• specifiche: rapportando una proprietà estensiva con le dimensioni del sistema (tipicamente la massa, ma anche il numero di moli o il volume) si ottiene una proprietà intensiva che è detta la corrispondente specifica della proprietà estensiva corrispondente: volume specifico, densità ("massa specifica"), calore specifico...

Secondo un noto postulato di stato, date due proprietà intensive indipendenti, lo stato di un sistema semplice risulta completamente determinato.
Temperatura, volume, pressione e numero di moli sono i tipici esempi di coordinate termodinamiche.
Trasformazioni termodinamiche
Quando un sistema passa da uno stadio di equilibrio ad un altro, si dice che avviene una trasformazione termodinamica: si distingue tra trasformazioni reversibili, ovvero quelle trasformazioni che consentono di essere ripercorse in senso inverso (si ritorna precisamente al punto di partenza, ripercorrendo all'indietro gli stessi passi dell'andata), e trasformazioni irreversibili, ovvero quelle trasformazioni che, se ripercorse all'indietro, non faranno ritornare al punto iniziale, ma ad uno diverso. Perché una trasformazione sia reversibile è necessario che essa avvenga abbastanza lentamente da permettere al sistema di termalizzare (il sistema deve passare attraverso infiniti stati di equilibrio termodinamico). Le trasformazioni termodinamiche possono essere anche dei seguenti tipi:

• Isobare: se la pressione si mantiene costante;
• Isocore, se il volume si mantiene costante (e il lavoro scambiato tra sistema ed esterno è dunque nullo);
• Isoterme, se la temperatura si mantiene costante;
• Adiabatiche, se il calore totale scambiato è nullo;
• Isoentropiche, o adiabatiche reversibili, se la variazione di entropia è nulla;

I Principi della Termodinamica
I principi della termodinamica vennero enunciati nel corso del diciannovesimo secolo e regolano le trasformazioni termodinamiche, il loro procedere, i loro limiti. Sono dei veri e propri assiomi, non dimostrati e indimostrabili, fondati sull'esperienza, sui quali si fonda tutta la teoria che riguarda la termodinamica.
Si possono distinguere tre principi di base più un principio zero che definisce la temperatura, e che è implicito negli altri tre.

Principio Zero
Quando due sistemi interagenti sono in equilibrio termico, condividono alcune proprietà, che possono essere misurate dando loro un preciso valore numerico. In conseguenza, quando due sistemi sono in equilibrio termico con un terzo, sono in equilibrio tra loro e la proprietà condivisa è la temperatura. Il principio zero della termodinamica dice semplicemente che, se un corpo "A" è in equilibrio termico con un corpo "B" e "B" è in equilibrio termico con un corpo "C", "A" e "C" sono in equilibrio tra loro.
Tale principio spiega il fatto che due corpi a temperature diverse, tra cui si scambia del calore, (anche se questo concetto non è presente nel principio zero) finiscono per raggiungere la stessa temperatura. Nella formulazione cinetica della termodinamica, il principio zero rappresenta la tendenza a raggiungere un'energia cinetica media comune degli atomi e delle molecole dei corpi tra cui avviene scambio di calore: in media, come conseguenza degli urti delle particelle del corpo più caldo, mediamente più veloci, con le particelle del corpo più freddo, mediamente più lente, si avrà passaggio di energia dalle prime alle seconde, tendendo dunque ad uguagliare le temperature. L'efficienza dello scambio di energia determina i calori specifici dei materiali coinvolti.

Primo Principio
Quando un corpo viene posto a contatto con un altro corpo relativamente più freddo, avviene una trasformazione che porta a uno stato di equilibrio, in cui sono uguali le temperature dei due corpi. Per spiegare questo fenomeno, gli scienziati del diciottesimo secolo supposero che una sostanza, presente in maggior quantità nel corpo più caldo, passasse nel corpo più freddo. Questa sostanza ipotetica, detta calorico, era pensata come un fluido capace di muoversi attraverso la materia. Il primo principio della termodinamica invece identifica il calore come una forma di energia che può essere convertita in lavoro meccanico ed essere immagazzinata, ma che non è una sostanza materiale. È stato dimostrato sperimentalmente che il calore, misurato originariamente in calorie, e il lavoro o l'energia, misurati in joule, sono assolutamente equivalenti. Ogni caloria equivale a 4,186 joule. Il primo principio è dunque un principio di conservazione di energia. In ogni macchina termica una certa quantità di energia viene trasformata in lavoro: non può esistere nessuna macchina che produca lavoro senza consumare energia. Una simile macchina, se esistesse, produrrebbe infatti il cosiddetto moto perpetuo di prima specie. Il primo principio viene tradizionalmente enunciato come "In un sistema chiuso si ha che ΔU = Δq - Δw dove U è l'energia interna del sistema. Per Energia Interna si intende la somma delle energie cinetiche e di interazione delle diverse particelle di un sistema. Δq è il calore scambiato tra ambiente e sistema (positivo se fornito al sistema, negativo se invece ceduto dal sistema) e Δw il lavoro compiuto (positivo se compiuto dal sistema sull'ambiente, negativo invece se compiuto dall'ambiente sul sistema). La convenzione dei segni risente del legame con lo studio dei motori termici, nei quali il calore viene trasformato (parzialmente) in lavoro.
Formulazioni alternative ed equivalenti del primo principio sono:

• Per un sistema aperto, q-w=ΔE, ove per ΔE si intende la variazione di energia totale, che altro non è che la somma delle variazioni dell'energia interna , dell'energia cinetica e dell'energia potenziale possedute da quel sistema. Si vede che per un sistema chiuso le variazioni di energia cinetica e potenziale sono nulle per cui ci si riconduce alla relazione precedente.
• Per un ciclo termodinamico, q=w, dal momento che la variazione di energia totale è nulla, dovendo il sistema, al termine di ogni ciclo, ritornare nelle stesse condizioni di partenza.

Esempio del primo principio

 

Secondo Principio
Esistono diversi enunciati del secondo principio, tutti equivalenti, e ciascuna delle formulazioni ne mette in risalto un particolare aspetto. Esso afferma che è impossibile realizzare una macchina ciclica che abbia come unico risultato il trasferimento di calore da un corpo freddo a uno caldo o, equivalentemente, che è impossibile costruire una macchina ciclica che operi producendo lavoro a spese del calore sottratto a una sola sorgente. Quest'ultima limitazione nega la possibilità di realizzare il cosiddetto moto perpetuo di seconda specie. L’entropia  totale di un sistema isolato rimane invariata quando si svolge una trasformazione reversibile ed aumenta quando si svolge una trasformazione irreversibile.
Terzo Principio
È strettamente legato al secondo, e in alcuni casi è considerato come una conseguenza di quest'ultimo. Può essere enunciato dicendo che è impossibile raggiungere lo zero assoluto con un numero finito di trasformazioni e fornisce una precisa definizione della grandezza chiamata entropia. Esso afferma inoltre che l'entropia per un solido perfettamente cristallino, alla temperatura di 0 Kelvin è pari a 0. È facile spiegare questo enunciato tramite la termodinamica molecolare: un solido perfettamente cristallino è composto da un solo complessioma (sono tutti i modi di disporre le molecole, se le molecole sono tutte uguali indipendentemente da come sono disposte, macroscopicamente il cristallo è sempre uguale) e, trovandosi a 0 Kelvin, l'energia vibrazionale, traslazionale e rotazionale delle particelle che lo compongono è nulla, per cui, dalla legge di Bolzmann S = k ln(1) = 0 dove 1 sono i complessiomi (in questo caso uno solo).

 

Progetto di Federica Pucinotti

Fonte: http://www.francescozumbo.it/zumbo/lavori-studenti/2008/cd-5g-2007-2008/lavori/pucinotti-Termodinamica-5g.rtf

Sito web da visitare: http://www.francescozumbo.it/

 

Termodinamica

 

 

Visita la nostra pagina principale

 

Termodinamica

 

Termini d' uso e privacy