Test di geometria

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Test di geometria

Test di Geometria

1. Se ogni coppia di numeri seguenti rappresenta le coordinate cartesiane di un punto qual è quello più lontano dall'origine?

A) 2;5

B) 0;7

C) 4;4

D) 6;1

E) 5;2

2. Nel piano x,y le due equazioni y = -6 e y = x² rappresentano:

A) una retta e una parabola che non si incontrano

B) una retta e un'iperbole che non si incontrano

C) una retta e una parabola che si incontrano in due punti

D) una retta e un'iperbole che si incontrano in due punti

E) una retta e un'ellisse che si incontrano in due punti

3. Data l'equazione generica della retta y = mx + q, quale delle seguenti condizioni deve verificarsi affinché la retta non passi assolutamente per il quarto quadrante?

A) m < 0, q < 0

B) m > 0, q > 0

C) m > 0, q < 0

D) m < 0, q > 0

E) m > 0, q diverso da 0

4. Di due cerchi, il primo ha area doppia del secondo. Qual è il rapporto tra la lunghezza della circonferenza del primo e quella della circonferenza del secondo?

A) 2

B) 2p

C) p

D) 21/2

E) 1/2

5. 100 mm3 equivalgono a:

A) 10^-7 m3

B) 10^-1 m3

C) 10^-4 m3

D) 10⁷ m3

E) 1 m3

6. Due rette di equazioni y = mx + p e y = nx + q sono tra loro sempre parallele se:

A) m - n = 0

B) m + n = 1

C) m + n = -1

D) m + n = 0

E) m - n = 1

7. Due triangoli sono necessariamente uguali quando sono uguali:

A) le tre coppie di angoli

B) un angolo ed il lato opposto

C) due lati e l'angolo opposto ad uno di essi

D) due lati e l'angolo compreso tra essi

E) due lati e la somma degli angoli interni

8. Quale delle seguenti terne di numeri può rappresentare le misure dei lati di un triangolo?

A) 3 4 6

B) 1 2 4

C) 1 2 5

D) 2 4 7

E) 1 2 6

9. Le due rette y = mx e y = x/m sono parallele quando:

A) m² = 1

B) m + 1/m = 1

C) m + 1/m = -1

D) m + 1/m = 0

E) m - 1/m = 1

10. Nel piano x,y le due equazioni y = 6, y = x² rappresentano:

A) una retta e una parabola che si incontrano in un punto

B) una retta e una parabola che non si incontrano

C) una retta e una parabola che si incontrano in due punti

D) una retta e una parabola tangenti

E) una situazione diversa dalle precedenti

11. Trovare la differenza tra il volume di un cilindro di altezza 2r e raggio r ed il volume della sfera inscritta di uguale raggio:

A) 3/2 p r³

B) p r³

C) 2/3 p r³

D) 1/3 p r³

E) 4/3 p r²

12. Nel piano, due rette sono parallele quando:

A) hanno un punto in comune

B) sono perpendicolari alla stessa retta

C) formano un angolo ottuso

D) formano un angolo acuto

E) si incontrano solo in un punto

13. Considerando le misure di un lato e della relativa altezza di un triangolo, l'area è uguale:

A) alla loro semisomma

B) al loro semiprodotto

C) alla loro somma

D) al loro prodotto

E) al doppio del loro prodotto

14. Quale dei seguenti poligoni regolari inscritti nello stesso cerchio ha l'area maggiore?

A) Esagono

B) Quadrato

C) Triangolo

D) Pentagono

E) Le aree sono tutte uguali

15. Quali sono le coordinate dei punti di intersezione della curva di equazione y² = x + 24 con la retta di equazione x = 1?

A) (1,5) (1,- 5)

B) (1,5/2) (1,-5/2)

C) (1,5/4) (1,-5/4)

D) (1,25) (1,-25)

E) Coordinate diverse da quelle delle precedenti risposte

16. Se A e B sono due quadrilateri quale affermazione è sempre VERA?

A) A ha quattro lati e B non è un triangolo

B) A e B sono parallelogrammi

C) A e B sono poligoni regolari

D) La somma di A e B è un quadrilatero

E) La somma degli angoli interni di A e di quelli di B è 360°

17. Due triangoli sono simili. Le lunghezze dei lati del triangolo più piccolo sono uguali al 50% delle lunghezze dei corrispondenti lati del triangolo più grande. L'area del triangolo piccolo rispetto a quella del triangolo grande è il:

A) 25%

B) 50%

C) 75%

D) 2,5%

E) 5%

18. Qualsiasi triangolo che sia inscritto in una circonferenza e abbia un lato coincidente con un diametro della circonferenza è:

A) scaleno

B) isoscele

C) equilatero

D) rettangolo

E) ottusangolo

19. Il coefficiente angolare di una retta è:

A) l'angolo formato dalla retta e dall'asse delle ascisse espresse in radianti

B) l'angolo formato dalla retta e dall'asse delle ascisse espresso in gradi

C) il valore della tangente trigonometrica dell'angolo formato dalla retta con l'asse delle ascisse

D) il valore del coseno dell'angolo formato dalla retta con l'asse delle ascisse

E) nessuna delle precedenti risposte è corretta

20. In un piano cartesiano l'equazione y = x rappresenta:

A) una retta parallela all'asse y

B) una retta parallela all'asse x

C) un punto del piano

D) la bisettrice del I e III quadrante

E) la bisettrice del II e IV quadrante

21. Con tre segmenti di lunghezze rispettive 1 cm, 2 cm, 4 cm:

A) non è possibile costruire un triangolo

B) è possibile costruire un triangolo rettangolo

C) è possibile costruire un triangolo ottusangolo

D) è possibile costruire un triangolo scaleno

E) è possibile costruire un triangolo isoscele

22. La parabola y = x² ha per vertice il punto:

A) (0,0)

B) (2,2)

C) (1,1)

D) (0,1)

E) (1,0)

23. Un triangolo rettangolo ha un'area di 10 cm²; i suoi lati valgono:

A) 1 cm, 20 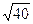cm, cm

B) 2 cm, 10 cm, cm

C) 4 cm, 5 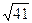cm, cm

D) 3 cm, 4 cm, 5 cm

E) 2 cm, 5 cm, cm

24. La terna di numeri 4, 5, 10 rappresenta le lunghezze dei lati di:

A) un triangolo acutangolo

B) un triangolo rettangolo e isoscele

C) un triangolo ottusangolo

D) nessun triangolo

E) un triangolo rettangolo non isoscele

25. Nel piano cartesiano i due punti di coordinate (0,0) e (3,4) hanno distanza:

A) 7

B) 5

C) 1

D) 12

E) 25

26. L'area di un cerchio di raggio unitario è uguale a:

A) 1/2 p

B) p

C) p 2

D) 2 p

E) 4/3 p

27. Quali sono le coordinate dei punti di intersezione della curva 2y² = 3x + 8 con l'asse delle y?

A) (0,2) (0,-2)

B) (0,2) (-2,0)

C) (2,0) (-2,0)

D) (2,0) (0,-2)

E) (0,2) (0,2)

28. A quanti radianti corrispondono 90°?

A) 1/2

B) 1

C) 2/3

D) 2

E) Un numero diverso da quelli delle precedenti risposte

29. Un campo di forma circolare ha perimetro di 4000 metri. La misura della lunghezza di una palizzata esterna che lo circondi a distanza di un metro dal bordo è, in metri:

A) più di 4000 p

B) 4000 + p

C) 4000 + 2 p

D) 1 + 4000/ p

E) 1 + 4000/2 p

30. Qual è il rapporto fra l'area di un cerchio di raggio unitario e l'area del quadrato inscritto?

A) p

B) p 2

C) p /2

D) p - 2

E) 2 p

31. Un triangolo rettangolo ha un angolo di 60°. Quanti gradi vale l'altro angolo acuto?

A) 40°

B) 90°

C) 60°

D) 30°

E) Non si può dire con le informazioni date

32. Perché due triangoli isosceli siano simili, basta che:

A) un lato di uno sia uguale a un lato dell'altro

B) un'altezza di uno sia uguale a un'altezza dell'altro

C) due lati di uno siano uguali a due lati dell'altro

D) un angolo di uno sia uguale a un angolo dell'altro

E) nessuna delle condizioni precedenti è sufficiente

33. La curva che nel piano x,y ha equazione x² + y² = r² e:

A) una retta

B) una circonferenza

C) una parabola

D) un'ellisse

E) un'iperbole

34. La retta y = k + h . x è la bisettrice del primo quadrante degli assi cartesiani:

A) sempre

B) solo per k = 1 ed h = 0

C) solo per k = 0 ed h = 1

D) solo per k = 1 ed h = 1

E) mai

35. La retta di equazione y = 3x:

A) è parallela all'asse x

B) passa per il punto P (2,6)

C) non passa per l'origine

D) è parallela all'asse y

E) è la bisettrice del primo quadrante

36. Quale dei seguenti punti non giace sulla retta di equazione y = 2x + 1?

A) (1,3)

B) (0,1)

C) (-1,-1)

D) (-1,1)

E) (2,5)

37. Quale delle seguenti equazioni rappresenta una curva passante per l'origine?

A) y = 3x - 3

B) y = x² - 1

C) y = 2

D) y = x²

E) x = 3

38. Due triangoli rettangoli sono uguali se, oltre all'angolo retto, hanno uguali (congruenti):

A) le ipotenuse

B) un cateto

C) i due angoli acuti

D) un lato qualsiasi

E) i due cateti

39. Un cono circolare retto è secato da due piani perpendicolari all'asse, che distano dal vertice rispettivamente 2 e 6 metri. Il rapporto tra le aree delle intersezioni del cono coi due piani è:

A) 3

B) 9

C) 4

D) p

E) determinato dall'apertura del cono

40. L'equazione di una retta nel piano cartesiano è y = a + bx. Il coefficiente b definisce:

A) una misura della pendenza della retta

B) l'intersezione con l'asse y

C) il valore di y per x = 0

D) il valore di y per x = 1

E) dipende dal valore di b

41. La rappresentazione grafica della funzione f(x) = (12 - 4x)² è una:

A) retta con pendenza negativa

B) circonferenza di centro (3,0)

C) ellisse con i fuochi sull'asse delle x

D) parabola con la concavità rivolta verso il basso

E) parabola con la concavità rivolta verso l'alto

42. Se abbiamo una sfera ed un cubo di uguale volume, la superficie della sfera è:

A) minore di quella del cubo

B) uguale a quella del cubo

C) non sono noti elementi per rispondere

D) le superfici non sono fra loro comparabili

E) metà di quella del cubo

43. La somma degli angoli di un quadrilatero è uguale a:

A) 180°

B) 360°

C) 90°

D) 720°

E) non è costante

44. Quale delle rette disegnate in figura è rappresentata dall'equazione y - x + 3 = 0?

A) 1

B) 2

C) 3

D) 4

E) 5

45. Una piramide viene tagliata da due piani paralleli, ad una distanza dal vertice, misurata lungo l'altezza della piramide, una di 2 m e l'altra di 4 m. Quale sarà il rapporto tra le aree intersecate dai due piani?

A) 1/2 p

B) 1/4 p

C) 1/2

D) 1/4

E) Dipende dall'altezza della piramide

46. Per caratterizzare un triangolo, è necessario conoscerne alcuni elementi (quali angoli, lati, ecc.). Quale dei seguenti insiemi di elementi NON consente di caratterizzare un unico triangolo?

A) Un lato e gli angoli ad esso adiacenti

B) Un lato, un angolo ad esso adiacente, e l'angolo ad esso opposto

C) Due lati e l'angolo compreso

D) I tre lati

E) I tre angoli

47. Due rette di equazioni y = mx e y = nx sono tra loro sempre perpendicolari se:

A) m . n = - 1

B) m . n = 1/2

C) m = n

D) m . n = 1

E) m . n = - 1/2

48. Due sfere hanno raggi di lunghezza l'una tripla dell'altra. Quale è il rapporto tra la misura del volume della sfera di raggio maggiore e quella del volume della sfera di raggio minore?

A) 3

B) p

C) 9

D) 3 p

E) 27

49. Le curve di equazione y = ax² + bx + c (parabole) intersecano l'asse delle ascisse:

A) in due punti

B) in un punto

C) in nessun punto

D) in un numero di punti che dipende dai valori di a, b, c

E) in un numero di punti che dipende solo dal valore di a

50. La parabola di equazione y = 4 - x²:

A) non taglia l'asse x

B) è tangente all'asse x

C) taglia l'asse x in due punti simmetrici rispetto all'origine

D) taglia l'asse x in due punti entrambi di ascissa positiva

E) taglia l'asse x in due punti entrambi di ascissa negativa

51. Un cono e un cilindro circolari retti hanno uguale altezza e il raggio di base del cono uguale al diametro del cilindro. Detto V il volume del cono e W il volume del cilindro, il rapporto V/W è:

A) = 4/3

B) = 1

C) = 3/4

D) = 2

E) dipendente dal raggio

52. Il rapporto tra la misura del volume e la misura della superficie di una sfera di raggio r è:

A) p

B) p r

C) r/3

D) r²

E) r

53. In qualunque triangolo, dette a, b, c le misure dei lati, è:

A) c² = a² + b²

B) c > a + b

C) c < a + b

D) c² > a² + b²

E) c = a + b

54. Un angolo di 360° sessagesimali, espresso in radianti è uguale approssimativamente a:

A) 2 radianti

B) 3,14 radianti

C) 4 radianti

D) 6,28 radianti

E) 1/3,14 radianti

55. Lo spigolo di un cubo ha lunghezza 10 mm. Il volume del cubo, in m³, ha misura:

A) 3 . 10^-5

B) 10^-15

C) 100

D) 10^-3

E) 10^-6

56. Perché due triangoli isosceli siano simili basta che:

A) abbiano la stessa base

B) abbiano la stessa altezza

C) abbiano lo stesso angolo al vertice

D) sono sempre simili

E) abbiano la stessa area

57. La somma degli angoli interni di un esagono non regolare:

A) è pari a 720°

B) è pari a 600°

C) dipende dalla lunghezza dei lati

D) dipende dalla forma del poligono

E) è pari a 360°

58. La rappresentazione grafica delle due equazioni x = y e x + y = 2 dà:

A) due rette che si intersecano nei punti (1,1) e (0,0)

B) due rette che non si intersecano

C) due rette che si intersecano nel punto (0,2)

D) due rette che si intersecano nel punto (2,0)

E) due rette che si intersecano nel punto (1,1)

59. La misura in radianti di un angolo di 60° è:

A) p /2

B) p /3

C) 2 p /3

D) non esprimibile perché il radiante non è una misura degli angoli

E) p /4

60. Un quadrato ha il lato L uguale al raggio di una circonferenza. Il rapporto fra il perimetro del quadrato e la misura della circonferenza risulta:

A) > 1

B) < 1

C) = 1

D) dipendente dal valore che assume L

E) uguale a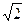

61. La curva che nel piano x,y ha equazione y = 5x + 7 è:

A) un'ellisse

B) un'iperbole

C) una circonferenza

D) una retta

E) una parabola

62. È vero che:

A) un trapezio è equivalente ad un rettangolo di uguale altezza e con base uguale alla semisomma delle basi del trapezio

B) un trapezio è equivalente ad un rettangolo di uguale altezza e con base uguale alla somma delle basi del trapezio

C) due figure equivalenti sono sempre uguali

D) un trapezio non può mai essere equivalente a un rettangolo

E) nessuna delle precedenti affermazioni è corretta

63. Se la somma delle misure in gradi degli angoli interni di un triangolo piano è 210°, il triangolo:

A) è ottusangolo

B) è acutangolo

C) è equilatero

D) non esiste

E) ha almeno un angolo retto

64. La funzione x + y = K rappresenta sul piano cartesiano:

A) una circonferenza

B) un'iperbole

C) una retta

D) un'ellisse

E) una parabola

65. Una retta forma con l'asse x un angolo di +45° e incontra l'asse y nel punto di coordinate (0, -3). L'equazione della retta è:

A) y = -x + 3

B) y = -x - 3

C) y = x - 3

D) y = x + 3

E) y = -3

66. La retta di equazione x - y = 3 interseca la retta x + y = 1 nel punto di coordinate:

A) (0, 0)

B) (1, 2)

C) (2, -1)

D) (-1, 2)

E) le rette sono parallele

67. La retta di equazione y = 3x + 2 interseca l'asse delle x in un punto:

A) di ascissa negativa

B) di ascissa positiva

C) di ascissa nulla

D) di ascissa uguale 2/3

E) non interseca l'asse delle ascisse

68. Quale dei seguenti poligoni regolari di lato uguale ha l'area maggiore?

A) Ottagono

B) Pentagono

C) Quadrato

D) Triangolo

E) Le aree sono tutte uguali

69. La misura di una diagonale di un quadrato si può ottenere:

A) dividendo la misura del lato per la radice quadrata di 2

B) moltiplicando la misura del lato per la radice quadrata di 2

C) facendo la differenza tra la misura di due lati

D) moltiplicando per 4 il rapporto tra la lunghezza di due lati

E) soltanto misurandola

70. Due cerchi hanno raggi di lunghezza l'una tripla dell'altra. Quale è il rapporto tra la misura della superficie del cerchio di raggio maggiore e quella della superficie del cerchio di raggio minore?

A) 3

B) p

C) 9

D) 3 p

E) 27

71. I punti di coordinate cartesiane (3,2); (6,4); (9,6):

A) possono rappresentare i vertici di un triangolo rettangolo

B) possono rappresentare i vertici di un triangolo scaleno

C) sono allineati

D) sono equidistanti dall'origine del piano cartesiano

E) individuano una parabola

72. Se il raggio di una sfera si raddoppia, il suo volume:

A) si raddoppia

B) aumenta di 4 volte

C) aumenta di 9 volte

D) aumenta di 8 volte

E) si moltiplica per 27

73. Una circonferenza è un caso particolare di:

A) parabola

B) iperbole

C) ellisse

D) retta

E) terna di rette

74. Una retta passante per l'origine degli assi e che forma con il semiasse positivo delle ascisse un angolo di 120° ha equazione:

A) y = -x +

B) y = -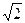 . x

C) y = - . x

D) y = . x

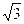E) y = - . x

75. Nel piano x,y le equazioni y = x + 1 e y = x + 3 rappresentano:

A) due rette che si intersecano nel punto (1,3)

B) due rette che si intersecano nell'origine

C) due rette perpendicolari

D) due rette parallele

E) due rette coincidenti

76. Si definisce luogo dei punti equidistanti da due punti A e B:

A) la circonferenza avente AB come diametro

B) l'ellisse avente A e B come fuochi

C) l'iperbole avente A e B come fuochi

D) l'asse del segmento AB

E) la circonferenza avente AB come raggio

77. Le curve di equazione x² + y² + ax + by + c = 0 individuano una particolare circonferenza quando:

A) sono note le coordinate del centro e quelle di un punto

B) sono note le coordinate di due punti

C) è noto il raggio

D) sono note le coordinate dei punti di intersezione con l'asse x

E) sono note le coordinate dei punti di intersezione con l'asse y

78. Dati due cerchi tali che l'area del primo sia doppia dell'area del secondo, in quale rapporto sta la lunghezza della circonferenza del primo rispetto alla lunghezza della circonferenza del secondo?

A) 2

B) 21/2

C) p

D) 2-1/2

E) 1/2

79. Il numero p (3,1416...) è il rapporto tra:

A) la circonferenza e il raggio

B) l'area del cerchio e il quadrato del diametro

C) l'area del cerchio e il diametro

D) la circonferenza e il diametro

E) la circonferenza e il quadrato del raggio

80. Due triangoli si dicono simili se:

A) la somma delle misure in gradi dei loro angoli interni è 180°

B) gli angoli dell'uno sono uguali a quelli dell'altro

C) hanno un angolo comune

D) hanno un lato comune

E) hanno entrambi un angolo retto

81. In un parallelogramma ciascuna delle diagonali, rispetto al semiperimetro, ha lunghezza:

A) certamente maggiore

B) certamente minore

C) una maggiore, l'altra minore

D) uguale

E) doppia

82. L'angolo che misura 19 p /3 radianti, in gradi sessagesimali misura:

A) 360°

B) 1140°

C) 1170°

D) 1200°

E) 19,9°

83. A quanti radianti corrispondono 180°?

A) p /2

B) 3 p /2

C) 2 p /2

D) 2 p

E) Un numero diverso da quelli delle precedenti risposte

84. In un triangolo, gli angoli a, b e c sono legati dalle relazioni b = a + 20° e c = b + 50°; si ha che c è uguale a:

A) 80°

B) 90°

C) 100°

D) 110°

E) 120°

85. Un palo telegrafico ed un'asta, ad esso parallela e infissa al suolo, proiettano ombre di lunghezze rispettive 3 m e 50 cm. La parte d'asta emergente dal suolo ha lunghezza 2 m. La parte emergente del palo telegrafico, espressa in metri, ha misura:

A) 24

B) 12

C) 3

D) 4/5

E) nessuno dei numeri delle risposte precedenti

86. Il lato di un quadrato è uguale al diametro di una circonferenza (o cerchio). Il rapporto tra la misura della diagonale del quadrato e quella della lunghezza della circonferenza è:

A) maggiore di p

B) uguale a p

C) minore di 1

D) uguale ad 1

E) compreso tra 1 e p , estremi esclusi

87. Sia ABCD un quadrilatero; quale tra le seguenti affermazioni è sempre VERA?

A) ABCD può essere un rettangolo

B) ABCD è un rettangolo

C) ABCD ha due lati uguali

D) ABCD è un trapezio

E) ABCD non può essere un rombo

88. Nel piano cartesiano l'equazione x = -3 rappresenta:

A) una retta giacente nel primo e nel secondo quadrante

B) una retta giacente nel terzo e nel quarto quadrante

C) una retta parallela all'asse delle y

D) una retta uscente dall'origine

E) una retta parallela all'asse delle x

89. La retta y = k + x passa per l'origine degli assi?

A) Sì, sempre

B) Solo per valori negativi di k

C) Solo per k = 0

D) Mai

E) Solo per k > 0

90. In un triangolo rettangolo gli angoli non retti sono:

A) uguali (o congruenti)

B) complementari

C) supplementari

D) ottusi

E) uno ottuso e uno acuto

91. Qual è il volume di una sfera di diametro unitario?

A) p 3

B) p /6

C) 4/3 p 3

D) 4/3 p

E) p 2

92. Due coni retti, a base circolare e di uguale altezza h hanno raggi di base r e s, con r = 0,5 . s. In quale rapporto stanno i volumi rispettivi V (del cono con raggio di base r) e W (del cono con raggio di base s)?

A) V/W = 1/4

B) V/W = 1/3

C) V/W = 1/2

D) V/W = 1/3 . 1/2

E) V/W = 1/ p

93. Quali dei tre triangoli w, z, t rappresentati in figura sono simili?

A) w, z

B) w, t

C) z, t

D) w, z, t

E) Non ci sono figure simili

94. Se la misura, in metri, del diametro di un cerchio è 10^-2, la misura del suo raggio, in metri, è:

A) 1/20

B) 1/200

C) 5^-2

D) 2/10²

E) 2/10

95. Un rombo ha i lati di lunghezza 5 m e un angolo di 30 gradi. La sua area, in m2, ha misura:

A) 0,045

B) 6,25

C) 25

D) 12,5

E) 5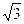 /2

96. Il diametro di una sfera ha lunghezza 6 cm; approssimativamente, il volume della sfera è:

A) 113 cm

B) 113 cm2

C) 113 cm3

D) 904 cm3

E) 904 cm2

97. Quali sono le coordinate dei punti di intersezione dell'asse y con la curva di equazione 4y2 = 2x + 1?

A) (0,1/2) (0,-1/2)

B) (2,0) (-2,0)

C) (2,0) (0,-2)

D) (0,2) (-2,0)

E) (0,2) (0,2)

98. L'equazione della retta passante per i punti (0,0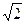) e () è:

A) y = 4x + 1

B) y = 1/4x - 1

C) y = 4x

D) y = 1/4x

E) y = 0,4x

99. Un triangolo, un quadrato, un pentagono e un cerchio hanno perimetro uguale: che cosa si può dire delle loro aree?

A) Il quadrato ha quella massima

B) Il triangolo ha quella massima

C) Il cerchio ha quella massima

D) Il pentagono ha quella massima

E) Sono tutte eguali

100. Quale dei seguenti angoli è acuto?

A) Un angolo di 90°

B) Un angolo di due radianti

C) Un angolo di 300°

D) Un angolo di 370°

E) Nessuno degli angoli menzionati

101. Un triangolo rettangolo ha un cateto lungo 4 e area 8. Il quadrato dell'ipotenusa è pari a:

A) 8

B) 17

C) 20

D) 32

E) 64

102. Una retta inclinata di 45° rispetto all'asse x incontra l'asse y nel punto di coordinate (0, -3). L'equazione della retta è:

A) y = -x + 3

B) y = -x - 3

C) y = x - 3

D) y = x + 3

E) y = -3x + 1

103. Data la parabola di equazione y = x² - 2x, la retta tangente ad essa nel punto (0, 0) è:

A) y = 2

B) y = x + 2

C) y = 2x

D) y = -2x

E) y = x - 2

104. Data la funzione: y = (3/2) . x il diagramma di tale funzione è:

A) la retta generica che passa per l'origine

B) la retta che congiunge l'origine degli assi con il punto P (2,3)

C) una circonferenza di raggio 3/2

D) la retta che congiunge l'origine degli assi con il punto P (- 3,2)

E) una circonferenza di raggio 2/3

105. L'equazione (x²/a²) - (y²/a²) = 1 rappresenta:

A) l'equazione di un'iperbole equilatera

B) l'equazione di una circonferenza

C) l'equazione dell'ellisse

D) l'equazione non ha senso

E) nessuna delle altre risposte è corretta

106. Dato un cubo di volume Vc ed una sfera di volume Vs (diametro sfera = lato del cubo), calcolare il rapporto (Vc - Vs)/Vc:

A) 1 - p /6

B) 1 - p /2

C) p /6

D) p /3

E) p /2

107. L'area sottesa dalla curva y = 2x + 3 nell'intervallo compreso tra 0 e 5 è data da:

A) 2

B) 5

C) 17

D) 24

E) 40

108. Un rettangolo mantiene la stessa area se si aumenta la base di 8 cm e si diminuisce l'altezza di 5 cm. La sua area però, se si diminuisce la base di 5 cm e si aumenta l'altezza di 8 cm aumenta di 130 cm². I lati sono:

A) Base = 30 cm; altezza = 40 cm

B) Base = 35 cm; altezza = 45 cm

C) Base = 40 cm; altezza = 30 cm

D) Base = 50 cm; altezza = 20 cm

E) Base = 60 cm; altezza = 30 cm

109. Sia data la retta y = 2x + b. Perché la retta passi per il punto (1,3) è necessario che b assuma il valore:

A) 3

B) 3/2

C) 6

D) 2/3

E) 10 . 10-1

110. Se si vuole che la parabola y = ax² + bx + c sia simmetrica rispetto all'asse y ad abbia il vertice a quota h, è necessario che:

A) c = 0; b = h/a

B) c = 0; b = -h/a

C) b = 0; c = -h

D) a = 1; c = -h

E) b = 0; c = h

111. Un triangolo con due angoli uguali è:

A) equilatero

B) isoscele

C) rettangolo

D) equiangolo

E) scaleno

112. Un triangolo isoscele, che abbia due lati uguali a 2 cm e l'area uguale a 2 cm²:

A) è inscritto in un cerchio di raggio uguale a 2

B) è anche equilatero

C) ha il terzo lato uguale ad un cm

D) non può esistere

E) è anche rettangolo

113. Due rette distinte sono parallele se, oltre a non avere punti comuni, soddisfano la condizione di:

A) essere omogenee

B) avere la stessa lunghezza

C) formare un angolo di 90°

D) essere complanari

E) non essere complanari

114. Una retta y = ax + b passa per i punti di coordinata (1, 0) e (0, -1). Quale condizione è vera?

A) a > 0 b > 0

B) a < 0 b > 0

C) a < 0 b < 0

D) a > 0 b < 0

E) Nessuna delle precedenti risposte

115. Trovare il valore dell'angolo che è complementare a 169° 41' 11":

A) 10° 18' 49"

B) 11° 15' 24"

C) 17° 14' 39"

D) 79° 41' 11"

E) non esiste

116. Il luogo geometrico dei punti del piano per i quali è costante la somma delle loro distanze da due punti fissi detti fuochi è:

A) la parabola

B) l'iperbole

C) l'ellisse

D) un fascio di rette

E) la circonferenza

117. Il punto in cui si incontrano i tre assi di un triangolo si chiama:

A) metacentro

B) baricentro

C) ortocentro

D) circocentro

E) incentro

118. Dati un pentagono regolare, un quadrato e un triangolo equilatero, tutti di lato A, quale relazione risulta VERA?

A) Area pentagono > area quadrato > area triangolo

B) Area pentagono < area triangolo < area quadrato

C) Area triangolo < area pentagono < area quadrato

D) Area triangolo > area quadrato > area pentagono

E) Area quadrato > area pentagono > area triangolo

119. Data una sfera di raggio R ed un cubo di lato L (con R = L), il rapporto fra le superfici è:

A) 2 p /3

B) 4 p /3

C) 2 p

D) 4/ p

E) 2/3 p

120. Un cono retto ha il raggio di base di cm 6,5 e l'altezza di dm 0,93. Il volume è dato da:

A) 0,617205 dm³

B) 0,4114701 dm³

C) 400,4554 cm³

D) 41,1470098 cm³

E) 1,234410 dm³

121. Sulle superfici di un cubo e di una sfera di uguale volume si può dire che:

A) sono tra loro uguali

B) la superficie del cubo è minore di quella della sfera

C) la superficie del cubo è maggiore di quella della sfera

D) non sono confrontabili tra loro

E) per rispondere bisogna conoscere il valore del volume

122. Fra tutti i triangoli rettangoli con ipotenusa 10 m, il triangolo rettangolo di area massima è quello i cui cateti misurano:

A) 6 m; 8 m

B) 5 m; 5 m

C) 10 m; 10 m

D) 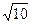m

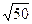E) m

123. Un triangolo rettangolo, ruotando intorno all'ipotenusa, genera:

A) due coni uniti per la base

B) un prisma

C) un tronco di cono

D) un cono retto

E) una piramide

124. La retta di equazione y = 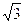x + 45 con l'asse y forma un angolo di ...

A) 30°

B) 45°

C) 60°

D) p /8 rad

E) p /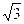 rad

125. Mezzo chilometro quadrato equivale a metri quadrati:

A) 500

B) 5000

C) 50.000

D) 100.000

E) 500.000

126. Sia y = 1 - 4x l'equazione di una retta. Quale, tra le seguenti è perpendicolare alla retta data:

A) y = 1 - 4x

B) y = -1 + 4x

C) y = 2 - 0,25x

D) y = 6 + 0,25x

E) y = 6 + 4x

127. Due quadrilateri si dicono equivalenti quando:

A) hanno uguale perimetro

B) hanno uguale area

C) hanno uguale forma

D) sono sovrapponibili

E) hanno ugual numero di lati

128. All'interno di un cerchio (diametro D) è inscritto un quadrato (lato L) i cui vertici sono quindi sulla circonferenza limite del cerchio. Stabilire quale relazione lega D e L:

A) D = 2L

B) D = 2 . 21/2 L

C) D = 21/2 L

D) D = 3,1416 L

E) D = L²

129. Secondo la geometria euclidea, nello spazio, due rette non parallele:

A) devono sempre incontrarsi in un punto

B) non possono incontrarsi

C) possono non incontrarsi

D) sono sempre coincidenti

E) si incontrano solo se giacciono in piani diversi

130. Quando le due diagonali di un parallelogramma sono perpendicolari fra loro, il parallelogramma è sempre:

A) un rettangolo

B) un trapezio

C) un rombo

D) è un caso impossibile

E) un quadrato

131. L'ascissa del punto di intersezione delle rette y = 3,5 x + 7; y = 0,5x + 5 è:

A) 3

B) 4

C) -3

D) -4

E) -2/3

132. Quale fra le seguenti misure approssima meglio il raggio di una sfera avente volume di 1 dm³?

A) 1 cm

B) 3 cm

C) 6 cm

D) 1 dm

E) 2 dm

133. Un cubo ha il volume di 10^-15 mm³. Il suo lato è:

A) 10^-5 mm

B) 10^-5 cm

C) 10^-3 mm

D) 10^-2 cm

E) 10^-12 mm

134. Data una circonferenza di raggio r, si definisce diametro:

A) il luogo dei punti equidistanti dal centro

B) ogni corda a distanza r/2 dal centro

C) ogni corda passante per il centro

D) il segmento che unisce una qualsiasi coppia di suoi punti

E) ogni semicorda

135. Un cono ha la base circolare iscritta nella base quadrata di una piramide e i due solidi hanno la stessa altezza, h. Qual è il rapporto tra il volume del cono e quello della piramide?

A) p /12

B) 4/ p . h²

C) p

D) p /4

E) p /2

136. Dati tre segmenti di lunghezza 3m, 4m, 5m, dire quale delle seguenti affermazione è VERA:

A) non si può costruire un triangolo

B) non si può costruire un triangolo rettangolo

C) si può costruire un triangolo rettangolo

D) si può costruire un triangolo ottusangolo

E) si può costruire solo un triangolo isoscele

137. Dato un cilindro retto a base circolare di raggio R e altezza h = 2R, qual è il rapporto fra il suo volume e quello della sfera massima contenibile?

A) 3/2

B) 4/3

C) 6/ p

D) p /2

E) p . 3

138. La somma di 2 vettori di modulo v è uguale a un vettore di modulo ancora v. I due vettori formano un angolo pari a:

A) p

B) p /2

C) p /3

D) p /4

E) 2 p /3

129. Quale delle seguenti implicazioni è FALSA?

A) Se il quadrilatero q è un rettangolo, allora le sue diagonali sono uguali

B) Se le diagonali di un quadrilatero q sono uguali, allora il quadrilatero è un rettangolo

C) Se il quadrilatero q è un rombo, allora le sue diagonali sono perpendicolari

D) Se le diagonali di un rombo q sono uguali, allora il rombo è un quadrato

E) Se il quadrilatero q è un quadrato, allora le sue diagonali sono uguali e perpendicolari

130. Se si fa ruotare un trapezio rettangolo intorno al lato ortogonale agli altri due, si genera:

A) un tronco di piramide

B) un tronco di cono

C) un solido costituito da due coni uniti per la base

D) un cono

E) una piramide

131. In un piano cartesiano due cerchi con raggio uguale di lunghezza 5 e centri di coordinate (2; 2) e (10; 8) hanno:

A) infiniti punti in comune

B) due punti in comune

C) un punto in comune

D) nessun punto in comune

E) tre punti in comune

132. La conica y = -3x² + 5:

A) non interseca l'asse x

B) è una iperbole

C) è una ellisse

D) ha un asse di simmetria orizzontale

E) ha un asse di simmetria verticale

133. Un rettangolo ha i lati 10^-3 cm e 10^-2 dm: la sua area è:

A) 10^-2 mm²

B) 10^-4 cm²

C) 10^-5cm²

D) 10^-10 m²

E) 10^-5 dm³

134. Quale delle seguenti rette ha pendenza 60°?

A) y = 0,5 . x +

B) y = 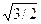x + 1

C) y =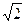

D) y = 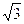x - 1

E) y = x + 2

135. Dette rispettivamente A e B le aree del cerchio inscritto e del cerchio circoscritto ad un quadrato di lato 26 cm, il rapporto B/A vale:

A) 2

B) 0,5

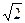
D) 26

E) 2 p

136. La superficie di una sfera di raggio R è:

A) quattro volte l'area del cerchio di raggio R

B) un terzo del volume della sfera

C) il volume della sfera diviso il quadrato dell'area del cerchio di raggio R

D) 4/3 il perimetro della circonferenza di raggio R

E) due volte l'area del cerchio di raggio R

137. La somma di due lati di un rettangolo è 110 cm, la loro differenza 10 cm. Il lato minore misura cm:

A) 20

B) 30

C) 60

D) 50

E) 27,5

138. Un mm³ di sangue contiene circa 5 milioni di globuli rossi (eritrociti). Un individuo adulto ha circa 5 litri di sangue. Il numero di globuli rossi di quell'individuo ammonta a:

A) 25 . 10⁹

B) 2,5 . 10¹²

C) 2,5 . 10¹⁵

D) 2,5 . 10¹³

E) 25 . 10¹³

139. L'equazione y = a/x rappresenta un'iperbole equilatera. Quale deve essere il valore di a affinché l'iperbole passi per il punto P = (3,2):

A) a = 1.5

B) a = 2

C) a = 3

D) a = 6

E) a = 1/6

140. Trovare l'area del triangolo compreso fra gli assi cartesiani e la retta di equazione y = 5 - x/2

A) 5/4

B) 2/5

C) 50

D) 25

E) 10

141. Quale delle seguenti rette rappresenta l'andamento meno decrescente?

A) y = -1/4 x

B) y = -1/2 x

C) y = -x

D) y = -2x

E) y = -4x

142. Quanti spigoli ha un ottaedro regolare:

A) otto

B) dodici

C) sedici

D) venti

E) sei

143. Le equazioni y = x + 1 e y = x + 3 rappresentano:

A) due rette che si intersecano nel punto (1,3)

B) due rette che si intersecano nell'origine

C) due rette perpendicolari

D) due rette parallele

E) due rette che si intersecano nel punto (3,1)

144. Prendendo la terza parte di un angolo retto si ottiene:

A) p /3 rad

B) p /6 rad

C) 60°

D) 20°

E) 30 rad

145. Un cilindro C₁ ha raggio di base K e altezza 2K; un secondo cilindro C₂ha raggio di base 2K e altezza K (con K > 1). Allora:

A) C₁e C₂ hanno lo stesso volume

B) C₁ha volume maggiore di C₂

C) C₂ ha volume maggiore di C₁

D) la risposta dipende dal valore di K

E) il volume è lo stesso solo se K = 1

146. Le due rette y = 2 e y = -3 . x + 2 si incontrano per x = :

A) 0

B) -3

C) 2

D) -2

E) -2/3

147. Nel cerchio il rapporto fra area e circonferenza è:

A) costante

B) irrazionale

C) crescente col raggio

D) r

E) 2/r

148. Per un triangolo rettangolo, quali delle seguenti affermazioni è FALSA?

A) Può essere scaleno

B) Può essere isoscele

C) Può essere equilatero

D) Vale il teorema di Pitagora

E) La somma degli angoli interni è 180°

149. Le seguenti coppie di valori (0, -2) (-3, -5) (1, -1) rappresentano punti di:

A) una parabola

B) un cerchio

C) una retta

D) un ellisse

E) nessuna di queste funzioni

150. Una sfera R ha raggio mille volte più piccolo rispetto a quello di una sfera S. Il volume della sfera S, rispetto a quello della sfera R è:

A) mille volte più piccolo

B) mille volte più grande

C) un miliardo di volte più grande

D) un milione di volte più grande

E) per rispondere bisogna conoscere i valori dei raggi delle due sfere

151. Se il sistema di secondo grado formato dall'equazione di una circonferenza e dall'equazione di una retta non ammette soluzioni reali, significa che:

A) la retta è tangente alla circonferenza nell'origine degli assi

B) la retta interseca la circonferenza

C) la retta contiene il diametro parallelo all'asse delle ascisse

D) la retta non ha punti in comune con la circonferenza

E) la retta sicuramente non giace nello stesso piano della circonferenza

152. In un piano cartesiano, quale delle seguenti equazioni descrive una circonferenza?

A) y + x = r

B) y =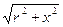

C) x² + y² = r²

D) (x + y)² = r²

E) x² - y² = r²

153. Per tre punti non allineati:

A) passano due circonferenze

B) passano tre circonferenze

C) passano infinite circonferenze

D) passa una sola circonferenza

E) non passano circonferenze

154. Se l'area di un quadrato inscritto in un cerchio vale A, l'area del cerchio è:

A) A . p

B) A . p . 2

C) A . p /2

D) A . 2

E) A/2

155. Quante diagonali distinte possono essere tracciate in un poligono regolare di n lati?

A) n² - 2n

B) (n²/2) - n

C) (n² - 3n)/2

D) n² - n

E) 2n

156. Tra le terne di numeri seguenti, la sola che possa rappresentare le lunghezze dei lati di un triangolo è:

A) 2, 4 ,7

B) 1, 3, 6

C) 1, 2, 4

D) 2, 4, 5

E) 10, 20, 31

157. Siano y = mx + k; y' = m' x + k' due rette del piano. Quale relazione deve sussistere affinché esse siano perpendicolari?

A) m = m'

B) k = k'

C) m = - 1/m'

D) m = 1/m'

E) m < m'

158. L'angolo di 120° è:

A) acuto

B) retto

C) ottuso

D) piatto

E) giro

159. Sia m un numero reale. In un piano cartesiano ortogonale, l'equazione y = mx, al variare di m nell'intervallo (-infinito, +infinito), descrive:

A) tutte le rette del piano

B) tutte le rette del piano passanti per l'origine

C) tutte le rette del piano passanti per l'origine, ad eccezione dell'asse delle ascisse

D) tutte le rette del piano passanti per l'origine, ad eccezione dell'asse delle ordinate

E) solo l'asse delle ordinate

160. Il segmento individuato da due punti di coordinate cartesiane pari a (2, 4) per il primo punto e (-2, 1) per il secondo punto, ha lunghezza eguale a:

A) 3

B) 4

C) 5

D) 16

E) 8

161. Tra le seguenti funzioni

(A) x(1 - x) + 2y = 2 - x²;

(B) - x + 1/2y = 3;

(D) x/3 - y = 2

quali rappresentano due rette tra loro perpendicolari?

A) C e D

B) A e B

C) A e D

D) B e C

E) A e C

162. La distanza fra il punto (1,2) e la retta y = -x è:

A) 1

B) 0

C) 3(1/2)

D) 2(1/2)

E) 3

163. Consideriamo nello spazio una terna di rette cartesiane ortogonali (ciascuna perpendicolare al piano delle altre due e aventi un punto comune detto origine). Se consideriamo su ciascuna retta il punto distante D dall'origine come vertice di uno stesso triangolo, l'area di quest'ultimo è data da:

A) D²

B) D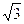

C) (D²)/2

D) (D²/4

E) D

164. La somma degli angoli interni di un poligono è 360°. Si può affermare che il poligono è certamente:

A) un quadrato

B) un rettangolo

C) un pentagono

D) un parallelogramma

E) un quadrilatero

165. Due angoli con i lati reciprocamente perpendicolari risultano essere:

A) uguali

B) supplementari

C) complementari

D) necessariamente retti

E) la risposta dipende dall'ampiezza degli angoli

166. Quale tra i seguenti punti del piano cartesiano è interno alla circonferenza di equazione x² + y² = 30?

A) (6, -3)

B) (5, -4)

C) (5, 2)

D) (4, 4)

E) (-4, 4)

167. In un triangolo rettangolo:

A) ci sono sempre due lati uguali

B) la somma dei quadrati dei due lati minori è uguale al quadrato del lato maggiore

C) i tre lati sono sempre uguali

D) la somma degli angoli non retti è uguale a 180°

E) possono esistere due angoli di 90°

168. La somma degli angoli interni di un esagono non regolare:

A) è pari a 720°

B) è pari a 600°

C) dipende dalla lunghezza dei lati

D) dipende dalla forma del poligono

E) è pari a 1080°

169. Quando un natante percorre un miglio nautico, l'angolo descritto al centro della Terra è 0° 1' 0". In radianti tale angolo è:

A) 1/60

B) p /180

C) 60/ p

D) p /(3 . 60 . 60)

E) p /360

170. (x²/a²) + ( y²/b²) = 1 è l'equazione:

A) di una cicloide

B) di un'iperbole riferita ai suoi assi

C) di un'ellisse riferita ai suoi assi di lunghezza 2a e 2b

D) di una retta passante per due punti a e b

E) di una circonferenza avente per centro il punto P (a, b)

171. L'unità di misura di un angolo in radianti è:

A) gradi sessagesimali

B) gradi centigradi

C) gradi centesimali

D) centimetri

E) nessuna delle precedenti: si tratta di un numero puro

172. In un poligono convesso che ha 54 diagonali il numero dei lati è:

A) 15

B) 12

C) 9

D) 6

E) 27

173. Un triangolo rettangolo ha l'ipotenusa uguale a 25 cm; i suoi cateti misurano:

A) 14 cm e 15 cm

B) 7 cm e 20 cm

C) 5 cm e 25 cm

D) 15 cm e 20 cm

E) 9 cm e 16 cm

174. Se B è la base maggiore, b è la base minore ed h l'altezza, l'area del trapezio è:

A) (B + b) h

B) B . b . h

C) B . b/h

D) (B + b) h/2

E) (B + b) /2h

175. Data la funzione y = 2 . (x + 3) questa è rappresentabile in un sistema di assi cartesiani ortogonali da:

A) una retta in cui y cresce con x

B) un'iperbole in cui y cresce con x

C) una retta in cui y decresce con x

D) una parabola che interseca l'asse delle ordinate in y = 3

E) una retta che interseca l'asse delle ordinate in y = - 3

176. Sono date due sfere di raggi rispettivamente R1, R2 e superfici S1, S2. Se R1/R2 = 4 allora S1/S2:

A) 2

B) 4

C) 8

D) 16

E) 64

177. Un litro di liquido equivale a:

A) un miliardo di millimetri cubi

B) un milione di centimetri cubi

C) centomila microlitri

D) un millesimo di metro cubo

E) l'equivalenza dipende dal tipo di liquido considerato

178. Il rapporto fra i lati omologhi di due triangoli simili è 0,5. Quale è il rapporto fra le loro aree?

A) 0,5

B) 0,25

C) 0,125

D) 0,5 .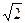

E) 0,5 .

179. Un triangolo è rettangolo e isoscele. Quanto vale un suo angolo acuto?

A) 150°

B) 20°

C) 30°

D) 45°

E) 60°

180. I criteri di uguaglianza dei triangoli:

A) sono due

B) sono tre

C) sono quattro

D) non esistono

E) sono due solo per i triangoli equilateri

181. La diagonale e il lato di un quadrato sono due grandezze il cui rapporto è uguale a:

A) 2

B) 1,414

C) p

D) un numero immaginario

E) uno diviso 1,414

182. La misura di un angolo si effettua con unità espresse in:

A) metri

B) secondi

C) grammi

D) radianti

E) metri quadrati

183. L'equazione y = ax² + bx + c rappresenta una parabola con la concavità rivolta verso il basso se:

A) b = 0

B) a > 0

C) a < 0

D) b < 0

E) a = 0

184. Quale delle seguenti situazioni è impossibile in geometria?

A) Una retta e una circonferenza con un solo punto in comune

B) Una retta e una circonferenza con due soli punti in comune

C) Una retta e un cerchio con un solo punto in comune

D) Una retta e un cerchio con due soli punti in comune

E) Una retta e un cerchio con infiniti punti in comune

185. Dieci litri sono pari a m³:

A) 0,1

B) 1

C) 10^-2

D) 10²

E) 10³

186. Quali dei seguenti punti NON giace sulla retta di equazione y = 2x + 1?

A) (1,3)

B) (0,1)

C) (-1,-1)

D) (3,7)

E) (0,0)

187. A ogni triangolo può essere circoscritta una circonferenza?

A) No

B) Sì, se il centro della circonferenza è l'incentro

C) L'affermazione non ha senso se non si precisa il tipo di triangolo

D) Sì, e il centro della circonferenza è il circocentro

E) Dipende dal perimetro del triangolo

188. I punti di coordinate (3; 4), (6; 8), (9; 12) sono:

A) punti di una retta

B) vertici di un triangolo rettangolo

C) vertici di un triangolo isoscele

D) equidistanti dall'origine degli assi cartesiani

E) punti di una circonferenza

189. Due rette dello spazio sono sghembe se:

A) sono incidenti

B) sono complanari

C) sono parallele

D) non sono complanari

E) sono complanari, ma non sono parallele

190. Se i tre angoli di un triangolo sono eguali ai tre angoli di un secondo triangolo, i due triangoli sono:

A) entrambi equilateri

B) sempre simili

C) sempre uguali

D) entrambi rettangoli

E) non è possibile rispondere perché mancano i valori delle ampiezze degli angoli

191. L'espressione di un angolo in radianti:

A) è numericamente maggiore della corrispondente espressione in gradi

B) non esiste

C) è numericamente uguale alla corrispondente espressione in gradi

D) è proporzionalmente inferiore alla corrispondente espressione in gradi

E) è proporzionalmente superiore alla corrispondente espressione in gradi

192. Qual è il massimo numero di angoli ottusi che possono essere presenti in un triangolo?

A) 1

B) 2

C) 3

D) 0

E) non si può stabilire

193. Il coefficiente angolare di una retta passante per l'origine e tangente alla circonferenza di equazione (y - 2)² + (x - 2)² = 4 è:

A) 0

B) 2

C) -1

D) 1

E) inesistente

194. Quale delle seguenti terne di numeri dà le lunghezze dei lati di un triangolo rettangolo?

A) 2, 2, 2

B) 3, 4, 5

C) 2, 12, 5

D) 7, 7, 11

E) 4, 8, 12

195. L'angolo di 45° è:

A) ottuso

B) acuto

C) piatto

D) retto

E) giro

196. Due rette che giacciono nello stesso piano:

A) sono parallele

B) non si incontrano mai

C) possono essere parallele

D) individuano due piani perpendicolari

E) si incontrano formando sempre un angolo retto

197. Consideriamo un segmento AB di lunghezza L = 21 e il suo asse. Da un punto P dell'asse, a distanza x dal segmento, tracciamo i segmenti PA e PB. Il triangolo PAB è isoscele quando:

A) x = 1

B) x =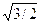

C) x = 21

D) sempre

E) x =

198. La misura della lunghezza x del segmento AB, in centimetri, è:

A) 6 < x < 7

B) 7 < x < 8

C) 8 < x < 9

D) 9 < x < 10

E) 10 < x < 11

199. Una circonferenza è il luogo:

A) dei punti dello spazio equidistanti da un centro C

B) dei punti del piano equidistanti da un centro C

C) dei punti equidistanti da un segmento

D) dei punti equidistanti da due fuochi F1 ed F2

E) dei punti del piano tali che la somma delle distanze dai fuochi F1 ed F2 sia costante

200. Il coefficiente angolare di una retta è:

A) l' angolo formato dalla retta con l'asse delle ascisse espresso in radianti

B) l'angolo formato dalla retta con l'asse delle ordinate espresso in radianti

C) il seno dell'angolo formato dalla retta con l'asse delle ascisse

D) la tangente dell'angolo formato dalla retta con l'asse delle ascisse

E) il coseno dell'angolo formato dalla retta con l'asse delle ascisse

201. L'area di un cerchio vale 300 m2. Indicare quale delle misure sotto indicate dà con approssimazione il raggio di tale cerchio:

A) 20 m (circa)

B) 100 m (circa)

C) 31,4 m (circa)

D) 10 m (circa)

E) 3 m (circa)

202. La rappresentazione grafica nel piano cartesiano della relazione xy = k (con k costante) è una:

A) retta

B) circonferenza

C) iperbole

D) parabola

E) sinusoide

203. Due rette di equazioni y = mx e y = nx sono tra loro sempre perpendicolari se:

A) mn = - 1

B) mn = 1

C) m = n

D) mn = 0,5

E) m/n = 0,5

204. Due triangoli sono sicuramente uguali quando sono uguali:

A) le tre coppie di angoli

B) due lati e l'angolo compreso tra essi

C) due lati e la somma degli angoli interni

D) due lati e l'angolo opposto ad uno di essi

E) un lato e l'angolo opposto ad esso

205. Quale delle seguenti condizioni deve verificarsi affinché la retta di equazione y = mx + n non passi per il quarto quadrante?

A) m > 0, n > 0

B) m < 0, n > 0

C) m > 0, n < 0

D) m < 0, n < 0

E) m > 0, n = 0

206. La somma degli angoli interni di un pentagono non regolare:

A) ha il valore 1080°

B) ha il valore 540°

C) ha il valore 360°

D) il valore dipende dalla lunghezza dei lati

E) il valore è sicuramente inferiore a 540°

207. Due rette che non si incontrano:

A) sono sicuramente parallele

B) giacciono sicuramente in piani diversi

C) giacciono sicuramente nello stesso piano

D) possono essere parallele

E) non sono sicuramente parallele

208. Una retta inclinata di 45° incontra l'asse delle ordinate nel punto di ordinata 3; l'equazione della retta è:

A) y = 3x + 1

B) y = 45x + 3

C) y = x

D) y = x - 3

E) y = x + 3

209. Gli angoli di un triangolo sono in progressione aritmetica, e il maggiore è il doppio del minore; i valori in gradi degli angoli sono:

A) 20, 30, 40

B) 40, 50, 80

C) 60, 90, 120

D) 40, 60, 80

E) 45, 70, 95

210. La terza parte di un angolo retto misura:

A) [pigreco]/3 radianti

B) [pigreco]/6 radianti

C) [pigreco]/2 radianti

D) 45°

E) 60°

211. Se una sfera e un cubo hanno uguale volume, la superficie della sfera è:

A) minore di quella del cubo

B) maggiore di quella del cubo

C) uguale a quella del cubo

D) doppia di quella del cubo

E) i dati forniti non sono sufficienti per rispondere

212. In due triangoli simili, le misure dei lati del più piccolo sono uguali al 50% delle corrispondenti misure del più grande; il rapporto tra l'area del triangolo maggiore e quella del triangolo minore è:

A) 0,25

B) 2

C) 0,5

D) 4

E) i dati forniti non sono sufficienti per rispondere

213. Sia ABCD un quadrilatero; quale delle seguenti affermazioni è sempre VERA?

A) ABCD può essere un rettangolo

B) ABCD è un rettangolo

C) ABCD ha due lati eguali

D) ABCD è un parallelogramma

E) ABCD non può essere un trapezio scaleno

Fonte: http://schiattarella.altervista.org/scuola/TEST/MATEMATICA/geometria.doc

Autore del testo: Carolina Schiattarella

Parola chiave google : Test di geometria tipo file : doc

Test di geometria