Transitori termici
Transitori termici
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Transitori termici
Transitori termici di corpi termicamente sottili
Nella pratica corrente s’incontrano numerosi problemi non stazionari in conseguenza di condizioni al contorno variabili nel tempo. Si pensi, ad esempio, ad un corpo estratto da un forno ed immerso in un bagno di acqua fredda per temprarlo. L’energia si trasferisce per convezione dalla superficie esterna verso il liquido e per conduzione termica dall’interno del corpo verso la superficie. Ne consegue che ogni punto del corpo andrà progressivamente raffreddandosi fino a raggiungere una condizione stazionaria di equilibrio con il bagno.
Per determinare l’andamento della temperatura durante il transitorio termico che precede la stazionarietà si può seguire un approccio valido per i corpi cosiddetti termicamente sottili, ossia corpi che presentano al loro interno gradienti termici talmente piccoli da ritenere la temperatura praticamente uniforme durante l’intero transitorio.
Per stabilire se un corpo può essere considerato termicamente sottile occorre prendere in considerazione un parametro adimensionale chiamato Numero di Biot, abbreviato Bi. Fisicamente esprime il rapporto tra la resistenza conduttiva del corpo e quella convettiva relativa allo scambio con il fluido esterno:
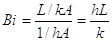
dove L è una grandezza che caratterizza la geometria. Ciò appare evidente nel caso di una lastra piana:
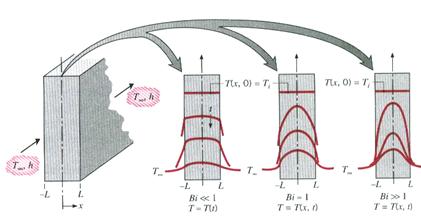
L’evoluzione tra due condizioni di equilibrio termico, quella iniziale e quella finale, si presenta diversa a seconda se Bi<<1 ovvero Bi>>1. Nel primo caso i gradienti interni di temperatura sono modesti rispetto a quelli alle interfacce e viceversa nel secondo caso. Per stabilire dunque la validità dell’ipotesi di corpo termicamente sottile occorre verificare che Bi sia molto piccolo, in pratica Bi<0.1.
L’espressione del numero di Biot può essere generalizzata sostituendo L con una lunghezza caratteristica Lc = V/A, dove V è il volume di materiale e A la superficie esposta al fluido. Nel caso di una lastra piana di spessore 2L, Lc = A2L/2A = L, per una superficie cilindrica Lc = pr2L/2prL = r/2, per una sfera Lc = (4/3)pr3/4pr2 = r/3 e così via.
Trascurando i gradienti termici all’interno del materiale, si può impostare un bilancio globale di energia riferito all’intero volume di materiale in cui l’energia ceduta all’esterno per convezione uguagli la variazione dell’energia immagazzinata, ossia dell’energia interna sensibile in assenza di cambiamenti di stato:

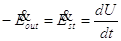
ovvero
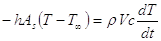
che, riscritta in termini di sovratemperatura 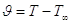 , diviene
, diviene

Separando le variabili e integrando tra t = 0 e t da un lato, e tra 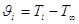 dall’altro, si ottiene:
dall’altro, si ottiene:
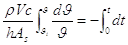
Risolvendo gli integrali:
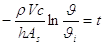
ovvero
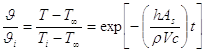
Il termine 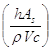 è noto come costante di tempo termica e ha come espressione:
è noto come costante di tempo termica e ha come espressione:
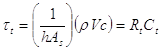
dove  la capacità termica del materiale. Ogni incremento della resistenza termica o della capacità renderà più lento il raffreddamento come mostra la figura:
la capacità termica del materiale. Ogni incremento della resistenza termica o della capacità renderà più lento il raffreddamento come mostra la figura:
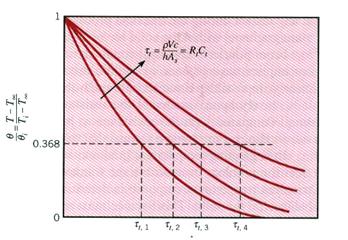
La durata del transitorio è teoricamente infinita; all’atto pratico dopo 4-5 costanti di tempo termiche il corpo si porta alla temperatura ambiente 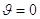 .
.
La quantità di calore ceduta durante il processo, che coincide con la variazione di energia interna del materiale, si ottiene integrando la seguente equazione:
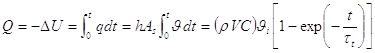
Esempio
La giunzione di una termocoppia, che può essere assimilata ad una sfera, viene utilizzata per misurare la temperatura di una corrente di gas. Si conoscono il coefficiente di convezione h = 400 W/m2K e le proprietà termofisiche della giunzione k = 20 W/mK, c = 400 J/kgK e r = 8500 kg/m3. Calcolare il diametro della giunzione affinché la costante di tempo termica sia pari a 1 s. Se la giunzione si trova a 25°C in una corrente di gas a 200°C, dopo quanto tempo raggiunge 199°C?
Soluzione
Dati:
Le proprietà termofisiche della giunzione
Obiettivo:
- diametro richiesto per avere una costante di tempo di 1 s.
- tempo necessario per raggiungere 199°C
Schema:

Ipotesi semplificative:
- Corpo termicamente sottile
- Scambi radianti trascurabili
- Perdite per conduzione attraverso i cavetti trascurabili
- Proprietà termofisiche costanti
Analisi:
- Poiché non sono note le dimensioni della giunzione non è possibile in questa fase stabilire se il corpo possa essere considerato termicamente sottile. Può essere ragionevole ipotizzare che lo sia e verificare successivamente la validità dell’ipotesi. Dalla relazione di definizione della costante di tempo si può determinare il diametro che è l’unica incognita:
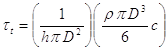
da cui
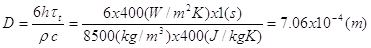
Si calcoli Bi con Lc = D/6:

Il basso valore di Bi rende dunque plausibile l’ipotesi di corpo termicamente sottile.
- dalla relazione
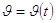 si ottiene:
si ottiene:
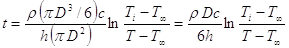
sostituendo i valori numerici:
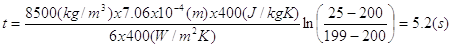
Commenti:
Il tempo richiesto per raggiungere la quasi stazionarietà è di circa 5 volte la costante di tempo termica di 1s.
In presenza di scambi per irraggiamento con i corpi circostanti e per conduzione attraverso i cavetti della termocoppia, la durata del transitorio si modifica e la temperatura di regime differirà da quella della corrente di gas.
Fonte: http://meccanico.weebly.com/uploads/7/7/0/5/770526/transitori.doc
Autore del testo: non indicato nel documento di origine
Parola chiave google : Transitori termici tipo file : doc
Transitori termici
Transitori termici
Lo studio dei transitori termici implica l’analisi di una evoluzione spaziale e temporale della temperatura. Questo tipo di problema richiede, per la sua risoluzione ,strumenti matematici il cui utilizzo risulta essere spesso complicato; sono infatti necessarie le equazioni differenziali, le quali sono raramente risolubili per via analitica. Per ovviare a questo problema si utilizzano tecniche fornite dal calcolo numerico, che seppur non forniscano la soluzione esatta rendono facilmente disponibili soluzioni approssimate che possono essere anche molto accurate.
Prendiamo per esempio una lastra piana ed indefinita di spessore s che per t<0 si trova alla temperatura T=T0 e in seguito al tempo t=0 andremo ad immergere in olio bollente. Operiamo usando il metodo delle differenze finite: discretizziamo lo spessore della lastra suddividendola in una successione di strisce di spessore Dx e abbiamo:
 (1)
(1)
dove:
- s è lo spessore totale della lastra
- Dx è lo spessore di una striscia
- Nd è il numero di suddivisioni in strisce
Rappresentiamo la situazione con il seguente schema:

Figura 1 – Discretizzazione geometrica della piastra

Supponiamo ad esempio di suddividere lo spessore della lastra in 7 strisce e operiamo la suddivisione in modo tale che ogni striscia abbia spessore Dx tranne quelle adiacenti alla pelle della lastra che saranno prese di spessore Dx/2.Individuiamo quindi dei punti particolari che chiameremo nodi prendendo il primo e l’ultimo sulle facce della lastra mentre quelli interni al centro di ciascuna striscia.
Operando in questo modo tutti i nodi sono distanti Dx tra loro e saranno pari al numero di strisce meno una.
I nodi sono punti molto importanti perché approssimiamo la temperatura dell’intera striscia con la temperatura del nodo che contiene, in questo modo possiamo trascurare le variazioni di temperatura che si hanno tra un lato e l’altro di una stessa striscia.
Abbiamo dunque effettuato una discretizzazione spaziale ; l’ascissa x è cioè una variabile discreta e vale la relazione :
 (2)
(2)
dove i è un numero intero non negativo che chiamiamo indice di nodo. (i=0…Nd)
Effettuiamo anche una discretizzazione temporale; per questo dobbiamo prendere un opportuno passo temporale Dt e vale la relazione:
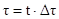 (3)
(3)
dove t è l’indice di tempo.
Per risolvere il transitorio ci serviremo di una matrice bidimensionale di questo tipo:
nodo |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
tempo |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
Figura 2
Per indicare la temperatura di un nodo ad un certo istante temporale useremo la notazione :
 dove l’apice è l’indice di tempo e il pedice è l’indice di nodo.
dove l’apice è l’indice di tempo e il pedice è l’indice di nodo.
Vogliamo ora trovare l’algoritmo che permetta di stimare il profilo delle temperature al passo temporale successivo dalla conoscenza delle temperature di ogni nodo al passo corrente.
Rifacciamo la costruzione dell’equazione di Fourier concentrando la nostra attenzione su un generico nodo a un generico istante di tempo.
Dobbiamo scrivere la variazione di temperatura in funzione dei flussi di calore sulla faccia destra e sinistra usando il principio di conservazione dell’energia:
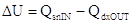 (4)
(4)
dove :
- 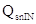 è la quantità di calore entrante dal lato sinistro della striscia
è la quantità di calore entrante dal lato sinistro della striscia
- 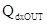 è la quantità di calore uscente dal lato destro della striscia
è la quantità di calore uscente dal lato destro della striscia
D’altra parte sappiamo che :
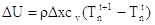
(5)
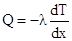
che discretizzando la derivata diventa:
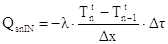 (6)
(6)
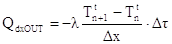 (7)
(7)
Da queste uguaglianze la (4) diventa:
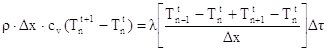 (8)
(8)
avendo ipotizzato 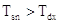
Da questa equazione ricaviamo la temperatura al tempo t+1 e ottengo:
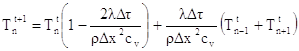 (9)
(9)
Ci poniamo ora il problema di vedere se l’intervallo temporale Dt possa essere preso grande a piacere. Notiamo che se Dt fosse troppo grande il coefficiente che moltiplica 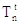 fosse negativo potrebbe anche diminuire contraddicendo il secondo principio della termodinamica.
fosse negativo potrebbe anche diminuire contraddicendo il secondo principio della termodinamica.
Esiste dunque un valore limite di Dt che si ottiene ponendo nullo il coefficiente di 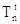 e vale:
e vale:
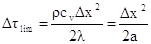 (10)
(10)
essendo
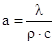
una grandezza che rappresenta la rapidità di propagazione delle variazioni di temperatura nel materiale detta diffusività termica.
In questa tecnica ,detta TIME MARCHING, permette inoltre di simulare una velocità di propagazione del calore
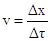
che diminuisce al diminuire di Dx.
Se nella (9) usiamo Dtlim questa diventa:
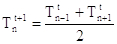 (11)
(11)
che è la media aritmetica tra le temperature dei nodi adiacenti.
Questa scelta di Dt è probabilmente un po’ troppo “grossolana”, infatti per il calcolo di 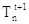 .
.
Si usa scegliere il Dt ottimale che è uguale ai 2/3 del Dt limite.
Con questa scelta la (9) diventa:
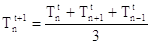 (12)
(12)
Dove a causa di un passo temporale più piccolo devo eseguire un numero maggiore di operazioni ma ottengo una soluzione più accurata.
Fonte: http://pcfarina.eng.unipr.it/dispense00/baruffini125046.doc
Autore del testo: Baruffini
Parola chiave google : Transitori termici tipo file : doc
Transitori termici
Visita la nostra pagina principale
Transitori termici
Termini d' uso e privacy