Cinghie trapezoidali

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Cinghie trapezoidali

Vengono definite cosi in quanto la sezione della cinghia è trapezoidale, viene usata cosi perché migliora il rapporto tra la trazione sulla cinghia e lo sforzo normale per via dell'incuneamento della cinghia.

Se applichiamo uno sforzo normale N si ha che:

in una cinghia piana nasce una forza tangenziale paro a F_r;
in una cinghia trapezoidale corrisponde su ogni superficie di contatto una

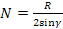
Praticamente è come se il coefficiente di attrito fosse aumentato da f a (f/sin γ), da cui l'uso di queste cinghie. Per entrambe le superfici di contatti si ha che la forza tangenziale totale è data da:

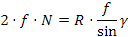
Le cinghie trapezoidali sono costituite essenzialmente di due parti:

un anima resistente alla trazione: si tratta di tante piccole funi disposte longitudinalmente e possono essere in fibra vegetale, sintetica oppure di fili metallici.
un rivestimento di gomma.

Le cinghie si costruiscono ad anello chiuso o aperto, in quelle ad anello chiuso le funi sono in realtà un unica fune che si avvolge varie volte (più funi infatti rischierebbero di essere di diverso diametro e questo porterebbe alcune di loro ad essere sollecitate prima causando una possibile rottura).

In quelle ad anello aperto si ha una giunzione con bulloni, in questo caso l'anima è tessile e costituita da una tela arrotolata, ma questo tipo di anelli è usato poco perché:

la giunzione è un punto debole;
la giunzione è anche fonte di disturbo durante il funzionamento perché provoca una variazione della densi cinghia ed è anche diversa la rigidezza di conseguenza.

Le cinghie sono realizzate con sezione unificate in cui variano le grandezze l₁ e l₂ e hanno tutte in comune l'angolo di 40°. Durante il funzionamento la parte inferiore si allarga e l'angolo diminuisce (~ 36°), tanto più è piccolo il raggio su cui la cinghia si incurva tanto più diminuirà l'angolo quindi per ogni diametro di puleggia c'è un certo angolo di gola (ad es. 34°).

Si ha che la cinghia sollecitata a trazione si deforma con l'incurvarsi sulla puleggia, ecco perché non viene realizzata con forma trapezoidale quando scarica ma in modo tale che assuma una forma trapezia all'essere avvolta attorno alla puleggia.

2. Condizione di accoppiamento tra cinghia e puleggia

Il caso è analogo a quello del freno a mano, possiamo scrivere che:

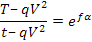
dove:

q è il rapporto fra massa e unità di lunghezza;
α è l'angolo su cui avviene lo scorrimento;
α₀ è l'angolo di avvolgimento.

Come abbiamo detto, in questo caso si ha strisciamento globale fra nastro e tamburo ed è valida l'espressione

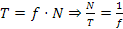Se lo scorrimento non è globale questa uguaglianza è valida solo per freni e frizioni.

In generale nelle trasmissione a cinghia si vuole evitare proprio lo scorrimento globale, tuttavia l'espressione di e ^{f α} rimane valida per via del fatto che il flessibile è estensibile. Questo comporta che all'applicare le forze T e t si applica un momento tale che.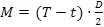

Se t ha un valore stabilito allora possiamo pensare di partire da un valore M=1 (quindi con T=t) e aumentare M e T gradualmente in modo da mantenere l'equilibrio fino a raggiungere il valore limite per cui un ulteriore aumento di M dà luogo allo scorrimento globale. In quel momento si ha che l'espressione è valida perché si è in condizioni di strisciamento per i quali è noto che vale la.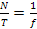

Quindi al limite di slittamento (o scorrimento globale) della puleggia si ha la relazione:

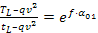dove poniamo.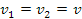

Rimane da capire se la stessa relazione è valida per M < M_lim , sappiamo che esistono le relazioni :

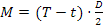
dove α < α₀ e α corrisponde all'angolo dove avviene lo scorrimento locale (cioè dove la puleggia e la cinghia hanno uno scorrimento reciproco).

Quando non si è al limite di scorrimento si può scrivere quindi che:

Si noti che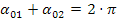, questo è vero solo approssimativamente perché in realtà la velocità dei due rami della cinghia non è la stessa (è maggiore la velocità del ramo teso).

3. La potenza massima trasmissibile

Posti al limite di slittamento della puleggia 1 si ha .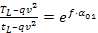

Si ha pero che i calcoli vanno riferiti alla puleggia dove si raggiunge prima il limite di slittamento, che a parità di coefficiente di attrito è quella con angolo di abbraccio inferiore.

Essendo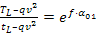e quindi

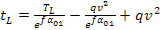La condizione limite di slittamento corrisponde ad una forza periferica limite:

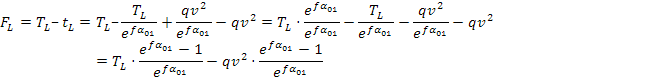
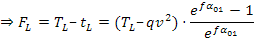
Da questa si può ricavare il momento trasmissibile o direttamente la massima potenza trasmissibile in corrispondenza al limite di slittamento:

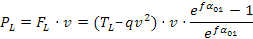
la potenza massima che si può trasmettere è quella per cui T_L assume il massimo valore, questa tensione dipende da f e da α₀₁, se definiamo T_M questo valore massimo allora si ha che dipenderà dalla resistenza della cinghia.

Quindi aumentando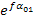aumenta anche T_L e questa può arrivare ad un valore massimo T_M oltre il quale la cinghia si rompe. La potenza massima trasmissibile è quindi pari a:

ovviamente per poter realizzare una trasmissione ci si pone in condizioni da non stare al limite dello scorrimento né al limite di rottura.

4. Il rendimento della trasmissione

Dalla figura vediamo che possiamo scrivere:

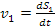
si ha per forza che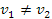 dove dS₀ è lo spostamento nel tempo dt a cinghia scarica.

Vediamo che il tratto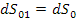 si allunga e diventa dS₂.

I corrispondenti allungamenti sono dati da.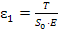

Vediamo che questo diventa funzione delle tensioni, e rappresenta inoltre il rapporto di trasmissione, infatti:

la potenza che la puleggia motrice 1 trasmette alla cinghia è;
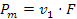la potenza che la cinghia trasmette alla puleggia condotta 2 è.

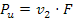In queste espressioni la forza periferica F è la stessa perché è data dalla differenza tra le tensioni, che non varia sia in corrispondenza della puleggia che della condotta.

Il rendimento della trasmissione (che non è il rendimento totale) tiene conto solo delle perdite di potenza dovute al fatto che la cinghia è deformabile, per cui:

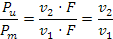
Quindi l'elasticità della cinghia produce una perdita di potenza pari a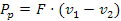, questa perdita si distribuisce tra gli strisciamenti locali sulle due pulegge, provocando un riscaldamento delle parti in contatto. Questo strisciamento però è quella che permette di ricavare il legame tra T, t e α₀.

5. Il legame tra le tensioni

Posti nel caso in cui si è al di sotto del limite di slittamento si rappresenta come in figura l'allungamento della cinghia punto per punto. Sul ramo superiore l'allungamento unitario dovuto a T è ε₁ e su quello inferiore dovuto a t è ε₂.

Puleggia 1

Valutiamo le tensioni lungo l'arco d'avvolgimento misurando α in senso orario come in figura, partendo da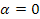ed essendo il flessibile estensibile si ha che ci sono strisciamenti locali della cinghia rispetto alla puleggia per cui si può tornare a scrivere:

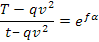
esplicitando T in funzione di α si ha:.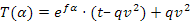

Procedendo lungo l'arco di avvolgimento e aumentando l'angolo di abbraccio α vediamo che anche T(α) aumenta fino al valore finale T del ramo superiore e siccome si è al di sotto del limite di slittamento si ha che questo valore finale viene raggiunto per un valore:

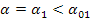Si giunge cosi ad un valore finale T(α₁) per il quale vale ancora la relazione:

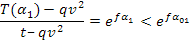
quindi in tutte le condizioni di carico per cui si è al di sotto del limite di slittamento le due tensioni sono legato da una relazione in cui compare l'angolo di abbraccio α₁. Questo deriva dal fatto che da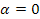l'allungamento ε va uamentando e quindi c'è strisciamento tra puleggia e cinghia, superato α₁ l'allungamento rimane costante e pari a ε₁. Si può scrivere:

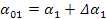
perché per tutto l'arco Δα1 l'aderenza è completa e l'allungamento rimane costante.

Puleggia 2

Si noti che la velocità della puleggia 1 è uguale alla velocità della cinghia nel puntoin cui la velocità della cinghia è massima. Poiché la puleggia 2 è condotta, le velocità saranno uguali quando sara al minimo, infatti la velocità della condotta non sarà mai più veloce della cinghia.

Per arrivare da un valore di tensione T a t serve ruotare di un angolo.

6. Tensione a fermo

Si considerano noti il momento da trasmettere e il diametro della puleggia da cui si calcola F = T- t e si stabilisce T_max. Si deve fare il montaggio con la cinghia tesa in modo tale che durante il funzionamento si stabiliscano i valori di T e di t desiderati.

Quando tutto è fermo non si ha momento e i due tratti di cinghia sono ugualmente tesi (si trascura la gravità per via della forma trapezoidale della cinghia) e valgono le relazioni:

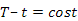
e la tensione t₀ viene stabilita fissando il valore di abbassamento della cinghia al centro tra le due pulegge sotto l'effetto di una forza assegnata.

7. Sollecitazioni sulla cinghia

Nella relazione che fornisce la massima potenza trasmissibile P_max compare la T_M il cui valore è proporzionale alla resistenza della cinghia e serve quindi a capire come viene sollecitata. Sembra, a prima vista, che sia applicata solo una forza di trazione ma questo è il caso ideale, in realtà la cinghia non è inestensibile né completamente flessibile, ha una sua rigidezza e quindi un comportamento sotto carico di tipo elastoplastico.

Quindi per poter essere flessa deve essere applicato un certo momento, per cui si ha:

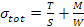
dove J è il momento di inerzia e y la distanza dall'asse neutro.

Questa equazione è valida pero per sezioni omogenee (sono teorie che risalgono a quando le cinghie usate erano piatte), la cinghia trapezoidale non ha sezione omogenea ma la formula può essere ricondotta a una sezione omogenea equivalente.

Si ha nel caso simile di una trave incurvata che:

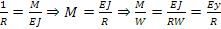Compare il diametro d perché si costringe la cinghia a curvarsi col raggio della puleggia più piccola, nota cosi la tensione ammissibile si ricava anche la tensione ammissibile T_MAX della cinghia reale. Nel caso ideale la cinghia passa da curvatura infinita a curvatura finita con un salto dello sforzo di trazione semplice a uno sforzo di trazione e flessione.

Nel caso reale si nota che il contatto della cinghia sulla puleggia inizia non nel punto dovuto ma un po oltre, questo per via della rigidezza della cinghia in sé ma anche per l'azione centrifuga che tende e gonfiare i due rami della cinghia.

Quindi in realtà la cinghia passa gradualmente da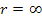, e nel tratto rettilineo si ha solo trazione, dopo il punto B evidenziato in figura si ha trazione e momento flettente (la cinghia inizia a curvare e dal punto di contatto in poi si ha il massimo momento flettente.

8. Velocità di massimo effetto

La velocità di massimo effetto è la velocità per la quale, a parità di altre condizioni, rende massima la potenza trasmissibile.

In precedenza abbiamo visto che: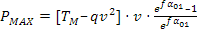, la prima esprime la potenza che può essere trasmessa ad una certa velocità compatibilmente con la resistenza della cinghia e con il limite di slittamento. Dall'espressione di questa potenza si vede che esiste una velocità particolare che rappresenta le condizione ottime per la trasmissione, ovvero di massima potenza trasmessa.

Una volta stabilita la geometria della cinghia e al variare della sola velocità il termine 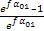. Quest'ultima condizione esprime il fatto che la velocità cresce ad un punto tale che tutta la resistenza della cinghia serve a bilanciare la forza centrifuga.

Vediamo inoltre che la condizione di potenza massima si trova ponendo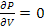e si ottiene:

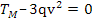
da cui si ricava la velocità di massimo effetto:

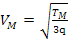sostituendo la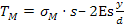si ottiene:

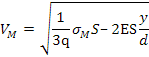
Se teniamo inoltre conto del fatto che la densità lineare di massa q è data da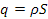si ha:

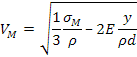
vediamo che non c'è più l'area della sezione, questo significa che per tutte le cinghie con la stessa densità la velocità di massimo effetto è la stessa indipendentemente della grandezza della sezione. Si considera pero la trazione costante lungo la sezione della cinghia, cioè si considera la sollecitazione di tipo statico.

Per cinghia della serie normale risulta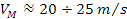, questo non vuol dire che le trasmissioni debbano essere dimensionate seguendo questo requisito ma quanto più la velocità a regime si avvicina a quella di massimo effetto minore sarà il numero di cinghie necessarie a trasmettere la stessa potenza.

La sollecitazione è di fatica per cui i limiti di resistenza che vengono introdotti non sono costanti ma variano col numero totale di cicli di sollecitazione e quindi variano anche con la velocità. In realtà il valore della velocità V_M non è costante ma oscillerà all'interno di un campo di valori a seconda della velocità e della lunghezza della cinghia (fattori che influenzano il numero di cicli).

Quindi per V_M non si ha un valore preciso ma un campo entro cui è bene che cada la velocità di impiego.

9. Progetto della trasmissione

Si ha:

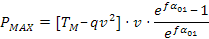
sostituendo in essa l'espressione di TM si ottiene:

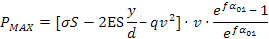
dove compaiono:

la capacità di resistere della cinghia:;
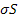la parte di questa capacità impegnata nella flessione:;
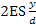la parte di questa capacità impegnata per equilibrare la forza centrifuga;

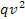quello che rimane dalla differenza di queste parentesi quadre è ciò che viene usato per l'effettiva trasmissione di potenza.

Si consideri una trasmissione definita in tutti i suoi particolari, il termine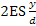a cui ogni zona della cinghia è sottoposta ciclicamente avvolgendosi sulle due pulegge.

La maggiorazione si effettua considerando una sezione S e il tempo che impiega per compiere un giro, nel corso di un singolo giro è sollecitata:

una volta alla trazione massima quando S passa lungo la zona in cui agisce T_M;
una volta alla trazione minima quando passa lungo la zona di t;
due volte alla sollecitazione centrifuga e a flessione quando passa per la periferia delle due ruote;

Mentre il termine della forza centrifuga qv² è uguale per le due ruote (da cui si introduce lo stesso coefficiente di maggiorazione ς) lo stesso non vale per il termine di flessione, nel corso del singolo giro si ha che è pari a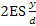per cui occorrerebbero due coefficienti di maggiorazione. Per ovviare al problema si considera una coppia di pulegge equivalenti che abbiano lo stesso diametro d_e compreso tra d e D.

In questo modo si può considerare un unico termine di flessione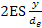al quale sarà applicato un unico coefficiente di maggiorazione ξ che vale per entrambe le ruote.

Il diametro medio equivalente è in sostanza il diametro che a parità di cinghia, velocità e diametro d_e della puleggia dà luogo allo stesso affaticamento effettivo della cinghia per quella determinata trasmissione.

Si ottiene l'espressione della massima potenza trasmissibile:

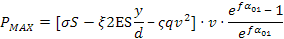
E' opportuno considerare che la trazione σ che compare è in realtà il valore ammissibile di trazione della cinghia che non può essere ritenuto costante ma variabile con la velocità. Dipende infatti dal numero di cicli per ora e si ha che con ogni ciclo si ha per via del moto vermicolare della cinghia che ci sono delle contrazioni e dei rilassamenti locali.

Questa successione alternata di trazioni e rilassamenti provoca un riscaldamento della cinghia che provoca una riduzione di resistenza meccanica (ovviamente in modo proporzionale alla capacità della cinghia di smaltire calore).

A parità di altre condizioni, maggiore è la velocità minore sarà la possibilità di smaltire il calore che può portare ad un danneggiamento della cinghia che diventa più sensibile alla fatica. Si riscrive quindi l'espressione della potenza legando il valore di σ al valore della velocità con un esponente pari a 0,09 (infatti il valore della massima tensione ammissibile varia pochissimo con la velocità).

Si ha:

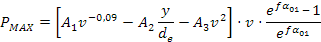
dove A₁, A₂ e A₃ sono coefficienti dimensionali i cui valori sono fissati quando si hanno il tipo di cinghia e la sua sezione, la velocità v e il numero totale di cicli di sollecitazione. Quindi queste tre grandezze sono definite da S, v e L per un determinato tipo di costituzione della cinghia, ovviamente è impossibile effettuare una tabellazione dei valori.

Quindi per ogni trasmissione e cinghia di cui sono noti α₀, d_e, S, v e L si possono trovare i coefficienti A₁, A₂ e A₃ e calcolare il valore di P_MAX trasmissibile al limite di slittamento.

La potenza attuale

É la potenza della trasmissione che deve essere progettata, difatti in condizioni di scorrimento non interessa la potenza massima trasmissibile in condizioni di scorrimento limite ma la potenza massima trasmissibile in condizioni di sicurezza e cioè lontano dallo scorrimento limite, serve applicare quindi all'espressione di P_MAX un coefficiente di sicurezza χ nei confronti dello slittamento:

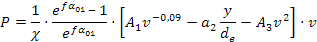
si noti inoltre che in questa espressione la prima parte è adimensionale e il termine fra parentesi quadre rappresenta una sollecitazione (di fatica come abbiamo visto).

La potenza tipo

Fissiamo una trasmissione equivalente o trasmissione tipo come in figura.

Trasmissione di progetto

Trasmissione tipo

Sezione

d,D

→

Sezione

L₀

de ≠ d ≠ D

La trasmissione tipo è data da due pulegge che hanno lo stesso diametro d_e (per cui τ=1) e trasmettono la potenza attraverso la cinghia che ha la lunghezza di riferimento L₀. La velocità della trasmissione tipo è la stessa di quella di progetto e la potenza che trasmettere viene detta trasmissione tipo P0:

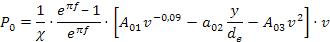
La potenza tipo variazione quindi solo con la velocità, una volta fissata la durata H e il coefficiente di sicurezza periferica lo slittamento χ si ha che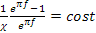 e raggruppando con le altre costanti:

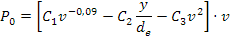
Ovviamente per ogni sezione di cinghia si possono determinare le costanti C_1,2,3 per la corrispondente trasmissione tipo, di solito i costruttori delle cinghie forniscono i tabulati dei valori di queste costanti. E quindi è possibile ricavare la potenza attuale da:

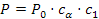
Si ha:

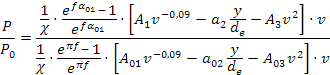
e si ha che:

i χ si semplificano;
d_e è lo stesso per entrambi;

si ha che vengono forniti i valori della potenza tipo in funzione di d_e e della velocità di trasmissione.

Inoltre si ha che il valore di de è dato in funzione del diametro della cinghia reale.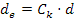

Ricordiamo: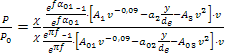

dove:

C_α è un coefficiente che dipende solo da α₀₁ tramite la relazione
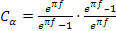
C_L è un coefficiente che dipende dalla diversa lunghezza delle cinghie delle due trasmissioni;

Nel determinare questi coefficienti si fa riferimento sempre al numero di ore stabilite affinché la trasmissione che viene progettata abbia la stessa durata di quella tipo espressa in numero di ore di funzionamento e non in numero di cicli. Nei cataloghi dei produttori si fa riferimento alla durata relativa ovvero al rapporto fra la durata della trasmissione effettiva e quella della trasmissione tipo, cataloghi più recenti riportano el durate in ore che per le trasmissione industriali è dell'ordine delle migliaia di ore.

Protocollo riassuntivo

Stabilita la trasmissione come:

sezione della cinghia (Z, A, B, C, D, E);
diametro delle pulegge (d, D);
lunghezza L;
angolo di avvolgimento α₀₁.

Si calcola la potenza che la cinghia può trasmette si deve calcolare la potenza tipo P₀ usando le tabelle e calcolare poi la potenza attuale da:

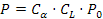
dove:

C_α è tabulata in funzione di α0;
C_L è espressa in funzione della lunghezza commerciale della cinghia.

Fonte: http://raid996.altervista.org/costruzioni.odt

Sito web: http://raid996.altervista.org/

Autore del testo: Raid996

Elaborato da:
Renato Campus Giraldo

Supporto didattico:

Dispense del Prof. Di Francesco

Parola chiave google : Cinghie trapezoidali tipo file : doc

Cinghie trapezoidali