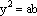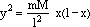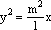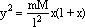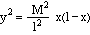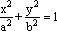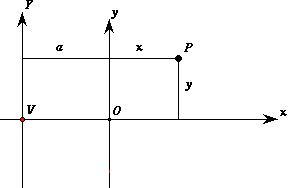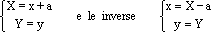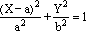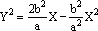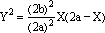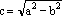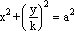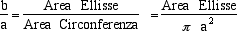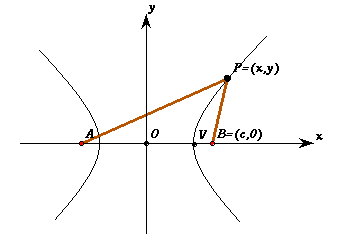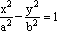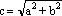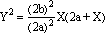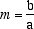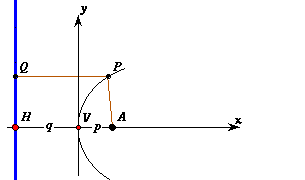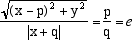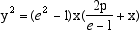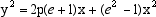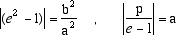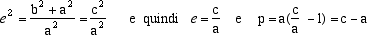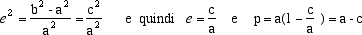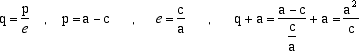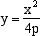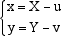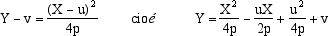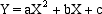Coni circolari e loro sezioni

1. Rappresentazioni prospettiche di una circonferenza

Il problema di trovare una curva piana che, a vederla, susciti la stessa sensazione visiva che suscita la visione di scorcio di una circonferenza e poterla descrivere esattamente come luogo geometrico o in modo quantitativo con delle coordinate, è estremamente interessante dal punto di vista della pittura. Alberti nel Libro II del De pictura, propone due metodi empirici per risolvere il problema, il primo approssimando un cerchio con dei piccoli quadrati (metodo suggerito anche da Piero della Francesca) che poi vengono "scorciati", il secondo usando l'ombra che la luce di una candela proietta sul quadro quando si interponga un disco. Leonardo come vedremo più avanti escogita dei "compassi" in grado di disegnare direttamente i luoghi voluti. Una più dettagliata analisi di come questo problema sia stato affrontato nel rinascimento si trova nella scheda allegata al De pictura sullo scorcio del cerchio.

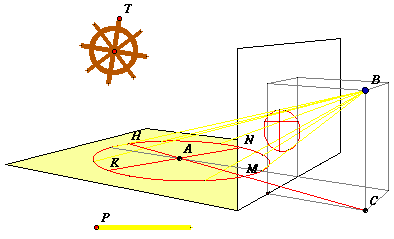
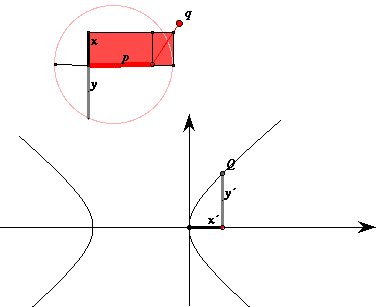
La questione, non semplice, si riduce a quella di trovare una qualche proprietà geometrica che caratterizzi i punti del piano (il quadro) nei quali si proietta la data circonferenza. La curva che si ottiene è una conica e il problema è quello di descriverla a partire dai dati del problema: posizione e raggio della circonferenza, posizione dell'occhio e posizione del piano su cui si proietta. Per rendersi conto della difficoltà del problema basta osservare l'animazione che abbiamo realizzato: lo scorcio della circonferenza dipende in modo essenziale, come prevede il teorema 35 dell'Ottica, dalla proiezione C dell'occhio sul piano del cerchio e dalla retta CA che la congiunge al centro. Possiamo col mouse spostare l'occhio agendo sul punto P allontanandolo dal raggio della circonferenza di base perpendicolare alla linea di terra che pure gioca un ruolo molto importante.

Pascal nel suo trattato sulle sezioni coniche, oggi perduto e del quale ne resta solo una breve trascrizione realizzata da Leibniz, definisce queste curve a partire dalla rappresentazione prospettica di una circonferenza:

È dunque chiaro che se l'occhio è nel vertice del cono e quello che gli si presenta è una circonferenza che è la base del cono e se il quadro è il piano che incontra da una parte e dall'altra la superficie del cono, allora la sezione conica che è generata da questo stesso piano ... che sia ... una ellisse una parabola o una iperbole, sarà l'immagine della circonferenza del cerchio.

La trattazione di Pascal, per quanto è stato possibile agli storici ricostruire, dava la soluzione teorica di come tracciare geometricamente una conica conoscendo solo la posizione di 5 suoi punti, metodo, quello di Pascal, fondato sul suo celebre teorema dell'esagono mistico, uno dei gioielli di tutta la matematica, su cui oggi si basano i metodi della computer grafica che disegnano la conica a partire da 5 punti fissati. L'approccio di Apollonio di Perga (III secolo a.C.) del quale seguiremo l'impostazione è di natura, diremmo aggi, analitica: Apollonio cerca di descrivere la sezione conica come luogo definito da una qualche proprietà geometrica facilmente traducibile in metodi di calcolo (l'algebra oggi, le applicazioni delle aree ieri).

Cominciamo col fissare alcune definizioni base.

Definizione di cono (circolare non degenere).
Data una circonferenza di centro A e un punto V fuori dal piano della circonferenza, si chiama cono (circolare non degenere) l'insieme dei punti appartenenti alle rette che congiungono V coi punti della circonferenza.

La circonferenza è detta base (o generatrice) del cono, il punto V vertice, le rette che lo costituiscono direttrici, la retta AV si chiama asse . Se il punto V appartiene al piano della circonferenza il cono è detto degenere e coincide col piano della circonferenza. I coni che prenderemo in esame, saranno sempre, salvo esplicita menzione, circolari e non degeneri. Osserviamo che abbiamo definito il cono come generato da rette e non da semi-rette il che significa che i nostri coni hanno due "falde" simmetriche rispetto al vertice.
Un cono è retto se l'asse è perpendicolare al piano di base. In questo caso, se E è un punto della base, i segmenti VE sono tutti uguali e i triangoli EVF (EF è un diametro della circonferenza di base) sono tutti isosceli. È questo il primo caso trattato da Euclide e il cono si genera dal movimento di un compasso: l'asse è dato dalla "gamba" fissa e la direttrice dalla "gamba" mobile che traccia la figura. L'angolo di apertura del compasso è fisso e il cono è ottenuto ruotando attorno all'asse la "gamba" con la punta di matita.

Definizione di conica (non degenere) ¹.
L'intersezione di un cono retto con un piano non passante per il suo vertice si chiama conica (non degenere). A seconda di come il piano è messo rispetto alle direttrici abbiamo tre tipi di curve: l'ellisse quando il piano interseca tutte le direttrici, la parabola quando il piano è parallelo a una direttrice, l'iperbole quando è parallelo a due direttrici (quelle che appartengono al piano parallelo al piano dell'iperbole passante per il vertice). È evidente che non possono verificarsi altre possibilità. Se il piano con cui intersechiamo il cono passa per il vertice la conica che si ottiene (detta degenere) si spezza in due rette o in una o in un punto. Salvo esplicita menzione le coniche che considereremo saranno sempre non degeneri.
Nella figura animata seguente possiamo cambiare l'inclinazione del piano secante e realizzare i tre tipi di conica.

Coni circolari e loro sezioni

2. L'impostazione teorica di Apollonio

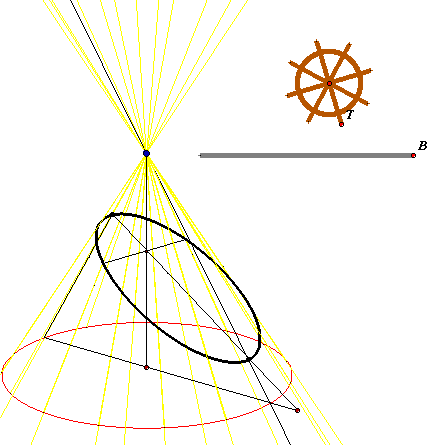
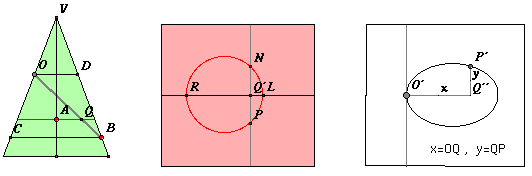
Cerchiamo, in questo paragrafo, di ricostruire le linee essenziali delle idee di Apollonio autore di un importante trattato sulle coniche in 9 libri dei quali solo i primi 8 sono arrivati fino a noi.

Consideriamo dunque un cono retto. Per fissare anche visivamente i punti importanti della nostra costruzione, rappresentiamo in rosso la circonferenza base del cono e consideriamo rosso il piano di quella circonferenza. Ogni piano parallelo a quello intersecherà il cono lungo una circonferenza che rappresentiamo ancora in rosso. Su questi piani paralleli la forma si conserva e tutto ciò che accade su un piano si trasforma, per proiezione, anche sugli altri mantenendosi angoli e rapporti. Il piano della conica non parallelo ai piani rossi e non passante per il vertice, intersecherà il cono lungo una curva, la conica che vogliamo descrivere, che rappresentiamo in grigio e chiamiamo grigio quel piano.

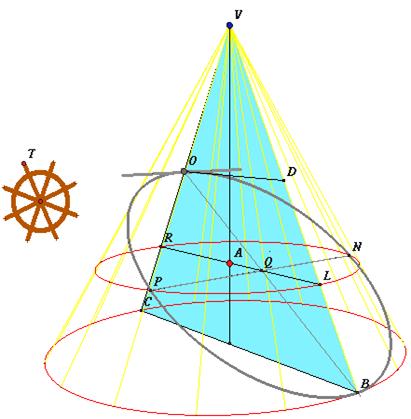
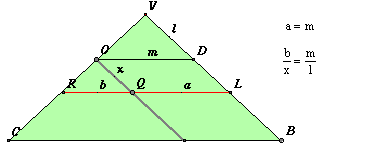
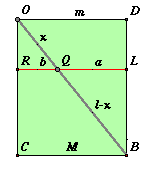
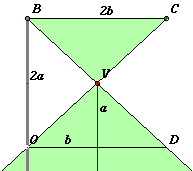
Il piano grigio interseca i piani di base rossi lungo rette parallele (disegnate in grigio)le quali intersecheranno o meno la circonferenza rossa di quel piano. La figura animata permette di traslare questi piani rossi agendo sul punto A. Fissiamo come piano di base iniziale quello per il quale la retta grigia è tangente alla circonferenza ("sopra" sarà esterna e "sotto" sarà secante), sia O il punto di tangenza e chiamiamo la retta tangente "retta delle ordinate". Sia OD il diametro della circonferenza rossa perpendicolare alla retta delle ordinate. Consideriamo ora un terzo piano verde, passante per l'asse e per OD. Poiché il cono è retto l'asse è perpendicolare alla base e quindi la retta delle ordinate sarà perpendicolare al piano verde essendo perpendicolare a due direzioni indipendenti (l'asse e il diametro OD) di quel piano.
Nella figura animata seguente abbiamo "smontato" i tre piani e li abbiamo messi uno accanto all'altro. Muovendo col mouse il punto A possiamo vedere la situazione sui tre piani man mano che A si avvicina al vertice.

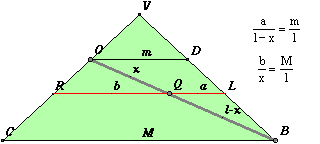
La conica sul piano grigio viene tracciata dal software come luogo riportando semplicemente, col compasso, su una retta orizzontale , al variare del punto A sull'asse, l' ascissa x = OQ ricavata dal triangolo verde e i corrispondenti segmenti verticali y = QP ordinati uno dopo l'altro e ricavati dalla circonferenza rossa variabile. Ci si rende facilmente conto di come sia a questo punto facile la trascrizione algebrica. Fissiamo una unità di misura per i segmenti e chiamiamo x la misura del segmento OQ, y la misura del segmento PQ, a e b le misure di LQ e QR rispettivamente. Osserviamo che sui cerchi rossi il segmento PQ è medio proporzionale tra LQ e QR cioè

LQ : PQ = PQ : QR

e quindi, passando alle misure

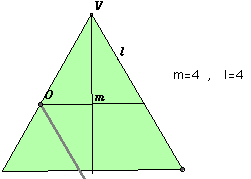
Il prodotto ab può essere calcolato a partire dalla posizione di Q (individuata dalla x) e dai dati del problema: l'apertura del cono e l'inclinazione del piano della conica, dati che variano a seconda del tipo di conica. Nel caso dell'ellisse la situazione sul piano verde si presenta come in figura dove abbiamo indicato con l,m,M,x i numeri che esprimono le misure dei segmenti che indicano. Usando le ovvie similitudini dei triangoli abbiamo:

e quindi, moltiplicando le due espressioni

(1)

dove la costante che moltiplica il fattore x(l-x) dipende solo dai dati del problema. L'espressione che abbiamo trovato è della massima importanza perché permette di calcolare data l'ascissa x , una ordinata y che descrive la nostra conica.

Nel caso della parabola abbiamo invece:

e quindi, moltiplicando le due espressioni

(2)

mentre per l'iperbole

e quindi, moltiplicando le due espressioni

(3)

I risultati che abbiamo ottenuto sono di estrema importanza: essi permettono di "disegnare per punti" i vari tipi di coniche specificando il valore della ordinata y da alzare in corrispondenza alla data ascissa x senza doversi riferire al cono che ha originato la curva. Ricapitolando abbiamo il seguente

Teorema di Apollonio
Consideriamo fissato nel piano un sistema di riferimento cartesiano. Dati due parametri p > 0 e q, il luogo dei punti di coordinate (x,y) che verificano l'equazione ¹

y² = px + qx²

(4)

è sempre una conica non degenere. La conica è una ellisse se q < 0, una parabola se q = 0 e una iperbole se q > 0.

La costruzione di Apollonio, percorsa a ritroso, permette anche, data l'equazione della conica, di trovare un cono che la contenga. Facciamo un esempio nel caso della parabola.

Esercizio
Data la parabola di equazione y²=4x trovare un cono retto e un piano di cui lei sia sezione.
Possiamo intanto disegnare la curva per punti servendoci anche di un calcolatore per renderci conto della sua forma

e poi per costruire il cono riferendosi alla figura relativa alla parabola, basterà trovare un triangolo isoscele la cui base m sia legata al lato obliquo l dalla relazione m²/l =4. Possiamo prendere, ad esempio, un triangolo equilatero, ruotarlo intorno alla sua altezza in modo da avere il cono e segare tale cono con un piano parallelo alla direttrice e passante per il punto O.

Se il punto O è distante dal vertice V del cono 4 unità (la stessa usata per disegnare la curva) allora la parabola che si ottiene è identica a quella che abbiano disegnato col calcolatore. Naturalmente questo è uno dei tanti coni circolari retti che contengono la nostra parabola.
Vari esercizi della stessa natura possono essere proposti per tutti i tipi di coniche.

Esercizio
Trovare, seguendo le stesse linee di Apollonio, l'equazione della curva ottenuta intersecando un cilindro retto con un piano.

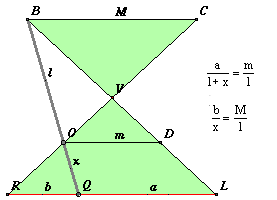
La situazione è identica al caso del cono, l'unica differenza è che ora m = M e quindi l'equazione della sezione diventa

(5)

Coni circolari e loro sezioni

3. Strumenti reali e strumenti virtuali per tracciare le coniche

Indichiamo ora un metodo del tutto elementare per risolvere in modo geometrico l'equazione della conica y² = px + qx², per trovare cioè la y data la x. Il metodo, di origine pitagorica, può essere utile per realizzare con dei software di geometria dinamica come Cabrì o Cinderella il disegno di una conica come luogo e visualizzare la sua forma a seconda dei valori dei parametri p e q. Il problema consiste nel trovare il lato y di un quadrato la cui area sia uguale a quella di un rettangolo di lati x e p+qx. Per ragioni di dimensioni il parametro p sarà rappresentato da un segmento, mentre il parametro q da un rapporto (una pendenza m:n) in modo qx possa essere rappresentato da un segmento, il quarto proporzionale nella proporzione m:n = x:qx. In questo modo l'equazione è traducibile in termini geometrici e la soluzione è facilmente costruibile. Nella figura animata che abbiamo realizzato, possiamo cambiare la grandezza del segmento p e modificare la pendenza q.

Fissato un segmento x iniziale su una retta orizzontale (l'asse delle ascisse) si costruisce il rettangolo rosso che è diviso in due parti: la prima di lati x e p e la seconda di lati x e qx. Questa seconda parte viene aggiunta nel caso dell'iperbole (nperbolh che significa eccesso, andare oltre) o tolta nel caso dell'ellisse (elleiyis che vuol dire mancanza, difetto, togliere) o ignorata nel caso della parabola (parabolh che vuol dire applicazione senza togliere o aggiungere nulla). Il segmento che rappresenta il lato del quadrato di area y² è costruito con la circonferenza rosa come quarto proporzionale tra x e p+qx. Questo segmento è poi riportato come ordinata sulla x. Il luogo è ovviamente descritto dal movimento di x lungo l'asse delle ascisse. Cambiando col mouse la pendenza q (q > 0, q = 0, q < 0) si passa da un tipo di conica a un'altra.

I termini con cui Apollonio chiama le coniche e che si usano nello stesso significato ancora oggi, sono diverse da quelli usati dai suoi predecessori (Archimede e Menecmo) e, secondo alcuni storici, essi derivano dagli antichi studi dei pitagorici sulla così detta applicazione delle aree. Si tratta, nel caso più semplice, dato un segmento a e un'area quadrata y², di "applicare" a quel segmento un altro segmento x in modo da formare un rettangolo di lati a e x e di area uguale a quella data (in termini numerici ax = y² applicazione parabolica), oppure si applica su a un segmento x in modo da formare un rettangolo di area uguale a quella data la cui base però è una parte di a e la parte mancante genera un quadrato (in termini numerici y²=ax-x² applicazione ellittica) o ancora si applica su a un segmento x in modo da formare un rettangolo di area uguale a quella data la cui base però eccede a di un quadrato (y²=ax+x² applicazione iperbolica). La soluzione geometrica di questi problemi che si basa sul teorema dello gnomone, forma il corpo principale delle tecniche di algebra geometrica nella matematica antica. Esse si riducono oggi alle formule risolutive per le equazioni di secondo grado.

I metodi scoperti da Apollonio permettono di disegnare facilmente, per punti e in modo esatto tutte le possibili coniche. Non sappiamo se tali metodi fossero noti nel rinascimento. Alberti e Piero della Francesca riconoscono chiaramente che lo scorcio di un cerchio è una sezione piana di un cono ma suggeriscono metodi empirici per disegnarlo. Leonardo inventa e probabilmente costruisce dei compassi in grado di tracciare esattamente le coniche. L'idea di Leonardo è molto semplice ma nello stesso tempo richiede un "ricentramento cognitivo". Normalmente pensiamo il compasso come uno strumento che con la sua rotazione genera un cono la cui sezione sul piano del foglio sempre orizzontale è una circonferenza. Il cono che immaginiamo ha la base circolare orizzontale e l'asse verticale. Se si vogliono ottenere da quel cono delle sezioni che non siano circolari diventa necessario intersecarlo con un piano obliquo cosa quanto mai complicata se si vuole disegnare il risultato di tale intersezione. L'idea di Leonardo è quella di inclinare l'asse intorno a cui ruota il compasso mantenendo invece orizzontale il foglio da disegno. In questo modo la gamba del compasso che contiene la mina, man mano che ruota appoggiandosi al foglio, mantenendo lo stesso angolo con l'asse fisso, cambia lunghezza. Basterà quindi inventare un meccanismo che permetta di adattare la lunghezza della gamba alle necessità. Una possibilità è ad esempio quella di far scorrere la gamba mobile in un binario facendola aderire al foglio sotto la pressione di un peso o della mano che la spinga in basso. Nel seguente compasso realizzato sulla base di progetti leonardeschi

l'asse è tenuto ben fermo dal treppiedi mentre la matita, che scorre in un suo binario, viene fatta scendere a mano. In quest'altro compasso realizzato pare per costruire specchi parabolici, il piano del foglio è opportunamente inclinato in modo da renderlo parallelo alla generatrice.

L'apertura del cono è di 45 gradi in modo da rendere più agevole fissare l'angolo (con una semplice squadretta) che non deve cambiare durante la rotazione attorno all'asse. Un peso, ben visibile spinge la matita verso il foglio.
Il contenuto matematico di questi strumenti è evidente: essi disegnano la curva che si ottiene intersecando un cono retto con un piano, dunque una conica.

Problema Le coniche si possono realizzare tutte su un cono retto e aperto a 90 gradi?

Coni circolari e loro sezioni

4. I luoghi del giardiniere: proprietà metriche di ellissi e iperboli

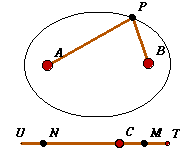
L'Ellisse viene spesso descritta (e definita) come luogo del giardiniere pensando che questa sia una via più semplice. L'origine di questa opinione si trova in un brano di Descartes nella sua Diottrica:

L'ellisse è una linea curva che i matematici son soliti rappresentare tagliando obliquamente un cono o un cilindro e che talvolta ho visto servire ai giardinieri nella divisione delle aiuole ove questi la descrivono certamente in modo assai grossolano e impreciso, ma che tuttavia mi pare faccia comprendere la sua natura meglio della sezione di un cilindro o di un cono.

Il modo del giardiniere è quello di tendere una corda abbastanza lunga tra due pali fissi. La figura animata descrive questa costruzione

Fissati i due punti A e B e un segmento UT si cerca il luogo dei punti P del piano per i quali la somma

AP + BP = costante

o, se si vuole, per i quali la distanza da A sommata a quella da B è uguale alla lunghezza costante del segmento UT.
Per dimostrare che questa curva è una ellisse, cioè la sezione di un cono con un piano che incontra tutte le generatrici, cerchiamo l'equazione cartesiana del luogo e vediamo se possiamo ridurla a quella dell'ellisse. Per questo scopo fissiamo un sistema di riferimento cartesiano che abbia l'origine nel punto medio tra A e B e come asse delle x la retta AB. Le coordinate dei punti A e B saranno: A=(-c,0) e B=(c,0).

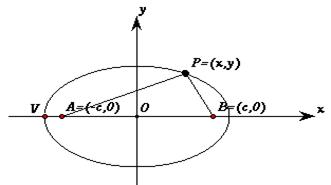
Usando il teorema di Pitagora (la formula della distanza tra due punti) per calcolare la distanza tra PA e PB, dopo semplici passaggi algebrici troviamo l'equazione

(6)

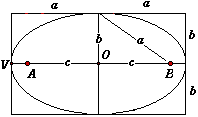
dove (a,0), (-a,0) e (0,b), (0,-b) rappresentano i punti di intersezione della curva con gli assi coordinati. Per dimostrare che questa curva dalla forma ovale è di fatto una ellisse, cioè la sezione con un cono, vediamo come diventa la sua equazione se prendiamo come asse delle ordinate la retta verticale per V=(-a,0)di modo che la curva sia riferita agli assi nello stesso modo in cui lo è quella di Apollonio.

Se un punto P ha le coordinate (x,y) nel vecchio sistema di riferimento, in quello nuovo avrà la stessa ordinata Y=y e l'ascissa X=x+a essendo a la distanza di V da O. Lo stesso punto P insomma sarà rappresentato dalla coppia (x,y) nel vecchio sistema di coordinate e dalla coppia (x+a,y) in quello nuovo. Le formule che permettono di passare da un sistema di coordinate a un'altro sono dunque

e dunque nelle nuove coordinate (X,Y) il punto dovrà verificare l'equazione

che, a conti fatti, risolvendo l'equazione rispetto a Y² diventa

che, in virtù del teorema di Apollonio rappresenta una ellisse essendo il fattore q = -b²/a² negativo.
Notiamo che, scrivendo l'equazione nella forma

(7)

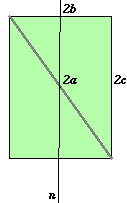
possiamo facilmente confrontarla con la (5) e riconoscereY la forma di un cilindro di cui l'ellisse è sezione

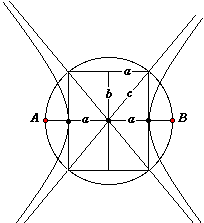
basterà ruotare attorno all'asse n il rettangolo di lati 2b diagonale 2a. Il cilindro ottenuto conterrà l'ellisse come intersezione col piano passante per la diagonale e disegnata in grigio e perpendicolare al piano del rettangolo.
L'analisi che abbiamo effettuato ha messo in luce nuove caratteristiche metriche proprie dell'ellisse in particolare ha fatto emergere l'esistenza di due punti A e B detti fuochi e un centro di simmetria O: un punto (x,y) dell'ellisse infatti ne individua un'altro (-x,-y) simmetrico rispetto ad O che sta ancora sull'ellisse. Oltre al centro di simmetria abbiamo anche due assi di simmetria uno maggiore, di lunghezza 2a, detto asse maggiore e l'altro minore di lunghezza 2b detto asse minore. Questo perché un punto (x,y) dell'ellisse ne individua sempre un'altro (x,-y) simmetrico rispetto all'asse maggiore e (-x,y) simmetrico rispetto all'asse minore. Queste simmetrie (unite alla simmetria identica) formano un gruppo detto il gruppo di Klein e ogni curva la cui equazione contiene solo combinazioni di termini in x² e y² ha, per lo meno, questo gruppo di simmetrie semplicemente perché (+1)²=1².
L'equazione (7) che abbiamo trovato, che potremmo chiamare l'equazione di Apollonio dell'Ellisse, mette chiaramente in evidenza oltre alla sua parentela, come abbiamo visto, con un cilindro che la contiene, anche l'espressione dei suoi assi 2b e 2a il cui rapporto (sempre minore di 1) al quadrato fornisce il coefficiente del termine di secondo grado in x. Dati i semiassi a e b non è difficile trovare la posizione dei fuochi e la lunghezza costante della "corda" con cui "il giardiniere" traccia l'ellisse: abbiamo infatti che la lunghezza della "corda" è data da AV+VB=(a-c)+(a+c)=2a e quindi la distanza c dei fuochi dal centro risulta essere data da

L'interesse di queste formule è che tutto è espresso in termini del rettangolo di lati 2a e 2b entro il quale l'ellisse si inscrive.

La forma dell'ellisse fa pensare a una circonferenza "schiacciata" lungo una direzione. Questa intuizione può essere precisata in modo rigoroso e quindi verificata. Possiamo pensare allo "schiacciamento" lungo una data direzione, ad esempio quella verticale, come a una trasformazione che accorcia tutte le lunghezze verticali secondo un fissato rapporto (minore di uno se si parla di schiacciamento o contrazione). La figura animata seguente contrae l'ordinata della circonferenza relativa al punto P di un fissato valore dato dal rapporto AT:AB=b:a.

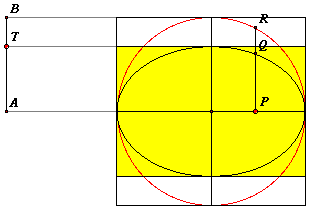
Per ogni posizione del punto P abbiamo sempre PQ:PR=AT:AB. Muovendo il punto P si può constatare come riducendo le ordinate del cerchio PR del dato rapporto si ottenga lo schiacciamento della circonferenza. Se invece modifichiamo il rapporto b:a agendo sul punto T abbiamo l'impressione di vedere un disco che ruota attorno al proprio diametro orizzontale.
Che questa curva sia di fatto una ellisse si vede facilmente in modo analitico. Fissiamo un sistema di riferimento cartesiano con l'origine nel centro della circonferenza e gli assi paralleli alle direzioni del quadrato. Sia AB=a e AT=b (b < a) e k=b/a il rapporto di contrazione. Se il punto R ha le coordinate (x,y) il punto Q ottenuto contraendo col coefficiente k la sua ordinata avrà le coordinate Q=(x,ky) e quindi se il punto R sta sulla circonferenza, cioè se la sua distanza da O è uguale ad a, allora

x²+y²=a²

e quindi il punto P=(x,ky) verificherà l'equazione

che si riconosce subito essere l'equazione di una ellisse di semiassi a e b.
Un altro modo, forse più semplice, per descrivere la contrazione della circonferenza è disegnare un'altra circonferenza interna concentrica di raggio b.

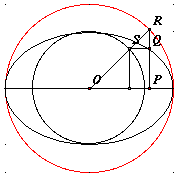
Un raggio OR interseca la circonferenza interna nel punto S. Per trovare il punto Q facciamo la parallela SQ fino ad incontrare la verticale PR, il rapporto PQ:PR , per ovvi motivi di similitudine, non dipende dalla scelta di OR dal momento che coincide col rapporto fissato tra i raggi b=OS ed a=OR.
Questo punto di vista dal quale guardare l'ellisse può essere utile per calcolarne l'area seguendo l'idea e la strada indicata da Keplero. Se sottoponiamo il piano a una contrazione di un fattore k lungo una data direzione, diciamo verticale, ogni quadrato di lati verticali e orizzontali si contrarrà in un rettangolo la cui base orizzontale non cambia mentre l'altezza si contrae di un fattore k. Il rapporto tra l'area del rettangolo e quella del quadrato sarà quindi k. Poiché possiamo approssimare una qualunque area con una somma di quadratini sempre più piccoli, l'area della figura contratta sarà approssimata dai corrispondenti rettangolini sempre più piccoli e il rapporto complessivo tra questi due valori approssimati sarà sempre k. Dal momento che possiamo migliorare la nostra approssimazione quanto vogliamo, al limite sarà ancora k il rapporto tra le aree. Nel caso dell'ellisse e della circonferenza abbiamo

e quindi l'area dell'ellisse di semiassi a e b è data dalla semplicissima formula

Area Ellisse = pab.

Anche l'iperbole ha proprietà focali analoghe a quelle dell'ellisse.

Data una iperbole, cioè una sezione di un cono con un piano non passante per il vertice e parallelo a due generatrici, esistono sempre, su quel piano, due punti A e B detti fuochi tali che la differenza delle distanze

AP - BP = costante

non dipende cioè dal punto P sull'iperbole. Viceversa, dati A e B, il luogo dei punti del piano per i quali la differenza delle distanze da A e B è costante, è un'iperbole. Tutta la teoria analitica procede esattamente come nel caso dell'ellisse, stessi calcoli, stesse semplificazioni, stessi ragionamenti, l'unica differenza consiste nel segno: un + che diventa un -. Ben poca cosa se si pensa a come spesso i segni siano trattati con distrazione come se contassero poco o nulla e invece, in questo caso, il cambiamento di segno produce dal punto di vista della forma, una grandissima differenza. L'ellisse è tutta chiusa nella sua scatola, mentre l'iperbole è formata da due rami che corrono all'infinito lungo due direzioni diverse, da lati opposti. Desargues riuscirà a immaginare quelle due metà opposte schiena a schiena saldarsi all'infinito. Dirà Sinisgalli ² dell'iperbole che

...è una curva sbracata, un desiderio che vuole afferrare con due braccia l'assoluto.

...una traccia che si perde e che ritorna, che scompare e ricompare, una curva che ci apre la porta dell'Aldilà, poi la richiude, e dopo essersi così infinitamente perduta, ritorna dalla porta di dietro...

Il termine stesso iperbolico, nel linguaggio comune diventa la metafora di qualcosa di illimitato di fuori dalle righe.

La formula (6) che esprime l'equazione cartesiana dell'ellisse nel riferimento che ha l'origine nel centro, diventa, nel caso dell'iperbole

(8)

dove 2a rappresenta la costante AP-PB, a < c, e il coefficiente b è legato ad a e c dalla relazione

La presenza di soli termini quadrati nell'equazione (8) ci dice che il gruppo di Klein è il gruppo di simmetria della curva. E dunque c'è un centro do simmetria, il punto O e due assi di simmetria. I due punti (-a,0) e (a,0) rappresentano l'intersezione della curva con l'asse delle ascisse.
Traslando l'asse delle ordinate questa volta verso destra si ottiene l'equazione di Apollonio dell'iperbole nella forma

(9)

Da questa equazione riesce agevole trovare un cono e un piano la cui intersezione sia l'iperbole assegnata. Riferendoci all'espressione (3) che fornisce l'equazione di una iperbole a partire da un cono, possiamo, viceversa, costruire il cono a partire dall'iperbole.

Prendiamo un triangolo rettangolo di cateti a e b e ruotiamo attorno l'ipotenusa attorno al cateto di lunghezza a. Otteniamo un cono retto. Se intersechiamo questo cono col piano passante per i punti O e B e perpendicolare al piano del triangolo, otteniamo una iperbole che ha come equazione la (9) e che dunque è l'iperbole da cui siamo partiti. Notiamo che il piano passante per il vertice del cono parallelo al piano dell'iperbole contiene le due generatrici che l'iperbole non incontra, l'angolo tra queste generatrici che è l'angolo di apertura del cono corrisponde all'angolo tra gli asintoti dell'iperbole che sono quelle rette, passanti per il centro cui l'iperbole tende senza mai raggiungere. Guardando la figura si vede che l'apertura del cono è data dal rapporto b/a: questo permette di dare un significato geometrico al parametro b che interviene nell'equazione dell'iperbole esso infatti definisce la pendenza degli asintoti.
La figura seguente mostra il legame tra i parametri a e b che intervengono nell'equazione e il loro significato geometrico

Abbiamo indicato in nero i vertici dell'iperbole, in rosso i fuochi A e B, c è legato ad a e b dalla relazione c²= a²+b², mentre la pendenza m che corrisponde all'angolo di apertura del cono è data da

Coni circolari e loro sezioni

5. Eque e non eque distanze tra punti e rette:eccentricità e direttrici

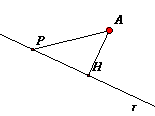
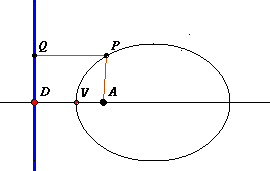
Data una retta r e un punto A la distanza di A da r viene definita come la lunghezza del segmento AH perpendicolare a r.

se P è un qualunque punto della retta diverso dal piede H della perpendicolare allora AP>AH essendo in ogni triangolo rettangolo l'ipotenusa più lunga di un cateto e quindi la distanza di A da r è la minima lunghezza dei segmenti che uniscono A con un punto di r.
Dati A ed r vogliamo trovare tutti i punti del piano (individuato da A ed r) che sono equidistanti dal punto e dalla retta. Più in generale, dato un determinato rapporto p:q cerchiamo il luogo dei punti P del piano per i quali il rapporto tra la distanza AP e Pr è come p:q. Il problema è molto complicato dal punto di vista sintetico per questo cerchiamo una soluzione per via analitica cercando di descrivere il luogo incognito con una equazione che, in un secondo tempo, cerchiamo di reinterpretare geometricamente.
Notiamo intanto che possiamo facilmente trovare almeno un punto del nostro luogo: dividiamo il segmento AH con un punto V in modo che le due parti trovate siano nel rapporto p:q. Il punto V sarà allora un punto del luogo. Scegliamo le coordinate prendendo come origine il punto V che abbiamo trovato e come asse delle ascisse la retta AH.

A avrà le coordinate A=(p,0) e la retta r l'equazione x = -q. Se P=(x,y) è un qualunque punto del piano il rapporto tra la sua distanza da A e quella da r è come p:q se e solo se

dove abbiamo indicato con e il valore del fissato rapporto p:q. Svolgendo i calcoli con semplici passaggi troviamo l'equazione

(10)

Usando ora il teorema di Apollonio, possiamo interpretare geometricamente questa equazione concludendo che il luogo incognito è una conica ed esattamente è una ellisse se 0 < e < 1 e una iperbole se e > 1, come risulta immediatamente confrontando l'equazione (10) con la (4). Nel caso sia e = 1 conviene riscrivere la (10) nella forma

che per e = 1 diventa

y²=4px

(11)

equazione che rappresenta una parabola della quale si riconosce facilmente il cono di cui è sezione ragionando come nell'esempio y²=4x dove avevamo preso un cono aperto a 60 gradi.


Questo nuovo punto di vista arricchisce molto la geometria dell'ellisse e dell'iperbole. Confrontando la (10) con le equazione (7) e (9) vediamo che i parametri a e b, che individuano univocamente la conica, sono espressi in termini di questi nuovi invarianti

Nel caso dell'iperbole cioè nel caso che sia e > 1, sciogliendo i valori assoluti, troviamo

e poiché c-a è la distanza del fuoco dal vertice dell'iperbole, il punto A è il fuoco dell'iperbole.
Nel caso dell'ellisse abbiamo 0 < e < 1 e quindi

e otteniamo ancora che A è il fuoco dell'ellisse. Ricapitolando, nel caso di distanze non eque, abbiamo ottenuto il sorprendente risultato

Teorema
Dato un punto A e una retta r che non contiene A, il luogo dei punti P del piano per i quali la distanza di P da A è più piccola della distanza di P da r secondo uno stesso rapporto e è una ellisse che ha il fuoco nel punto A. Il luogo dei punti, invece, per i quali la distanza di P da A è più grande della distanza di P da r secondo uno stesso rapporto e è una iperbole che ha il fuoco nel punto A.

La figura animata seguente permette di cambiare il valore di e detto eccentricità e vedere il luogo che ne deriva.

L'analisi che abbiamo compiuto mette in luce nuove caratteristiche metriche delle ellissi e delle iperbole: accanto ad ogni fuoco esiste una retta, detta direttrice, perpendicolare all'asse maggiore posta a una distanza dal centro della conica data da a²/c. Infatti, nel caso dell'ellisse, a è la distanza del vertice dal centro della conica e q è la distanza della direttrice dal vertice quindi q+a è la distanza della direttrice dal centro. Abbiamo dunque

e analogamente per l'iperbole. La direttrice ha la notevole la proprietà mantenere costante il rapporto tra la lunghezza di un raggio focale AP con la distanza di P da tale retta: tanto il raggio focale si allunga tanto la distanza di P dalla direttrice aumenta, tanto il raggio focale si accorcia tanto si accorcia quella distanza. Cosa accade nel caso che la lunghezza del raggio focale non cambi? Guardando la nostra figura animata ci accorgiamo che allontanando la direttrice dal punto A la conica tende a una circonferenza. Poiché in quel caso il rapporto e tende a 0, possiamo dire che la circonferenza è una conica di eccentricità nulla con la direttrice all'infinito. La cosa è coerente con l'equazione (10) che per e = 0 diventa y²=x(2p-x) che rappresenta appunto una circonferenza di raggio p e centro nel punto A=(p,0).

Coni circolari e loro sezioni

6. Proprietà focali della parabola

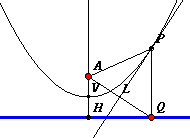
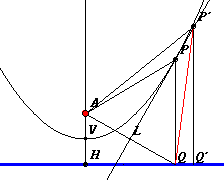
Anche il caso della parabola è estremamente interessante perché ci permette di considerare questa curva da un'altro punto di vista che ne evidenzia una nuova geometria. Ogni la parabola infatti, la cui equazione può essere sempre scritta nella forma y²=kx, ha al suo interno un punto A, privilegiato, che si trova sull'asse di simmetria (l'asse delle ascisse) a una distanza dal vertice pari alla quarta parte di k (punto che ancora diremo fuoco della parabola) e al suo esterno una retta r perpendicolare all'asse di simmetria e alla stessa distanza di A dal vertice, e i punti della parabola risultano tutti equidistanti da A e da r. La parabola insomma è la linea di equilibrio delle distanze tra un punto e una retta. Anche in questo caso la retta r è chiamata direttrice della parabola. Questa caratteristica permette di impostare una semplice costruzione geometrica realizzabile coi software di geometria dinamica che disegna la parabola come luogo di equidistanza. La seguente figura animata costruisce una parabola in questa maniera

Questa costruzione suggerisce una nuova proprietà della parabola di grandissima utilità nella tecnologia.

Teorema sul fuoco della parabola
Sia A il fuoco, r la direttrice di una parabola e P un suo punto. La tangente alla parabola in P è la bisettrice dell'angolo APQ (Q è il piede della perpendicolare da P a r).

Se la bisettrice non fosse tangente³ intersecherebbe la parabola in un'altro punto P'.

Essendo P' sulla parabola dovrebbe essere AP' = P'Q', ma essendo anche sulla bisettrice PL che è l'asse del segmento AQ, dovrebbe essere AP' = P'Q dal che si dedurrebbe che in un triangolo rettangolo l'ipotenusa P'Q è uguale al cateto P'Q' cosa manifestamente assurda.

Supponendo che i raggi di luce si riflettano su una superficie liscia formando angoli uguali, come viene implicitamente supposto dallo stesso Euclide nel teorema 19 dell'Ottica, un raggio di luce parallelo all'asse della parabola, essendo il prolungamento di PQ, si rifletterebbe nel fuoco, e quindi sarebbe possibile concentrare in un unico punto l'energia di infiniti raggi che raggiungessero paralleli tra loro uno specchio parabolico.

Esercizio sull'assedio di Siracusa
Calcolare la grandezza di un eventuale specchio parabolico con il fuoco lontano 50 metri (tanto possiamo supporre fosse almeno la distanza delle navi romane dai torrioni di Siracusa) dal vertice

Se, per una parabola, scegliamo un sistema di riferimento cartesiano cha abbia l'asse delle ordinate parallelo all'asse della parabola, questa curva diventa tra tutte le coniche l'indiscussa protagonista. In questo caso infatti, se l'asse delle ordinate coincide con l'asse della parabola, la sua equazione si ottiene dalla (11) cambiando x con y:

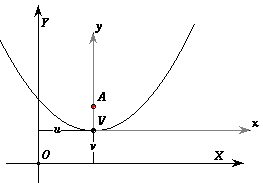
mentre, in generale, se V =(u,v) sono le coordinate del vertice nel nuovo sistema di coordinate,

abbiamo:

e quindi l'equazione della parabola nel nuovo sistema di riferimento diventa:

che è della forma

dove il coefficiente a (non nullo) è responsabile dell'apertura della parabola e quindi della posizione del fuoco, il coefficiente b dell'ascissa del vertice e il coefficiente c dell'ordinata. Il caso in cui il coefficiente a=1/4p fosse negativo si riduce al precedente cambiando i segni delle ordinate il che significa ribaltare la curva rispetto all'asse delle ascisse. Possiamo allora concludere col seguente enunciato:

Teorema (parabole ed equazioni)
In un sistema di riferimento cartesiano l'equazione y = ax² + bx + c rappresenta , se a non è zero, una parabola con la concavità rivolta nella direzione dell'asse y se a > 0 nella direzione opposta se a < 0. Inoltre, più il parametro a è grande più la distanza p del fuoco dal vertice diventa piccola secondo la formula 4ap=1.

La teoria delle equazioni di secondo grado ha in questo modo una sua efficacissima rappresentazione geometrica, le radici dell'equazione corrispondono ai punti in cui y=0 cioè ai punti in cui la parabola interseca l'asse delle ascisse, l'esistenza o meno di queste radici dipende dalla posizione del vertice della parabola rispetto agli assi e dalla sua concavità, la simmetria del piano rispetto all'asse della parabola è quella trasformazione che muta l'equazione in se poiché scambia tra loro le due radici. Il gruppo di simmetria della parabola, formato dall'identità e dalla simmetria rispetto all'asse è quello che si chiama, nell'algebra contemporanea, il gruppo di Galois dell'equazione ax² + bx + c =0. L'immagine geometrica che la parabola suggerisce rispetto alla teoria delle equazioni di secondo grado è tutt'altro che ingenua, essa aiuta il pensiero a meglio capire il senso dell'algebra che ne è soggiacente e apre la mente verso possibili nuove visioni di cui quella è solo un esempio.
Possiamo, su queste basi, sviluppare vari esercizi dove si chiede di ricavare a partire dall'equazione della parabola le sue caratteristiche geometriche: posizione dell'asse di simmetria, del vertice e del fuoco. E viceversa a partire dalla forma della parabola e dalla sua posizione rispetto agli assi si chiede di ricavare informazioni algebriche sull'equazione: esistenza o meno di radici reali, numero di radici, semi somma delle radici in relazione all'asse della parabola ecc.