Compenetrazione di solidi
Compenetrazione di solidi
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Compenetrazione di solidi
Un problema grafico che si presenta molte volte nella rappresentazione di componenti meccanici consiste nella determinazione delle linee di intersezione di parti solide o cavità.
Il problema non ha solo interesse geometrico, ma trova applicazione pratica in diversi rami dell’ingegneria: basti pensare alle ramificazioni di condotte, nel campo impiantistico, oppure al caso di pezzi attraversati da scanalature o da fori che possono essere appunto considerati come solidi cavi.
Ai fini della determinazione delle line di intersezione, è opportuno distinguere i casi di compenetrazione tra:
- compenetrazioni tra solidi prismatici (in questo caso tutte le intersezioni tra facce piane sono linee rette):
- compenetrazioni tra solidi prismatici e solidi di rivoluzione;
- compenetrazioni tra solidi di rivoluzione (che ricorre di frequente in connessioni di tubature o innesti di condotte in contenitori cilindrici o prismatici).
Per il tracciamento delle linee di intersezione di solidi compenetrati esistono diverse metodologie.
Solitamente, comunque, le curve di intersezione si tracciano per punti: si determina cioè un numero sufficiente di punti appartenenti contemporaneamente a entrambe le superfici dei solidi compenetrati; i punti vengono poi uniti con segmenti o curve a seconda dei casi.
La curva risultante dall’intersezione di due solidi, chiamata figura di intersezione, osemplicemente intersezione, risulterà quindi spesso approssimata.
Compenetrazione tra solidi prismatici
L’intersezione fra due piani è un segmento di retta: quindi, se due solidi sono compenetrati da solidi delimitati da facce piane, la figura di intersezione sarà composta da segmenti di retta.
La figura 15 mostra le proiezioni ortogonali di un prisma retto a base quadrata con un foro quadrato, considerabile quindi come l’intersezione del prisma con un altro prisma ancora a base quadrata. La costruzione geometrica delle linee di intersezione può avvenire a partire dal prospetto e dalla pianta; i punti B3 = A3 e B3’= A3’ della vista laterale si ottengono come proiezioni di punti gia definiti nel primo e secondo piano di proiezione.
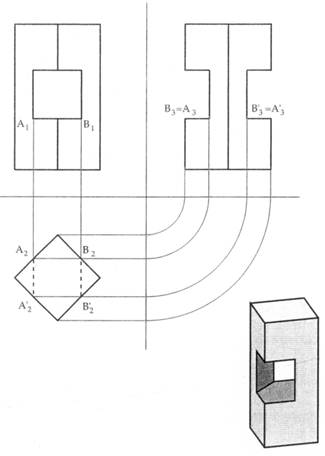
Figura 15 – “Intersezione” di un prisma retto con un foro prismatico
Nelle figure 16 e 17 si hanno costruzioni analoghe con diverse posizioni dei prismi.
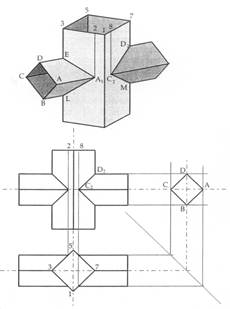
Figura 16 – Intersezione di due prismi Figura 17 – Intersezione di prismi retti ad assi
retti ortogonali sghembi
Compenetrazione tra solidi prismatici e di rivoluzione
Nella figura 18 è illustrato il disegno della compenetrazione tra un cilindro ad asse verticale e un prisma retto a sezione quadrata, ad asse orizzontale. In questo caso la linea di intersezione in pianta è definita da due archi di circonferenza. Le intersezioni tra le facce a e a’ del prisma col cilindro sono i segmenti A2B2 e C2D2, che si ottengono mandando le linee di richiamo da A1≡B1 e C1 ≡D1 sino ad intersecare le tracce dei piani b e b’. Sul p.l. ritroviamo i segmenti A3B3 e C3D3.
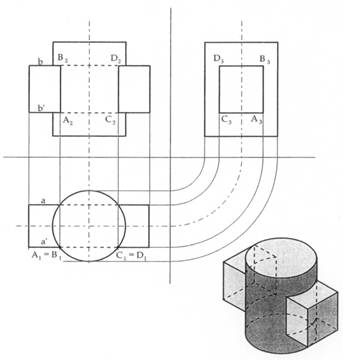
Figura 18 – Intersezione fra un cilindro e un prisma retti ad assi ortogonali
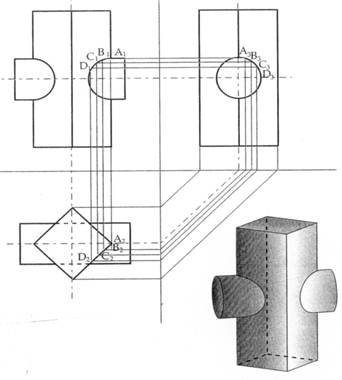
Se
il cilindro è ad asse orizzontale ed interseca il prisma ad asse verticale come in figura 19, le intersezioni sono dei tratti di curva. La figura illustra il procedimento per tracciare le intersezioni sul prospetto avendo già tracciato il profilo e la pianta. In questo caso si possono prendere dei punti qualsiasi sul cilindro nel p.l., come A3, B3, C3 e D3, e disegnare le linee di richiamo nel p.o., determinando i punti corrispondenti A2, B2, C2 e D2; le intersezioni corrispondenti delle linee di richiamo sul p.v. consentiranno la costruzione per punti delle due curve di compenetrazione sul prospetto.
Figura 19 – Intersezione fra un prisma verticale e un cilindro orizzontale
Le figure 20 e 21 chiariscono altri procedimenti per ottenere le linee di compenetrazione tra solidi prismatici e di rivoluzione.
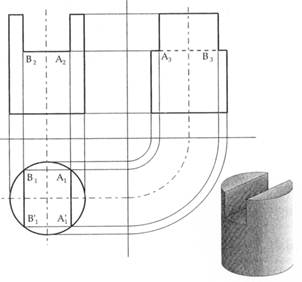
Figura 20 – Il taglio trasversale può essere considerato come un prisma che interseca il cilindro
Figura 21 – Il pezzo rappresentato può essere considerato come sovrapposizione di un cilindro e di un prisma a facce arrotondate oppure, come in questo caso, come intersezione fra cilindro e prisma
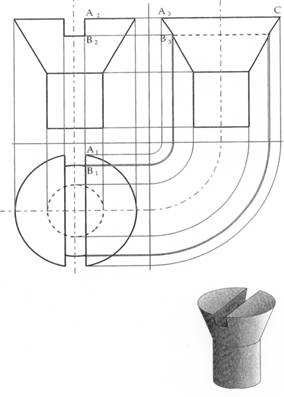
Figura 22 – La scanalatura della testa di una vite rappresenta un esempio tipico di intersezione tra un tronco di cono e un elemento prismatico. Dopo aver costruito il prospetto e la pianta, le intersezioni corrispondenti nel p.l. consentiranno la costruzione della linea A3B3
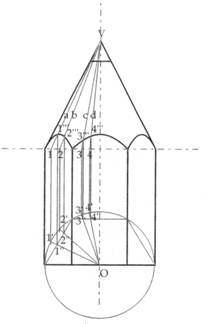 Un altro semplice esempio di questo tipo di compenetrazione è rappresentato dalla punta della matita prismatica sulla quale risulta ben visibile una curva di compenetrazione ottenuta dall’intersezione di un cono e un prisma esagonale (fig. 23).
Un altro semplice esempio di questo tipo di compenetrazione è rappresentato dalla punta della matita prismatica sulla quale risulta ben visibile una curva di compenetrazione ottenuta dall’intersezione di un cono e un prisma esagonale (fig. 23).
Figura 23 – Nell’estremità di una matita si ha l’intersezione di un prisma esagonale con un cono.
Per determinare le curve di intersezione, dal vertice V del cono si conducono alcune generatrici, quali a, b, c, d, fino ad incontrare la linea di intersezione dei due solidi nei punti 1, 2, 3, 4. Da questi punti si conducono delle linee verticali fino ad incontrare la proiezione circolare della base del cono nei punti 1’, 2’, 3’, 4’. Congiungendo questi punti col centro della circonferenza, si intercettano sull’esagono inscritto nella circonferenza i punti 1”, 2”, 3”, 4”, da cui si fanno partire delle linee verticali, le cui intersezioni con le generatrici di partenza danno i punti 1’’’, 2’’’, 3’’’, 4’’’ cercati
Una intersezione simile, fra un prisma retto ed un cono di grande apertura, si ha nei dadi esagonali (fig. 24).
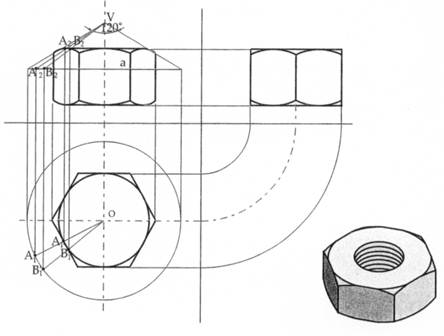
Figura 24 – Anche in un dado si trova l’intersezione fra prisma esagonale e cono. La costruzione delle curve di intersezione è analoga al caso precedente. A partire dal vertice del cono si conducono alcune generatrici a piacere fino ad incontrare la linea orizzontale a, considerata come proiezione della base del cono. Dai punti di intersezione, si conducono delle linee verticali, fino ad incontrare la proiezione circolare della base del cono nei punti A1’ e B1’. I punti della curva di intersezione si determinano come nel caso precedente
Compenetrazione tra solidi di rivoluzione
La figura 25 mostra casi di intersezioni frequenti tra cilindri.
Nei cilindri che si intersecano ortogonalmente, quando i raggi dei due solidi sono molto differenti, si preferisce l’approssimazione con un segmento (a); se la differenza è meno elevata, la curva di intersezione è approssimata da un arco di raggio r uguale al raggio del cilindro maggiore (b); nel caso di cilindri di eguale diametro, le linee di intersezione degenerano in segmenti di retta (d, f).
In tutti gli altri casi, si preferisce far uso di semplici costruzioni per l'ottenimento della curva. A questo proposito è possibile usare tre metodi differenti: il metodo delle generatrici, il metodo dei piani ausiliari e il metodo delle sfere ausiliarie.
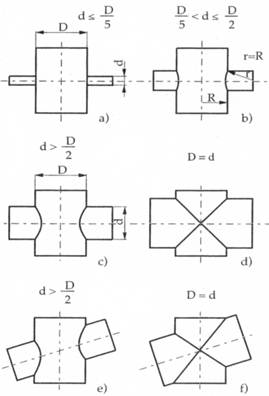
Figura 25 – Intersezioni fra cilindri: alcune rappresentazioni vengono semplificate
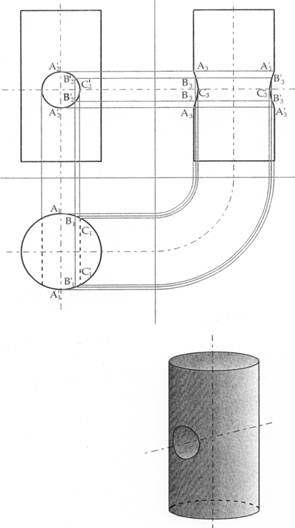
Metodo delle generatrici
Le linee di intersezione si tracciano per punti, individuando le generatrici del cilindro di diametro minore e determinando i punti di intersezione tra i due cilindri nelle diverse viste.
Tipico è il caso di un cilindro attraversato da un foro (fig. 26). I punti delle linee di intersezione nella terza vista sul p.l. vengono determinati scegliendo a piacere alcuni punti sulle generatrici A, B e C del cilindro di diametro minore (foro) sul p.o. e sul p.v.. Proiettando i punti sul p.l., si ottengono le linee di intersezioni dei due solidi.
Figura 26 – Ricerca della intersezione tra due cilindri col metodo delle generatrici
Metodo dei piani ausiliari
Si utilizzano dei piani ausiliari che taglino le superfici dei due solidi secondo curve piane, i cui punti comuni appartengono alla figura di intersezione cercata.
E’ opportuno scegliere i piani ausiliari in modo da ottenere linee e curve semplici.
Il procedimento per ritrovare la curva di intersezione tra due cilindri con questo metodo è illustrato nelle figure 27 (in cui il metodo di rappresentazione adottato è quello americano, con vista superiore, ovvero dall’alto, incompleta) e 28, con riferimento a due cilindri perpendicolari nel primo caso e a due cilindri con assi inclinati nel secondo.
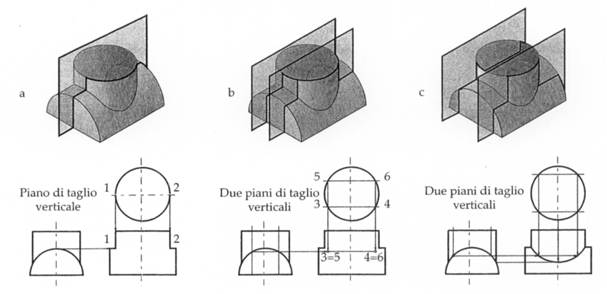
Figura 27 - Intersezione di cilindri ad assi ortogonali col metodo dei piani ausiliari. Si possono usare progressivamente una serie di piani ausiliari che determinano nella vista principale il luogo dei punti della curva di intersezione:
a) il piano verticale contenente gli assi dei due cilindri stabilisce la posizione dei primi due punti di intersezione 1 e 2;
b) altri due piani paralleli a quello precedente determinano quattro ulteriori punti di intersezione 3, 4, 5 e 6;
c) altri piani determinano altri punti che saranno connessi con una curva
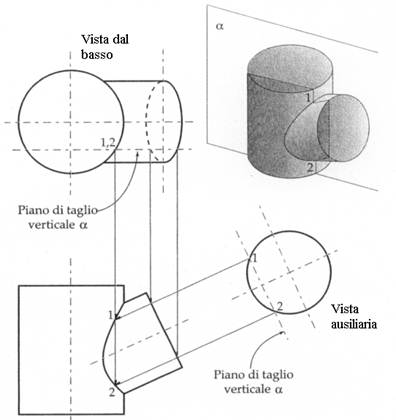
Figura 28 – Intersezione di cilindri ad assi inclinati con il metodo dei piani ausiliari. Per trovare l’intersezione dei cilindri, è possibile usare una vista ausiliaria; disegnando la traccia del piano di taglio α sulla vista ausiliaria e su quella superiore (vista dal basso), i punti di intersezione determinano la forma della curva sulla vista anteriore (prospetto)
Metodo delle sfere ausiliarie
Col metodo delle generatrici sono necessarie tre viste per poter ricavare le linee di intersezione; col metodo delle sfere ausiliarie è sufficiente una sola vista, ma può essere usato solo nei casi di compenetrazione di solidi di rotazione ad assi concorrenti.
Per risolvere il problema di ricavare la linea di intersezione, si considerano più sfere ausiliarie, con centro nel punto in cui si intersecano gli assi dei due solidi (fig. 29).
Il problema si risolve determinando i punti di intersezione delle circonferenze determinate dalle intersezione delle sfere con i cilindri e costruendo per punti le linee di intersezione.
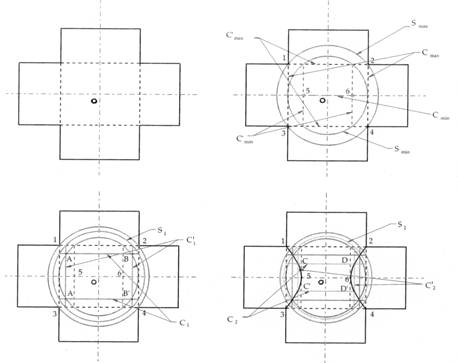
Figura 29 – Metodo delle sfere ausiliarie. Una volta disegnate le due sfere limiti Smax e Smin di centro O, si determinano le tracce delle due circonferenze sui cilindri verticale e orizzontale (Cmax e Cmin). Le intersezioni tra queste circonferenze darà luogo ai punti 1, 2, 3, 4, 5 e 6 per i quali dovranno passare le intersezioni cercate. Ripetendo la costruzione per le sfere S1 e S2 di raggio intermedio, si possono costruire per punti le linee di intersezione
La figura 30 illustra il caso dell’intersezione di un cono retto con un cilindro orizzontale.
 anche sul p.v.
anche sul p.v.
Infine, le due figure seguenti 31 e 32 illustrano due casi frequenti di compenetrazioni nei componenti meccanici.
A questo riguardo è opportuno ricordare che, ai fini delle intersezioni, i fori sono trattati come corpi cilindrici.
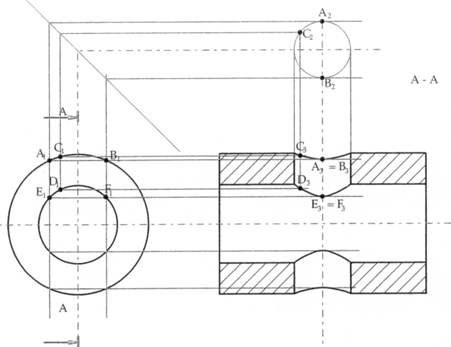
Figura 31 – L’intersezione tra due fori perpendicolari in un corpo cilindrico viene trattata come intersezione di cilindri cavi; la costruzione viene semplificata con la costruzione della vista ausiliaria, sulla quale è possibile individuare alcuni punti che permetteranno la costruzione delle curve di intersezione con la regole già viste
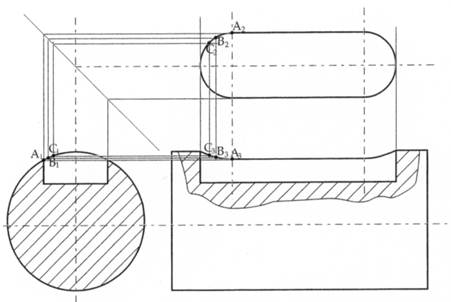
Figura 32 - La cava per linguetta è un caso pratico di intersezione tra elementi cilindrici e prismatici; anche in questo caso si può ricorrere ad una vista ausiliaria della cava, sulla quale si possono prendere alcuni punti a piacere e ricondursi così ai casi precedenti
Fonte: ftp://ftp.aula.dimet.unige.it/squarzoni/DTN1%202008.09%20-%20Cap.%2005%20Sezioni,%20intersezioni%20e%20sviluppi%20di%20solidi%20elementari.doc
Sito web da visitare: http://unige.it/
Autore del testo: non indicato nel documento di origine
Nota : se siete l'autore del testo sopra indicato inviateci un e-mail con i vostri dati , dopo le opportune verifiche inseriremo i vostri dati o in base alla vostra eventuale richiesta rimuoveremo il testo.
Parola chiave google : Compenetrazione di solidi tipo file : doc
Compenetrazione di solidi
Visita la nostra pagina principale
Compenetrazione di solidi
Termini d' uso e privacy