Sviluppi di solidi nel disegno tecnico

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Sviluppi di solidi nel disegno tecnico

Generalità

Una superficie si dice sviluppabile se può essere distesa su un piano senza distorsioni. Lo sviluppo di un solido consiste nell’aprire la sua superficie col minimo numero di tagli e nel distenderla su un piano.

La superficie piana risultante si chiama sviluppo della superficie.

Tutti i solidi delimitati da facce piane sono sviluppabili (figg. 3A e 3B).

Lo sviluppo esatto delle superfici curve è limitato a solidi delimitati da facce piane e da superfici a semplice curvatura come il cono o il cilindro (fig. 3C).

Figura 33 – Alcuni sviluppi di solidi elementari

Sviluppi approssimati, ma sufficientemente precisi, per certe applicazioni pratiche possono essere ottenuti per alcune superfici teoricamente non sviluppabili come quelle a doppia curvatura (ad esempio la sfera o un iperboloide).

Un’operazione di sviluppo è di fondamentale importanza per il progetto di tutte le opere di carpenteria metallica realizzate in lamiera, quali tubi, serbatoi o elementi di scafo. Altri esempi usuali di applicazioni dello sviluppo di superficie si hanno nelle fabbricazioni di scatole, di contenitori conici o cilindrici, nonché nello studio di pezzi imbutiti. Infatti, per la costruzione di tali elementi si parte da una lamiera piana che, con opportune lavorazioni, dovrà realizzare la forma desiderata.

E’ evidente quindi la necessità di conoscere lo sviluppo per il tracciamento sulla lamiera del contorno esatto della superficie da ritagliare.

Sviluppo di poliedri

Tutti gli sviluppi sono effettuati tenendo presente la regola generale che i lati della figura sviluppata e quelli corrispondenti del solido di origine devono avere la stessa lunghezza. Lo sviluppo di poliedri richiede il taglio lungo spigoli appropriati e la distensione sul piano; questo significa determinare la vera forma di tutte le facce che delimitano il poliedro e unire queste in sequenza lungo gli spigoli comuni.

La figura 34 indica la costruzione da seguire per la rappresentazione dello sviluppo di un parallelepipedo retto.

Figura 34 – Sviluppo della superficie di un parallelepipedo a base rettangolare eseguita col taglio lungo gli spigoli AD, DC, CB, DH, EH, HG, FG

Nella figura 35 il parallelepipedo è sezionato da un piano inclinato rispetto al p.o. e perpendicolare al p.v.. Poiché nella costruzione dello sviluppo gli spigoli dei solidi prismatici devono essere considerati nella loro grandezza reale, è opportuno far uso di una vista ausiliaria in modo che sia possibile misurare la vera grandezza di tutti gli spigoli.

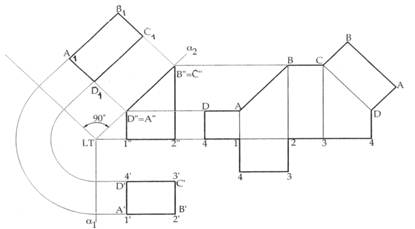
Una piramide consta di facce triangolari, tutte concorrenti nel vertice. Determinata quindi la vera forma delle facce laterali, si ottiene facilmente lo sviluppo della piramide, come in figura 36, o del tronco di piramide, come in figura 37.

Figura 36 - Sviluppo di una piramide retta a base quadrata; la superficie della piramide è composta da un quadrato e da quattro triangoli isosceli inclinati e col vertice in comune; per determinare la vera lunghezza dello spigolo della piramide è sufficiente ribaltare lo spigolo nel piano del disegno, centrando in V₁, con raggio V₁P₁, fino a determinare il punto P₁’. Questo punto, proiettato sul p.v., darà origine al punto P₂’, e il segmento V₂P₂’ determinerà cosi la reale lunghezza dello spigolo V₂P₂. Con raggio R corrispondente a tale lunghezza si descrive un arco di circonferenza e su di esso si riporta per 4 volte la corda corrispondente allo spigolo di base del solido

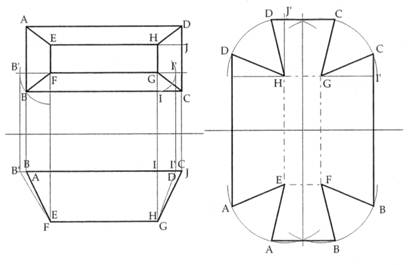
Figura 37 - Sviluppo di un tronco di piramide retta. Bisogna innanzi tutto ricavare le vere dimensioni di ogni elemento dello sviluppo: in questo caso l’operazione è resa più semplice dalla simmetria dell’oggetto. Con centro in F sul p.v. si ruota il segmento che rappresenta lo spigolo portando B in B’: il segmento FB’ nel p.o. rappresenta la vera lunghezza dello spigolo FB; gli altri segmenti paralleli al p.o. o al p.v. appaiono già in vera grandezza. Per trovare la vera forma del trapezio BCGF si ricorre alla linea ausiliaria GI: portando il segmento GI sul p.v. parallelo alla lt, si individua il punto I’ che consente sul p.o. la costruzione della vera lunghezza di GI (data dal segmento HI’). In modo analogo si ricava la lunghezza effettiva del segmento HJ. Immaginando quindi di tagliare la superficie secondo gli spigoli AE, BF, CG, DH e posizionando sul piano di sviluppo il rettangolo EFHG, con centro nei suoi vertici si tracciano archi di raggio FB’, che vengono intersecati dalle parallele ai lati del rettangolo da essi distanti rispettivamente GI’ e HJ’, ricavando in tal modo i vertici A, B, C e D

Si riporta, per completezza, un ulteriore esempio di sviluppo di un tronco di piramide esagonale retta ottenuto sezionando la piramide con un piano obliquo rispetto all’asse della piramide (fig. 38).

In figura 39 è mostrato lo sviluppo di una piramide obliqua, che rappresenta quindi un caso del tutto generale.

In questo caso conviene procedere, noti prospetto e pianta, costruendo lo sviluppo dell’intera piramide; individuato il taglio più breve, si procede poi sistematicamente fissando la lunghezza degli spigoli, con l’ausilio ancora di un diagramma di vere lunghezze.

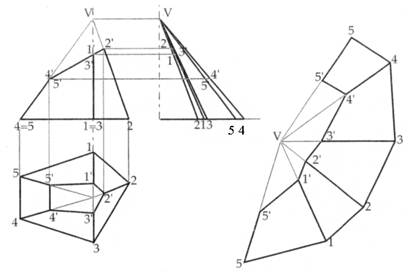
Ciò fatto, si è in grado di costruire i 5 triangoli 5V1,1V2, 2V3, 3V4, 4V5 in vera forma e nella

successione indicata. Poiché per regola lo sviluppo deve essere effettuato mediante tagli che abbiano la minore lunghezza possibile (ciò perché, nella costruzione, le superfici di sviluppo devono essere poi collegate lungo i tagli mediante saldatura, ecc.), il taglio sarà effettuato lungo lo spigolo V5, mentre per quanto riguarda la base, essa avrà in comune con la superficie laterale uno dei lati maggiori, cioè ad esempio il lato 3-4.

Per completare lo sviluppo, si individua il lato più lungo della base inferiore e questo sarà il lato in comune con la superficie laterale.

Per la base superiore, si deve prima ottenere una vista in vera forma e si procede poi come per la base superiore. Si noti che se la base superiore si sovrappone allo sviluppo della superficie laterale, si deve eventualmente rinunciare ad avere in comune il lato più lungo, poiché sovrapposizioni non sono evidentemente possibili. Se, comunque operando, la base superiore si sovrappone ancora alla superficie laterale, ne segue che lo sviluppo completo non è possibile (ovviamente il problema non si pone se il solido è aperto superiormente o limitato alla superfide laterale).

Un prisma può essere sviluppato rapidamente ricordando che una sezione, effettuata con un piano perpendicolare a tutti gli spigoli, taglia il prisma secondo una linea pure perpendicolare a tutti gli spigoli. Tale linea, detta perimetrale, ha lunghezza eguale al perimetro.

Se si dispone il prisma in modo da avere una vista (ad esempio la pianta) perpendicolare all’asse del

prisma, questa rappresenta in vera forma ogni sezione retta. Il perimetro è allora derivabile da tale vista. Sviluppando il prisma di fianco al prospetto, si determinano gli spigoli in vera lunghezza.

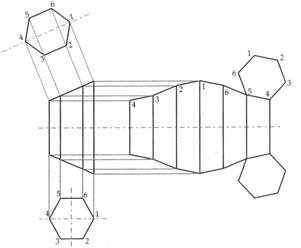La figura 40 mostra il caso di un prisma retto con basi oblique. Come sempre il taglio deve essere effettuato lungo lo spigolo più corto.

Figura 40 – Sviluppo di un prisma retto con basi oblique

Sviluppo di cilindri

Lo sviluppo di un cilindro retto, a sezione circolare, è semplicemente un rettangolo avente la base eguale al perimetro di base ed altezza eguale all'altezza del cilindro (fig. 41).

Figura 41 – Sviluppo di un cilindro retto

Se il cilindro è delimitato da una faccia obliqua (fig. 42), si può procedere ad una costruzione approssimata, dividendo la circonferenza di base del cilindro in n parti.

L’approssimazione è tanto maggiore quanto più numerose sono le divisioni della base.

Figura 42 - Prima di determinare lo sviluppo, si rappresenta la vera forma della faccia superiore; a tale scopo si divide la circonferenza di

base del cilindro ad esempio in 12 parti uguali e si riportano nella vista ausiliaria i segmenti BC, DE, ecc. uguali rispettivamente ai segmenti 2‑12, 3‑11, ecc., fino a costruire l’ellisse per punti. Il lato di base dello sviluppo della superficie, di lunghezza eguale a πd, viene diviso nello stesso numero di parti uguali e ad ogni divisione si innalza la generatrice corrispondente, che viene troncata con le corrispondenti proiezioni dal p.v.

La figura 43 mostra la costruzione per disegnare lo sviluppo di cilindri compenetrati, metodo che risulta utile per ricavare la forma in piano della lamiera per la costruzione di tubazioni con varie derivazioni. Per eseguire lo sviluppo di un innesto devono essere state già ricavate le curve di compenetrazione secondo i metodi già illustrati.

Figura 43 - Sviluppo di due cilindri perpendicolari di diverso diametro. La prima operazione da svolgere è quella di determinare con le regole viste la curva di intersezione sul p.v..

Per lo sviluppo del cilindro di diametro d, si riporta la lunghezza della circonferenza πd, si divide in 12 parti uguali e si riportano lungo le generatrici orizzontali i segmenti 1A₄, 2B₄, 3C₄, , 4D₄ uguali rispettivamente ai segmenti 1A₂, 2B₂, 3C₂, 4D₂ e si ritrova lo sviluppo ripetendo ciclicamente queste distanze. Lo sviluppo del cilindro di diametro D è un rettangolo con due fori ellittici che vengono determinati in modo approssimato: a partire dal centro dell’ellisse si riportano sull’asse maggiore le corde A₃B₃, uguale ad A₁B₁, B₃C₃, uguale a B₁C₁ e così via fino a costruire l’ellisse congiungendo i punti di incontro delle orizzontali da A₂ ecc. e le verticali da A₃ ecc..

Sviluppo

di coni

Un cono retto (o un tronco di cono retto a basi parallele) può essere sviluppato esattamente secondo un settore circolare avente raggio pari alla generatrice del cono (fig. 44).

L’angolo al vertice dello sviluppo è α = 360 r / l (gradi) o α = 2π r / l (radianti), dove r è il raggio del cerchio di base ed l la lunghezza della generatrice del cono.

Figura 44 – Sviluppo di un cono di raggio r avente generatrice di lunghezza l

La figura 45 illustra il metodo per ricavare lo sviluppo di un cono retto, tagliato da un piano non parallelo alla base.

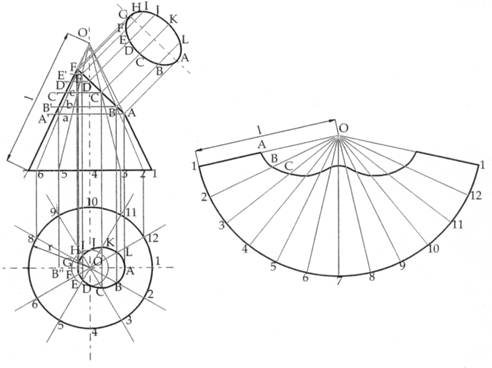
Figura 45 - Sviluppo di un cono tagliato con un piano non parallelo alla base. Innanzitutto si determina la proiezione della sezione sul p.o.. Utilizzando linee radiali equamente spaziate, la vista in pianta viene divisa in parti eguali che vengono ritrovate sul prospetto sotto forma di generatrici del cono. Utilizzando una serie di piani secanti orizzontali a, b, c, ... è possibile determinare sulla pianta i punti A, B, C, ... che le linee radiali intercettano a partire dai corrispondenti punti del prospetto, ottenendo la proiezione in pianta della figura ellittica di intersezione col piano. Lo sviluppo si ottiene riportando un arco di apertura 360 r / l (in gradi) e raggio l diviso nello stesso numero di parti del cono; su ogni linea radiale si riportano i segmenti 1A, 2B, ecc. in vera lunghezza (determinabile con il procedimento già ripetutamente visto), ottenendo lo sviluppo.

E’ possibile infine costruire la vera forma della sezione, tenendo presente che è ellittica, con l’asse maggiore uguale ad AG del prospetto e l’asse minore uguale al corrispondente asse minore dell’ellisse KC già disegnato in pianta.

Raccordi di condotte

In conclusione, viene illustrato un caso di sviluppo di un raccordo fra un condotto cilindrico ed uno prismatico, caso piuttosto frequente nella pratica. Questi pezzi vengono anche chiamati pezzi di transizione, in quanto da un estremo all'altro dell’asse del pezzo si ha un cambiamento della forma della sezione.

La figura 46 mostra il caso di un raccordo di un condotto prismatico con uno cilindrico, la cui superficie è costituita da quattro porzioni piane di forma triangolare e da quattro porzioni di superficie conica.

Figura 46 - Costruzione dello sviluppo di un pezzo di transizione: lo sviluppo si compone di quattro triangoli isosceli e di quattro superfici coniche. La linea di taglio è secondo ES. Si divide l’arco EF in un certo numero di parti uguali e si costruisce, nella vista principale, il diagramma delle vere lunghezze delle generatrici della superficie conica

Fonte: ftp://ftp.aula.dimet.unige.it/squarzoni/DTN1%202008.09%20-%20Cap.%2005%20Sezioni,%20intersezioni%20e%20sviluppi%20di%20solidi%20elementari.doc

Sito web da visitare: http://unige.it/

Autore del testo: non indicato nel documento di origine

Nota : se siete l'autore del testo sopra indicato inviateci un e-mail con i vostri dati , dopo le opportune verifiche inseriremo i vostri dati o in base alla vostra eventuale richiesta rimuoveremo il testo.

Sviluppi di solidi nel disegno tecnico