Superfici e solidi di rotazione geometria e disegno

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Superfici e solidi di rotazione geometria e disegno

Superfici e solidi di rotazione

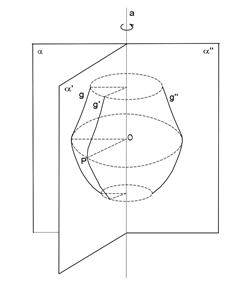a attorno ad a, g descrive una superficie.

Superficie di rotazione Þ superficie descritta da g.

Asse di rotazione Þ retta a.

Generatrice Þ linea g.

Un punto qualunque P di g descrive una circonferenza che giace in un piano perpendicolare all’asse di rotazione e il centro O sta sull’asse medesimo.

Paralleli Þ circonferenze descritte dai singoli punti di g nella rotazione.

Meridiani Þ insieme di due linee (g e g’’ ad esempio) diametralmente opposte rispetto all’asse a.

Solido di rotazione Þ solido ottenuto dalla rotazione di una superficie qualunque (es. poligono, cerchio, ecc. ) attorno ad una retta detta asse.

Cilindro

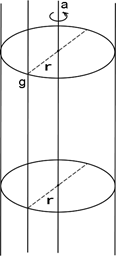
Superficie cilindrica di asse a Þ superficie ottenuta dalla rotazione di una retta g, parallela alla retta a, attorno alla retta a.

La superficie cilindrica è il luogo dei punti dello spazio la cui distanza da una retta fissa è costante.

Raggio Þ distanza costante tra le rette g ed a.

I paralleli di una superficie cilindrica sono circonferenze uguali aventi per raggio il raggio della superficie; i meridiani sono coppie di rette parallele ad una distanza uguale al doppio del raggio.

Cilindro indefinito Þ solido costituito dall’insieme di punti di una superficie cilindrica e dai suoi punti interni (cioè i punti la cui distanza dall’asse a è minore del raggio)

. Il cilindro indefinito può pensarsi generato dalla rotazione della striscia ag attorno ad uno dei suoi lati.

Cilindro circolare retto Þ insieme dei punti che appartengono contemporaneamente ad un cilindro indefinito e allo strato compreso tra due piani perpendicolari all’asse.

Il cilindro circolare retto può pensarsi generato da una rotazione completa di un rettangolo attorno a uno dei suoi lati oppure da una rotazione di un angolo piatto attorno ad un suo asse di simmetria.

Basi del cilindro Þ sono due cerchi uguali ottenuti dall’intersezione del cilindro indefinito con i due piani secanti.

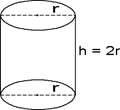superficie cilindrica compresa tra i due piani secanti.

Superficie totale del cilindro Þ insieme della superficie laterale e delle due basi.

Altezza del cilindro Þ distanza tra le due basi.

cilindro la cui altezza è uguale al diametro di base: la sua sezione piana passante per l’asse è un quadrato.

Cono

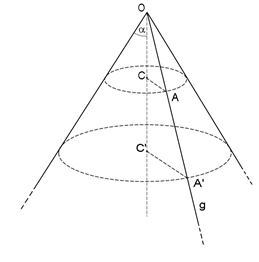
Superficie conica Þ superficie ottenuta dalla rotazione completa di una semiretta g di origine O attorno ad una retta a passante per O (Il punto O è detto vertice).

Teorema 35 – I raggi dei paralleli di una superficie conica sono proporzionali sia alla distanza dei piani corrispondenti dal vertice, sia alla distanza dei punti dei paralleli dal vertice stesso.

Ts: CA : C’A’ = OC : OC’ CA : C’A’ = OA : OA’

La superficie conica può pensarsi come luogo delle semirette uscenti da uno stesso punto O di una retta (asse) formanti con essa un angolo costante a detto semiapertura della superficie.

Cono indefinito Þ solido costituito dall’insieme di tutti i punti di una superficie conica e dai suoi punti interni.

Il cono indefinito si può pensare generato dalla rotazione completa di un angolo attorno ad uno dei suoi lati.

Teorema 36 – Le sezioni di un cono con i piani perpendicolari all’asse sono cerchi le cui aree sono proporzionali ai quadrati delle rispettive distanze dal vertice.

Ts: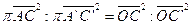

insieme di punti di un cono indefinito compresi tra il suo vertice e un piano perpendicolare al suo asse che taglia il cono indefinito stesso.

Il cono circolare retto può pensarsi generato dalla rotazione completa di un triangolo rettangolo attorno ad un suo cateto.

Base del cono Þ Cerchio intersezione del cono indefinito con il piano a.

Raggio del cono Þ Raggio della sua base (AH).

Altezza del cono Þ Distanza del vertice dalla base (OH).

Apotema del cono Þ Segmento di generatrice compreso tra il vertice e la base (OA).

L’apotema del cono è l’ipotenusa di un triangolo rettangolo i cui cateti sono l’altezza del cono e il suo raggio di base.

Cono avente l’apotema uguale al diametro di base. La sezione con un piano passante per l’asse di un cono equilatero è un triangolo equilatero.

Tronco di cono

E’ la parte di cono circolare retto compreso tra la sua base e un piano a ad essa parallelo e secante il cono.

Il tronco di cono si può pensare generato dalla rotazione di un trapezio rettangolo attorno al lato perpendicolare alle basi.

Altezza del tronco Þ Distanza tra le sue basi (HH’).

Apotema del tronco Þ Parte di apotema del cono compreso tra le basi (AA’)

Sfera

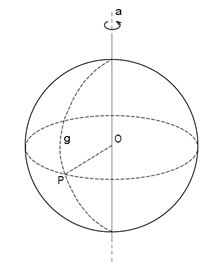
Superficie sferica Þ figura generata dalla rotazione completa di una semicirconferenza g attorno alla retta del suo diametro.

La superficie sferica è il luogo dei punti dello spazio equidistanti da un punto fisso detto centro.

Distanza di un qualunque suo punto dal centro.

I meridiani di una superficie sferica sono circonferenze aventi il centro e il raggio della superficie stessa.

I paralleli di una superficie sferica sono circonferenze aventi centro sull’asse di rotazione. Il parallelo massimo detto equatore ha il centro e il raggio della superficie sferica.

Teorema 37 – Una superficie sferica è rotonda rispetto ad un qualsiasi suo diametro.

Sfera Þ Solido formato dai punti di una superficie sferica e dai suoi punti interni (distanza dal centro minore del raggio).

Una sfera si può pensare generata dalla rotazione di un semicerchio attorno alla retta del suo diametro.

Parti della sfera

Fig. 1

ciascuna parte in cui la superficie sferica viene divisa da un piano secante.

Segmento sferico a 1 base Þ ciascuna parte in cui la sfera viene divisa da un piano secante.

Fig. 2

Zona sferica Þ parte di superficie sferica compresa tra due piani paralleli che tagliano la superficie.

Segmento sferico a 2 basi Þ parte di sfera compresa tra due piani secanti paralleli.

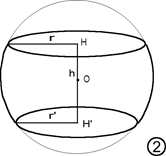
Settore sferico Þ parte di sfera generata dalla rotazione di un settore circolare attorno ad un diametro che giace nel piano del settore ma non lo attraversa.

Fig. 3 Þ settore sferico in cui la rotazione avviene intorno ad uno dei raggi che limitano il settore circolare.

Fig. 4 Þ settore sferico in cui l’asse di rotazione non contiene i raggi che limitano il settore circolare.

Fig. 5 Þ settore sferico in cui l’asse di rotazione non contiene i raggi che limitano il settore circolare.

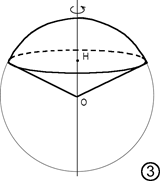
Fig. 6

Fuso sferico Þ parte di superficie sferica limitata da due piani diametrali (passanti per uno stesso diametro).

Spicchio sferico Þ parte di sfera limitata da un fuso e da due semicerchi massimi che si dicono facce dello spicchio. Il fuso si dice base dello spicchio.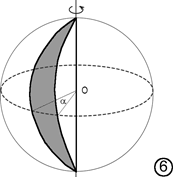

Fonte: http://4classd.wikispaces.com/file/view/Geometria_4.doc

Sito web da visitare: http://4classd.wikispaces.com

Autore del testo: non indicato nel documento di origine

Nota : se siete l'autore del testo sopra indicato inviateci un e-mail con i vostri dati , dopo le opportune verifiche inseriremo i vostri dati o in base alla vostra eventuale richiesta rimuoveremo il testo.

Parola chiave google : Superfici e solidi di rotazione geometria e disegno tipo file : doc

Superfici e solidi di rotazione geometria e disegno