Metallurgia riassunti
Metallurgia riassunti
Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.
Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).
Metallurgia riassunti
RIASSUNTI
- Descrivere il fattore di compattazione atomica delle principali strutture cristallografiche dei materiali metallici.
Il fattore di compattazione atomica (APF) rappresenta il volume degli atomi contenuti in una cella reticolare rispetto al volume totale della cella stessa, quindi: 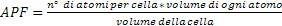 . Può essere studiato utilizzando il modello a sfere rigide, che considera ogni atomo come fosse appunto una sfera perfetta e rigida.
. Può essere studiato utilizzando il modello a sfere rigide, che considera ogni atomo come fosse appunto una sfera perfetta e rigida.
Le principali strutture cristallografiche dei materiali metallici sono:
- Cubica a corpo centrato (CCC o BCC), in cui la cella unitaria è cubica e presenta 8 atomi agli angoli e un singolo atomo al centro del cubo. I metalli più comuni che cristallizzano in questa struttura sono: Cr, Fe-α, Mo, K, Na, W, V, Ti-β. Il numero di coordinazione di questa struttura è 8 (partendo da qualsiasi punto del reticolo e spostandosi di una distanza interatomica nelle tre direzioni dello spazio vi sono altri 8 atomi). Poiché gli atomi agli angoli e quello centrale si toccano lungo la diagonale del cubo, indicando con a il suo spigolo, lungo la diagonale (
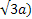 . Inoltre, nel sistema CCC ciascuna cella unitaria contiene 2 atomi: 1/8 di atomo per ognuno degli 8 atomi agli angoli (1 atomo in tutto) e un atomo centrale. L’APF sarà quindi dato da:
. Inoltre, nel sistema CCC ciascuna cella unitaria contiene 2 atomi: 1/8 di atomo per ognuno degli 8 atomi agli angoli (1 atomo in tutto) e un atomo centrale. L’APF sarà quindi dato da:
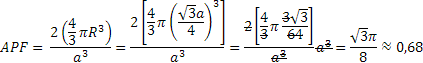
- Cubica a facce centrate (CFC o FCC), in cui la cella unitaria è cubica e presenta, oltre agli 8 atomi agli angoli, altri 6 atomi al centro di ogni faccia del cubo. Cristallizzano in questa struttura Ag, Au, Al, Cu, Pb, Ni, Fe-γ. Il numero di coordinazione è 12, e gli atomi si toccano lungo la diagonale di ciascuna faccia (lunga
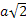 . Inoltre, in questo sistema cristallografico ciascuna cella unitaria contiene 4 atomi: come prima, 1/8 di atomo per ognuno degli 8 atomi agli angoli (1 atomo in tutto) e ½ atomo per ognuno dei 6 atomi al centro delle facce del cubo (3 atomi in tutto). Il fattore di compattazione atomica sarà allora:
. Inoltre, in questo sistema cristallografico ciascuna cella unitaria contiene 4 atomi: come prima, 1/8 di atomo per ognuno degli 8 atomi agli angoli (1 atomo in tutto) e ½ atomo per ognuno dei 6 atomi al centro delle facce del cubo (3 atomi in tutto). Il fattore di compattazione atomica sarà allora:
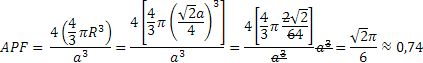
- Esagonale compatta (EC o HCP), a simmetria esagonale, delimitata da due facce (ciascuna delle quali ospita 6 atomi agli angoli e un atomo al centro), fra le quali vi è un piano intermedio che ospita altri 3 atomi, analogo a quelli basali ma traslato rispetto ad essi. Cristallizzano in una struttura del genere Zn, Mg, Co, Cd, Zr, Ti-α, Be. Il numero di coordinazione è 12. I sei atomi sui piani basali si toccano fra loro, per cui
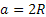 . Nel sistema HCP ciascuna cella contiene 6 atomi: 1/6 di atomo per ciascuno dei 12 atomi sui piani basali (2 atomi in tutto), ½ atomo per i due atomi centrali sui piani basali (1 atomo in tutto) e tre atomi sul piano intermedio. Per cui infine si ha che:
. Nel sistema HCP ciascuna cella contiene 6 atomi: 1/6 di atomo per ciascuno dei 12 atomi sui piani basali (2 atomi in tutto), ½ atomo per i due atomi centrali sui piani basali (1 atomo in tutto) e tre atomi sul piano intermedio. Per cui infine si ha che:
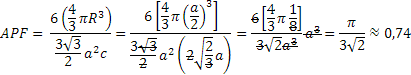
Da cui risulta che le strutture a maggior impacchettamento sono la cubica a facce centrate e l’esagonale.
( Conoscendo la struttura cristallografica è possibile calcolare la densità teorica di un metallo tramite la relazione: 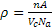 , con Na n° di Avogadro, n n° di atomi contenuti nella cella, Vc volume della cella, A peso atomico.)
, con Na n° di Avogadro, n n° di atomi contenuti nella cella, Vc volume della cella, A peso atomico.)
- Descrivere il meccanismo di Frank-Read.
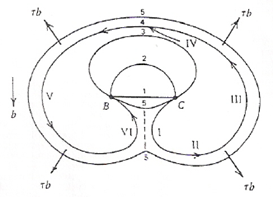
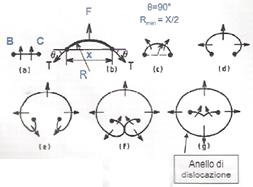
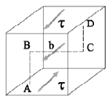
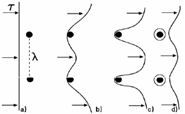
Il meccanismo di Frank-Read rappresenta uno dei principali metodi tramite cui le dislocazioni si moltiplicano. Si consideri, ad esempio, un cristallo cubico che presenta tre dislocazioni a spigolo, indicate dai segmenti AB, BC e CD, sottoposto ad una tensione di taglio τ. Le dislocazioni indicate dai segmenti AB e CD non potranno muoversi, in quanto il loro vettore di Burgers è perpendicolare alla direzione di movimento; in conseguenza di ciò nemmeno la dislocazione BC, avendo gli estremi fissati, potrà muoversi, per cui tenderà ad incurvarsi. Ponendo uguale ad x la distanza fra i due estremi B e C, il segmento di dislocazione si curva fino a quando la forza F applicata sulla linea di dislocazione non eguaglia la tensione di linea T (definita come il lavoro necessario a generare una unità di lunghezza della linea di dislocazione), per cui all’equilibrio risulterà: 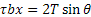 , valore che fornisce una buona approssimazione per la tensione di linea T. Il segmento continua quindi ad espandersi e curvarsi (passaggi 1, 2, 3 e 4). Ciò accade perché il segmento b è sempre lo stesso e la forza sulla linea τb agisce sempre ad angoli retti, tendendo ad ampliare il circuito della dislocazione; infatti:
, valore che fornisce una buona approssimazione per la tensione di linea T. Il segmento continua quindi ad espandersi e curvarsi (passaggi 1, 2, 3 e 4). Ciò accade perché il segmento b è sempre lo stesso e la forza sulla linea τb agisce sempre ad angoli retti, tendendo ad ampliare il circuito della dislocazione; infatti:
- nei punti IV e II la dislocazione è pura di taglio con il piano extra al di sotto del piano di scorrimento in IV e al di sopra in II, per cui questi due segmenti, essendo di segno opposto, tendono ad allontanarsi uno dall’altro;
- nei punti I, III, V e VI la dislocazione è pura a vite (sinistrorsa in I e V e destrorsa in III e VI), per cui i segmenti I e VI, essendo di segno opposto, si muovono in direzioni opposte, incontrandosi, collassando lungo la loro intersezione, e facendo quindi rompere la linea in due parti.
- Descrivere il meccanismo di Frank-Read.
Il meccanismo di Frank-Read rappresenta uno dei principali metodi tramite cui le dislocazioni si moltiplicano. Si consideri, ad esempio, un cristallo cubico che presenta tre dislocazioni a spigolo, indicate dai segmenti AB, BC e CD, sottoposto ad una tensione di taglio τ. Le dislocazioni indicate dai segmenti AB e CD non potranno muoversi, in quanto il loro vettore di Burgers è perpendicolare alla direzione di movimento; in conseguenza di ciò nemmeno la dislocazione BC, avendo gli estremi fissati, potrà muoversi, per cui tenderà ad incurvarsi. Ponendo uguale ad x la distanza fra i due estremi B e C, il segmento di dislocazione si curva fino a quando la forza F applicata sulla linea di dislocazione non eguaglia la tensione di linea T (definita come il lavoro necessario a generare una unità di lunghezza della linea di dislocazione), per cui all’equilibrio risulterà: 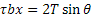 , valore che fornisce una buona approssimazione per la tensione di linea T. Il segmento continua quindi ad espandersi e curvarsi (passaggi 1, 2, 3 e 4). Ciò accade perché il segmento b è sempre lo stesso e la forza sulla linea τb agisce sempre ad angoli retti, tendendo ad ampliare il circuito della dislocazione; infatti:
, valore che fornisce una buona approssimazione per la tensione di linea T. Il segmento continua quindi ad espandersi e curvarsi (passaggi 1, 2, 3 e 4). Ciò accade perché il segmento b è sempre lo stesso e la forza sulla linea τb agisce sempre ad angoli retti, tendendo ad ampliare il circuito della dislocazione; infatti:
- nei punti IV e II la dislocazione è pura di taglio con il piano extra al di sotto del piano di scorrimento in IV e al di sopra in II, per cui questi due segmenti, essendo di segno opposto, tendono ad allontanarsi uno dall’altro;
- nei punti I, III, V e VI la dislocazione è pura a vite (sinistrorsa in I e V e destrorsa in III e VI), per cui i segmenti I e VI, essendo di segno opposto, si muovono in direzioni opposte, incontrandosi, collassando lungo la loro intersezione, e facendo quindi rompere la linea in due parti.
 .
.
- Descrivere la cinetica di cristallizzazione in atto durante la solidificazione di un metallo.
La cinetica di cristallizzazione comprende due fasi:
- Nucleazione, che si può distinguere in:
- nucleazione omogenea, più rara in quanto avviene quando i germi cristallini si formano in modo omogeneo all'intero del fuso e in modo uniforme in tutte le direzioni, e richiede un notevole sottoraffreddamento (centinaia di °C);
- nucleazione eterogenea, più frequente poiché necessita di un grado di sottoraffreddamento molto minore per formare un nucleo stabile: questo processo si serve infatti di agenti nucleanti, sui quali la nucleazione avviene più facilmente, in quanto l’energia di superficie necessaria per formare un nucleo stabile è più bassa su questo materiale rispetto a quella che sarebbe necessaria se il nucleo si formasse nel liquido puro. Questi agenti possono essere frammenti della stessa sostanza cristallina in precedenza non completamente fusi o volutamente aggiunti, inclusioni di particelle estranee, particolari posizioni della superficie del liquido o le pareti del contenitore.
- Accrescimento dei grani, per cui i nuclei si accrescono formando cristalli, in cui gli atomi sono disposti in modo essenzialmente regolare, ma varia l’orientazione di ogni cristallo. Quando la solidificazione del metallo è completata, i cristalli si uniscono tra loro pur se con diverse orientazioni, formando legami fra i grani limitati ad un certo numero di atomi. Il metallo solidificato che contiene molti cristalli è detto policristallino; i cristalli nel metallo solidificato sono chiamati grani, e le superfici tra loro bordi di grano. Il numero di siti di nucleazione che si creano in un metallo che solidifica influenza la struttura dei grani del metallo solido: se si creano pochi siti si formerà una struttura a grani grossi, mentre se si hanno molti siti di nucleazione si formerà una struttura a grani fini, la quale determina migliori proprietà di resistenza meccanica e di uniformità dei prodotti finiti.
Per ottenere strutture monocristalline la solidificazione deve avvenire attorno ad un singolo nucleo, quindi la T di interfaccia deve essere solo di poco < del punto di fusione del solido e la T del liquido deve aumentare all’interfaccia. Questo gradiente di T può essere ottenuto facendo in modo che il calore latente di solidificazione (energia rilasciata quando un metallo solidifica) fluisca lungo il cristallo in fase di solidificazione; inoltre la velocità di crescita del cristallo deve essere bassa, così che la T all’interfaccia liquido-solido sia di poco < del punto di fusione del solido.
( 1): Si possono definire anche la velocità di nucleazione, ossia il numero di germi stabili per unità di volume e di tempo [m-3 s-1], che aumenta considerevolmente con il grado di sottoraffreddamento, e la frequenza di nucleazione, il numero di nuclei per unità di volume in grado di accrescersi, ossia il numero di embrioni che raggiungono le dimensioni critiche diventando nuclei. )
- Descrivere gli indici di Miller e Miller-Bravais.
Gli indici di Miller (hkl) caratterizzano una sequenza di piani paralleli all’interno di un reticolo, in tutti i sistemi tranne quello esagonale, e rappresentano i reciproci delle intercette che i piani individuano con gli assi cristallografici. Si calcolano quindi in questo modo:
- se il piano passa per l’origine, lo si deve traslare, mantenendo ovviamente il parallelismo;
- il piano così ottenuto interseca gli assi o ne è parallelo; l’intercetta viene quantificata in termini di parametri reticolari a, b e c;
- si calcolano i reciproci di tali numeri (se il piano è // ad uno degli assi: intercetta = ∞ à reciproco =
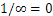 );
); - i numeri così ottenuti devono essere trasformati nei più piccoli interi utilizzando un fattore comune;
- i tre indici così ottenuti vengono racchiusi fra parentesi tonde.
Poiché si possono avere anche intercette sugli assi negative, gli indici possono assumere anche valori negativi (indicati da una barretta sopra l’indice).
Per fare in modo che anche nei cristalli a simmetria esagonale direzioni e piani equivalenti abbiano gli stessi indici si fa ricorso al sistema di coordinate di Miller-Bravais, a quattro assi: i tre assi a1, a2 ed a3 sono contenuti nello stesso piano, con angoli di 120° fra loro, mentre l’asse z è perpendicolare al piano formato dagli altri tre.
Le direzioni, in questo sistema, sono identificate dagli indici [uvtw], essendo i primi tre indici le proiezioni del vettore considerato sui tre assi del piano di base. La conversione fra gli indici del sistema a tre assi [u’v’w’] e quello a quattro assi [uvtw] (con n fattore necessario a portare tutti gli indici al più piccolo valore intero) avviene secondo le relazioni:
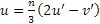
Gli indici di Miller-Bravais (hkil), caratterizzano una sequenza di piani paralleli nei sistemi esagonali: si ottengono trovando il reciproco delle intercette con i quattro assi a1, a2, a3 e z, e riducendo queste ai più piccoli interi. L’indice i si ricava tramite la relazione: 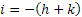 ; h, k e l corrispondono a quelli che si trovano nel sistema a tre assi.
; h, k e l corrispondono a quelli che si trovano nel sistema a tre assi.
 - Descrivere il meccanismo di Orowan e il meccanismo di taglio.
- Descrivere il meccanismo di Orowan e il meccanismo di taglio.
 . Questa relazione suggerisce che per avere materiali di elevata resistenza è necessario che le particelle di seconda fase siano fittamente distribuite, in modo che la spaziatura interparticellare λ sia minima (è quindi preferibile avere molte piccole particelle piuttosto che poche particelle grossolane).
. Questa relazione suggerisce che per avere materiali di elevata resistenza è necessario che le particelle di seconda fase siano fittamente distribuite, in modo che la spaziatura interparticellare λ sia minima (è quindi preferibile avere molte piccole particelle piuttosto che poche particelle grossolane).
Il meccanismo di taglio interviene quando una dislocazione, per superare le particelle che ne ostacolano il movimento, le taglia. Ciò può accadere solo se i piani atomici di scorrimento nella matrice e nella particella coincidono. Detto r il raggio della particella, si ha che in generale: 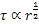 . In questo caso, quindi, il meccanismo diventa più efficace man mano che le particelle crescono.
. In questo caso, quindi, il meccanismo diventa più efficace man mano che le particelle crescono.
È chiaro che i due meccanismi coesistono, ma a permettere di volta in volta il superamento dell’ostacolo è il più efficiente (quello che richiede tensioni minori).
- Descrivere la trasformazione eutettica.
Si ha una trasformazione eutettica quando una lega di composizione eutettica viene raffreddata lentamente al di sotto della temperatura eutettica (temperatura più bassa di esistenza della fase liquida durante un raffreddamento lento), per cui il liquido monofase si trasforma simultaneamente in due fasi solide (soluzioni solide α e β); in forma generale può essere scritta come: liquido à(raffreddamento)àα + β.
 Tale trasformazione è detta invariante perché avviene in condizioni di equilibrio ad una specifica temperatura e composizione di lega che non possono essere variate: composizione e temperatura eutettica, infatti, determinano un punto eutettico sul diagramma di stato, in cui la fase liquida è in equilibrio con le due soluzioni solide α e β, e quindi coesistono tre fasi di equilibrio. Poiché in un diagramma di stato binario quando sono presenti tre fasi la varianza è pari a 2+1-3=0 (zero gradi di libertà, F+V=C+1), alla temperatura eutettica si ha un arresto termico nella curva di raffreddamento di una lega di composizione eutettica.
Tale trasformazione è detta invariante perché avviene in condizioni di equilibrio ad una specifica temperatura e composizione di lega che non possono essere variate: composizione e temperatura eutettica, infatti, determinano un punto eutettico sul diagramma di stato, in cui la fase liquida è in equilibrio con le due soluzioni solide α e β, e quindi coesistono tre fasi di equilibrio. Poiché in un diagramma di stato binario quando sono presenti tre fasi la varianza è pari a 2+1-3=0 (zero gradi di libertà, F+V=C+1), alla temperatura eutettica si ha un arresto termico nella curva di raffreddamento di una lega di composizione eutettica.
Ad esempio, nella lega Pb-Sn, sono presenti due regioni di limitata solubilità solida alle due estremità del diagramma, definite soluzioni solide limite: la fase α, soluzione solida ricca di Pb in cui può disciogliersi un massimo del 19,2% di Sn a 183 °C (temperatura eutettica), e la fase β, soluzione solida ricca di Sn in cui può disciogliersi un massimo del 2,5% di Pb alla stessa temperatura. Composizione eutettica: 61,9%Sn-38,1%Pb.
- Descrivere la trasformazione peritettica.
Nella trasformazione peritettica una fase liquida interagisce con una fase solida per formare una nuova fase solida, diversa dalla precedente; in forma generale può essere scritta come: liquido + α à(raffreddamento)àβ. Questa trasformazione, quindi, avviene quando una lega di composizione peritettica viene raffreddata lentamente al di sotto della temperatura peritettica.
 γ (4,3%Ni).
γ (4,3%Ni).
Da notare che, se una lega ha meno di 4,3%Ni ed è raffreddata lentamente dallo stato liquido attraverso la regione liquido + δ, si avrà un eccesso di fase δ una volta che la trasformazione peritettica è completata; allo stesso modo, se una lega Fe-Ni con più di 4,3%Ni, ma meno di 5,4%Ni, è raffreddata lentamente, passando dallo stato liquido attraverso la regione bifasica δ + liquido, ci sarà un eccesso di fase liquida dopo che la trasformazione è completata.
- Descrivere la legge di Fick in condizioni stazionarie (I legge di Fick).
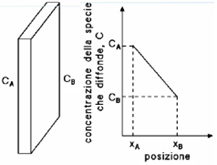 . La costante D è detta diffusività o coefficiente di diffusione [m2/s], e dipende da temperatura e tipo di meccanismo di diffusione (sostituzionale o interstiziale), struttura cristallina del mezzo di diffusione (ferro CCC: 10-12 m2/s, ferro CFC: 10-15 m2/s), tipo di difetti cristallini (aumenta in corrispondenza di vacanze e bordi di grano), concentrazione delle specie diffuse. La legge di Fick indica molto chiaramente che i fenomeni diffusivi avvengono in direzione opposta rispetto al gradiente di concentrazione, per cui questo va a costituire la driving force del processo diffusivo.
. La costante D è detta diffusività o coefficiente di diffusione [m2/s], e dipende da temperatura e tipo di meccanismo di diffusione (sostituzionale o interstiziale), struttura cristallina del mezzo di diffusione (ferro CCC: 10-12 m2/s, ferro CFC: 10-15 m2/s), tipo di difetti cristallini (aumenta in corrispondenza di vacanze e bordi di grano), concentrazione delle specie diffuse. La legge di Fick indica molto chiaramente che i fenomeni diffusivi avvengono in direzione opposta rispetto al gradiente di concentrazione, per cui questo va a costituire la driving force del processo diffusivo.
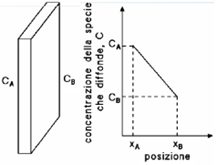
Considerando ad esempio una lamiera che divide due gas a concentrazioni costanti CA e CB, con CA > CB, riportando la concentrazione in funzione della posizione all’interno dello spessore della lastra, si ottiene una curva detta profilo di concentrazione. La pendenza della curva, in un determinato punto, è il gradiente di concentrazione, definito come 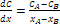 .
.
 .
.
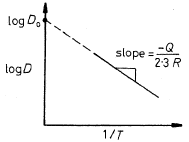
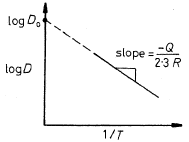
- La diffusività D rappresenta la facilità con cui una data specie atomica diffonde in un’altra, e dipende notevolmente dalla temperatura, tramite la relazione nella forma di Arrhenius: (*)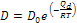 , in cui D0 [m2/s] è una costante che non dipende dalla temperatura nell’intervallo in cui l’equazione è valida, Qd è l’energia (entalpia) di attivazione per le specie che diffondono, R è la costante molare dei gas e T la temperatura assoluta, in K.
, in cui D0 [m2/s] è una costante che non dipende dalla temperatura nell’intervallo in cui l’equazione è valida, Qd è l’energia (entalpia) di attivazione per le specie che diffondono, R è la costante molare dei gas e T la temperatura assoluta, in K.
L’equazione può essere scritta anche in forma logaritmica come equazione di una retta: 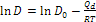 . )
. )
( (*) Se un atomo sta vibrando con frequenza ν in direzione x, esso sta compiendo ν tentativi di salto al secondo per passare al sito vicino, e la frazione di tentativi che hanno successo è 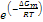 )
)
Descrivere la legge di Fick in condizioni stazionarie (I legge di Fick).
 . La costante D è detta diffusività o coefficiente di diffusione [m2/s], e dipende da temperatura e tipo di meccanismo di diffusione (sostituzionale o interstiziale), struttura cristallina del mezzo di diffusione (ferro CCC: 10-12 m2/s, ferro CFC: 10-15 m2/s), tipo di difetti cristallini (aumenta in corrispondenza di vacanze e bordi di grano), concentrazione delle specie diffuse. La legge di Fick indica molto chiaramente che i fenomeni diffusivi avvengono in direzione opposta rispetto al gradiente di concentrazione, per cui questo va a costituire la driving force del processo diffusivo.
. La costante D è detta diffusività o coefficiente di diffusione [m2/s], e dipende da temperatura e tipo di meccanismo di diffusione (sostituzionale o interstiziale), struttura cristallina del mezzo di diffusione (ferro CCC: 10-12 m2/s, ferro CFC: 10-15 m2/s), tipo di difetti cristallini (aumenta in corrispondenza di vacanze e bordi di grano), concentrazione delle specie diffuse. La legge di Fick indica molto chiaramente che i fenomeni diffusivi avvengono in direzione opposta rispetto al gradiente di concentrazione, per cui questo va a costituire la driving force del processo diffusivo.
Considerando ad esempio una lamiera che divide due gas a concentrazioni costanti CA e CB, con CA > CB, riportando la concentrazione in funzione della posizione all’interno dello spessore della lastra, si ottiene una curva detta profilo di concentrazione. La pendenza della curva, in un determinato punto, è il gradiente di concentrazione, definito come 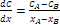 .
.
 .
.
- La diffusività D rappresenta la facilità con cui una data specie atomica diffonde in un’altra, e dipende notevolmente dalla temperatura, tramite la relazione nella forma di Arrhenius: (*)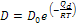 , in cui D0 [m2/s] è una costante che non dipende dalla temperatura nell’intervallo in cui l’equazione è valida, Qd è l’energia (entalpia) di attivazione per le specie che diffondono, R è la costante molare dei gas e T la temperatura assoluta, in K.
, in cui D0 [m2/s] è una costante che non dipende dalla temperatura nell’intervallo in cui l’equazione è valida, Qd è l’energia (entalpia) di attivazione per le specie che diffondono, R è la costante molare dei gas e T la temperatura assoluta, in K.
L’equazione può essere scritta anche in forma logaritmica come equazione di una retta: 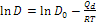 . )
. )
( (*) Se un atomo sta vibrando con frequenza ν in direzione x, esso sta compiendo ν tentativi di salto al secondo per passare al sito vicino, e la frazione di tentativi che hanno successo è 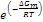 )
)
- Descrivere la legge di Fick in condizioni non-stazionarie (II legge di Fick).
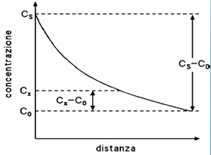
La risoluzione di questa equazione è possibile imponendo delle condizioni al contorno; un esempio ne è il caso del solido semi-infinito, nel quale nessun atomo della specie che diffonde è in grado di raggiungere l’estremità opposta nei tempi del processo: prima che la diffusione abbia inizio, la specie che diffonde si trova uniformemente distribuita nel solido ad una concentrazione C0: il valore di x è 0 sulla superficie del solido, ed aumenta man mano che ci si addentra nel solido stesso, mentre il tempo t=0 è quello in cui inizia la diffusione.
Per t=0: C=C0 per 0<x<∞; Per t>0: C=CS=costante per x=0, C=C0 per x=∞.
L’equazione può quindi essere risolta, e la soluzione è: 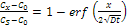
La funzione erf(z) è la funzione di errore Gaussiana, i cui valori sono tabulati in funzione della variabile z. Conoscendo i valori di D, C0 e CS, si può ricavare l’andamento della concentrazione in dei determinati posizione e tempo.
((*) Si considera una sottile porzione di materiale con area A e spessore δx. Il n° di atomi interstiziali che in un intervallo δt diffondono nella porzione attraverso il piano 1 è J1Aδt, mentre lasciano la porzione attraverso il piano 2 J2Aδt atomi; se J2<J1 la concentrazione di B all’interno della porzione Aδx sarà variata di (J1-J2)Aδt/(Aδx)=δCB. Poiché δxà0 e J2=J1+(δJ/δx)δx e δtà0 si ottiene che: δCB/δt=-δJB/δx. Inserendo la I legge di Fick si ha la (*). (c.v.d). )
-  Descrivere i difetti di linea.
Descrivere i difetti di linea.
Si distinguono due tipologie differenti di difetti di tipo lineare, o dislocazioni:
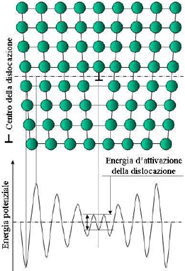
- Dislocazioni a spigolo o di taglio, rappresentabile tramite un semipiano addizionale di atomi in un reticolo, la cui estremità definisce una linea (il difetto), intorno al quale gli atomi sono spostati rispetto alla loro posizione ideale.
In una dislocazione a spigolo i filari adiacenti alla dislocazione sono deformati per un certo numero di piani atomici, fino a quando gli atomi ritornano alla corretta distanza reticolare, in cui l'energia dell'atomo è minima. Al centro della dislocazione esiste una buca d'energia potenziale, non occupata da alcun atomo. In tale situazione gli atomi nei pressi della dislocazione, per compiere uno slittamento d'un passo reticolare devono superare un gradino d'energia di attivazione molto più basso di quello degli atomi lontani dalla dislocazione o nel cristallo perfetto.
Si indica con il simbolo ┴ se il semipiano addizionale si trova al di sopra del piano di scorrimento (dislocazione positiva), e con T se si trova al di sotto (disloc. negativa).
In questo caso il vettore di Burger e la linea della dislocazione sono perpendicolari, per cui definiscono univocamente un piano di scorrimento, su cui la dislocazione è costretta a muoversi secondo un moto conservativo di glide, che causa solo un riaggiustamento di atomi; si ha invece un moto non conservativo di climb se la dislocazione si muove in direzione perpendicolare al vettore di Burger, tramite diffusione di atomi e vacanze (per temperature alte).
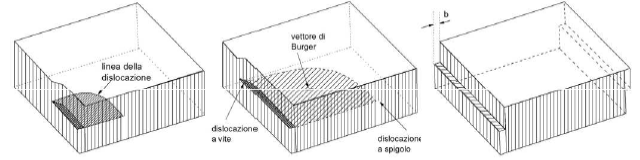
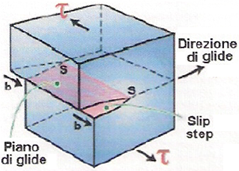 Dislocazioni a vite, generata applicando una tensione di taglio al reticolo cristallino, in modo da farne scorrere solo una parte, e causando quindi una distorsione localizzata intorno ad una linea. Tale nome deriva dal percorso elicoidale descritto intorno alla dislocazione dagli atomi dei piani adiacenti. In questo caso il vettore di Burger e la linea della dislocazione sono paralleli, per cui non è possibile definire un piano di scorrimento in modo univoco: tutti i piani del fascio aventi per asse la linea della dislocazione (e quindi il vettore di Burger) sono piani di scorrimento su cui la dislocazione può muoversi. Da ciò deriva la maggior mobilità di queste dislocazioni rispetto a quelle a spigolo. La dislocazione è detta a vite destrogira se il vettore di Burger ha verso discorde da quello della linea di dislocazione, a vite levogira se il vettore ha verso concorde.
Dislocazioni a vite, generata applicando una tensione di taglio al reticolo cristallino, in modo da farne scorrere solo una parte, e causando quindi una distorsione localizzata intorno ad una linea. Tale nome deriva dal percorso elicoidale descritto intorno alla dislocazione dagli atomi dei piani adiacenti. In questo caso il vettore di Burger e la linea della dislocazione sono paralleli, per cui non è possibile definire un piano di scorrimento in modo univoco: tutti i piani del fascio aventi per asse la linea della dislocazione (e quindi il vettore di Burger) sono piani di scorrimento su cui la dislocazione può muoversi. Da ciò deriva la maggior mobilità di queste dislocazioni rispetto a quelle a spigolo. La dislocazione è detta a vite destrogira se il vettore di Burger ha verso discorde da quello della linea di dislocazione, a vite levogira se il vettore ha verso concorde.
- Le dislocazioni in un cristallo hanno frequentemente carattere misto, parzialmente a spigolo e parzialmente a vite, e formano quelle che vengono definite dislocazioni curvilinee (vedi figura sotto).
I cristalli reali contengono sempre una quantità piuttosto rilevante di dislocazioni, che, come detto, si possono spostare su piani di scorrimento ben definiti di una quantità pari al vettore di Burger; ciò comporta spostamenti di pochi, singoli atomi che sono solo una frazione dello stesso vettore di Burger. Il movimento della dislocazione termina poi sulla superficie libera, generando un gradino che è equivalente a quello che si otterrebbe spostando tutti gli atomi al di sopra del piano di scorrimento rispetto a quelli al di sotto, ma con una forza molto minore, e ciò spiega perché la deformazione plastica sia possibile applicando tensioni di taglio che sono una frazione minima rispetto a quelle teoriche necessarie a deformare un cristallo perfetto esente da dislocazioni.
Il processo di climb avviene in tappe successive in ogni punto nello stesso istante. Ne risulta che una dislocazione può suddividersi in piani paralleli vicini formando dei piccoli gradini detti “jog”. Sono invece detti “Kinks” i gradini di dislocazione che si muovono sullo stesso piano di scorrimento. Entrambi sono piccoli segmenti di una dislocazione che hanno lo stesso vettore di burger della linea di giacitura. I kink che hanno lo stesso piano di scorrimento della linea della dislocazione non impediscono il glide. Il movimento di un jog in una dislocazione a spigolo reca con sé la formazione di un ingente numero di vacanze, fondamentali nei meccanismi di deformazione ad elevate temperature.
Il processo di glide è favorito rispetto al climb per basse temperature, poiché richiede un’energia minore.
(Le dislocazioni vengono comunemente trattate utilizzando il vettore di Burger 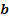 , identificato con questa procedura:
, identificato con questa procedura:
1. si definisce in maniera arbitraria una direzione positiva lungo la linea della dislocazione;
2. si costruisce un piano perpendicolare alla linea della dislocazione;
3. si traccia sul piano un circuito attorno alla dislocazione, movendosi di n vettori reticolari in ciascuna delle quattro direzioni mutuamente ortogonali; il circuito, orientato in senso orario guardando verso il senso positivo della linea, viene detto circuito di Burger;
4. il vettore necessario a chiudere il percorso è il vettore di Burger, ed è uguale al vettore di scorrimento.)
- Descrivere i difetti di punto.
Si hanno difetti di punto quando l’ordine di impacchettamento degli atomi in strutture geometriche ideali è variato puntualmente. Se ne distinguono diverse tipologie:
- Vacanze: siti reticolari in cui sono assenti degli atomi.
Questi difetti si formano già in fase di solidificazione, a seguito di imperfezioni di impacchettamento durante la cristallizzazione, ma sono anche il risultato delle vibrazioni atomiche, per cui aumentano di numero al crescere della temperatura (se aumenta l’energia termica aumenta la probabilità che un atomo migri dalla sua posizione reticolare).
Vacanze possono essere altresì prodotte da deformazioni plastiche, da tempre o da radiazioni (raggi γ).
La concentrazione di vacanze in materiali puri è minima per basse temperature, stimata pari ad una vacanza ogni 108 atomi. Per temperature prossime a quella di fusione la concentrazione aumenta ad 1 vacanza ogni 10³ atomi.
Il numero di vacanze in equilibrio (NV), per un data quantità di materiale, aumenta al crescere della temperatura in base alla relazione: 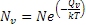 , in cui N è il numero di siti atomici totali, T la temperatura assoluta, k la costante di Boltzmann; QV è l’energia di attivazione (sostanzialmente l’energia vibrazionale richiesta per formare una vacanza).
, in cui N è il numero di siti atomici totali, T la temperatura assoluta, k la costante di Boltzmann; QV è l’energia di attivazione (sostanzialmente l’energia vibrazionale richiesta per formare una vacanza).
L’importanza di questo tipo di difetti è notevole, specialmente per quanto attiene alla deformazione ad elevata temperatura, resa possibile proprio dalla diffusione delle vacanze all’interno del reticolo.
Nel corso del raffreddamento le vacanze diffondono verso i bordi di grano, causando la scomparsa delle dislocazioni.
- Atomi auto-interstiziali: è possibile che in alcuni casi uno degli atomi nei siti reticolari si sposti in uno degli interstizi, dando origine ad una vacanza. Dal momento che in generale la dimensione degli atomi metallici è molto più elevata di quella degli interstizi, questo tipo di difetto causa severe distorsioni del reticolo, per cui è relativamente raro.
- Impurezze: atomi di elementi estranei in un metallo, la cui presenza porta alla costituzione di una soluzione solida, in cui gli atomi di soluto si trovano dispersi più o meno uniformemente. Possono essere di due tipi:
- le impurezze di tipo interstiziale sono atomi che vanno a disporsi negli interstizi fra i siti reticolari occupati, e per questo motivo sono generalmente piuttosto piccoli (ad esempio C e N), ma comunque più grandi degli interstizi, per cui la quantità di soluto che può essere ospitata in soluzione è relativamente piccola (meno del 10%).
- le impurezze di tipo sostituzionale sono atomi di soluto che vanno a sostituire atomi del solvente nei siti reticolari del cristallo; questo processo è regolato dalle leggi di Hume-Rothery, le cui condizioni sono: differenza fra i raggi atomici < 15%, stessa struttura cristallina, stessa valenza e elettronegatività analoga. Questi fattori incidono sulla quantità massima di solvente in soluzione, superata la quale si ha la formazione di una nuova fase.
- Nei cristalli ionici i difetti di punto sono più complessi, per la necessità di mantenere la neutralità elettrica:
- Difetto di Schottky: bivacanza catione-anione che si genera quando due ioni di carica opposta si allontanano da un cristallo ionico.
- Difetto di Frenkel: doppio difetto vacanza-autointerstiziale che si origina se uno ione si muove in un sito interstiziale, dando origine quindi anche ad una vacanza nel suo sito originario.
La presenza di questi difetti nei cristalli ionici aumenta la loro conduttività elettrica.
- Composti interstiziali: Si possono ottenere quando atomi di un elemento (con caratteristiche metalloidiche) si sistemano ordinatamente negli interstizi di un reticolo metallico base. La loro formazione è possibile per l'affinità fra atomi di polarità opposte. Si hanno composti interstiziali con atomi di metalloidi, le dimensioni dei quali sono molto piccole, per esempio: C, N, B. In questi composti gli atomi di metallo, ovviamente vengono a trovarsi in soprannumero rispetto agli atomi di metalloide.
(Gli spazi interstiziali, spazi vuoti che si formano fra gli atomi del reticolo cristallino, possono essere di due tipi:
- tetraedrici, vuoti formati dall'addensamento di tre sfere su uno stesso piano ed una quarta su un piano differente: si forma un tetraedro con un vuoto al centro in grado di ospitare un atomo di piccolo diametro;
- ottaedrici, si ottengono sovrapponendo due terne triangolari di sfere sfalsate tra loro di 60°: si forma una lacuna a forma di ottaedro con dimensioni maggiori di quella tetraedrica.
[CCC: 4 siti tetraedrici per ognuna delle 6 facce; CFC, HCP: attorno ad ogni atomo 3 lacune tetraedriche, ciascuna alternata ad una ottaedrica.])
- Descrivere i difetti di superficie.
I difetti planari riscontrabili in un metallo sono rappresentati da:
- Bordi di grano, considerati una zona difettiva in quanto, essendo meno densi, sono in grado di favorire i processi di diffusione. A seconda del grado di disorientazione fra un cristallo e quello vicino, si parla di:
- Confini a basso angolo; possono essere schematizzati come un allineamento di dislocazioni a spigolo dello stesso segno. Confini a basso angolo delimitano i sottograni, unità, il cui interno è relativamente libero da dislocazioni, che si formano all’interno di grani deformati ad elevata temperatura. Si tratta di uno dei meccanismi tipici del ripristino, cioè della riduzione della densità di dislocazioni, che, ad alta temperatura, si riarrangiano a formare strutture a più bassa energia quali sono i confini di sottograno. A temperatura ambiente, la mobilità delle dislocazioni è molto più ridotta, e quindi le dislocazioni non riescono a formare sottograni, ma al massimo formano delle celle (porzioni di cristallo suddivise da pareti, anch’esse formate da grovigli di dislocazioni, meno organizzate rispetto ai confini di sottograno).
- Confini ad alto angolo; sono i confini di grano veri e propri; sostanzialmente la disorientazione fra i cristalli adiacenti aumenta man mano che altre dislocazioni si vengono ad aggiungere al confine. Il confine di grano rappresenta in generale una zona più reattiva rispetto al resto del cristallo; inoltre, atomi di impurezze tendono a segregare su di esso. Nello stesso modo il bordo di grano è sede preferenziale per la formazione di nuove fasi (precipitazione).
- Geminati (twins): si tratta di un caso speciale di confini di grano, rispetto al quale esiste una simmetria speculare fra le porzioni di reticolo. La regione fra una coppia di confini di questo tipo si definisce twin (geminato), e la sua formazione è dovuta ad uno scorrimento di atomi rispetto alla loro posizione di equilibrio; tale spostamento può avvenire sia durante la deformazione plastica che durante il trattamento termico di determinati materiali (annealing twins). Mentre i geminati da trattamento termico sono tipici dei cristalli cfc, i geminati da deformazione si trovano soprattutto nei cristalli ccc e hcp. La geminazione è un modo di deformazione plastica che corrisponde al livello del cristallo ad una traslazione dei piani parallelamente gli uni sugli altri di una quantità proporzionale alla distanza d dal piano di geminazione, in modo tale il cristallo deformato diviene simmetrico del cristallo non deformato rispetto al piano di geminazione, ed è definita da un piano, una direzione ed un tasso di geminazione. Come nel caso dello scorrimento, esistono dei sistemi di geminazione in funzione della struttura cristallografica e si definisce una sollecitazione critica τ(c) di geminazione, che varia egualmente con la struttura cristallografica e la temperatura. Nel caso del sistema:
- CCC, la geminazione è il modo principale di deformazione a bassa temperatura;
- CFC, τ(c) di geminazione resta sempre superiore al τ(c) di scorrimento: non vi è geminazione per deformazione plastica;
- EC, il tasso di geminazione è molto debole: la geminazione è il modo principale di deformazione per i metalli esagonali.
Dal punto di vista della microscopia ottica, la geminazione si differenzia dallo scorrimento perché può essere osservato dopo pulitura ed attacco (la parte geminata ha una orientazione differente della parte non geminata).
- Difetti di impilamento (stacking fault): consistono in un’interruzione della sequenza regolare del reticolo cristallino in una regione localizzata del cristallo. Ad esempio, nei cristalli cfc l’impilaggio dei piani ad elevato fattore di impacchettamento è del tipo ABCABCABC, ma in caso di stacking fault la sequenza diventa ABCBCABC (si forma cioè uno strato con impilaggio tipico della struttura hcp). Questo tipo di difetto è naturalmente associato ad un aumento dell’energia immagazzinata dal cristallo (mentre la tendenza naturale sarebbe quella di minimizzarla):
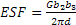 . Tanto minore è l’energia del difetto tanto più difficile risulta la ricombinazione delle dislocazioni estese e quindi il fenomeno dello scorrimento incrociato. Materiali con alta energia del difetto d’impilaggio incrudiscono, quindi, più velocemente.
. Tanto minore è l’energia del difetto tanto più difficile risulta la ricombinazione delle dislocazioni estese e quindi il fenomeno dello scorrimento incrociato. Materiali con alta energia del difetto d’impilaggio incrudiscono, quindi, più velocemente. - Anche la ripetizione di alcuni difetti di punto, come cluster di interstiziali o di vacanze, è considerata difetto di superficie, assieme ai cosiddetti difetti di orientazione (disclinazioni), caratterizzate da un angolo di tilt tra due zone adiacenti del cristallo.
- Descrivere i difetti di volume.
A seconda dei materiali di base e della loro struttura possono essere definite diverse tipologie di difetti di volume:
- Vuoti o porosità (cluster di vacanze): causate dall’evoluzione gassosa durante il raffreddamento di un metallo (porosità da gas) e dal ritiro in volume (porosità di ritiro) tipico di molti metalli. Se le porosità sono arrotondate e le superfici interne dei pori non si sono ossidate, è probabile che durante una laminazione vengano in gran parte riassorbite. In particolare, la porosità da idrogeno è di due tipi:
- Primaria o inter-dendritica e molto dannosa, che si verifica quando il contenuto di idrogeno è elevato e determina la formazione di bolle durante la ricottura e di lacerazioni durante le lavorazioni a caldo; un suo eccesso determina una riduzione della sezione resistente e quindi riduce le proprietà meccaniche.
- Secondaria o sub-critica, che consiste di pori di piccole dimensioni uniformemente distribuiti, che possono allargarsi durante la ricottura.
- Inclusioni (cluster di impurezze).
- Descrivere il fenomeno di rafforzamento per invecchiamento o precipitazione.
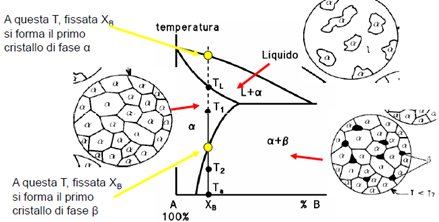 Per invecchiamento in generale si intende quel trattamento termico volto alla precipitazione di particelle fini che possono garantire, in certe famiglie di leghe, un consistente innalzamento della resistenza meccanica. Consideriamo una lega di composizione XB, a temperatura ambiente in condizioni di equilibrio (quelle corrispondenti al diagramma di stato): questa sarà costituita da una soluzione solida α e da una frazione modesta di fase β; tale fase secondaria, formatasi in seguito della diminuzione di solubilità di B nella soluzione solida, in condizioni di equilibrio avrà la morfologia di precipitati grossolani, molto distanti gli uni dagli altri, spesso localizzati sul confine di grano. Il contributo di rafforzamento dovuto a questi precipitati è, sostanzialmente, trascurabile. Si supponga ora di riscaldare la lega fino alla temperatura T1, e di mantenerla a tale temperatura un tempo sufficiente ad avere la completa omogeneità delle distribuzioni di temperatura all’interno del pezzo (solubilizzazione). A questa temperatura, la lega sarà costituita da una soluzione solida di B in A. Se si opera una tempra fino a temperatura ambiente Ta (un raffreddamento sufficientemente veloce, per esempio tramite immersione in acqua), i meccanismi diffusionali non avranno il tempo di avvenire, tanto che la lega si manterrà monofasica. È chiaro che questa condizione è ben lontana da quella di equilibrio leggibile sul diagramma di stato; in effetti, la soluzione solida che si ottiene dopo tempra viene definita sovrassatura ed è metastabile. In sostanza tale soluzione tende a depositare, più o meno velocemente a seconda della natura della lega, particelle di fase β anche a temperatura ambiente, in modo da potersi avvicinare il più possibile alle condizioni di equilibrio e da minimizzare l’energia interna immagazzinata durante il trattamento di tempra. Nella maggior parte dei casi, questa precipitazione di fase β che avviene a temperatura ambiente è estremamente lenta, e viene definita invecchiamento naturale.
Per invecchiamento in generale si intende quel trattamento termico volto alla precipitazione di particelle fini che possono garantire, in certe famiglie di leghe, un consistente innalzamento della resistenza meccanica. Consideriamo una lega di composizione XB, a temperatura ambiente in condizioni di equilibrio (quelle corrispondenti al diagramma di stato): questa sarà costituita da una soluzione solida α e da una frazione modesta di fase β; tale fase secondaria, formatasi in seguito della diminuzione di solubilità di B nella soluzione solida, in condizioni di equilibrio avrà la morfologia di precipitati grossolani, molto distanti gli uni dagli altri, spesso localizzati sul confine di grano. Il contributo di rafforzamento dovuto a questi precipitati è, sostanzialmente, trascurabile. Si supponga ora di riscaldare la lega fino alla temperatura T1, e di mantenerla a tale temperatura un tempo sufficiente ad avere la completa omogeneità delle distribuzioni di temperatura all’interno del pezzo (solubilizzazione). A questa temperatura, la lega sarà costituita da una soluzione solida di B in A. Se si opera una tempra fino a temperatura ambiente Ta (un raffreddamento sufficientemente veloce, per esempio tramite immersione in acqua), i meccanismi diffusionali non avranno il tempo di avvenire, tanto che la lega si manterrà monofasica. È chiaro che questa condizione è ben lontana da quella di equilibrio leggibile sul diagramma di stato; in effetti, la soluzione solida che si ottiene dopo tempra viene definita sovrassatura ed è metastabile. In sostanza tale soluzione tende a depositare, più o meno velocemente a seconda della natura della lega, particelle di fase β anche a temperatura ambiente, in modo da potersi avvicinare il più possibile alle condizioni di equilibrio e da minimizzare l’energia interna immagazzinata durante il trattamento di tempra. Nella maggior parte dei casi, questa precipitazione di fase β che avviene a temperatura ambiente è estremamente lenta, e viene definita invecchiamento naturale.
Si supponga ora di riscaldare la soluzione solida sovrassatura alla temperatura T2 (invecchiamento artificiale): i meccanismi diffusionali, faranno sì che la precipitazione di fase β sia notevolmente accelerata; a questa temperatura si avrà dapprima la formazione di molti nuclei composti da pochi atomi, che cresceranno fino a diventare particelle fini, molto numerose e distribuite nella matrice. La distribuzione ha spesso caratteristiche di eterogeneità perché la nucleazione delle particelle avviene preferenzialmente su difetti (dislocazioni, bordi di sottograno o di grano).
In maniera sintetica si può dire che il processo di precipitazione avviene seguendo le diverse fasi:
- si formano clusters (grappoli) di atomi; si nucleano poi le prime particelle;
- i nuclei cominciano a crescere, mentre contemporaneamente si formano altri piccoli nuclei;
- una volta raggiunta la frazione in volume di seconda fase prevista dal diagramma di stato all’equilibrio a quella temperatura, le particelle cominciano a crescere in maniera competitiva; in altre parole le particelle più grandi tendono a crescere a spese di quelle più piccole, che si dissolvono; il processo è guidato dalla necessità di ridurre l’energia di interfaccia fra particelle e matrice, cioè di ottenere la configurazione di minima entalpia di processo; pochi grossi precipitati comportano un’energia di interfaccia molto minore rispetto a moltissimi precipitati fini.
Utilizzando tempi di invecchiamento sufficientemente lunghi, si avrebbe una microstruttura relativamente simile a quella ottenibile tramite raffreddamenti quasi-statici. Esiste una dimensione ottimale dei precipitati, in generale piuttosto fine, che garantisce al materiale la migliore resistenza meccanica. Bisogna fare in modo quindi che la precipitazione sia completata, evitando però che abbia inizio l’accrescimento competitivo delle particelle, che darebbe una resistenza insufficiente. Il fenomeno di addolcimento legato all’accrescimento competitivo viene definito sovrainvecchiamento, ed è naturalmente condizione da evitare, a meno che non si voglia ottimizzare la duttilità della lega, come si fa, ad esempio, prima di sottoporre il materiale a lavorazioni meccaniche di deformazione plastica.
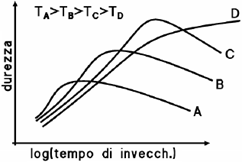 Oltre al tempo, anche la temperatura di invecchiamento gioca un ruolo fondamentale: si nota che al suo innalzamento, il picco della curva di durezza, corrispondente alla condizione di massima resistenza della lega, si sposta verso tempi di trattamento più brevi, ed è comunque sempre più basso che non alle temperature inferiori. Temperature troppo basse, d’altra parte, richiederebbero tempi di trattamento troppo lunghi per dare effetti apprezzabili; esiste quindi un optimum (combinazione di temperatura e tempo di trattamento ottimale, che consente di massimizzare le caratteristiche resistenziali della lega) che costituisce un compromesso tra tempi di invecchiamento ragionevolmente brevi e valori di picco della durezza elevati.
Oltre al tempo, anche la temperatura di invecchiamento gioca un ruolo fondamentale: si nota che al suo innalzamento, il picco della curva di durezza, corrispondente alla condizione di massima resistenza della lega, si sposta verso tempi di trattamento più brevi, ed è comunque sempre più basso che non alle temperature inferiori. Temperature troppo basse, d’altra parte, richiederebbero tempi di trattamento troppo lunghi per dare effetti apprezzabili; esiste quindi un optimum (combinazione di temperatura e tempo di trattamento ottimale, che consente di massimizzare le caratteristiche resistenziali della lega) che costituisce un compromesso tra tempi di invecchiamento ragionevolmente brevi e valori di picco della durezza elevati.
- Descrivere il fenomeno di rafforzamento per invecchiamento o precipitazione.
Il meccanismo di indurimento per precipitazione consiste in un aumento della difficoltà nel moto delle dislocazioni a seguito di un’opportuna distribuzione di particelle all’interno dei grani.
È opportuno sia evitare la formazione dei precipitati a bordo grano, dal momento che questo si comporta già come una barriera al moto dislocazionale, sia ottenere una distribuzione di particelle quanto più omogenea possibile, poiché una diversità di concentrazione nei precipitati comporta anche una diversità nelle proprietà meccaniche locali. Anche la dimensione delle particelle assume una notevole rilevanza: a dimensioni più piccole corrispondono proprietà meccaniche migliori.
Una differenza fondamentale (soprattutto per leghe di Al) è quella tra:
- precipitati coerenti (composti intermetallici), caratterizzati da stechiometria diversa da quella della matrice ma struttura uguale: l’effetto di indurimento consiste principalmente nel fatto che la dislocazione non è più libera di muoversi nel reticolo perché questo è distorto e quindi si ferma.
- precipitati incoerenti, che viceversa presentano stechiometria uguale a quella della matrice ma struttura differente: l’effetto di indurimento è dovuto sia ad un aumento della difficoltà nel moto della dislocazione che ad un incremento nella concentrazione delle dislocazioni tramite la nascita di loop attraverso il meccanismo di Orowan.
L’indurimento per precipitazione viene ottenuto attraverso un trattamento termico che consiste di più stadi:
- Solubilizzazione, condotta ad una temperatura superiore a quella corrispondente al limite di solubilità della percentuale di soluto in esame all’interno del solvente per un tempo sufficiente a garantirne l’omogeneizzazione;
- Tempra, che consiste in un rapido raffreddamento del materiale a temperatura ambiente o dell’azoto liquido (tempra criogenica);
- Invecchiamento (aging), la parte fondamentale del trattamento che prevede il mantenimento della lega ad una temperatura intermedia tra quella di solubilizzazione e quella ambiente. Sia la temperatura di invecchiamento che la durata del trattamento influenzano pesantemente la microstruttura che si ottiene e di conseguenza le proprietà meccaniche della lega.
Temperatura di invecchiamento: dev’essere mantenuta minore della temperatura di solubilizzazione. Il processo è termicamente attivato e di conseguenza la velocità del processo di invecchiamento aumenta all’aumentare della temperatura; a temperature più alte servono tempi minori per avere un’analoga precipitazione. Con un’opportuna regolazione della temperatura di invecchiamento si può inoltre favorire la fase di nucleazione o la fase di crescita: in generale per sottoraffreddamenti elevati si ha una prevalenza del fenomeno di nucleazione e si ottiene una distribuzione di precipitati più piccoli e in numero maggiore, mentre a temperature più elevate si hanno dei precipitati più grossi.
Composizione chimica: ad un aumento di percentuale dell’elemento in lega corrisponde un aumento della temperatura di solubilizzazione. Inoltre, il tempo di solubilizzazione dell’elemento in lega aumenta, concorrendo a far aumentare i costi di produzione e ad aumentare la probabilità di ottenere una grana più grossa. Si può anche notare che la cinetica di nucleazione ha un massimo a temperatura minore rispetto alla cinetica di accrescimento e quindi, con un opportuna regolazione della temperatura di invecchiamento, si può favorire un fenomeno o l’altro. Si è quindi in grado di ottenere un materiale con molti precipitati piccoli agendo a temperature più basse, e viceversa. Si può addirittura suddividere il ciclo termico di invecchiamento in due fasi distinte, con definite temperature e tempi di lavoro, per ottimizzare al meglio le fasi di nucleazione ed accrescimento.
Composizione chimica: si è stabilito che ad un aumento di percentuale dell’elemento in lega aumenta la temperatura di solubilizzazione. Si nota inoltre che il tempo di solubilizzazione non diminuisce in quanto si deve solubilizzare una percentuale maggiore. Questi fatti concorrono a far aumentare i costi di produzione perché si deve lavorare a temperature maggiori per tempi analoghi ed inoltre, per questo motivo, si rischia di ottenere una grana più grossa. Tuttavia un aumento di percentuale dell’elemento in lega causa anche un aumento di percentuale di soluto dopo invecchiamento e un conseguente aumento della durezza massima. Una accurata analisi delle esigenze di durezza e dei fattori economici sta quindi alla base della scelta della lega. Si nota inoltre che una maggiore sovrasaturazione porta ad un conseguente aumento della "forza motrice" del processo di invecchiamento e di conseguenza della relativa cinetica. Ciò non è necessariamente positivo, in quanto molte leghe possono invecchiare spontaneamente a temperatura ambiente e aumentare questa cinetica al punto di portarla su scale temporali paragonabili alla vita del materiale, e ciò potrebbe causare overaging "spontaneo", portando al crollo delle proprietà meccaniche.
- Descrivere il fenomeno di rafforzamento per soluzione solida.
Il rafforzamento per soluzione solida consiste nell’aumento della resistenza di un metallo in seguito all’aggiunta di uno o più elementi di lega che formano una soluzione solida, ed è dovuto principalmente a due fattori:
- il fattore di grandezza relativa, ossia la differenza della grandezza di atomi del soluto e del solvente. Questa incide sul rafforzamento a causa delle deformazioni prodotte nel reticolo cristallino, le quali generano sollecitazioni di tipo tensionale di trazione e di compressione che interagiscono con le dislocazioni: gli atomi di soluto più grandi rispetto a quelli del reticolo del solvente si sistemano nella zona di tensione della dislocazione, mentre quelli più piccoli nella zona di compressione, abbassando comunque in entrambi i casi l’energia del sistema. A questo punto, il movimento delle dislocazioni risulta ostacolato, in quanto, per muoversi, queste devono trascinarsi dietro l’intera nuvola di atomi in soluzione, cosa che ovviamente comporta tensioni più elevate che non nel metallo puro;
- l’ordine a corto raggio delle soluzioni solide che vengono a formarsi, che raramente risultano miscele casuali, in quanto spesso hanno luogo dei fenomeni di raggruppamento di atomi simili, per cui il movimento delle dislocazioni risulta ostacolato a causa dell’esistenza di sub-strutture con differenti legami.
Da stime teoriche e sperimentali effettuate l’equazione che rende l’effetto rafforzativo dovuto ad atomi in soluzione solida è data da: 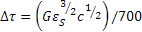 .
.
- Descrivere il fenomeno di rafforzamento per affinamento del grano.
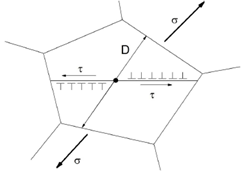 , in cui RS0.2 è la tensione di snervamento del materiale, σiè resistenza intrinseca del cristallo, ky è un parametro che misura l’effetto di rafforzamento dei confini di grano, e d è la dimensione media dei grani. Tuttavia, esistono anche altre teorie che nei bordi di grano vedono piuttosto una sorgente per la generazione di nuove dislocazioni. L’entità del rafforzamento dipende anche dalla struttura dei bordi di grano e dal grado di disorientazione tra i diversi grani.
, in cui RS0.2 è la tensione di snervamento del materiale, σiè resistenza intrinseca del cristallo, ky è un parametro che misura l’effetto di rafforzamento dei confini di grano, e d è la dimensione media dei grani. Tuttavia, esistono anche altre teorie che nei bordi di grano vedono piuttosto una sorgente per la generazione di nuove dislocazioni. L’entità del rafforzamento dipende anche dalla struttura dei bordi di grano e dal grado di disorientazione tra i diversi grani.
Il modello più accreditato, comunque, considera le sorgenti di dislocazioni all’interno dei singoli grani; tali dislocazioni incontrano resistenza da parte del reticolo τ0, che si oppone alla sollecitazione tangenziale τa generata dalla sollecitazione esterna σ. Quindi la sollecitazione tangenziale effettiva che produce scorrimento sarà: 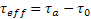 .
.
Questo metodo di rafforzamento è comunemente utilizzato per ottenere, tramite laminazioni controllate, lamiere di acciaio basso-alligato con elevata resistenza, risultando, soprattutto per i materiali a struttura ccc, un'ottima soluzione in grado di limitare il moto delle dislocazioni.
-  Descrivere brevemente i vari meccanismi di rafforzamento e il loro effetto.
Descrivere brevemente i vari meccanismi di rafforzamento e il loro effetto.
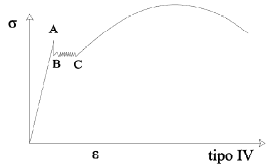
- Incrudimento (rafforzamento per deformazione) -
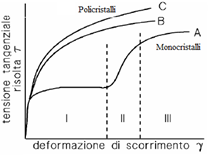
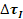 : meccanismo per il quale le dislocazioni, se presenti in numero troppo elevato nel materiale, tendono ad interagire fra loro e a bloccarsi vicendevolmente, aumentando la sua resistenza (vedi teoria della mesh – diagramma a lato).
: meccanismo per il quale le dislocazioni, se presenti in numero troppo elevato nel materiale, tendono ad interagire fra loro e a bloccarsi vicendevolmente, aumentando la sua resistenza (vedi teoria della mesh – diagramma a lato).
EFFETTI: diminuisce la tenacità del materiale, può essere eliminato elevando la temperatura, ha un’efficacia limitata nei materiali ad alta resistenza in cui il carico di snervamento è molto prossimo al carico ultimo in trazione.
- Rafforzamento per affinamento del grano o inoculazione -
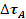 : si basa sul fatto che i bordi di grano, essendo delle regioni di disordine atomico, costituiscono degli ostacoli per le dislocazioni, che rimangono confinate all’interno dei grani; quindi, più piccoli sono i grani e più numerosi i bordi di grano, più difficile risulta il movimento delle dislocazioni e quindi la deformazione plastica del materiale.
: si basa sul fatto che i bordi di grano, essendo delle regioni di disordine atomico, costituiscono degli ostacoli per le dislocazioni, che rimangono confinate all’interno dei grani; quindi, più piccoli sono i grani e più numerosi i bordi di grano, più difficile risulta il movimento delle dislocazioni e quindi la deformazione plastica del materiale.
EFFETTI: fa aumentare sia resistenza (in modo limitato) che tenacità; l’affinamento del grano è deleterio per le applicazioni ad alta temperatura, il materiale diventa meno resistente al Creep; i bordi di grano sono percorsi preferenziali di diffusione e subiscono ingrossamento all’aumentare della temperatura.
- Rafforzamento per soluzione solida -
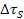 : è dovuto all’aggiunta di elementi di lega che formano soluzioni solide, per cui le dislocazioni hanno maggiore difficoltà a muoversi attraverso il reticolo del cristallo, essendo presenti atomi di soluto diversi, con differenti dimensioni o che si possono addensare in particolari zone.
: è dovuto all’aggiunta di elementi di lega che formano soluzioni solide, per cui le dislocazioni hanno maggiore difficoltà a muoversi attraverso il reticolo del cristallo, essendo presenti atomi di soluto diversi, con differenti dimensioni o che si possono addensare in particolari zone.
EFFETTI: l’aggiunta di atomi in soluzione solida produce un moderato aumento di resistenza; l’efficacia è limitata dalla solubilità dei diversi elementi; soluti con grande distorsione reticolare hanno bassa solubilità, mentre soluti interstiziali hanno un effetto molto limitato nei reticoli ccc. Possono però ridurre la suscettibilità alla corrosione e legarsi ad altri elementi per formare precipitati.
- Rafforzamento per invecchiamento o precipitazione (di particelle coerenti/semicoerenti, forme metastabili intermedie, o incoerenti, di equilibrio) -
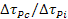 : consiste in un aumento della difficoltà nel moto delle dislocazioni a seguito di un’opportuna distribuzione di particelle all’interno dei grani, che avviene mediante solubilizzazione a temperatura superiore a quella del limite di solubilità, successiva tempra a temperatura ambiente e infine precipitazione spontanea del soluto (invecchiamento naturale) o indotta da un nuovo aumento di temperatura, minore però di quella di solubilizzazione (invecchiamento artificiale).
: consiste in un aumento della difficoltà nel moto delle dislocazioni a seguito di un’opportuna distribuzione di particelle all’interno dei grani, che avviene mediante solubilizzazione a temperatura superiore a quella del limite di solubilità, successiva tempra a temperatura ambiente e infine precipitazione spontanea del soluto (invecchiamento naturale) o indotta da un nuovo aumento di temperatura, minore però di quella di solubilizzazione (invecchiamento artificiale).
EFFETTI: è opportuno sia evitare la formazione dei precipitati a bordo grano (che già funziona da barriera al moto dislocazionale), sia ottenere una distribuzione di particelle quanto più omogenea possibile, poiché una diversità di concentrazione nei precipitati comporta anche una diversità nelle proprietà meccaniche locali. Inoltre, a dimensioni delle particelle più piccole corrispondono proprietà meccaniche della lega migliori.
- Rafforzamento per dispersione (di particelle incoerenti o coerenti/semicoerenti) -
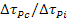 (leghe di Ni) in leghe fuse o whiskers).
(leghe di Ni) in leghe fuse o whiskers).
EFFETTI: necessita di dispersione di particelle molto fini per avere una grande efficacia di rafforzamento: particelle fini ma poco resistenti hanno un effetto molto moderato, perché facilmente by-passabili dalle dislocazioni. Nonostante ciò, ad alte temperature sono convenienti rispetto ai precipitati, che tenderebbero a diventare grossolani o a dissolversi. In genere conviene comunque utilizzare particelle il più fini possibile e il più dure possibile.
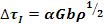
con: α=0.2 per CFC e α=0.4 per CCC, G=modulo elastico a taglio, b=vettore di Burger, ρ=densità delle dislocazioni, d=dimensione media dei grani, ky=parametro per l’effetto di rinforzamento dei confini di grano, ε e c=parametri empirici dipendenti da dimensione e concentrazione degli atomi di soluto, r e L=raggio e spaziatura delle particelle.
Le formule in grassetto hanno effetto di rafforzamento elevato, le altre effetto moderato.
 - Descrivere il rapporto tra dislocazioni e snervamento.
- Descrivere il rapporto tra dislocazioni e snervamento.
Molti metalli e leghe, come ad esempio gli acciai a basso tenore di carbonio, presentano nelle curve carichi-allungamenti, un tratto singolare al termine dello stadio di deformazione elastica. Dal suo esame si può rilevare come, al crescere della deformazione, dapprima il carico cresca con continuità, poi decresca bruscamente, poi fluttui attorno a un valore costante e infine cresca nuovamente. Si individuano sulla figura il limite di snervamento superiore, quello inferiore e l’allungamento che si ha per quest’ultimo carico definito come allungamento da snervamento.
Durante la sollecitazione l’insorgere dello snervamento non coinvolge tutto il provino, ma compare in certe zone dette bande di deformazione o bande di Lüders la cui formazione ha inizio nelle zone più sollecitate dei provini (ad esempio i raccordi di provini piatti per prove di trazione) allorché si raggiunge il limite di snervamento superiore.
Subito dopo la formazione delle bande iniziali, il carico scende al valore dello snervamento inferiore.
I bordi mobili delle bande si propagano poi lungo il provino provocando l’allungamento da snervamento; il limite inferiore di snervamento può essere inteso come il carico necessario alla propagazione delle bande di Lüders.
Durante l’allungamento da snervamento l’andamento della curva carichi-allungamenti è irregolare per la presenza di numerose oscillazioni ciascuna delle quali corrisponde alla formazione di una nuova banda di Lüders. Quando l’intero provino risulta coperto da bande di Lüders termina l’allungamento da snervamento e la curva riprende a salire.
Sperimentalmente si è anche osservato che lo snervamento può essere legato alla presenza di impurezze formate da atomi interstiziali o sostituzionali. Così la rimozione totale di C e N da un acciaio fa sparire il fenomeno dello snervamento e la curva carichi-allungamenti assume l’aspetto classico.
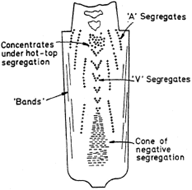
- Descrivere la struttura di un lingotto.
In un lingotto di distinguono generalmente tre zone:
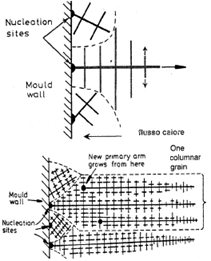 chill zone: caratterizzata da una crescita equiassica di cristalli sulle pareti del crogiolo; la sua formazione è dovuta al rapido raffreddamento del liquido al di sotto della temperatura di liquidus, che porta alla creazione di diversi nuclei solidi; se la temperatura di colata è bassa tutto il liquido si raffredderà velocemente e i cristalli precipitati nel fuso continueranno a crescere (nucleazione a big-bang), mentre se la temperatura è alta il liquido al centro del crogiolo rimarrà al di sopra del liquidus per lungo tempo, mentre la maggior parte dei cristalli rifonderà subito se si stacca dalle pareti del crogiolo.
chill zone: caratterizzata da una crescita equiassica di cristalli sulle pareti del crogiolo; la sua formazione è dovuta al rapido raffreddamento del liquido al di sotto della temperatura di liquidus, che porta alla creazione di diversi nuclei solidi; se la temperatura di colata è bassa tutto il liquido si raffredderà velocemente e i cristalli precipitati nel fuso continueranno a crescere (nucleazione a big-bang), mentre se la temperatura è alta il liquido al centro del crogiolo rimarrà al di sopra del liquidus per lungo tempo, mentre la maggior parte dei cristalli rifonderà subito se si stacca dalle pareti del crogiolo.- zona colonnare: caratterizzata da una crescita dendritica dei cristalli della zona equiassica, a causa di una diminuzione del gradiente di temperatura sulle pareti del crogiolo, che i cristalli tendono a seguire, crescendo principalmente nelle direzioni parallele al flusso di calore (cioè perpendicolarmente alle pareti).
- zona equiassica: consiste di grani equiassici orientati a caso al centro del lingotto, originati dalla rifusione delle braccia dendritiche e dal distacco delle braccia secondarie a causa dei moti convettivi generati dalle differenze di temperatura nel liquido, che vengono trasportate in altre zone, andando a rappresentare dei semi per la crescita nei nuovi grani. Una convezione debole crea pochi semi, per cui i cristalli finali saranno larghi.
- Descrivere gli ossidi.
L’equazione che porta alla formazione di idrogeno atomico (nell’Al), porta anche alla formazione di ossido. L’ossido di alluminio si riunisce in layers alla superficie del fuso, ma può essere inglobato nel metallo fuso in seguito a rifusione o semplicemente in seguito a movimentazione o flusso del fuso. In questo caso l’ossido è presente come inclusione; strati di ossido superficiale si formano anche direttamente in superficie per reazione dell’alluminio con l’ossigeno dell’ambiente. L’ossido che deve essere eliminato non è quello dello strato superficiale, che anzi svolge funzione protettiva, ma quello presente come inclusione nel fuso, che riduce la sezione resistente del prodotto, determinando anche concentrazioni di tensioni per cui sia le proprietà a fatica che quelle a trazione risultano ridotte. Le inclusioni riducono anche la fluidità del metallo fuso. Altro tipo di inclusioni sono carburi e fluoruri. Le inclusioni di ossido non possono essere eliminate per gravità (meccanismo spesso utilizzato per quelle più dense) perché hanno densità pari a quella del fuso. Perciò in genere si ricorre alla filtrazione del fuso su piatti di materiale ceramico o su letti di granuli.
- Descrivere i fenomeni di segregazione.
Il termine “segregazione” indica la disomogenea distribuzione dei componenti di una lega metallica rispetto al diagramma di stato. E’ quindi il fenomeno chimico-fisico per cui in una soluzione solida che si forma durante il processo di solidificazione di una soluzione liquida AB, la componente liquida che solidifica con temperatura di fusione più alta (sia ad esempio A) solidifica con la struttura nativa senza accusare l'effetto dell'altro componente della soluzione (B). Mano a mano che procede la solidificazione il processo conseguente di segregazione fa si che il liquido che rimane si arricchisca del componente con più bassa temperatura di fusione (B), rifiutato nelle precedenti interfacce di solidificazione e in ultima battuta formerà un'altra struttura tutta sua caratteristica del materiale B.
La segregazione si manifesta sia a livello microscopico che macroscopico. Si distinguono quindi:
- macro-segregazione, causata da contrazione per effetti termici, differenza di densità nel liquido interdendritico o tra il solido ed il liquido, correnti di convezione causate da gradienti di densità indotti dalla temperatura nel liquido.
- micro-segregazione (coring), causata dalla solidificazione delle dendriti per un composto non eutettico, che porta alla solidificazione di eutettici vicino ai rami dendritici, o da un aumento della concentrazione di soluto nel liquido.
 Sperimentalmente si è trovato che la velocità di raffreddamento influenza la spaziatura delle dendriti, ma non altera il profilo di concentrazione di soluto a patto che la morfologia delle dendriti non si alteri e al diffusione nel solido sia trascurabile.
Sperimentalmente si è trovato che la velocità di raffreddamento influenza la spaziatura delle dendriti, ma non altera il profilo di concentrazione di soluto a patto che la morfologia delle dendriti non si alteri e al diffusione nel solido sia trascurabile.
Si distinguono anche diverse tipologie di segregazione all’interno del lingotto:
- shrinkage (ritiro);
- segregazione inversa: originata dalla contrazione, in quanto quando le dendriti si inspessiscono, il liquido ricco di soluto fluisce verso la parte esterna del crogiolo per compensare la contrazione di volume, aumentando in loco la concentrazione di soluto;
- segregazione negativa: disomogeneità dovuta al fatto che solitamente, essendo il solido più denso del liquido, il primo tende ad andare a fondo con una composizione di soluto inferiore a quella del bulk, per cui si notano effetti di gravità nella formazione dei cristalli equiassici.
( Il fenomeno della fragilità al rosso è un tipico esempio di problema causato dalle segregazioni minori: lo zolfo e il fosforo si concentrano ai giunti dei grani in quanto poco solubili allo stato solido e creano un eutettico bassofondente; se si riscalda la lega per un trattamento termico o una lavorazione plastica a caldo, i giunti sono i primi a fondere e il pezzo metallico si disgrega, diventando un rottame senza possibilità di rimedio. )
- Descrivere la deformazione di un monocristallo metallico (aggiungere deformazione plastica per twinning).
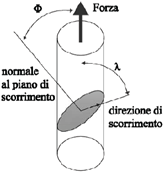 .
.
Se τR supera il valore critico τc si ha deformazione plastica, con scorrimento sul sistema di piani e direzioni considerato: si può dimostrare che il valore massimo della τR si ottiene per Ф=45°; questo spiega perché il campione tenda a deformarsi in questo modo:
Lo scorrimento di piani atomici l’uno sull’altro dovrebbe teoricamente avvenire quando: 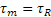 , ma misure sperimentali condotte hanno permesso di verificare che la sollecitazione necessaria a deformare un cristallo reale è enormemente inferiore a quella teorica, e ciò è dovuto alla presenza di difetti (soprattutto dislocazioni).
, ma misure sperimentali condotte hanno permesso di verificare che la sollecitazione necessaria a deformare un cristallo reale è enormemente inferiore a quella teorica, e ciò è dovuto alla presenza di difetti (soprattutto dislocazioni).
( (*)Alternativamente, essendo 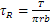 . )
. )
- Descrivere il fenomeno dell’hot cracking.
L’hot cracking è un fenomeno caratterizzato dalla creazione, all’interno del lingotto, di cricche spesso inter-granulari causate da stress interni sviluppati al raffreddamento, durante e dopo la solidificazione (le leghe di Al subiscono un ritiro volumetrico tra il 3,5% e l’8,5% durante la solidificazione). Per limitarne la presenza si può agire sulla forma del lingotto, evitando brusche variazioni di sezione o inadeguati angoli di raccordo, sulla dimensione dei grani, i quali, se fini, riducono la concentrazione di stress, o sugli alliganti, in quanto alcune leghe hanno bassa tendenza al cracking.
- Descrivere gli elementi che allargano e restringono il campo di esistenza del ferro γ.
Sulla verticale del ferro, oltre alla temperatura di fusione situata a 1538 °C, vi sono i punti A4 a 1394 °C ed A3 a 912 °C. Aggiungendo degli elementi al ferro questi possono:
- allargare il campo di esistenza del ferro γ (gammageni), provocando un innalzamento di A4 e un abbassamento di A3, in modo che al crescere della percentuale dell’elemento aggiunto cresce la distanza tra i due intervalli critici. Si distinguono inoltre due sottogruppi, a seconda del fatto che il campo:
- si allarghi illimitatamente (campo γ aperto), per cui l’innalzamento delle temperature dell’intervallo di trasformazione δ⇄γ giunge ad interferire con quelle di solidificazione dando origine ad una trasformazione peritettica: Ni, Mn, Co, Ru, Rh, Pd, Os, Ir, Pt. (Ricorda: NimMeno Rutelli Col Pd Rhiuscì ad Ostacolare l’Iraq. Peccato.)
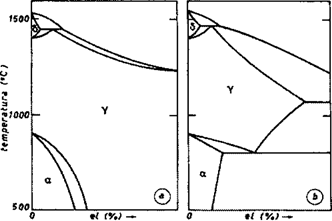 ): C, N, Cu, Zn, Au, con C ed N che formano soluzioni interstiziali. (Ricorda: il Cuoco Zante Augura Cani.)
): C, N, Cu, Zn, Au, con C ed N che formano soluzioni interstiziali. (Ricorda: il Cuoco Zante Augura Cani.)- restringere il campo di esistenza del ferro γ (alfageni), innalzando il punto A3 e abbassando il punto A4, in modo che al crescere della percentuale dell’elemento aggiunto diminuisce la distanza tra i due intervalli critici. Si distinguono di nuovo due sottogruppi, a seconda del fatto che il campo:
- confini con un altro campo di cristalli omogenei α (campo γ chiuso): Be, Al, Si, P, Ti, V, Cr, As, Mo, Sn, Sb, W (Ricorda: Bè, Allora Si Può Timbrare, Vero? Aspetti un Momento, Sono Subito Wafer.)
- confini con campi relativi ad altre fasi con equilibri eterogenei (campo γ ristretto): B, S, Zr, Nb, Ce, O, Ta (Ricorda: Oggi Cerco Tante Zebre BaSse Nel-bosco.)
Quando al ferro vengono aggiunti due elementi, possono accadere tre fenomeni fondamentali:
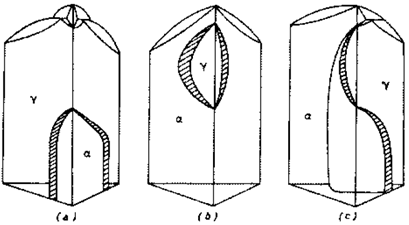 γ: il campo di esistenza della fase α è limitato attorno allo spigolo del ferro e solo per le basse temperature;
γ: il campo di esistenza della fase α è limitato attorno allo spigolo del ferro e solo per le basse temperature;- entrambi gli elementi restringono il campo γ, che rimane limitato ad una piccola zona adiacente allo spigolo del ferro tra le temperature A4 ed A3.
- Uno degli elementi produce un allargamento e l’altro un restringimento del campo γ: si ha una superficie ad andamento complesso che si appoggia alle linee dei diagrammi binari rappresentati sulle facce del prisma, e lo divide internamente nelle due regioni delle fasi α e γ.
- Descrivere il diagramma Fe-C.
 Nella forma in cui viene presentato solitamente, il diagramma ferro-carbonio presenta un composto intermetallico di formula Fe3C (carburo di ferro) chiamato cementite. La porzione del diagramma considerata è quella con un contenuto di C corrispondente alla composizione stechiometrica della cementite (6.69% in peso), per cui è più appropriato parlare di diagramma ferro-cementite. Difatti la porzione che interessa dal punto di vista tecnologico (acciaio e ghisa) coinvolge percentuali di C ben al di sotto di questo limite (in genere non si supera il 4%). Inoltre nel diagramma si assume per semplicità che la grafite sia completamente solubile nel Fe fuso, anche se di fatto tale solubilità è limitata al 5%. La cementite è in realtà un composto metastabile, mostrando la tendenza a decomporsi secondo la reazione: Fe3C → 3Fe + C per dare ferro e grafite. Il vero diagramma di equilibrio termodinamico è perciò il diagramma ferro-grafite. Tuttavia la reazione di decomposizione procede in maniera estremamente lenta e tale da non avere rilevanza pratica nelle normali condizioni ambientali. Seppure il diagramma ferro-grafite rappresenti quindi il diagramma stabile da un punto di vista termodinamico, la sua osservanza richiederebbe velocità di raffreddamento molto lente, lontane da quelle adottate nei comuni processi tecnologici. È per questo che si assume sempre come diagramma di riferimento il diagramma ferro-cementite (e a questo ci si riferisce quando si parla di diagramma ferro-carbonio). La presenza della grafite si rileva solo nelle leghe ad alto tenore di carbonio (2-4% ghise) grazie anche alla presenza di elementi promotori della sua formazione quali il silicio.
Nella forma in cui viene presentato solitamente, il diagramma ferro-carbonio presenta un composto intermetallico di formula Fe3C (carburo di ferro) chiamato cementite. La porzione del diagramma considerata è quella con un contenuto di C corrispondente alla composizione stechiometrica della cementite (6.69% in peso), per cui è più appropriato parlare di diagramma ferro-cementite. Difatti la porzione che interessa dal punto di vista tecnologico (acciaio e ghisa) coinvolge percentuali di C ben al di sotto di questo limite (in genere non si supera il 4%). Inoltre nel diagramma si assume per semplicità che la grafite sia completamente solubile nel Fe fuso, anche se di fatto tale solubilità è limitata al 5%. La cementite è in realtà un composto metastabile, mostrando la tendenza a decomporsi secondo la reazione: Fe3C → 3Fe + C per dare ferro e grafite. Il vero diagramma di equilibrio termodinamico è perciò il diagramma ferro-grafite. Tuttavia la reazione di decomposizione procede in maniera estremamente lenta e tale da non avere rilevanza pratica nelle normali condizioni ambientali. Seppure il diagramma ferro-grafite rappresenti quindi il diagramma stabile da un punto di vista termodinamico, la sua osservanza richiederebbe velocità di raffreddamento molto lente, lontane da quelle adottate nei comuni processi tecnologici. È per questo che si assume sempre come diagramma di riferimento il diagramma ferro-cementite (e a questo ci si riferisce quando si parla di diagramma ferro-carbonio). La presenza della grafite si rileva solo nelle leghe ad alto tenore di carbonio (2-4% ghise) grazie anche alla presenza di elementi promotori della sua formazione quali il silicio.
Forme allotropiche del ferro
Il ferro puro (che in natura non esiste), allo stato solido presenta tre (o quattro) forme allotropiche:
- ferro α: struttura CCC con a = 2.86 Å, stabile fino a 912 °C, magnetico fino a 768 °C (punto di Curie);
- ferro γ: struttura CFC con a = 3.63 Å, stabile tra 912 °C e 1394 °C;
- ferro δ: struttura CCC con a = 2.93 Å, stabile tra 1394 °C e 1538 °C (temperatura di fusione);
- (ferro β: struttura CCC con a = 2.86 Å, paramagnetico, dai 768 °C ai 912 °C - il ferro α andrebbe fino ai 768 °C)
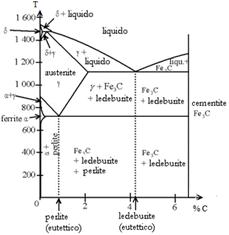
Punti critici sul diagramma:
A4 (1394 °C): temperatura di trasformazione ferro δ ⇄ ferro γ.
A3 (912 °C): temperatura di trasformazione ferro γ ⇄ ferro α (ipoeutettoidici).
A2 (768 °C): punto di Curie (non propriamente un punto critico).
A1 (723 °C): temperatura di trasformazione austenite eutettoidica ⇄ perlite.
Acm: Temperatura di trasformazione austenite ⇄ cementite (ipereutettoidici).
Fasi presenti nel diagramma:
fase liquida, fasi α, γ, δ del ferro, fase Fe3C (cementite).
Costituenti strutturali presenti nel diagramma:
- Ferrite α (ferrite): soluzione solida interstiziale con piccole quantità di C nel ferro α (CCC), che producono notevoli distorsioni, per cui la loro solubilità è molto limitata, con un valore massimo dello 0.02% (723° C).
- Austenite: soluzione solida interstiziale di C nel ferro γ (CFC), la cui struttura ne favorisce una maggiore solubilità (2% a 1134 °C); nel diagramma si ha un campo di stabilità dell'austenite più ampio di quello della ferrite.
- Ferrite δ: soluzione interstiziale del carbonio nel ferro δ (CCC). Valgono considerazioni analoghe a quelle fatte sulla ferrite, ma la maggiore costante di cella consente un lieve aumento della solubilità di C.
- Cementite (Fe3C): composto intermetallico (6,69% C) a reticolo rombico, forma piccoli cristalli irregolari.
- Perlite, eutettoide ferrite-cementite, costituito da grani (colonie), insiemi di lamelle alternate di ferrite e Fe3C.
- Ledeburite, eutettico austenite-cementite.
Differenza tra fasi e costituenti strutturali:
- una fase è un sistema chimico-fisico omogeneo, per cui formano una fase tutti quegli elementi cristallini aventi la stessa composizione chimica, lo stesso reticolo cristallino e quindi le stesse proprietà fisiche.
- un costituente strutturale è un sistema chimico-fisico che può essere omogeneo o eterogeneo, e quindi lo sono tutte le diverse specie di cristalli omogenei o grani eterogenei che possono essere messi in evidenza con opportuni attacchi metallografici, e che determinano con la loro forma, dimensione, distribuzione, quantità relativa e proprietà individuali le proprietà medie che caratterizzano la lega a livello macroscopico (ne derivano poi gli utilizzi).
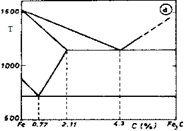 Per cui, quando i costituenti strutturali sono tutti rappresentati da cristalli omogenei, fasi e costituenti si identificano; se invece fanno parte della struttura grani eterogenei, questi rappresentano un costituente strutturale ma, essendo un miscuglio eterogeneo, in ciascun grano sono presenti due o più fasi.
Per cui, quando i costituenti strutturali sono tutti rappresentati da cristalli omogenei, fasi e costituenti si identificano; se invece fanno parte della struttura grani eterogenei, questi rappresentano un costituente strutturale ma, essendo un miscuglio eterogeneo, in ciascun grano sono presenti due o più fasi.
Trasformazioni invarianti:
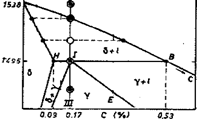 eutettica, a 1148 °C e 4,3% C:
eutettica, a 1148 °C e 4,3% C:
liquido ⇄ austenite (2,06%C) + Fe3C (6,67%C) = ledeburite.
- peritettica, a 1495 °C e 0,17% C:
liquido (0,53%C) + ferrite δ (0,09%C)⇄ austenite (0,17%C).
- eutettoidica, a 723 °C e 0,77% C:
austenite ⇄ ferrite α (0,02%C) + Fe3C (6,67%C) = perlite.
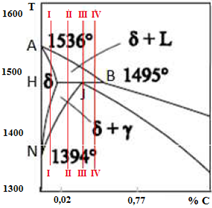 Solidificazione delle leghe fino a C = 0,53% (ACCIAI).
Solidificazione delle leghe fino a C = 0,53% (ACCIAI).
Lega I-I: all’incontro con la linea AB si separa il primo cristallo di soluzione solida δ; la solidificazione continua fino all’incontro della linea AH, dove rimane la sola fase δ, fino a che dalla linea NH cominciano a separarsi cristalli γ; alla linea NJ tutti i cristalli δ si saranno trasformati in cristalli γ.
Lega II-II: in HJB si ha la trasformazione peritettica tra cristalli δ con 0.09% C e il liquido con 0.53% C che porta alla formazione della nuova fase γ con 0.17% C e alla scomparsa della fase liquida; il sistema è costituito da cristalli δ e γ, e raffreddando avviene la stessa trasformazione del caso precedente, finché all’incontro con la linea N-J tutto la ferrite δ si è trasformato in austenite γ.
Leghe III-III (peritettica), IV-IV: tutti i cristalli δ scompaiono alla fine della trasformazione peritettica e l’unica fase solida presente è l’austenite γ.
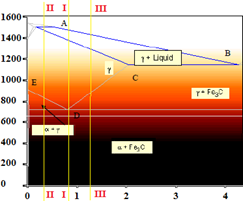
Solidificazione delle leghe da C = 0,53% a C = 2,11% (ACCIAI).
Lega I-I: C = 0.77 % (composizione eutettoide); si trova solo austenite che si raffredda fino al punto D, dove si trasforma in ferrite α e cementite.
Lega II-II: vi è sempre austenite fino all’incontro con la linea DE. In tal punto comincia la trasformazione del ferro γ in ferro α; la separazione della ferrite primaria continua a temperatura decrescente, mentre l’austenite continua ad arricchirsi in C seguendo la linea ED fino a che la trasformazione non raggiunge l’orizzontale. In tal punto si ha ferrite α ed austenite e la temperatura rimane costante finché tutta l’austenite si trasforma in perlite. Alla fine la lega risulta costituita da ferrite e perlite.
Lega III-III: vi è austenite fino all’incontro con la linea DC, dove appare la fase Fe3C (sistema monovariante). Al diminuire di T si ha l’incontro con la linea dell’eutettoide, dove coesistono ferro α, soluzione solida γ e Fe3C. Sotto tale temperatura vi è solo presenza di ferro α e Fe3C (sistema monovariante).
( C = 0,77%: acciaio eutettoidico (lega I); C < 0,77%: acciaio ipoeutettoidico (lega II); C > 0,77%: acciaio ipereutettoidico (lega III). )
Solidificazione delle leghe da C = 2,11% fino a C = 6,67% (GHISE).
 Lega I-I: la solidificazione comincia all’incontro con la linea AC con la deposizione del primo cristallo di austenite, che continua fino all’incontro con l’orizzontale ECF, dove si hanno austenite e liquido eutettico; a T costante avviene la solidificazione dell’eutettico e la lega risulta costituita da cristalli di austenite in matrice di ledeburite.
Lega I-I: la solidificazione comincia all’incontro con la linea AC con la deposizione del primo cristallo di austenite, che continua fino all’incontro con l’orizzontale ECF, dove si hanno austenite e liquido eutettico; a T costante avviene la solidificazione dell’eutettico e la lega risulta costituita da cristalli di austenite in matrice di ledeburite.
Lega II-II: C = 4.3% (composizione eutettico); la solidificazione comincia nel punto C, e procede a temperatura costante fino a completarsi, dando origine ad una struttura completamente ledeburitica.
Lega III-III: come per la lega I-I, ma con il segmento CD al posto di AC e cementite primaria al posto di austenite.
- Descrivere la struttura e la formazione della perlite.
La perlite è un aggregato di ferrite e cementite, costituito da grani (colonie) che sono insiemi di lamelle alternate di ferrite e cementite. La formazione della perlite avviene attraverso due stadi:
- nucleazione, che porta alla comparsa in seno all’austenite di piccolissimi nuclei di queste colonie che rappresentano l’inizio della trasformazione dell’austenite;
- accrescimento, che conduce all’ingrossamento dei nuclei precedentemente formatisi.
Per esaminare l’andamento nel tempo della trasformazione eutettoidica, la perlite va considerata in modo indipendente dalla sua costituzione bifasica, trattando quindi la colonia. Così facendo, questa può essere considerata di forma approssimativamente sferica, ed il modo più semplice per studiare l’andamento del fenomeno è di supporre che la velocità di nucleazione N e la velocità di accrescimento v siano costanti nel tempo, che la nucleazione sia casuale e infine che i nuclei, crescendo, finiscano con il toccarsi. Con queste ipotesi, detta f(t) la frazione di austenite trasformata al tempo t si ha: 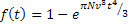 . È possibile dire che per intervalli di tempo inferiori al tempo di incubazione ti la frazione trasformata è pressoché nulla, mentre dopo il tempo tf di fine trasformazione, l’austenite è praticamente tutta trasformata. Dall’esame della legge è possibile capire che se le velocità N e v sono estremamente piccole, l’incremento della frazione trasformata nel tempo risulta molto basso.
. È possibile dire che per intervalli di tempo inferiori al tempo di incubazione ti la frazione trasformata è pressoché nulla, mentre dopo il tempo tf di fine trasformazione, l’austenite è praticamente tutta trasformata. Dall’esame della legge è possibile capire che se le velocità N e v sono estremamente piccole, l’incremento della frazione trasformata nel tempo risulta molto basso.
Qualora non si faccia avvenire la trasformazione eutettoidica in condizioni tali da avere tali velocità troppo piccole e inoltre non si favorisca la precipitazione preferenziale di una fase, si ha uno sviluppo normale dell’eutettoide. Se allora si ammette che i primi nuclei che si formano abbiano già struttura lamellare, si capisce che la crescita della colonia perlitica avviene sia per generazione alternata di lamelle di Fe3C e di ferro α (accrescimento laterale), sia per uno sviluppo delle lamelle parallelamente a se stesse (accrescimento frontale).
Se la prima lamella è ad esempio di Fe3C, la sua formazione comporta all’interfaccia carburo di ferro-ferro γ un notevole impoverimento di carbonio nel ferro γ, per cui si rende immediatamente possibile la formazione di una lamella di ferro α, con un processo ciclico, che si manifesta macroscopicamente sotto forma di colonia. Tutto questo avviene nel caso di trattamenti isotermici a temperature di pochi gradi sotto i punti critici o di raffreddamento lentissimo: aumentando infatti la velocità di raffreddamento, si verifica un abbassamento della temperatura di inizio della trasformazione. Se da una parte il coefficiente di diffusione del carbonio diminuisce al diminuire della temperatura, dall’altra fenomeni di sottoraffreddamento favoriscono la nucleazione. L’insieme di tutti questi fattori promuove una nuova accelerazione della trasformazione e la perlite diventa sempre più fine.
È comunque possibile, in seguito ad opportuni cicli termici, ottenere carburo di ferro invece che sotto forma di lamelle (perlite lamellare), in forma globulare (perlite globulare).
La spaziatura delle lamelle è un parametro notevolmente sensibile per l’effetto sulla resistenza. Considerando un volume di perlite di spessore d, e spaziatura delle lamelle S0; considerando la direzione di crescita indicata in figura il volume di austenite trasformata per spaziatura lamellare sarà S0δdxρ, dove ρ è la densità. L’energia libera disponibile per formare il volume di perlite sarà: 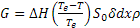 .
.
L’equazione precedente predice tre importanti aspetti della trasformazione:
- la spaziatura delle lamelle S0 diminuisce al diminuire della temperatura di trasformazione;
- la finezza delle lamelle è limitata dall’energia libera disponibile dalla trasformazione;
- vi è una relazione lineare tra la finezza delle lamelle e il sottoraffreddamento.
In definitiva all’aumentare del sottoraffreddamento aumenta la resistenza degli acciai perlitici. Inoltre la percentuale di perlite da il massimo contributo al rafforzamento negli acciai perlitici. Tutti gli elementi di lega tranne il Co fanno crescere la distanza intra-lamellare. Effetto della temperatura:
- al diminuire di T, la velocità di nucleazione N [nuclei/(mm3/s)] aumenta à noduli di perlite sempre più piccoli;
- al diminuire di T, diminuisce anche la distanza intra-lamellare à perliti sempre più fini.
Fonte: Giovanni Antonio Zappatore segnalazione via e-mail
Autore del testo: Giovanni Antonio Zappatore
Parola chiave google : Metallurgia riassunti tipo file : docx
Metallurgia riassunti parte 2
Visita la nostra pagina principale
Metallurgia riassunti
Termini d' uso e privacy