Sistema di misura internazionale

 

---

 

Sistema di misura internazionale

 

I riassunti, le citazioni e i testi contenuti in questa pagina sono utilizzati per sole finalità illustrative didattiche e scientifiche e vengono forniti gratuitamente agli utenti.

 

LE UNITÀ DI MISURA DEL SISTEMA INTERNAZIONALE (2007)

§A1.1 Le unità di misura fondamentali

Quantità fisica	Simbolo della quantità fisica	Nome dell'unità SI	Simbolo dell'unità SI
lunghezza	l	metro	m
massa	m	chilogrammo	kg
tempo	t	secondo	s
corrente elettrica	I, i	ampere	A
temperatura termodinamica	T	kelvin	K
quantità di sostanza	n	mole	mol
intensità luminosa	IV	candela	cd

 

- Il metro è definito come la distanza percorsa dalla luce nel vuoto in un intervallo di tempo pari a 1/299 792 458 di secondo (1983).

- Il chilogrammo è la massa di un particolare cilindro di altezza e diametro pari a 0,039 m di una lega di platino-iridio depositato presso l'Ufficio internazionale dei pesi e delle misure a Sèvres, in Francia. (1875)

- Il secondo è definito come la durata di 9 192 631 770 periodi della radiazione corrispondente alla transizione tra due livelli iperfini, da (F=4, MF=0) a (F=3, MF=0), dello stato fondamentale dell'atomo di cesio-133 (1967).

- L’ ampere è l'intensità di corrente elettrica che, se mantenuta in due conduttori lineari paralleli, di lunghezza infinita e sezione trasversale trascurabile, posti a un metro di distanza l'uno dall'altro nel vuoto, produce tra questi una forza pari a 2 • 10-7 newton per metro di lunghezza. (1946)

- Il kelvin è definito come 1/273,16 della temperatura termodinamica del punto triplo dell'acqua. (1862)

- La mole viene definita come la quantità di sostanza di un sistema che contiene un numero di entità elementari pari al numero di atomi presenti in 12 grammi di carbonio-12 (numero di Avogadro: 6,022 • 1023) . (1971)

- La candela è pari all'intensità luminosa, in una data direzione, di una sorgente emettente una radiazione monocromatica di frequenza pari a 540 • 1012 hertz e di intensità radiante in quella direzione di 1/683 di watt per steradiante (1982).

§A1.2 Le unità di misura derivate (di interesse elettrotecnico)

La maggior parte delle grandezze derivate provengono da una moltiplicazione o una divisione di grandezze di base. Alcune di esse hanno nomi particolari. In questo modo, non solo si vede immediatamente la relazione che intercorre tra due grandezze, ma, con un controllo dimensionale, lo studente ha una prima possibilità di verificare la possibile correttezza del proprio lavoro.

 

Quantità fisica	Simbolo	Nome dell'unità SI	Simbolo dell'unità SI
frequenza	f, ν	hertz	Hz	s−1
forza	F	newton	N	kg · m · s−2
pressione, sollecitazione	p	pascal	Pa	N · m−2
energia, lavoro	E	joule	J	N · m
potenza, flusso radiante	P, W	watt	W	J · s−1
carica elettrica	q	coulomb	C	A · s
tensione elettrica, potenziale	v	Volt	V	J · C−1
resistenza elettrica	R	Ohm	Ω	V · A−1
conduttanza elettrica	G	Siemens	S	A · V−1
capacità elettrica	C	Farad	F	C · V−1
induzione magnetica	B	Tesla	T	V · s · m−2
flusso magnetico	Φ(B)	weber	Wb	V · s
induttanza	L	henry	H	V · s · A−1
temperatura	T	kelvin	°C	K
angolo piano	φ, θ	radiante	rad	1
angolo solido	Ω	steradiante	sr	1
flusso luminoso		lumen	lm	cd · sr
illuminamento		lux	lx	cd · sr · m−2
rifrazione	D	diottria	D	m−1
attività di un radionuclide		becquerel	Bq	s−1
dose assorbita		gray	Gy	J · kg−1
dose equivalente		sievert	Sv	J · kg−1

 

A.1.3 Prefissi

Le unità SI possono avere prefissi per rendere più comodamente utilizzabili grandi e piccole misurazioni. Si noti l'importanza di utilizzare correttamente i simboli maiuscoli e minuscoli per evitare ambiguità..

 

	Prefisso	Simbolo	Nome	Equivalente decimale
1024	yotta	Y	Quadrilione	1 000 000 000 000 000 000 000 000
1021	zetta	Z	Triliardo	1 000 000 000 000 000 000 000
1018	exa	E	Trilione	1 000 000 000 000 000 000
1015	peta	P	Biliardo	1 000 000 000 000 000
1012	tera	T	Bilione	1 000 000 000 000
109	giga	G	Miliardo	1 000 000 000
106	mega	M	Milione	1 000 000
103	kilo o chilo	k	Mille	1 000
102	etto	h	Cento	100
10	deca	da	Dieci	10
10−1	deci	d	Decimo	0,1
10−2	centi	c	Centesimo	0,01
10−3	milli	m	Millesimo	0,001
10−6	micro	µ	Milionesimo	0,000 001
10−9	nano	n	Miliardesimo	0,000 000 001
10−12	pico	p	Bilionesimo	0,000 000 000 001
10−15	femto	f	Biliardesimo	0,000 000 000 000 001
10−18	atto	a	Trilionesimo	0,000 000 000 000 000 001
10−21	zepto	z	Triliardesimo	0,000 000 000 000 000 000 001
10−24	yocto	y	Quadrilionesimo	0,000 000 000 000 000 000 000 001

 

§A1.4 Unità di misura tollerate nel SI

Le seguenti unità di misura non fanno parte del Sistema Internazionale, ma il loro uso viene tollerato, anche in ambienti ufficiali.

 

Nome	Simbolo	Equivalenza in termini di unità fondamentali SI
minuto	min	1 min = 60 s
ora	h	1 h = 60 min = 3 600 s
giorno	d	1 d = 24 h = 86 400 s
grado	°	1° = (π/180) rad
minuto primo	′	1′ = (1/60)° = (π/10 800) rad
secondo	″	1″ = (1/60)′ = (π/648 000) rad
litro	l, L	1 L = 1 dm3 = 10-3 m3
tonnellata	t	1 t = 103 kg
neper	Np	1 Np = 1
bel	B	1 B = (1/2) ln 10 (Np)

 

Il neper e il bel esprimono il logaritmo in base e o in base 10 di una grandezza presa rispetto ad un riferimento. Il logaritmo in base 10 dà l’ordine di grandezza in più o in meno rispetto al riferimento ed è quindi usato in Ingegneria molto più spesso di quanto si pensi, spesso involontariamente: se ad esempio pensiamo ad un oggetto un milione di volte più grande di un altro, diciamo che tra i due ci sono 6 ordini di grandezza, cioè 6 bel. La misura logaritmica serve anche a meglio leggere fenomeni a scala fortemente non lineare ed il decibel (dB) serve appunto in molte discipline quali acustica, elettronica, chimica a valutare la crescita (guadagno) o l’attenuazione di una grandezza.

§A1.5 Unità (non apparteneti al SI)  accettate perché più precise.

Nome	Simbolo	Equivalenza in termini di unità fondamentali SI
elettronvolt	eV	1 eV = 1,602 177 33(49) · 10–19 J
unità di massa atomica	u	1 u = 1,660 540 2(10) · 10–27 kg
unità astronomica	ua	1 ua = 1,495 978 70(30) · 1011 m

 

Un elettronvolt (simbolo eV) è l'energia acquistata da un elettrone libero nel suo spostamento tra due punto a potenziale differente per un volt.Un elettronvolt è un quantitativo molto piccolo di energia: 1 eV = 1,602 176 46 × 10-19 J.

L’Unità Astronomica (U.A., o semplicemente UA) è un'unità di misura circa pari alla distanza media tra il pianeta Terra e il Sole

L'unità di massa atomica unificata (u) detta anche dalton (Da) è una unità di misura utilizzata solitamente per esprimere la massa di atomi (massa atomica) e molecole (massa molecolare). Essa è definita come la dodicesima parte della massa di un atomo di carbonio-12 (12C).

A.1.6 Altre unità non SI  accettate in ambiti commerciali, legali, e nella navigazione.
Queste unità dovrebbero essere definite in relazione al SI in ogni documento in cui vengono usate. Il loro uso è scoraggiato.

Nome	Simbolo	Equivalenza in termini di unità fondamentali SI
miglio nautico	nm	1 miglio nautico =1 852 m
nodo	kn	1 nodo = 1 miglio nautico all'ora = (1 852/3 600) m/s
ara	a	1 a = 1 dam2 = 102 m2
ettaro	ha	1 ha = 1 hm2 = 104 m2
bar	bar	1 bar = 0,1 MPa = 100 kPa = 1 000 hPa = 105 Pa
angstrom	Å	1 Å = 0,1 nm = 10-10 m
barn	b	1 b = 100 fm2 = 10-28 m2

 

 

Fonte: http://www.elettrotecnica.unina.it/files/lupo/upload/Elettrotecnica_mat_appendici_1a.doc

Autore del testo: non indicato nel documento di origine

 

Sistema di misura internazionale

Appunti sulla conversione tra il Sistema Tecnico (ST) e il Sistema Internazionale (SI)

 

Fermo restando che l’attuale normativa (direttiva n. 89/617/CEE) obbliga l’uso del Sistema Internazionale dal 31/12/1999 è opportuno conoscere i coefficienti di conversione tra i due sistemi di misura in quanto nell’uso comune è ancora predominante il Sistema Tecnico.

 

Unità di misura fondamentali

Il problema delle conversioni nasce proprio dalla differenze tra le grandezze e le rispettive unità di misura fondamentali tra i due sistemi.
Infatti abbiamo (limitandoci alle unità che interessano la disciplina):

 

SISTEMA INTERNAZIONALE

 

SISTEMA TECNICO

 

Come si può notare la differenza è che nel SI abbiamo come grandezza fondamentale la massa e nel ST il peso che nel SI è invece è una unità derivata.
Infatti nel SI l’unità di misura della forza (e quindi anche del peso) è il newton (N).
Dalla legge di Newton (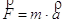 cioè un newton e pari ad una massa unitaria sottoposta all’accelerazione unitaria.
Il problema nasce in quanto nel ST l’unità di misura kg (essendo un peso) implica la presenza dell’accelerazione di gravità (g) che possiamo assumere pari a .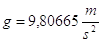
Per maggiore chiarezza chiameremo 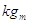 (chilogrammo-peso) l’unità di misura del peso nel ST.

 

Forza

Per passare tra chilogrammi (ST) e newton (N) dobbiamo procedere in questo modo:

l’approssimazione al moltiplicatore 10 non sempre è accettabile soprattutto per valori elevati (es. acciaio).
Analogamente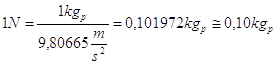

Momento

Essendo il momento il prodotto fra forza e braccio (lunghezza) passeremo tra il chilogrammi per metro (oppure chilogrammetri) ai newton per metro (formalmente dovremo parlare di joule ma nelle Costruzioni tale termine è poco usato) in questo modo:

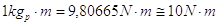
Analogamente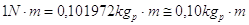

 

Pressione, tensione e modulo di elasticità

Nel ST le tensioni si misurano in 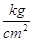 quindi:

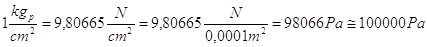
tale valore è troppo grande e si preferisce usare il multiplo MPa (megapascal) essendo 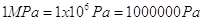 avremo:

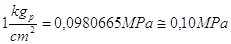
viceversa otterremo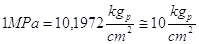
spesso si usa anche il 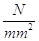 (newton su millimetro quadrato) che corrisponde al MPa

 

Carichi distribuiti

Nel ST i carichi distribuiti si misurano in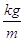
Analogamente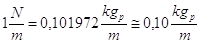
Usando il kN si ottiene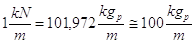

Riassumendo:

I termini tra le parentesi indicano i valori approssimati.

Autore: prof. Gregori Francesco corso di Costruzioni

http://www.itcgap.com/gregori/Conversione%20tra%20SI%20e%20ST.doc

 

Sistema di misura internazionale

BREVE STORIA DELLE UNITA’ DI MISURA E DI COSA E’ STATO FATTO PER UNIFICARLE
In classe abbiamo visto che le unità di misura sono alla base di ogni misurazione. Infatti, misurare significa “vedere quante volte l’unità di misura scelta sta nel campione da misurare”. Perciò, per iniziare a fare Fisica in modo moderno, cioè utilizzando numeri e di conseguenza misure, è necessario fissare delle unità di misura per ogni grandezza fisica. Adesso noi utilizziamo il metro per la lunghezza, il secondo per il tempo, il chilo per la massa… ma è stato sempre così? E se non è stato sempre così, come siamo arrivati a queste unità di misura? Perché sono state scelte proprio queste? E perché sono usate quasi universalmente?

E’ chiaro che le unità di misura sono alla base non solo degli scambi scientifici e tecnici ma anche di quelli commerciali. Nell’antichità, in mancanza di strumenti adeguati, le misure per gli scambi commerciali erano basate su confronti di grandezze unitarie ricavate dalle dimensioni del corpo umano come il piede e il cubito (misura dell’avambraccio) per le lunghezze o utilizzando degli oggetti comuni come l’anfora per le misure di volume o la libbra per i pesi.
A sinistra potete vedere tre unità di misura usate nell'Antico Egitto: due righe per il cubito, di cui una graduata nei suoi sottomultipli, ed un'unità di massa - il deben - equivalente a 93.3 grammi (le foto sono state tratte dal sito "The Weights and Measures of Ancient Egypt" by Jimmy Dunn).
Spesso queste unità di misura avevano lo stesso nome ma valori diversi in Paesi diversi. Lo "stadio", ad esempio, che corrispondeva alla lunghezza della pista per la corsa degli atleti, aveva lunghezza diversa in Egitto e in Grecia. Lo stesso criterio valeva per il "piede", che per Assiri e Babilonesi misurava 32 cm, mentre per gli Egizi era più lungo (34,9 cm).
Ma non occorre andare molto indietro nel tempo né molto lontano nello spazio per farsi un’idea della confusione che creavano le unità di misura diverse in luoghi diversi. Nell’Italia precedente l’unificazione le differenze delle unità di misura fra regione e regione erano notevoli: in Piemonte, ad esempio, per le misure itinerarie si usava il miglio che valeva 2467 metri mentre in Lombardia il miglio, corrispondente a 3000 braccia, valeva 1785 metri. Il caos aumentava passando in Veneto dove ad esempio, per misurare capacità e volumi di merce secca, si usava il moggio (333,3 litri), mentre i liquidi avevano come unità di misura il mastello (75,12 litri); in Piemonte invece i volumi di merce secca venivano espressi in sacchi (115,3 litri) e i liquidi in pinte. La cosa diventava addirittura ingovernabile scendendo lungo la Penisola: pertiche, tornature, carri, quartaroli, corbe da grano o da vino, boccali, imbuti, some e fiaschi erano solo alcune delle unità che si trovavano spostandosi dalla pianura Padana verso la Sicilia.
Cosa dire in campo scientifico? Anche qui regnava l’anarchia: ogni scienziato utilizzava le unità di misura del proprio paese. Leggiamo adesso alcuni brani presi dagli scritti di insigni scienziati del passato: vediamo come essi misuravano le grandezze fisiche durante i loro esperimenti.
Iniziamo da Galileo, riportando una parte del brano che già avete letto in classe, estratto dai “Discorsi e dimostrazioni matematiche intorno a due nuove scienze” (1635), che descrive l’esperimento che Galileo compì sulla caduta dei corpi:
In un regolo, o vogliàn dir corrente, di legno, lungo circa 12 braccia, e largo per un verso mezzo braccio e per l’altro 3 dita, si era in questa minor larghezza incavato un canaletto, poco più largo d’un dito;
E’ evidente che Galileo misura le lunghezze in braccia e in dita. Ma in quegli stessi anni in Francia, un grande scienziato che incontrerete il II anno, Blaise Pascal, misurava le lunghezze in piedi!
Le lunghezze sono anche misurate da un grande scienziato della fine del 1700, Charles Coulomb, che incontrerete al V anno di Fisica. Egli costruì una bilancia per misurare forze debolissime: per fare questo usò un filo molto sottile. Ecco cosa scrive in una nota del 1785:

Il filo d’argento lungo 28 pouce, che forma la sospensione è così fine che il peso di un piede di lunghezza è circa 1/16 di grano.
Le lunghezze sono misurate in pouce (1pouce=27mm) ed in piedi (1 piede=30,48cm). Inoltre egli misura la massa di un oggetto non in chili o in grammi ma in grani (1 grano=0,053 g). Sono queste allora le unità di misura di lunghezza e di massa di quel periodo? No di certo! O meglio, lo sono per Coulomb, che è inglese. Lavoiser, che è francese, usa altre unità di misura. Ecco cosa Lavoisier in persona scrive in una nota del 1783 riguardo al celeberrimo esperimento della bruciatura del mercurio che lo portò ad enunciare la legge di conservazione della massa (egli scrive in terza persona):
Lo scorso Luglio o Agosto M. Lavoisier ha dato all’Accademia una dettagliata descrizione di questo apparato. La quantità di aria infiammabile bruciata in questo esperimento era circa 30 pinte e quella di aria deflogistizzata (cioè già bruciata) da 15 a 18 pinte (1 pinta=0,953 litri). […] Dopo l’esperimento, quasi tutta l’acqua è stata raccolta per mezzo di un imbuto e il suo peso fu trovato essere circa 5 gros [1 gros=3,82].
Ecco infine in che modo un altro grande scienziato, James Prescott Joule che studieremo al IV anno, descrive le misure di un mulinello che utilizzò per alcune esperienze sul calore nel 1845:

 

Le palette si muovono con grande resistenza in un recipiente contenente acqua, cosicché i pesi, ognuno di quattro libbre
[1 libbra=489,5 g] scendono alla bassa velocità di circa un piede al secondo [0,305 m/sec]. L'altezza delle pulegge da terra è di dodici yarde [1 yarda=0,9144 m].

 

Quante unità di misure! E’ chiaro che la confusione in campo scientifico doveva essere grande, soprattutto quando si dovevano confrontare risultati di scienziati in tempi diversi o di diversa nazionalità.
Questo problema fu affrontato per la prima volta nel 1790, al tempo della Rivoluzione Francese, in pieno Illuminismo. Si decise di adottare un’unica unità di misura per la lunghezza che fosse valida per tutti i popoli della Terra, a simboleggiare il fatto che la Scienza doveva essere un modo per unire insieme tutte le Nazioni, secondo l’ideale di fraternité che aveva guidato i Rivoluzionari contro l’Ancient Regime dei Re. L’unità di misura venne scelta definitivamente nel 1799 e fu il metro, praticamente uguale a quello che abbiamo adesso. Napoleone dichiarò: "Le conquiste militari vanno e vengono, ma questo lavoro durerà per sempre". Si sbagliava: il nuovo sistema suscitò una profonda diffidenza e Napoleone fu costretto a restituire ai francesi le unità di misura dell'Ancien Régime.

 

Fu soltanto verso la metà dell'Ottocento che la Francia e via via le altre nazioni, compresa l'Italia, decisero di unificare le loro unità di misura. Nel 1875 una Convenzione internazionale ratificò l’adozione del metro come unità di lunghezza universale e istituì a Sèvres, un sobborgo di Parigi, il Bureau International des Poids et Mesures (l'Ufficio Internazionale dei Pesi e delle Misure), che è ancora oggi la massima autorità nel campo della misura delle grandezze fisiche. Esso non solo fissò il metro come unità di misura della lunghezza ma si preoccupò piuttosto di definire tutte le grandezze fondamentali, in modo che qualunque grandezza fisica potesse essere espressa con le stesse unità di misura da tutti gli scienziati.  L’Ufficio si riunì varie volte sia per definire nuove grandezze fondamentali sia per ridefinire quelle già note in modo più preciso. Nel 1960 esso definì il sistema di misure universali che è usato tutt’oggi: il cosiddetto Sistema Internazionale (S.I.)

Fonte: http://www.liceoagnoletti.it/attivita/attivita_professori/fisicafacile/Documenti/IC_Breve%20storia%20della%20unificazione%20delle%20unit%E0%20di%20misura.doc

 

Sistema di misura internazionale

 

 

Visita la nostra pagina principale

 

Sistema di misura internazionale

 

Termini d' uso e privacy