Matemateci famosi biografie e teoremi

 

---

 

Matemateci famosi biografie e teoremi

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

 

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

 

 

 

 

 

Matemateci famosi biografie e teoremi

DENIS GUEDJ

BIOGRAFIA

Denis Guedj, nato nel 1940 a Sétif, in Algeria, è uno dei matematici più famosi del mondo. Viene particolarmente apprezzato per il suo modo di spiegare i segreti della matematica, utilizzando forme letterarie come il romanzo, il teatro e perfino il cinema. Trasferitosi a Parigi nel 1957 per studiare matematica, partecipa attivamente alla contestazione studentesca del 1968; in quel periodo, grazie alla collaborazione con una serie di giornali, scopre la sua vocazione alla scrittura che lo porterà, nel 1987, a scrivere romanzi, il primo dei quali è Il Meridiano (in Francia insignito del Prix de L'Institut), seguito, nel 1988, da La Révolution des Savants e L'impero dei numeri, apparso anche in Italia nel 1997. Parallelamente alle sue attività di scrittore e d'insegnante - attualmente è docente di Storia delle scienze all'università Paris VIII -, Guedj si è impegnato nel campo del cinema e del teatro, nella convinzione che "anche i concetti possono dare emozioni: per questo li racconto e li 'metto in scena'". E lo straordinario successo in Francia, in Germania e anche in Italia del Teorema del Pappagallo (edito da Longanesi) gli ha dato ragione. Da Longanesi sono apparsi anche Il Meridiano e Autobiografia di una caravella.   

 

RIASSUNTO

Il romanzo è ambientato principalmente a Parigi, nel quartiere di Monmartre, dove vive un libraio filosofo di ottantaquattro anni, il signor Ruche, costretto alla sedia rotelle dopo un incidente. Egli ospita in casa ormai da anni una piccola famiglia, composta da Perette, che gestisce la sua libreria, i figli Jonathan e Lea, gemelli di diciassette anni, e Max, di dodici anni, sordo ma con molte altre qualità e risorse.
Un bel giorno, accadono due avvenimenti che sconvolgono la tranquilla vita in Rue Ravignan: mentre Max salva un pappagallo su cui litigavano degli strani uomini al mercato delle pulci, Il signor Ruche riceve una lettera da un suo vecchio amico, Grosouvre, un matematico con cui aveva condiviso gli anni della guerra, in cui è scritto che presto gli invierà la sua biblioteca di matematica, la più completa del mondo, direttamente da Manaus,dove vive ormai da anni. Questo fatto sconvolge il signor Ruche, poichè credeva l’amico morto, ma comincia a cercare una sistemazione per i libri che presto arriveranno. Intanto, scoprono che il pappagallo non è silenzioso, anzi “racconta” ciò che gli viene riferito; gli viene dato il nome di Nofutur. Arriva la biblioteca, e con essa un’altra lettera di Grosuvre, che contiene terribili rivelazioni: l’uomo infatti, scrive di aver risolto due enigmi della matematica, ma di non voler rivelare a nessuno le soluzioni, a eccetto che a un “fedele compagno”, poichè degli uomini vogliono estorcergliele, anche con la forza. Un allegato alla lettera è invece della polizia di Manaus, in cui è affermato che Grosouvre sarebbe morto poco dopo in un incendio che ha colpito la sua proprietà. Da qui, comincia un lungo viaggio attraverso la matematica, un percorso durante il quale il signor Ruche cerca di scoprire i segreti dell’amico, grazie a delle citazioni di matematici lasciate nella lettera, e cosi riesce ad appassionarsi a un argomento che fino a quel momento non lo sfiorava affatto, capendo invece che matematica e filosofia viaggiano su binari paralleli, e non c’è niente di scontato, niente di “solo razionale”. Cominciano le cosiddette “sedute” in Rue Ravignan, durante le quali gli attori, Max, il signor Ruche e Nofutur, raccontano al resto della famiglia le storie dei matematici di tutti i tempi.
La soluzione della vicenda era molto più vicina di quanto tutti si aspettassero, e un finale mozzafiato conclude l’appassionante romanzo: dopo la scomparsa di Nofutur, un bel giorno Max viene rapito, e una telefonata informa che il bambino sta bene, ed è in Sicilia; richiesta arrivo del signor Ruche. Questo parte subito, e giunto in Sicilia scopre che il rapitore è un vecchio amico suo e di Grosuvre, Tavio, e che il pappagallo è lì. Finalmente gli viene spiegato il mistero: Tavio, era giunto a Manaus e aveva incontrato Grosouvre, ed aveva scoperto che egli aveva risolto le dimostrazioni; quello che chiedeva era condividerle con lui, senza rivelarne il contenuto. Ma l’uomo non aveva nessuna intenzione di farlo, e aveva “raccontato” le soluzioni al suo compagno fedele da quarant’anni: NOFUTUR! La sera dell’incendio Tavio aspettava la risposta definitiva dell’amico, ma giunto a casa sua, tutto era già in fiamme. Avendo capito che il pappagallo conosceva ogni cosa, cercò di appropriarsene, ma questo era finito nelle mani di trafficanti di animali che lo avevano portato a Parigi, dove lo aveva trovato Max. Ora, però, Nofutur, aveva perso la memoria: cercano in tutti i modi di fargliela tornare, addirittura vanno a Manaus, perchè per il signor Ruche la cosa importante era portare a casa Max, e Tavio, boss della mafia, non li avrebbe lasciati andare se almeno non avessero tentato ogni strada. Ma tutto è vano, anzi, Tavio muore in Amazzonia per un attacco di cuore nel momento in cui uno dei suoi spara a Nofutur per la rabbia. Solo Max lo vede rispuntare tra gli alberi, e capisce che si è salvato. Ma un altro segreto viene svelato, e anche questo, come molti altri in questa storia, viene nascosto in una sola persona: il signor Ruche trova un foglio che Tavio gli ha scritto prima di morire, in cui dice che Grosouvre, nell’incendio, si è forse salvato... 

 

 

TALETE MISURA LA PIRAMIDE

 

In terra d’Egitto, Talete sbalordisce tutti, agrimensori, sacerdoti e il re: misura la piramide, la tomba del re. Il successo è pieno e totale e Plutarco così lo riporta: " [Il re] è rimasto singolarmente ben impressionato dal modo in cui hai misurato la piramide, [...], limitandoti a collocare il tuo bastone al limite dell’ombra proiettata dalla piramide stessa; formatisi, al contatto col sole, due triangoli, dimostrasti che la proporzione esistente fra la lunghezza del bastone e l’altezza della piramide era la stessa che intercorreva fra la lunghezza delle due ombre. Ciò nonostante .... ti si muove l’accusa d’avere in odio i re".
Poiché i raggi del sole sono paralleli, i triangoli AOA' e VHV' sono simili e, come l'ombra del bastone è doppia della sua altezza, così l'ombra della piramide sarà doppia rispetto alla sua altezza.
E' questa un'importante applicazione del teorema di Talete: la sua formulazione è forse nata dall'osservazione dei raggi del sole. Questi,  incontrando i corpi materiali, vengono fermati, e si formano delle ombre.

Osservando tali ombre si può notare che nel corso della giornata queste variano ma, pur variando, si nota che qualcosa rimane immutato:

• i segmenti AB e BC, che sono uguali, si trasformano nei segmenti A'B' e C'D' che restano sempre uguali fra di loro;
• AC = 2AB, si trasforma in A'C' = 2AC, ossia il rapporto fra segmenti corrispondenti non muta.

 

 

PITAGORA

BIOGRAFIA

Pitagora nacque a Samo verso il 572 a.C. da Mnesarco, ricco gioielliere, e Pitaide, considerata la più bella donna dell’isola. Secondo l’oracolo di Delfi fu per opera del dio Apollo che ella rimase incinta e mise al mondo “un figlio di straordinaria bellezza e d’una intelligenza superiore a quella di tutti i tempi”.
Si attribuisce alla sua adolescenza la famosa tavola che riassume le operazioni di moltiplicazione e divisione dei numeri dall’1 al 10 e il teorema secondo il quale “in ogni triangolo rettangolo il quadrato costruito sull’ipotenusa è uguale alla somma dei quadrati costruiti sui cateti” che aveva appreso “da quei popoli che per civiltà e cultura avevano preceduto la Grecia”. Infatti molto tempo prima di lui gli egizi e soprattutto i babilonesi avevano scoperto che esisteva un legame tra alcuni gruppi di tre numeri interi, e precisamente qullo indicato dal celebre teorema; inoltre anche in un antichissimo esemplare di stampa a caratteri mobili cinesi del 1000 a.C., “Il libro di Chou Pei Suan King”, questo teorema era già trattato.
Pitagora aveva diciotto anni quando partecipò alle Olimpiadi vincendo le gare di pugilato. Dopo la vittoria, decise di viaggiare allo scopo di perfezionare la sua cultura.
Dapprima giunse a Lesbo dove seguì l'insegnamento di Ferecide da Siro; partecipò alla scuola di Anassimandro; in seguito si trasferì a Mileto sotto la guida del più celebre sapiente dell'epoca, Talete, detto "uno dei Sette Savi".
Si dice che Pitagora, chiamato per la sua bellezza “il Samio dai lunghi capelli", impressionò lo stesso maestro col suo precoce sapere a tal punto che Talete si mise a studiare le scoperte geometriche del suo allievo.
Pitagora si recò poi in Fenicia, visitò Sidone, il tempio di Adonai, si fece iniziare ai misteri di Tiro, di Biblos e di altri santuari della Siria, poi si ritirò per qualche tempo nel tempio fenicio del Monte Carmelo.
Si racconta che un giorno dalla vetta del Carmelo, Pitagora vide nella baia sottostante una nave egiziana in procinto di salpare; subito si precipitò, attraversando pendii, rocce e precipizi, facendo segno ai marinai di attenderlo. Giunto sulla riva salì a bordo e si pose in un angolo della nave.
Per tutto il viaggio, di due notti e tre giorni, rimase sempre nella stessa posizione, senza mangiare né dormire.
I marinai egizi, dapprima incuriositi e poi intimoriti dallo strano personaggio che pareva assorto in una visione sovrumana, quando accostarono sulle rive del Nilo improvvisarono un altare e gli offrirono doni e frutti.
Il suo soggiorno in Egitto non prese l'avvio sperato. Infatti i  sacerdoti non erano disposti a rivelare allo straniero gli arcani del loro sapere. Più volte fu rifiutato, sia a Menfi che a Eliopoli. Poi, dietro insistenti spinte del Faraone Amasi, i sacerdoti di Tebe lo accettarono imponendogli comunque un durissimo noviziato.
Lui affrontò tutte le prove con coraggio e i sacerdoti lo ammisero alle cerimonie del loro culto, il che non era ancora avvenuto per nessun straniero. La sua iniziazione durò ben 22 anni.
Quando i persiani invasero il paese lui si ritrovò prigioniero e venne condotto a Babilonia dove, in quel periodo, dominavano principalmente tre correnti religiose: l'antico sacerdozio caldeo, il magismo persiano e il giudaismo. Pitagora ebbe così modo di studiare a fondo e penetrare negli arcani dell'antica magia, patrimonio degli iniziati persiani, di apprendere dai Caldei l'astronomia, l'astrologia e la medicina, e fu pure favorito dall'incontro con Zoroastro che gli permise di studiare anche le religioni dell'India, proprio nell'epoca in cui il Buddha cominciava la sua rivoluzione religiosa. Venne iniziato ai misteri di Zarathustra e da lui ricevette direttamente l'iniziazione presso le acque dell'Eufrate.
Dopo 12 anni tornò a Samo. Qui però regnava il tiranno Policrate e lui, odiandi i tiranni, ripartì. Sbarcò a Sibari, famosa per essere una città dedita a ogni forma di piacere, e infine si stabilì nella vicina città di Crotone, dove fondo la sua celebre scuola.
Pitagora fu cacciato da Crotone con i suoi seguaci sul finire del VI secolo, in seguito a una sommossa di democratici. Si rifugiò allora a Metaponto, dove morì. Col passare degli anni, numerose leggende ammantarono sempre più la sua figura di un'aura religiosa, facendone una sorta di dio in terra.
Dal gruppo originario derivarono, in numerose città dell'antica Grecia, varie comunità pitagoriche, tra cui spiccano la scuola di Filolao, prima in Magna Grecia e poi a Tebe (V sec.), e quella di Archita a Taranto (inizio del IV sec.). Altri pitagorici furono Simmia e Cebete.

I PITAGORICI

 

PENSIERO

All’inizio i pitagorici erano visti e trattati come una setta poiché seguaci dell “Orfismo”. Questa dottrina viene dagli Orfici ed afferma che il fine della vita è quello di liberare l’anima dal corpo, e per raggiungere tale fine occorre purificarsi. Successivamente però questa comunità divenne una vera e propria “scuola di pensiero”, sotto la guida del suo fondatore, Pitagora.
Punto focale della società pitagorica era il considerare gli studi filosofici e matematici fondamenti della vita morale di ciascuno. Si suppone infatti che Pitagora coniò i termini  filosofia (amore della saggezza) e Matematica (ciò che si impara) per descrivere la propria attività intellettuale. Inoltre secondo i pitagorici i numeri sono il principio di tutte le cose poiché per conoscere la realtà una persona deve riuscire a quantificarla e a misurarla: il mezzo per fare ciò era appunto il numero. L’importanza dei numeri e della matematica si trova anche nel motto della scuola pitagorica: “Tutto è un numero”; Pitagora indicò infatti i numeri con dei sassolini o puntini e si accorse che, messi uno dopo l’altro, costituivano una linea e successivamente l’insieme delle linee formavano una forma. Così il numero si presentò come l’essenza di tutte le cose; in questo modo l’intero universo è armonia e numero. È dei Pitagorici l’idea che i cieli, ruotando appunto secondo armonia e numero producano dei suoni; per ogni sfera vi è un tono musicale e l’ottava musicale è l’insieme di questi toni.
Pitagora distinse inoltre i numeri in pari e dispari. I pitagorici credevano che il pari fosse simbolo di imperfezione mentre il dispari simbolo di perfezione.
Infatti se raffiguriamo in questo modo un numero pari e facciamo passare una retta nel mezzo essa non avrà fine e sarà perciò imperfetta per la mente umana:

                                                                            *
 

                                                                            *
Mentre se raffiguriamo in questo modo un numero dispari e facciamo passare una retta nel mezzo essa avrà una fine e sarà perfetta per la mente umana che sarà in grado di visualizzarla:

 

*
                                                                        *
*

 

L’opposizione pari-dispari è principio di altre nove opposizioni, citate da Aristotele: limitato-illimitato, uno-molti, destra-sinistra, maschio-femmina, bene-male, ecc.
Particolarmente importante per i pitagorici era il numero 10, il numero perfetto,spesso denominato “sacro”, poiché contiene in sé i primi quattro interi (1+2+3+4=10) e perché 10 punti, opportunamente disposti, formano un triangolo perfetto (il cosiddetto Tetraktys), simbolo della scuola pitagorica.
I numeri Pitagorici sono numeri interi, collezioni di più unità, ciascuna rappresentata con un punto circondato da uno spazio vuoto. Una caratteristica della matematica pitagorica è perciò la cosiddetta discontinuità. Infatti essa non conosce le grandezze incommensurabili, i numeri irrazionali: poiché ad una grandezza non si può aggiungere qualcosa che sia minore di un’unità, il suo accrescimento avviene per “salti discontinui”. Fu però proprio il teorema di Pitagora che pose in crisi il pitagorismo, perché portò alla scoperta delle grandezze incommensurabili. Infatti mediante la sua applicazione a uno dei due triangoli isosceli in cui è diviso un quadrato risulta che lato e diagonale del quadrato sono tra loro incommensurabili.

 

CONTRIBUTI ALLA MATEMATICA E NON SOLO

A Pitagora e ai pitagorici, si devono le seguenti scoperte:

• La somma degli angoli interni di un triangolo è pari a due angoli retti (180°).
• La somma degli angoli esterni di un qualunque poligono convesso vale sempre 360°.

 

• Il noto teorema che afferma che il quadrato costruito sull’ipotenusa è pari alla somma dei quadrati costruiti sui cateti.

• I cinque solidi regolari, studiati in seguito anche da Platone: il tetraedro, l’esaedro, l’ottaedro, l’icosaedro e il dodecaedro.

 

• La scoperta dei numeri irrazionali.

• Lo studio di alcuni particolari numeri assieme alle loro proprietà: numeri primi, numeri poligonali, numeri amicali.

 

A queste si aggiungono le scoperte dei pitagorici che, comunque, spaziano in molti altri campi. Per esempio:

• In campo musicale, Pitagora scoprì i rapporti che legano le note musicali. Si dice infatti che ascoltando dei fabbri battere sulle incudini, egli notò che i suoni prodotti erano consonanti o dissonanti a seconda dei pesi dei martelli usati.

 

• In campo astronomicoPitagora scoprì che i due astri Espero e Fosforo, così chiamati dai greci in quanto erano visibili in cielo alla sera e al mattino, prima dell'alba, erano in realtà lo stesso astro (il pianeta Venere).

 

Il TEOREMA DI PITAGORA

In ogni triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti

  

 

 

Dato il triangolo rettangolo ABC costruisco sui cateti i 2 quadrati rispettivamente di lato AC e CB e sull’ipotenusa il quadrato di lato AB.
Conduco dal punto C la perpendicolare al lato AB e la prolungo fino ad incontrare il lato MI nel punto L.
Per il primo teorema di Euclide (in ogni triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo avente per dimensioni la proiezione del cateto stesso sull’ipotenusa e l’ipotenusa) applicato sul triangolo rettangolo AHC, il quadrato ACDE e equivalente al rettangolo AHLM; per lo stesso teorema applicato sul triangolo rettangolo CHB, il quadrato di lato CB è equivalente al rettangolo HBIL.
Poiché il quadrato costruito sull’ipotenusa è uguale alla somma dei rettangoli AHLM e HBIL, resta effettivamente provato che la somma dei quadrati costruiti sui cateti è equivalente al quadrato dell’ipotenusa.

Essendo il teorema uno dei più noti della storia della matematica, ne esistono molte altre dimostrazioni, opera di astronomi, agenti di cambio, e anche una di Leonardo da Vinci.
Ecco quella proposta nel 1873 dall'agente di cambio Henry Perigal:

 

 

 

 

 

Essa si basa sulla scomposizione del quadrato costruito sul cateto maggiore, in giallo nell'immagine: tagliandolo infatti con due rette passanti per il suo centro, una perpendicolare ed una parallela all'ipotenusa, si può ricomporre in maniera da incorporare l'altro quadrato, e formando il quadrato sull'ipotenusa, come nella figura.

I NUMERI IRRAZIONALI

 

CENNI STORICI

La scoperta dei numeri irrazionali viene tradizionalmente attribuita a Pitagora, o più precisamente al pitagorico Ippaso di Metaponto, che produsse una argomentazione (probabilmente con considerazioni geometriche) dell'irrazionalità della radice quadrata di 2. Secondo la tradizione Ippaso scoprì i numeri irrazionali mentre tentava di rappresentare la radice quadrata di 2 come frazione .Tuttavia Pitagora credeva nell'assolutezza dei numeri, e non poteva accettare l'esistenza dei numeri irrazionali. Egli non era in grado di confutare la loro esistenza con la logica, ma le sue credenze non potevano tollerarne l'esistenza e, secondo una leggenda, per questo condannò Ippaso a morire annegato.
Le frazioni continue, strettamente collegate ai numeri irrazionali (e dovute a Cataldi, 1613), furono prese in considerazione da parte di Eulero, e all'inizio del diciannovesimo secolo ebbero maggior rilievo grazie agli scritti di Joseph Louis Lagrange. Altri notevoli contributi furono dati da Druckenmüller (1837), Kunze (1857), Lemke (1870) e Günther (1872). Peter Ramus (1855) per la prima volta collegò l'argomento con i determinanti, dando vita, con i successivi contributi di Heine, August Ferdinand Möbius e Günther, alla teoria dei determinanti delle frazioni continue. Anche Dirichlet contribuì alla teoria generale.
I numeri trascendenti furono per la prima volta distinti dagli irrazionali algebrici da Kronecker. Lambert provò (1761) che π non può essere razionale, e che en è irrazionale se n è razionale (eccetto n = 0), dimostrazione, comunque, che lasciò molto a desiderare. Legendre (1794) completò la dimostrazione di Lambert, e mostrò che π non è la radice quadrata di un numero razionale. Joseph Liouville (1840) mostrò che né e né e2 possono essere radici di un'equazione quadratica intera. Ma l'esistenza di numeri trascendenti fu per la prima volta stabilita da Liouville (1844, 1851); la sua dimostrazione fu successivamente rimpiazzata da Georg Cantor (1873). Charles Hermite (1873) provò per primo la trascendenza di e, e Ferdinand von Lindemann (1882), partendo dalle conclusioni di Hermite, mostrò lo stesso per π. La dimostrazione di Lindemann fu molto semplificata da Weierstrass (1885), e ulteriormente da David Hilbert (1893); infine fu resa quasi elementare da Hurwitz e Gordan.

L’IRRAZIONALITA’ DELLA RADICE DI 2

Una dimostrazione dell'irrazionalità della radice quadrata di 2 è la seguente, che procede per assurdo. La proposizione è provata assumendo l'opposto e mostrando che è falso, che implica che la proposizione iniziale debba essere vera.

1. Assumiamo che .
2. Allora .
3. Segue che    .
4. Dunque a2 è pari perché è uguale a 2b2 che è ovviamente pari.
5. Segue che anche a deve essere pari. (Infatti numeri dispari hanno quadrati dispari e numeri pari hanno quadrati pari.)
6. Poiché a è pari, esiste un intero k che soddisfa: a = 2k.
7. Sostituendo otteniamo: 2b2 = (2k)2, cioè b2 = 2k2.
8. Poiché 2k2 è pari segue che anche b2 è pari e quindi anche b è pari.
9. In base alla (5) e la (8) a e b sono entrambi pari, che contraddice il fatto che sia irriducibile come supposto nella (2).

NUMERI DI CUI NON SI E’ ACCETTATA L’IRRAZIONALITA’

Non si sa ancora se π + e o π − e siano irrazionali o no. Infatti, non c'è nessuna coppia di interi non nulli m ed n per cui si sappia se mπ + ne è irrazionale o no. Non si sa neanche se 2e, πe, o la costante di Eulero-Mascheroni siano irrazionali.

L’INSIEME DI TUTTI I NUMERI IRRAZIONALI

L'insieme di tutti i numeri irrazionali non è numerabile (poiché i razionali sono numerabili e i reali non lo sono). L'insieme degli irrazionali algebrici, ossia gli irrazionali non-trascendenti, è numerabile. Usando il valore assoluto per misurare le distanze, i numeri irrazionali diventano uno spazio metrico che non è completo. Tuttavia, questo spazio metrico è omeomorfo allo spazio metrico completo di tutte le sequenze di interi positivi; l'omomorfismo è dato dall'espansione in frazione continua infinita.

 

EUCLIDE

 

BIOGRAFIA

Euclide nacque probabilmente attorno al 259 a.C., studiò ad Atene e fu il fondatore della scuola matematica di Alessandria. Euclide sta tra i grandi nomi della storia della matematica essenzialmente per aver scritto gli Elementi. Quest’opera ha avuto un’influenza enorme su tutto il pensiero occidentale: è stata studiata, analizzata, e commentata secolo dopo secolo, fino all’epoca moderna. Di tutti i libri della civiltà occidentale solo la Bibbia, s’è detto, è stata studiata più a fondo del testo di Euclide.
I tanto celebrati  Elementi non sono altro, in realtà, che un’enorme raccolta ( divisa in 13 libri) di 465 proposizioni di geometria, piana e solida, e di teoria dei numeri. In generale oggi si ritiene però che solo pochi di questi teoremi siano dovuti personalmente a Euclide; il suo grande merito fu piuttosto quello di organizzare tutto il sapere matematico del tempo in un trattato così ben progettato e di così grande successo da oscurare ogni precedente opera dello stesso genere.
Gli Elementi non sono semplicemente una raccolta di teoremi con le relative dimostrazioni: l’opera, infatti, ha come base 23 definizioni, 5 postulati e 5 “nozioni comuni” o assiomi generali. Partendo da questi fondamenti Euclide dimostrò la sua prima proposizione. Certamente Euclide non sempre riuscì a seguire scrupolosamente il proprio metodo e i suoi ragionamenti non sono esenti da difetti ; tuttavia gli Elementi rappresentano un modello per tutto il lavoro matematico successivo.

I TEOREMI DI EUCLIDE

Solo nei tredici libri degli Elementi Euclide enuncia e dimostra 465 proposizioni e teoremi, senza contare i lemmi o corollari. I due teoremi che vengono comunemente denominati primo e secondo teorema di Euclide, sono in realtà dei corollari della proposizione 8 del VI libro degli Elementi :
“Se in un triangolo rettangolo si conduce la perpendicolare all’angolo retto alla base i triangoli così formati saranno simili al dato, e simili tra loro.”
I due corollari sono così enunciati

PRIMO TEOREMA DI EUCLIDE

“ In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo avente per dimensioni l’ipotenusa e la proiezione del cateto sull’ipotenusa”.
Dimostrazione:

 

 

 

Soggetto: ABC
Ipotesi: CBA 90°
Tesi: CHLM = BCDE

Si costruisca quindi il quadrato BCDE sopra il cateto BC, quindi sul prolungamento di BH dalla parte di H si prenda un segmento HM=AC e si completi il rettangolo aventeper lati CH, HM, che è manifestatamente il rettangolo avente per dimensioni l’ipotenusa e la proiezione del cateto BC su di essa. Si prolunghino i lati HM e CL del rettangolo fino ad incontrare rispettivamente in F e in G la retta EG e si osservi che il quadrilatero FGCB è un parallelogrammo, perché ha i lati opposti paralleli.

Si considerino ora i due triangoli rettangoli ABC e CEF: essi sono congruenti perché hanno i due catei CB , CE congruenti come lati di un quadrato e gli angoli acuti BCA, BCE congruenti perché complementari  dello stesso angolo FCA (criterio di congruenza dei triangoli).
Dalla congruenza di questi due angoli si deduce che CF è congruente a CA, ma siccome CA è congruente a CL, sarà anche CL congruente a CF. Allora il triangolo CHLM e il parallelogrammo FGBC sono equivalenti perché hanno le basi AN,AL congruenti e la stessa AH. Ma il parallelogrammo FGBC risulta equivalente al quadrato BCDE perché ha la stessa base BC e la stessa altezza CE: quindi per proprietà transitiva, il rettangolo CHLM è equivalente al quadrato BCDE.

SECONDO TEOREMA DI EUCLIDE

 

“ In ogni triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull’ipotenusa”.

 

Dimostrazione:

 

 

 

Soggetto: ABC
Ipotesi: BCA 90°
AH perpendicolare a BC
Tesi : RSLM = BHQP

Dopo aver costruito il quadrato BHQP su BH si costruisca il rettangolo CHLM con CL = AC e CH = BC si prenda su HM un punto S il modo che sia HS = CH per il teorema di Pitagora sarà CHSR + BHQP = BCDE, ma per il primo teorema di Euclide sarà anche CHLM = BCDE. Per proprietà transitiva sarà poi CHSR + BHQP = CHLM, ma siccome CHLM = RSLM + CHRS, l’equivalenza sarà CHSR + BHQP = RSLM + CHSR, cioè BHQP = RSLM.

GLI ASSIOMI DI EUCLIDE

 

Tutta la geometria di Euclide si basa su cinque postulati :

• E’ sempre possibile tracciare una retta tra due punti qualunque;
• E’ sempre possibile prolungare una linea retta;
• E’ sempre possibile costruire una circonferenza di raggio qualunque;
• Tutti gli angoli retti sono tra loro congruenti;
• Data una retta ed un punto esterno ad essa esiste un’unica retta parallela passante per detto punto.

 

LE CONICHE

 

Chiamiamo conica quella curva che si ottiene intersecando un cono rotondo indefinito con un piano non passante per il vertice del cono.

Storicamente i primi a studiare le coniche furono i greci, che però le studiarono solo dal esclusivamente dal punto di vista geometrico, cioè come intersezioni di coni con piani.
Lo studioso che però rivoluzionò lo studio delle coniche fu Apollonio di Perga ( o Apollonio di Perge). Egli nacque a Perga nel 262 a.C .
Solo due sue opere sono giunte fino a noi:

• Separazione di un rapporto;
• Coniche ( opera in otto libri, quattro che ci sono giunti nella versione originale greca, tre in traduzione araba. L’ultimo è andato perduto ma è stato ricostruito in modo deduttivo dal matematico arabo Alhazad).

 

CONICHE

Quando Apollonio compose questo celebre trattato le sezioni coniche erano già note da un secolo e mezzo, ma nessuna opera precedente aveva raggiunto un livello così alto. L’autore considerò i primi quattro libri una traduzione elementare e perciò si è avanzata l’ipotesi che gran parte del loro contenuto fosse già apparso in precedenti trattati. Gli ultimi quattro libri  vengono descritti da Apollonio come ulteriori sviluppi degli argomenti al di là degli elementi essenziali.
Prima  di Apollonio l’ellisse , la parabola e l’iperbole venivano come sezioni di tre tipi nettamente distinti di coni circolari retti, a seconda che l’angolo al vertice fosse acuto, retto i ottuso.
Apollonio, per la prima volta, dimostrò che non era  necessario prendere sezioni perpendicolari ad un elemento del cono e che da un unico cono era possibile ottenere tutte e tre le varietà di sezioni coniche semplicemente  variando l’inclinazione del piano d’intersezione. Una seconda importante generalizzazione si ebbe quando Apollonio dimostrò che non era necessario che il cono fosse retto
( cioè un cono il cui asse è perpendicolare alla base), ma che poteva essere anche u  cono circolare obliquo o scaleno. Infine, Apollonio avvicinò ulteriormente le antiche curve al punto di vista moderno sostituendo il cono a una falda con un cono a doppia falda. Infatti, Apollonio dava la stessa definizione che viene usata ancora oggi di cono circolare:
Se una retta, prolungatesi all’infinito e passante per un punto fisso, viene fatta ruotare lungo la circonferenza di un cerchio che non si trovi nello stesso piano del punto in modo che passi successivamente attraverso ogni punto di quella circonferenza, la retta che ruota traccerà la superficie di un cono doppio.

Fu Apollonio a introdurre i termini “ellisse”, “iperbole” e “parabola” in relazione alle sezioni coniche: essi rappresentavano adattamenti di termini che erano già statiusati in precedenza nella soluzione delle equazioni di secondo grado mediante l’applicazione di aree.
E’ stata fatta congettura che il libro VIII, perduto, delle Coniche non facesse che continuare la trattazione di problemi simili: infatti nella prefazione del libro VII l’autore scriveva che i teoremi di tale libro sarebbero stati usati nell’ottavo per risolvere i problemi conici, così che l’ultimo è una sorta di appendice.

 SEZIONE DI UN RAPPORTO

Nonostante la sua enorme produzione scientifica, solo un altro tra i numerosi trattati di Apollonio è pervenuto in forma quasi completa. Tutte le versioni greche della Sezione di un rapporto andarono perdute molto tempo fa, ma non prima che fosse stata fatta una traduzione araba. Essa tratta vari casi di un problema generale: date due rette e un punto su ciascuna di esse, tracciare per un terzo punto dato una retta che intersechi sulle rette date segmenti ( misurati a partire dai punti fissi rispettivamente giacenti si di esse) che siano in un dato rapporto.

Attraverso le descrizioni fornite di commentatori posteriori, conosciamo il titolo di molte opere perdute:

• Sezioni di un’area

Il problema trattato è simile a quello della Sezione di un rapporto, tranne che i segmenti intersecati devono delimitare un dato rettangolo, piuttosto che essere in un dato rapporto. Questo problema porta alla costruzione, su un segmento a, di unrettangolo uguale a un rettangolo più un quadrato.

• Sulla sezione determinata

Tratta quella che potremmo chiamare geometria analitica ad una dimensione. Esso considera il seguente problema generale: dati quattro punti A,B,C,D, giacenti su una retta, determinare il quinto punto P giacente su di essa tale che il rettangolo delimitato dai segmenti AP e CP stia in un dato rapporto con il rettangolo delimitato dai segmenti BO e DP.

• Tangenze

Presenta il problema noto come il Problema di Apollonio. Date tre cose, ciascuna delle quali può essere un punto, una retta o un cerchio, tracciare un cerchio che sia tangente a ciascuna delle tre cose. Questo problema comporta dieci casi, dai due più facili in cui le tre cose sono tre punti o tre rette a quello più difficile in cui le tre cose sono tre cerchi.

• Inclinazioni

Apollonio considerava la classe dei problemi di neusis (inclinazione) che potevano essere risolti con metodi “piani”, ossia solo per mezzo di riga e compasso.

• Luoghi Piani

Tra alcuni luoghi considerati vi erano: il luogo dei punti tali che la differenza dei quadrati delle loro distanze da due punti fissi sia costante, è una retta perpendicolare al segmento che congiunge i punti; il luogo dei punti tali che il rapporto delle loro distanze da due punti fissi sia costante ( e diverso da uno) è un cerchio. Quest’ultimo luogo è oggi noto come Cerchio di Apollonio.

 

NICCOLO’ TARTAGLIA

 

BIOGRAFIA

Niccolò Fontana (Brescia,  1499 circa – Venezia,  13 dicembre 1557) è stato un matematico italiano, noto con il soprannome e lo pseudonimo di Niccolò Tartaglia; il cui nome è legato al noto triangolo. // if (window.showTocToggle) { var tocShowText = "mostra"; var tocHideText = "nascondi"; showTocToggle(); } //
Nacque da una famiglia poverissima. Durante la presa di Brescia da parte dei francesi nel 1512 il padre fu ucciso e lui stesso ferito alla mandibola e al palato. Dato per morto, sopravvisse grazie alle cure della madre, ma gli rimase un’evidente difficoltà ad articolare le parole. Per questo ebbe il soprannome "Tartaglia" che accettò e utilizzò tutta la vita per firmare le sue opere.
Non poté frequentare alcuna scuola da giovane ed era molto fiero d’essere autodidatta. Nei suoi scritti, si vanta, infatti, di essere andato a scuola di scrittura solo per 15 giorni, all'età di 14 anni. Grazie alla sua abilità, poté lo stesso guadagnarsi da vivere a Verona risolvendo l'equazione cubica o equazione di terzo grado. In realtà la formula era stata trovata, ma non pubblicata, da Scipione Dal Ferro nei primi del 1500, e fu nuovamente inventata dal Tartaglia una ventina di anni dopo, mentre sullo stesso problema lavoravano anche il professor Gerolamo Cardano e il suo discepolo Ludovico Ferrari più o meno nello stesso periodo.
A Tartaglia dobbiamo tra l'altro la prima traduzione italiana degli Elementi di Euclide.
In un trattato Quesiti e inventioni diverse s’interessa anche di balistica e di fortificazioni.

 

L’INVENZIONE DELLA FORMULA RISOLUTIVA DELL’EQUAZIONE CUBICA

Il primo matematico che arrivò ad una formula risolutiva per le equazioni di terzo grado fu Scipione Dal Ferro: la sua formula era generale perché tutte le cubiche sono riconducibili a questa tramite la sostituzione dove b è il coefficiente di secondo grado. Di fatto, a quel tempo non erano stati studiati ancora i numeri negativi, i numeri immaginari non erano ancora stati inventati, e neanche il piano cartesiano; infine anche la relazione fra il numero di radici e il grado dell’equazione non era stata ancora dimostrata.
In più, accadeva a quel tempo che i matematici custodissero gelosamente le proprie scoperte, oppure le rendessero note solo ad una stretta cerchia di amici o discepoli; altre volte, enunciato un principio, omettevano di pubblicare parte o tutta la dimostrazione. Fu così che Dal Ferro non pubblicò la formula risolutiva, ma la lasciò ad un suo allievo fidato, ma non molto geniale, Antonio Maria del Fiore, che dopo anni cominciò a vantarsi della propria capacità di risolvere le equazioni cubiche. Questo stimolò il Tartaglia che, in maniera indipendente, riscoprì la formula di Dal Ferro e, nel febbraio del 1535, accettò una cartello di matematica disfida dello stesso Fiore.
La disfida era un evento pubblico in cui ciascuno degli sfidanti sottoponeva all'altro problemi di vario tipo, depositandoli da un notaio e distribuendoli ai testimoni; il vincitore veniva deciso da giudici scelti di comune accordo. In questo caso particolare, Tartaglia risolse tutti i problemi posti da Fiore in due ore, mentre questi non ne risolse alcuno fra quelli posti da Tartaglia; la disfida si concluse dunque con un pieno successo di Tartaglia.
L'evento ebbe larga risonanza, e Niccolò Tartaglia fu oggetto di attenzioni da parte di Gerolamo Cardano, che nel marzo del 1539 lo invitò a Milano, dove era introdotto abbastanza bene, e si fece confidare la famosa formula, dietro la promessa che non ne avrebbe parlato ad alcuno. Probabilmente Tartaglia si era mosso da Venezia con la speranza di ottenere una qualche introduzione nel mondo accademico milanese, che invece non arrivò.
Cardano, con l'aiuto del suo allievo Ludovico Ferrari, approfondì le formule dell'equazione cubica e la migliorò, trovandone una anche per il caso generale. Il Tartaglia non si decideva a pubblicare i suoi risultati; e qualche anno dopo il Cardano, con l'aiuto di Fiore, scoprì da alcune carte che erano in possesso del genero di Dal Ferro che la formula era stata inventata anche da quest'ultimo. Pertanto si ritenne libero dalla promessa fatta al Tartaglia e si decise a comprendere i suoi risultati nell' Ars Magna che pubblicò nel 1545, ben sapendo che avrebbe così suscitato le ire di Tartaglia, così come di fatto avvenne.
Nel 1546 infatti Tartaglia pubblicò la sua opera "Quesiti et Inventioni diverse" dove, con parole offensive verso Cardano, denunciava la violazione del giuramento fattogli; il Ferrari, in difesa del suo amico e professore, lanciò il primo cartello di disfida contro Tartaglia, seguito da altri cinque nel giro di due anni. Tartaglia, per le sue difficoltà di parola, intendeva disputare per iscritto, Ferrari invece insisteva per uno scontro verbale e per tenere la disputa a Milano, dove lui poteva contare su amicizie e conoscenze. L'ultimo scontro si concluse il 10 agosto 1548; a Tartaglia non fu permesso di esporre le proprie ragioni e per questo motivo il giorno seguente ritornò a Brescia, dove si era trasferito da poco.
Gli scontri non ebbero esito positivo per Tartaglia, che perse anche il lavoro a Brescia, ebbe difficoltà finanziarie e dovette far ritorno poco dopo a Venezia. Comunque i posteri hanno riconosciuto a Cardano parte della paternità dell'invenzione della formula risolutiva dell'equazione cubica, chiamandola formula di Cardano-Tartaglia.

 

FIBONACCI

 

BIOGRAFIA

Leonardo Fibonacci, figlio di Guglielmo Bonacci, nacque a Pisa intorno al 1170. Suo padre era segretario della Repubblica di Pisa e responsabile a partire dal 1192 del commercio pisano presso la colonia di Bugia, in Algeria. Alcuni anni dopo il 1192, Bonacci portò suo figlio con lui a Bugia. Il padre , poiché voleva che Leonardo divenisse un mercante, provvedette alla sua istruzione nelle tecniche del calcolo, specialmente quelle che riguardavano le cifre indo-arabiche, che non erano ancora state introdotte in Europa. In seguito Bonacci si assicurò l’aiuto di suo figlio per portare avanti il commercio della repubblica pisana e lo mandò in viaggio in Egitto, Siria, Grecia, Sicilia e Provenza. Leonardo ,grazie a questi viaggi all’estero, potè studiare e imparare le tecniche matematiche impiegate in queste regioni. Intorno al 1200, Fibonacci tornò a Pisa dove per i 25 anni successivi lavorò alle sue personali composizioni matematiche. In tutta la sua produzione l’opera più importante è il "Liber abaci", comparso attorno al 1228: è un lavoro contenente quasi tutte le conoscenze aritmetiche e algebriche ed ha avuto una funzione fondamentale nello sviluppo della matematica dell’Europa occidentale. In particolare la numerazione indo-arabica, che prese il posto di quella latina semplificando notevolmente i commerci extraeuropei, fu conosciuta in Europa tramite questo libro. In tale sistema di numerazione, il valore delle cifre dipende dal posto che occupano: pertanto egli fu costretto ad introdurre un nuovo simbolo, corrispondente allo zero "0", per indicare le posizioni vacanti. La reputazione di Leonardo come matematico divenne così grande che l’imperatore Federico II gli chiese un’udienza mentre era Pisa nel 1225. Dopo il 1228 non si sa in sostanza niente della vita di Leonardo tranne il decreto della Repubblica di Pisa che gli conferì il titolo di "Discretus et sapiens magister Leonardo Bigollo" a riconoscimento dei grandi progressi che apportò alla matematica. Fibonacci morì qualche tempo dopo il 1240, presumibilmente a Pisa.

 

PRESENTAZIONE DELLA SERIE DI FIBONACCI

Il matematico pisano Leonardo Fibonacci fu ricordato soprattutto per via della sua sequenza divenuta ormai celeberrima. L’uso della sequenza di Fibonacci risale all’anno 1202. Essa si compone di una serie di numeri nella quale ognuno di essi è la somma dei due numeri precedenti (0,1,1,2,3,5,8,13,21…).Nella seconda metà del diciannovesimo secolo, un matematico francese di nome Edouard Lucas riprese lo studio di tale sequenza prendendo come valori di partenza 2 e 1. Questa versione dei numeri fu conosciuta come la sequenza di Lucas. Quest’ultimo fu colui che rese i numeri di Fibonacci noti a tutti. Johannes Kepler notò poi che facendo il rapporto fra due numeri di Fibonacci consecutivi, esso si avvicinava sempre più a 1,61803, valore noto anche con il nome di rapporto aureo.

 

APPLICAZIONE DEI NUMERI DI FIBONACCI ALLA MATEMATICA E AD ALTRE AREE

I numeri di Fibonacci hanno una innumerevole gamma di applicazione, soprattutto in matematica ma anche in altre aree, quali la biologia, l'architettura, l'economia e l'informatica. Ci concentreremo ora soprattutto sulla matematica, quindi sull'economia e sull'informatica.

LIBER ABACI

Uno dei più importanti libri di matematica del Medioevo è il Liber abbaci, scritto nel 1202 da Leonardo Pisano, meglio conosciuto come Fibonacci. Il Liber abbaci, più noto con il titolo di Liber abaci, è considerato un vero e proprio manuale di aritmetica e algebra con il quale, all’inizio del XIII secolo, Fibonacci ha introdotto in Europa il sistema numerico decimale indo-arabico e i principali metodi di calcolo ad esso relativi.
Il libro non tratta l’utilizzo dell’abaco e il suo titolo può essere tradotto in “Libro del calcolo”.
I primi capitoli del Liber abaci sono dedicati all’introduzione del sistema numerico decimale e delle principali operazioni di moltiplicazione, addizione, sottrazione e divisione, tra numeri interi e frazioni. A partire dall’ottavo capitolo sono invece presentati vari metodi algebrici per la risoluzione di problemi di matematica applicata, legati alla realtà dell’epoca, in particolare all’ambiente commerciale. Il dodicesimo e il tredicesimo capitolo sono legati al metodo di falsa posizione e al metodo di doppia falsa posizione. Il metodo di falsa posizione è un metodo per la risoluzione di problemi algebrici riconducibili ad equazioni o sistemi di equazioni lineari; il metodo di doppia falsa posizione, di origine araba, noto anche come metodo elchataym, consente di affrontare problemi riconducibili ad equazioni lineari della forma ax=b o della forma ax + b=c. A differenza del metodo di falsa posizione, nell’ elchataym sono scelte arbitrariamente due “false posizioni” da cui ricavare due approssimazioni distinte della condizione fissata, che la soluzione esatta deve fissare.La maggior parte delle procedure di calcolo introdotte da Fibonacci ha inoltre fondamento teorico nel metodo principale delle Proporzioni e negli altri algoritmi presentati negli “Elementi” di Euclide.
Gli Elementi di Euclide sono la più importante opera sulla matematica giuntaci dalla cultura greca antica. Composti tra il IV e III secolo a.C., rappresentano un quadro completo e definito dei principi della geometria noti al tempo. L’opera consiste in 13 libri: i primi 6 riguardanti la geometria piana, 3 sulla teoria dei numeri, il decimo libro sulla teoria degli incommensurabili e gli ultimi 3 sulla geometria solida.

 

LA SERIE DI FIBONACCI

Nel Liber Abaci (“Il Libro dell’Abaco”), in cui Fibonacci espone i fondamenti di algebra e matematica usati nei paesi Arabi, un problema fornisce l’occasione per l’introduzione della serie numerica che oggi porta il nome del matematico pisano: la serie di Fibonacci.

Intesa  come una successione di numeri interi definita dalla coppia 1,1 in cui l’elemento successivo è calcolato come somma degli ultimi due.
Proviamo a calcolare i primi numeri della serie iniziando dalla coppia 1,1:
1+1= 2
1+2=3                                        
2+3=5                                                      
3+5=8
5+8=13
8+13=21. e così via.

 

RISCONTRO DELLA SERIA DI FIBONACCI IN NATURA

 

Questa formula si riscontra in numerosi esempi in natura, e tra questi figura anche l’approssimazione del Rapporto Aureo.
Se per esempio vengono esaminati i semi dei girasoli o la corteccia esterna di alcuni frutti, quali l’ananas o la pigna, si può notare che presentano due ordini di spirali che si avvolgono le une in senso orario e le altre in senso antiorario a formare un’eccezionale struttura ad elica. La domanda che ci si può porre è, quante spirali ci sono? Il numero delle spirali che si avvolgono in senso orario è lo stesso di quelle che si avvolgono in senso antiorario?
Provando a calcolarle si può verificare che la pigna ha 5 spirali in un verso e 8 nell’altro, l’ananas ne ha 8 in un verso e 13 nell’altro, la margherita ne ha 21 e 34, il girasole 55 e 89. Scrivendo questi numeri in sequenza si ha:
5, 8, 13, 21, 34, 55, 89

 

IL PROBLEMA DEI CONIGLI

S’introduca quindi il cosiddetto “problema dei conigli” formulato per la prima volta da Fibonacci stesso nel 1202, problema che ispirò i matematici dei tempi successivi.
Supponiamo che una coppia di conigli adulti, un maschio e una femmina, siano chiusi in un recinto e che generino una coppia di altri conigli, un maschio e una femmina ogni mese; se i nuovi nati sono in grado di generare a loro volta una nuova coppia di conigli dopo due mesi e si riproducono anch’essi una volta al mese, quanti conigli ci saranno nel recinto dopo un anno, se nel frattempo nessuno dei conigli è morto?       

Discutendo la soluzione di questo problema si mostra che ciascun termine dopo i primi due è la somma dei due termini immediatamente precedenti. Si ottiene così una successione di numeri identica a quella trovata nel caso dei girasoli, della margherita, dell’ananas, ecc., che è appunto la successione dei numeri di Fibonacci.
Un discorso di questo tipo, anche se può sembrare apparentemente banale o poco interessante, riveste invece grande importanza in matematica perché è legato alla generazione di sequenze di numeri.

I NUMERI DI FIBONACCI NEL TRIANGOLO DI PASCAL (BINOMIO DI NEWTON)

Ci accingiamo a determinare una relazione fra i numeri di Fibonacci ed altri numeri, non meno notevoli, i cosiddetti coefficienti binomiali, determinando alcune delle leggi che mettono in relazione questi numeri fra loro. Disponiamo i coefficienti binomiali nel seguente schema triangolare, il cosiddetto triangolo di Pascal:

cioè

le linee oblique congiungenti i numeri di questo schema triangolare sono chiamate le diagonali ascendenti del triangolo di Pascal. Esempi di tali diagonali sono appunto le linee passanti per i numeri 1, 4, 3 e 1, 5, 6, 1. Notiamo che la somma dei numeri che si trovano su una data diagonale ascendente è un numero di Fibonacci. Infatti, le prime due diagonali ascendenti del triangolo di Pascal sono formate dal solo numero 1.

SOMMA DI NUMERI DI FIBONACCI

Consideriamo la serie di Fibonacci A, B, C, D, E, G...
Se si sommano due o più numeri consecutivi di tale serie, sempre a partire da A, e si aggiunge ulteriormente "1", si ottiene sempre un altro numero di Fibonacci che nella sequenza segue di due posti l'ultimo termine della somma
( A+B+C+1 = E )
Per esempio:
1+1+2+3+5+1 = 13

In questo caso si sono sommati i primi cinque numeri di Fibonacci, si è aggiunto uno e si è ottenuto il settimo numero della sequenza.
Inoltre se si prendono due numeri di Fibonacci consecutivi e se ne fa il quadrato, la somma fra i quadrati è un altro numero di Fibonacci che nella sequenza occupa il posto risultante dalla somma delle posizioni dei due termini di partenza.

I NUMERI DI FIBONACCI E LA BORSA DI MILANO

Un’applicazione moderna dei numeri di Fibonacci si può riscontrare presso la borsa azionistica di Milano. Prendendo spunto da Leonardo Fibonacci da Pisa, uno dei più grandi protagonisti della storia della matematica, Ralph Elson Elliot elaborò una precisa teoria di previsione dei mercati finanziari con la quale in tempi recenti sono stati anticipati i più grandi rialzi e i più grandi crolli di borsa. Usando le onde di Elliot ed i numeri di Fibonacci, il docente universitario G. Migliorino ha previsto con incredibile precisione il punto minimo del drammatico ribasso dell’estate ‘98.

 

I NUMERI DI FIBONACCI NEL PROCESSORE PENITUM

I numeri di Fibonacci sono utilizzati anche nel sistema informatico di molti computer. In particolare vi è un complesso meccanismo basato su tali numeri, detto "Fibonacci heap" che viene utilizzato nel processore Pentium della Intel per la risoluzione degli algoritmi.

 

EULERO

 

BIOGRAFIA

Eulero nacque a Basilea figlio di Paul Euler, un pastore protestante, e di Marguerite Brucker. Ebbe due sorelle di nome Anna Maria e Maria Magdalena. La famiglia si trasferì poi a Riehen, dove Eulero passò la maggior parte dell'infanzia. Paul Euler era amico della famiglia Bernoulli, e di Johann Bernoulli, uno dei più famosi matematici d'Europa. Eulero entrò all'università di Basilea tredicenne e si laureò in filosofia. A quel tempo riceveva anche lezioni di matematica da Johann Bernoulli, che aveva scoperto il suo enorme talento. Il padre di Eulero voleva che diventasse un teologo e gli faceva studiare il greco e l'ebraico. Fortunatamente Bernoulli convinse il padre di Eulero che egli era destinato alla carriera matematica. Nel 1726 Eulero completò il suo dottorato sulla propagazione del suono e, nel 1727, partecipò al Grand Prix dell'Accademia francese delle scienze. Il problema di quell'anno riguardava il miglior modo di disporre gli alberi su di una nave. Arrivò secondo subito dopo Pierre Bouguer ora riconosciuto come il padre dell'architettura navale. Eulero comunque vinse quel premio ben dodici volte nella sua vita.

 

In quegli anni i due figli di Johann Bernoulli, Daniel e Nicolas lavoravano all'Accademia Imperiale delle scienze di San Pietroburgo. Nel 1726, Nicolas morì e Daniel prese la cattedra di matematica e fisica del fratello, lasciando vacante la sua cattedra in medicina. Per questa fece quindi il nome di Eulero, che accettò. Eulero arrivò nella capitale russa nel 1727. Poco tempo dopo passò dal dipartimento di medicina a quello di matematica. In quegli anni alloggiò con Daniel Bernoulli con cui avviò un'intensa collaborazione matematica. Grazie alla sua incredibile memoria Eulero imparò facilmente il russo. L'Accademia più che un luogo d'insegnamento era un luogo di ricerca. Pietro il Grande infatti aveva creato l'Accademia per richiudere il divario scientifico tra la Russia e l'Occidente. Dopo la morte di Caterina I che aveva continuato la politica di Pietro venne al potere Pietro II. Questi, sospettoso degli scienziati stranieri, tagliò i fondi di Eulero e i suoi colleghi. Nel 1734, il matematico sposò Katharina Gsell, figlia di un pittore, e due si trasferirono in una casa vicino al fiume Neva.

 

I continui tumulti in Russia avevano stancato Eulero che amava una vita più tranquilla. Gli fu offerto un posto all'Accademia di Berlino da Federico il Grande di Prussia. Eulero accettò e partì per Berlino nel 1741. Visse a Berlino per i successivi 25 anni. In tale lasso di tempo pubblicò ben 380 articoli, oltre che alle sue due opere principali l' Introductio in analysin infinitorum, del 1748 e l'Institutiones calculi differentialis (1765). Scrisse oltre 200 lettere riguardanti le scienze che furono pubblicate in un libro che vendette moltissimo: Lettere a una principessa tedesca. Il libro, la cui popolarità testimonia una forte capacità divulgatrice del matematico, fornisce anche molte informazioni sulla sua personalità e sulle sue credenze religiose. Nonostante Eulero arrecasse un'enorme prestigio all'Accademia, dovette però allontanarsi da Berlino per un conflitto col Re. Egli infatti lo riteneva troppo poco raffinato per la sua corte, in cui alloggiava addirittura Voltaire. Eulero era infatti un religioso semplice e un gran lavoratore e aveva idee e gusti molto convenzionali. Era, in un certo senso, l'esatto opposto di Voltaire e questo lo rendeva bersaglio delle battute del filosofo.
In Russia la situazione politica si stabilizzò e Caterina la Grande, salita al potere e nel 1766, lo invitò a San Pietroburgo. Egli accettò e ritornò in Russia dove restò fino alla sua morte. Il suo soggiorno fu inizialmente funestato da un evento tragico: nel 1771, mentre lavorava nel suo studio per San Pietroburgo si propagò un incendio. Eulero, praticamente cieco, non se ne accorse fino a quando il suo ufficio non fu completamente avvolto dalle fiamme. Fu portato fortunosamente in salvo insieme a gran parte della sua biblioteca, ma tutti i suoi appunti andarono in fumo.
Nel 1773 perse la moglie, ancora quarantenne. Si risposò tre anni dopo. Il 18 settembre 1783, in una giornata come le altre, in cui discusse del nuovo pianeta Urano appena scoperto, scherzò col nipote e gli fece lezione, fu colto improvvisamente da un'emorragia cerebrale e morì poche ore dopo. Aveva 76 anni. Il suo elogio funebre fu scritto da Nikolaus von Fuss e dal filosofo e matematico Marquis de Condorcet.

 

NOTAZIONE MATEMATICA

Eulero introdusse moltissime notazioni in uso ancora oggi: tra queste, f(x) per la funzione, l'attuale notazione per le funzioni trigonometriche come seno e coseno, e la lettera greca Σ per la sommatoria. Per primo usò la lettera e per indicare la base dei logaritmi naturali, un numero reale che ora è appunto chiamato anche numero di Eulero, e la lettera i per indicare l'unità immaginaria. L'uso della lettera greca π per indicare pi greco, introdotto all'inizio del XVIII secolo da William Jones, diventò standard dopo l'utilizzo che ne fece Eulero.

ANALISI COMPLESSA

Euler diede importanti contributi all'analisi complessa. Scoprì quella che è oggi chiamata formula di Eulero:

Da questa ricavò l'identità di Eulero

Questa formula, ritenuta da Richard Feynman "la più bella formula di tutta la matematica", collega armoniosamente cinque numeri estremamente importanti: e, π, i, 1 e 0.

 

ANALISI

L'analisi era il campo di studio principale del XVIII secolo e i Bernoulli, amici di Eulero, erano i principali esperti del settore. Scopo principale di Eulero era catturare l'infinito, effettuare operazioni ancora non ben formalizzate, quali somme e prodotti di un numero infinito di numeri. Benché tali operazioni fossero al tempo mancanti di una solida base formale (data oggi dal concetto di limite di una successione e dalla struttura assiomatica dei numeri reali) e le sue dimostrazioni non fossero quindi completamente rigorose, portarono comunque a numerosi risultati corretti che fecero fare all'analisi un grosso passo in avanti.
Per prima cosa Eulero introdusse il concetto di funzione, l'uso della funzione esponenziale e dei logaritmi. Trovò i modi di esprimere le varie funzioni logaritmiche in termini di serie e definì i logaritmi per i numeri complessi e negativi, espandendone notevolmente la portata.
Eulero calcolò quindi il risultato di un certo numero di serie importanti, anche se, come è stato accennato, a quel tempo il significato di "somma e/o prodotto di infiniti termini" non era ancora rigorosamente formalizzato. Ad esempio,

Scoprì anche lo sviluppo dell'arcotangente

Nel 1735 risolse il Problema di Basilea

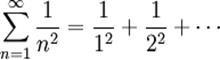
Successivamente trovò la forma chiusa per la somma dell'inverso di ogni potenza pari. Definì così in modo implicito la funzione zeta di Riemann. Studiando questa funzione scoprì in seguito il Prodotto di Eulero e suggerì per primo la formula di riflessione per la funzione zeta.
Inoltre Eulero introdusse la Funzione gamma e un nuovo metodo per risolvere l'equazione di quarto grado. Trovò un metodo per calcolare gli integrali usando i limiti complessi. Introdusse la costante di Eulero-Mascheroni definita come:

Eulero inoltre aprì la strada all'applicazione di metodi analitici nella teoria dei numeri: unì due rami disparati della matematica ed introdusse un nuovo campo dello studio, la teoria analitica dei numeri. Per esempio Eulero dimostrò l'infintità dei numeri primi partendo dalla divergenza della serie armonica.
Infine, Eulero contribuì enormemente alla nascita del calcolo delle variazioni con le equazioni di Eulero-Lagrange.

 

TEORIA DEI NUMERI

Il grande interesse di Eulero alla teoria dei numeri fu acceso dal suo amico Christian Goldbach. Molto del suo lavoro sulla teoria dei numeri riguarda la dimostrazione (o confutazione) delle molte congetture di Pierre de Fermat.
Eulero provò la correlazione tra numeri primi e funzione zeta di Riemann scoprendo la formula prodotto di Eulero. Provò poi le identità di Newton, il piccolo teorema di Fermat, il teorema di Fermat sulle somme di due quadrati e diede importanti contributi alla risoluzione del teorema dei quattro quadrati e alla comprensione dei numeri perfetti. Inventò la funzione phi di Eulero φ(n) che assegna a ogni numero naturale il numero di numeri minori di esso e coprimi ad esso. Con questa funzione generalizzò il piccolo teorema di Fermat (teorema di Eulero). Eulero congetturò inoltre la legge della reciprocità quadratica.
Uno dei più grandi successi di Eulero in questo campo fu però la dimostrazione dell'ultimo teorema di Fermat per il caso particolare in cui n=3, ossia la dimostrazione che la somma di due cubi non può essere uguale a un cubo. Questa dimostrazione è effettuata per discesa infinita e fa uso anche dei numeri complessi.

 

GEOMETRIA ANALITICA

Eulero diede anche importanti contributi alla geometria analitica come la formulazione delle equazioni che descrivono il cono, il cilindro, e le varie superfici di rotazione. Dimostrò anche che la geodetica passante per due punti in una qualsiasi superficie si trasforma nella retta passante per quei due punti se la superficie viene appiattita. Fu il primo a considerare tutte le curve insieme senza una predilezione per le coniche e a studiare a fondo anche le curve generate da funzioni trascendenti come la sinusoide.
Svolse anche un importante lavoro di classificazione delle curve e delle superfici. Nell'Introductio in analysin infinitorum si trova poi una completa ed esauriente trattazione delle coordinate polari che vengono esposte nella forma moderna. Per ciò, ancora oggi, spesso si indica erroneamente Eulero come l'inventore di questo sistema di notazione.
Dimostrò anche un paio di semplici teoremi di geometria pura, come per esempio l'affermazione che il circocentro, il baricentro e l'ortocentro di un triangolo sono sempre allineati. In suo onore tale retta fu chiamata retta di Eulero.

 

TEORIA MUSICALE

Fra i contributi meno noti di Eulero vi è anche un tentativo di formulare una teoria musicale su basi interamente matematiche. A questo è dedicato il suo trattato Tentamen novae theoriae musicae del 1739, e numerosi altri scritti. Questo lavoro si inserisce in un filone della ricerca matematica a cui avevano già contribuito Marin Mersenne e Cartesio, e che sarà successivamente ripreso da Jean d'Alembert, Hermann von Helmholtz e altri. Nel suo Elogio di Leonhard Euler (1783), il suo assistente Nikolaus Fuss definì quel trattato.

 

FISICA E ASTRONOMIA

Eulero contribuì a sviluppare l'equazione di fascio di Eulero-Bernoulli, una pietra miliare dell'ingegneria. Eulero non solo risolse con successo molti problemi fisici ma, ebbe l'idea di applicare le stesse tecniche alla meccanica celeste. Realizzò vari lavori astronomici quali la determinazione esatta delle orbite delle comete e di altri corpi celesti, ed il calcolo della parallasse del Sole.

 

OPERE

• Mechanica, sive motus scientia analytica exposita 
• Tentamen novae theoriae musicae 
• Solutio problematis ad geometriam situs pertinentis 
• Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti 
• Introductio in analysin infinitorum 
• Institutiones calculi differentialis 
• Theoria motus corporum solidorum seu rigidorum 
• Institutiones calculi integralis 
• Vollständige Anleitung zur Algebra
• Lettres à une Princesse d'Allemagne 

 

 

CONGETTURA DI GOLDBACH

In matematica, la congettura di Goldbach è uno dei più vecchi problemi irrisolti nella teoria dei numeri. Esso afferma:
Ogni numero pari maggiore di 2 può essere scritto come somma di due numeri primi. (Lo stesso numero primo può essere usato due volte)
Per esempio,
  4 = 2 + 2
  6 = 3 + 3
  8 = 3 + 5
10 = 3 + 7 = 5 + 5
12 = 5 + 7
14 = 3 + 11 = 7 + 7
etc.

ORIGINI

Nel 1742, il matematico prussiano Christian Goldbach scrisse una lettera a Leonhard Eulero in cui propose la seguente congettura:
Ogni numero dispari maggiore di 5 può essere scritto come somma di tre numeri primi.
Eulero, interessandosi al problema, rispose con una versione più forte della congettura:
Ogni numero pari maggiore di 2 può essere scritto come somma di due numeri primi.
La prima delle due è oggi conosciuta come congettura "debole" di Goldbach, la seconda come congettura "forte" di Goldbach. (L'enunciato della versione forte implica quello della congettura debole, poiché ogni numero dispari > 1 può essere ottenuto aggiungendo 3 ad ogni numero pari compreso lo 0). Si conviene che il termine congettura di Goldbach sia sinonimo di congettura forte di Goldbach. Entrambi i problemi sono rimasti irrisolti fino ad oggi.

 

RISULTATI

La congettura di Goldbach è stata attaccata da molti teorici dei numeri. La maggior parte dei matematici ritiene che la congettura sia vera, basandosi principalmente su considerazioni statistiche e probabilistiche ottenute con il teorema dei numeri primi: più grande è il numero pari, più diventa probabile che possa essere scritto come somma di due primi.
Intorno al 1930 furono compiuti alcuni progressi. Dapprima, nel 1937, Ivan Vinogradov dimostrò che ogni numero pari è somma di tre primi, e che quasi tutti i numeri pari possono essere scritti come somma di due primi. In particolare, l'insieme dei numeri che non soddisfano le ipotesi di Vinogradov ha densità 0.
Nel 1938, T. Estermann mostrò che quasi tutti i numeri pari possono essere scritti come somma di due primi, e N. Pipping verificò laboriosamente la congettura per tutti gli n ≤ 10 000. Successivamente L.G. Schnirelmann provò nel 1939 che ogni numero pari n ≥ 4 può essere scritto come somma di al più 300 000 numeri primi. Questo numero è stato successivamente abbassato da numerosi ricercatori. Il risultato più forte attualmente disponibile, dimostrato da Olivier Ramaré nel 1995, è che ogni numero pari n ≥ 4 si può scrivere come somma di al più 6 numeri primi.
I matematici successivi hanno sviluppato altri approcci. Un metodo tenta di dimostrare che "ogni numero pari maggiore di 4 può essere scritto come somma di c primi". Un'ulteriore generalizzazione sulle stesse linee sarebbe quella di dimostrare che "ogni multiplo di c maggiore di c stesso può essere scritto come somma di c primi". In entrambe le formulazioni, la congettura di Goldbach è il caso speciale dove c = 2. Un altro metodo tenta di dimostrare che "ogni numero pari può essere scritto come somma di un numero i cui fattori primi sono in numero non superiore ad a e un numero i cui fattori primi sono in numero non superiore a b". Questa è chiamata "proposizione (a+b)". In questo approccio, la congettura di Goldbach è il caso speciale dove a = 1 e b = 1; cioè, quando entrambi i numeri sono primi. Quella di Goldbach sarebbe insomma la "proposizione (1+1)".
Chen Jingrun mostrò nel 1966 che ogni numero pari abbastanza grande può essere scritto come somma o di due primi, o di un primo ed un semiprimo.
H.A. Pogorzelski diffuse una dimostrazione della congettura nel 1977, che però non è generalmente accettata nella comunità matematica.
T. Oliveira e Silva gestisce un progetto di calcolo distribuito che ha finora verificato la congettura fino a 6 × 1017 (aggiornato a febbraio 2007).

 

CURIOSITA’

• Il Matematico Automatico di Doug Lenat riscoprì la congettura di Goldbach nel 1982. Questa è considerata una delle prime constatazioni del fatto che gli strumenti della intelligenze artificiali sono capaci di compiere scoperte scientifiche.

Nel 2000, allo scopo di pubblicizzare il libro Lo zio Petros e la congettura di Goldbach di Apostolos Doxiadis, l'editore britannico Tony Faber offrì un premio di 1 000 000 di dollari per una dimostrazione della congettura. Il premio sarebbe stato assegnato solo per dimostrazioni inviate per la pubblicazione entro aprile 2002, ma mai reclamato.

 

LUCA PACIOLI

 

BIOGRAFIA

Fra Luca Pacioli o Luca di Borgo nacque a Borgo San Sepolcro nel 1445 e lì visse fino al 1464.
Fu un insigne matematico ed umanista al pari di Piero della Francesca (di cui fu allievo) e di Leonardo da Vinci, con i quali approfondì degli studi che gli consentirono la stesura della “Summa de arithmetica, geometria, proportioni et proportionalità”; studi che gli valsero l’appellativo di “ragioniere di Leonardo”.
Studiò matematica a Venezia alla scuola di Rialto, sotto la guida di Domenico Bragadin.
Viaggiò  a   lungo  per  Antonio  Rompiasi  per  i cui
figli,   nel  1470,   compose    un   primo   trattato  di
matematica.
Nel 1477 entrò nell’ordine dei frati minori francescani e si dedicò allo studio della teologia e della filosofia.
Insegnò a Perugia, Venezia, Firenze, Milano, Pisa, Bologna e Roma ove si crede morì nel 1517.
Uno dei periodi più significativi della vita di fra Luca fu quello compreso tra il 1494 ed il 1499.
Nel 1494 infatti Ludovico il Moro gli conferì la cattedra di matematica  a Milano, dove strinse amicizia con Leonardo da Vinci. Nello stesso annno pubblicò a Venezia la “Summa”.
Sotto l’influenza di Leon Battista Alberti, Piero della Francesca e Leonardo da Vinci compose, nel 1496, la “Divina proportione”, pubblicata poi nel 1509.
L’opera del Pacioli costituisce il coronamento e la sintesi della matematica del Medioevo e proprio in questo sta la sua importanza.

Nel 1994 la Zecca dello Stato Italiano coniò una moneta da 500 lire in onore di Luca Pacioli.

 

 

LE OPERE

Le principali opere di Luca Pacioli sono due: la “Summa de arithmetica, geometria, proportioni et proportionalità”, e la “Divina proporzione”.

La prima venne pubblicata a Venezia nel 1494 ed è una vera e propria “enciclopedia matematica”. Scritta in volgare, come egli stesso dichiara (in realtà utilizza un miscuglio di termini latini, italiani e greci), contiene un trattato generale di aritmetica e di algebra, elementi di aritmetica utilizzata dai mercanti (con riferimento alle monete, pesi e misure utilizzate nei diversi stati italiani). Uno dei capitoli della Summa è intitolato Tractatus de computis et scripturis; in esso viene presentato per la prima volta il concetto di partita doppia (e quindi: dare e avere, bilancio, inventario) che poi si diffuse per tutta Europa col nome di “metodo veneziano”, perché usato dai mercanti di Venezia. Il Pacioli scrive:

“Mai si deve mettere in dare
che quella ancora non si ponga in avere,
e così mai si deve mettere cosa in avere
che quella medesima con suo ammontare non si metta in dare.
E di qua nasci poi al bilancio che del libro si fa:
nel suo saldo tanto convien che sia il dare quanto l’avere”

 

 

Il “De Divina proporzione” venne invece composto nel 1497 ma pubblicato poi successivamente nel 1509, con le celebri incisioni dovute a Leonardo da Vinci raffiguranti suggestive figure poliedriche.
Sono le questioni attinenti al rapporto aureo che danno il titolo al libro, che si estende poi a questioni cosmologiche e matematiche; ed ancora a temi di architettura (presi in prestito da Vitruvio e da Leon Battista Alberti), a questioni relative alla prospettiva (campo in cui attinge molto dall’opera del suo cittadino Piero della Francesca) ed altro ancora.

 

 

GIROLAMO CARDANO

BIOGRAFIA

Gerolamo Cardano nasce a Pavia il 24 settembre 1501. Il padre Fazio, insegnava alle Scuole Piatti, ed è citato da Leonardo da Vinci nel Codice Atlantico (f.225) a proposito di un libro di matematica. La madre di Gerolamo, Clara Micheria, non era sposata con Fazio per cui, quando era rimasta incinta, per nascondere la gravidanza aveva dovuto trasferirsi a Pavia .Gerolamo nasce dunque a Pavia; ma subito dopo la nascita, per sfuggire alla peste che imperversava, viene portato a Moirago dove resta per 3 anni, finché viene portato a Milano dove vive con la madre e la zia Margherita; in seguito la famiglia si riunisce e si trasferisce in un’altra zona di Milano.
Fin da bambino Gerolamo si dimostra dotato di grande spirito di osservazione e di una fervida immaginazione. I genitori occupano della sua istruzione  insegnandogli a leggere,scrivere, la matematica e la musica.

MATEMATICA

Oggi egli è noto soprattutto per i suoi contributi all'algebra. Ha pubblicato le soluzioni dell'equazione cubica e dell'equazione quartica nella sua maggiore opera matematica, intitolata Ars magna stampata nel 1545. Parte della soluzione dell'equazione cubica gli era stata comunicata da Tartaglia che successivamente aveva sostenuto che Cardano aveva giurato di non renderla pubblica, e aveva così avviato una disputa durata un decennio. Cardano pubblicò il suo testo quando venne a sapere che il Tartaglia aveva a sua volta ricevuto la soluzione dal bolognese Scipione Dal Ferro. L'equazione quartica è risolta da Lodovico Ferrari, uno studente di Cardano. Nella prefazione dell'Ars Magna vengono accreditati sia Tartaglia che Ferrari. Nei suoi sviluppi delle soluzioni Cardano occasionalmente si serve dei numeri complessi, ma senza riconoscerne l'importanza come invece saprà fare Rafael Bombelli.

 

NIELS HENRIK ABEL

BIOGRAFIA

Matematico norvegese noto soprattutto per i suoi studi sull’algebra e sulla teoria delle funzioni, nel 1815 entrò alla scuola Cattedrale di Cristiania (oggi Oslo) e qui tre anni più tardi diede prova del suo genio matematico con le sue brillanti soluzioni agli originali problemi proposti da Bernt Holmboe.
Ma il primo rilevante lavoro di Abel riguardò la dimostrazione dell’impossibilità di risolvere le equazioni di quinto grado tramite radicali: questa, nel 1824, fu la sua prima ricerca ad essere pubblicata ma la dimostrazione era difficile e astrusa. Successivamente fu pubblicata in forma più elaborata nel primo volume del Giornale di Crelle.
Abel fece anche una brillante ricerca nella teoria delle funzioni, studiando soprattutto le ellittiche e le iperellittiche, ed introducendo una nuova classe di funzioni oggi note come funzioni abeliane, oggetto di suo approfondito studio particolare.
Nel 1826 Abel andò a Parigi dove rimase una decina di mesi; qui conobbe i più grandi matematici francesi, ma lui ed il suo lavoro furono poco apprezzati, anche a causa della sua modestia che non lo spinse a proclamare i risultati dei suoi studi.
Le difficoltà finanziarie costrinsero Abel ad interrompere il suo viaggio per tornare in Norvegia; all’inizio dell’aprile del 1829 Crelle lo aiutò ad ottenere un incarico a Berlino, ma l’offerta raggiunse la Norvegia dopo due giorni dalla sua morte, causata dalla polmonite.

CONTRIBUTI  MATEMATICI

La dimostrazione che Abel diede della irresoluzione delle equazioni di quinto grado tramite radicali, è un teorema che non asserisce che le equazioni di grado superiore al quarto siano insolubili; infatti, tutte le equazioni polinomiali hanno soluzione ( perlomeno nel campo dei numeri complessi), come afferma il teorema fondamentale dell’algebra. Nonostante tali soluzioni non possano essere espresse algebricamente in maniera esatta, esse possono essere calcolate fino ad un grado di precisione arbitrario usando tecniche numeriche come il metodo di Newton-Raphson o il metodo di La guerre, e in questo modo non sono diverse dalle soluzioni delle equazioni polinomiali di secondo, terzo e quarto grado. Il teorema riguarda solo la forma che una soluzione deve avere: la soluzione di un’equazione di grado superiore al quarto non può essere espressa partendo dai coefficienti utilizzando soltanto le operazioni di addizione, sottrazione, moltiplicazione, divisione ed estrazione di radice.
Per esempio, le soluzioni di qualunque equazione polinomiale di secondo grado possono essere espresse con la semplice formula :

Formule analoghe per equazioni di terzo e quarto grado, utilizzando radici cubiche e radici quarte, sono note solo dal sedicesimo secolo.

La morte prematura di questo talento matematico mise fine ad una brillante e promettente carriera. Le sue indagini hanno chiarito delle maggiori oscurità dell’analisi ed hanno aperto nuovi campi di studio, permettendo numerose ramificazioni alla conoscenza matematica e consentendo notevoli progressi. La parte più profonda ed originale del lavoro di Abel fu pubblicata sul Giornale di Crelle di cui era editore Holmboe. Un’edizione più completa dei suoi lavori fu pubblicata nel 1882 da Ludwig Sylow e Sophius Lie. L’aggettivo abeliano, divenuto comune negli scritti matematici, deriva dal suo nome e convenzionalmente è indicato con una maiuscola.
Nel 2002 fu anche istituito in suo onore il prestigioso premio Abel.

 

ULTIMO TEOREMA DI FERMAT

 

Il famoso teorema, per n > 2 non ha soluzione nei numeri interi.
L'ultimo Teorema di Fermat afferma che non esistono soluzioni intere positive all'equazione:

se n > 2.

           Quest’'ipotesi fu formulata da Pierre de Fermat nel 1637. Egli non fornì però una dimostrazione, che fu cercata invano nei secoli a venire.

 

Fermat scrisse, a proposito di essa, ai margini di una copia dell'Arithmetica di Diofanto, sulla quale era solito formulare molte delle sue famose teorie:
"Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina".
La dimostrazione del "Teorema di Fermat" fu cercata tra gli altri da:

• Eulero, che, nel XVII secolo, formulò una dimostrazione valida solo per n=3;

• Adrien-Marie Legendre, che risolse il caso n=5;

• Sophie Germain, che, lavorando sul teorema, scoprì che esso era probabilmente vero per n uguale ad un particolare numero primo p, tale che 2p + 1 è anch'esso primo: i primi di Sophie Germain.

Solo nel 1994, dopo 7 anni di dedizione completa al problema, e dopo un falso allarme nel 1993, Andrew Wiles, affascinato dal teorema che da bambino sognava di risolvere, riuscì a dare finalmente una dimostrazione. Utilizzò tuttavia elementi di matematica ed algebra moderna che Fermat non poteva conoscere; di conseguenza, il teorema può essere riferito anche con il nome di teorema di Fermat - Wiles.
È chiaro quindi come la soluzione di Wiles (pubblicata nel 1995 e premiata due anni dopo, il 27 giugno 1997 con il Premio Wolfskehl consistente in una borsa di 50.000 dollari) non sia la stessa che Fermat affermava di aver trovato; quasi tutti i matematici sono dell'idea che Fermat si fosse sbagliato e non possedesse una dimostrazione corretta.

 

IL CONTESTO MATAMATICO

L'ultimo teorema di Fermat è una generalizzazione dell'equazione diofantea a2 + b2 = c2. Già antichi Greci e Babilonesi sapevano che questa equazione ha delle soluzioni intere, come (3, 4, 5) (32 + 42 = 52) o (5, 12, 13). Queste soluzioni sono conosciute come terne pitagoriche e ne esistono infinite, anche escludendo le soluzioni banali per cui a, b e c hanno un divisore in comune e quelle ancor più banali in cui almeno uno dei numeri è uguale a zero.
Secondo l'ultimo teorema di Fermat, non esistono soluzioni intere positive quando l'esponente 2 è sostituito da un numero intero maggiore. Mentre il teorema stesso non si presta a nessuna applicazione, cioè non è stato usato per dimostrare altri teoremi, è particolarmente noto per la sua correlazione con molti argomenti matematici che apparentemente non hanno nulla a che vedere con la teoria dei numeri, e per questo motivo non è soltanto una curiosità matematica di poca importanza. Inoltre, la ricerca di una dimostrazione è stata all'origine dello sviluppo di importanti aree della matematica.

 

LE ORIGINI

Il teorema deve essere dimostrato soltanto per n=4 e nel caso in cui n è un numero primo: se infatti si trovasse una soluzione akp + bkp = ckp, si avrebbe immediatamente una soluzione (ak)p + (bk)p = (ck)p.
Fermat stesso ha dimostrato in un altro suo lavoro il caso n=4, anzi il risultato più forte che non esiste una terna (a, b, c) tale che a4 + b4 = c2 (ovviamente, se non esiste un c elevato al quadrato, non può nemmeno essercene uno elevato alla quarta potenza). Nel corso degli anni il teorema venne dimostrato per un numero sempre maggiore di esponenti speciali n, ma il caso generale rimaneva irrisolto.
Eulero dimostrò il teorema per n=3, Dirichlet e Legendre fecero lo stesso per n=5 nel 1825, Gabriel Lamé dimostrò il caso n=7 nel 1839.
Nel 1983 Gerd Faltings dimostrò la congettura di Mordell, che implica che per ogni n > 2, c'è al massimo un numero finito di interi coprimi a, b e c con an + bn = cn.

 

LA DIMOSTRAZIONE

Utilizzando sofisticati strumenti della geometria algebrica (in particolare curve ellittiche e forme modulari), della teoria di Galois e dell'algebra di Hecke, Andrew Wiles, dell'università di Princeton, con l'aiuto del suo primo studente Richard Taylor, diede una dimostrazione dell'ultimo teorema di Fermat che è stata pubblicata nel 1995 sulla rivista Annals of mathematics. Nel 1986, Ken Ribet aveva dimostrato la congettura epsilon di Gerhard Frey secondo la quale ogni contro-esempio an + bn = cn all'ultimo teorema di Fermat avrebbe prodotto una curva ellittica definita come:

che fornirebbe un contro-esempio alla congettura di Taniyama - Shimura.
Quest'ultima congettura propone un collegamento profondo fra le curve ellittiche e le forme modulari. Wiles e Taylor potevano stabilire un caso speciale della congettura di Taniyama-Shimura sufficiente per escludere tali contro-esempi in seguito all'ultimo teorema di Fermat. La storia della dimostrazione è così notevole quanto il mistero del teorema in sé. Wiles trascorre sette anni per risolvere quasi tutti i particolari da solo e con la massima segretezza (tranne una fase finale di revisione per cui si è avvalso dell'aiuto del suo collega di Princeton, Nick Katz). Quando ha annunciato la dimostrazione nel corso di tre conferenze tenute all'università di Cambridge tra il 21-23 giugno 1993, ha stupito il pubblico per il numero di idee e di costruzioni usate nella dimostrazione. Purtroppo, dopo un controllo più ravvicinato è stato scoperto un serio errore che ha sembrato condurre alla ripartizione di questa dimostrazione originale. Wiles e Taylor allora hanno trascorso circa un anno per far rivivere la dimostrazione e nel settembre 1994, hanno dato la dimostrazione finale e corretta utilizzando alcune tecniche differenti che Wiles aveva scartato nei suoi primi tentativi.
Tuttavia, gli strumenti matematici utilizzati non erano conosciuti ai tempi di Fermat, quindi sussiste il mistero sulla dimostrazione che questi ne avrebbe fornito.

 

 

FERMAT HA DATO REALMENTE UNA DIMOSTRAZIONE?

La citazione in latino diceva:
"Cubum autem in duos cubos, aut quadratoquadratorum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos euisdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet"
"È impossibile separare un cubo in due cubi, o una potenza quarta in due potenze quarte, o in generale, tutte le potenze maggiori di due come somma della stessa potenza. Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina"
Ci sono seri dubbi riguardo la rivendicazione di Fermat di aver trovato una dimostrazione veramente importante, che fosse corretta.
La lunghezza della dimostrazione di Andrew Wiles è circa 200 pagine ed è oltre la comprensione della maggior parte dei matematici di oggi. Spesso le dimostrazioni iniziali della maggior parte dei risultati non sono tipicamente le più dirette, è quindi possibile che ci sia una dimostrazione più corta e più elementare. Non è però verosimile che la dimostrazione di Wiles possa essere semplificata fino ad essere esprimibile con gli strumenti matematici posseduti da Fermat.
I metodi utilizzati da Wiles erano difatti sconosciuti quando Fermat scriveva e pare estremamente improbabile che Fermat sia riuscito a derivare tutta la matematica necessaria per dimostrare una soluzione. Andrew Wiles stesso ha affermato "è impossibile; questa è una dimostrazione del XX secolo".
Dunque, o esiste una dimostrazione più semplice che tutti gli altri matematici finora non hanno trovato, o, più probabilmente, Fermat semplicemente si sbagliò. Per questo sono particolarmente interessanti alcune dimostrazioni errate, ma ad una prima analisi plausibili, e che fossero alla portata di Fermat. La più nota si basa sul presupposto erroneo che l'unicità della scomposizione in fattori primi funzioni in tutti gli anelli degli elementi integrali dei campi sui numeri algebrici.
Questa è una spiegazione accettabile per molti esperti della teoria dei numeri, considerando che molti maggiori matematici successivi che hanno lavorato sul problema hanno seguito questo percorso e talvolta hanno anche creduto di aver dimostrato il teorema.
Il fatto che Fermat non abbia pubblicato, né comunicato a qualche amico o collega, nemmeno un abbozzo della dimostrazione può essere un indizio di un suo successivo ripensamento dovuto ad una tardiva scoperta di un errore nel suo tentativo di dimostrazione. Fermat, inoltre, pubblicò successivamente una dimostrazione per il caso speciale n=4 (ovvero a4 + b4 = c4). Se realmente avesse ritenuto di possedere una dimostrazione per il teorema generale, forse avrebbe preferito pubblicare quest'ultima e non il caso particolare.

 

 

CARTESIO

 

BIOGRAFIA

Renè Descartes è stato un filosofo e matematico francese, che diede fondamentali contributi a questi due campi del sapere.
E’ conosciuto anche con il nome di Renatus Cartesius , in Italia modificato Cartesio.
In giovane età fu educato dai gesuiti nel collegio di La Flèche, dove approfondì, oltre ai classici, lo studio della matematica  e della filosofia scolastica.
In seguito studiò diritto presso l’università di Poitiers e dal 1618 si arruolò nell’esercito deciso a intraprendere una carriera militare; la sua attenzione era tuttavia già rivolta ai problemi filosofici e matematici ai quali avrebbe dedicato la vita.
Tra il 1623 e il 1625 viaggiò molto e poi si trasferì in Olanda dove compose tre importanti trattati: La Dottrica, Le Meteore e La Geometria, pubblicati nel 1637 e introdotti dal Discorso sul Metodo, che comprendeva la sua filosofia.
Nel 1650 Cartesio, ammalatosi di polmonite, morì.

CONTRIBUTI MATEMATICI

Cartesio contribuì notevolmente alle ricerche matematiche elaborando le basi concettuali della geometria analitica; inoltre, fu il primo matematico che cercò di classificare le curve secondo il tipo di equazione a esse associato, contribuendo così alla teoria delle equazioni.
Introdusse l’uso delle ultime lettere dell’alfabeto per designare le incognite e delle prime lettere dell’alfabeto per designare i termini noti. Inventò anche il metodo degli indici (come x2) per esprimere le potenze dei numeri, Inoltre formulò la regola, nota come regola cartesiana dei segni, per trovare il numero delle radici positive e negative di qualsiasi equazione algebrica.
Cartesio  iniziò ad usare un sistema di coordinate che noi chiameremo oblique, quindi non sempre ortogonali, e solo con ascisse e ordinate positive, per cui tracciava solo le porzioni delle curve che giacevano nel primo quadrante.
Trasformò problemi geometrici in intersezioni di curve quali rette, coniche e altre ancora, ma non risolse problemi di intersezioni col calcolo algebrico, bensì mediante la costruzione geometrica delle curve.
Inoltre classificò le curve in base al grado di equazione, cioè modificò la classificazione dei greci in piane, solidi e lineari ( piane sono retta e circonferenza, solide le sezioni coniche, lineari tutte le altre quali la spirale, la cicloide..).

 

Fonte: http://share.dschola.it/helpmat/lcsella/Relazioni/IL%20TEOREMA%20DEL%20PAPPAGALLO.doc

Sito web da visitare: http://share.dschola.it

Autore del testo: Acquadro Elisa Cerruti M., Flem M.,Gallo M., Mella M., Quintavalle M., Rey L.

 

Nota : se siete l'autore del testo sopra indicato inviateci un e-mail con i vostri dati , dopo le opportune verifiche inseriremo i vostri dati o in base alla vostra eventuale richiesta rimuoveremo il testo.

Parola chiave google : Matemateci famosi biografie e teoremi tipo file : doc

 

Matemateci famosi biografie e teoremi

 

 

 

 

Visita la nostra pagina principale

 

Matemateci famosi biografie e teoremi

 

Termini d' uso e privacy