Equazioni e disequazioni

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Equazioni e disequazioni

Equazioni

Un’equazione è una relazione di uguaglianza tra due espressioni matematiche (membri) dove sono presenti delle variabili incognite. Risolvere un’equazione vuol dire individuare il valore dell’incognita per il quale la relazione è soddisfatta.

Il grado di un’equazione è pari al massimo esponente per il quale compare l’incognita. Le soluzione dell’equazioni sono tante quanto è il grado dell’equazione.

Equazioni di primo grado: le incognite compaiono ad esponente 1

ax+b=0

x = - b/a

La soluzione di un equazione di primo grado si trova dapprima isolando i termini con incognita dai termini noti. Un termine può cambiare di membro cambiando di segno.

2x + 5 = - 3x +10

2x + 3x = +10 - 5

5x = 5

Un termine può essere trasportato dal numeratore di un membro al denominatore dell’altro quando entrambi i membri sono ridotti ad uno stesso denominatore

x = 5 / 5 = 1

Equazioni di secondo grado: le incognite compaiono ad esponente 2

Una volta ridotta un’equazione di secondo grado assume al forma:

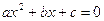
In generale le soluzioni di un equazione di 2° grado sono date da:

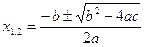
Quando l’espressione all’interno del radicale è negativa si parla di soluzioni di tipo immaginario e si fa ricorso al simbolo i che equivale alla

Disequazioni

Una disequazione è una relazione tra due espressioni matematiche (membri) dove sono presenti delle variabili incognite e dove compare al posto del segno = uno dei segni:

> maggiore (o maggiore stretto)

< minore (o minore stretto)

>= maggiore o uguale

<= minore o uguale

Anche le disequazioni hanno un grado e rimangono valide le regole di soluzione delle equazioni.

In questo caso il risultato non è un solo valore ma un intervallo di valori.

3x + 2 > 8

3x > 8-2

3x > 6

x > 6 / 3

x > 2

Il risultato significa che qualsiasi valore di x maggiore di 2 soddisfa la disequazione.

Nelle disequazioni se si cambia di segno ai due membri occorre invertire il verso della disequazione.

- x + 2 > - 8

x – 2 < 8

Nelle disequazioni di secondo grado occorre prestare attenzione al segno della disequazione. A partire da un termine di secondo grado positivo (nel caso non lo fosse si cambia segno a tutti i termini e si inverte il segno della disequazione) si osserva il segno della disequazione:

a>0 e segno maggiore (>0) allora i valori che soddisfano la disequazioni sono esterni alle due soluzioni:

a>0 e segno maggiore (<0) allora i valori che soddisfano la disequazioni sono esterni alle due soluzioni:

Fonte: http://nuke.cat-arezzo.org/Portals/0/MatematicaDispense.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : Equazioni e disequazioni tipo file : doc

Equazioni e disequazioni