Matematica finanziaria

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Matematica finanziaria

SCHEDE DI MATEMATICA FINANZIARIA 1

Introduzione

Matematica finanziaria: la matematica applicata agli scambi di denaro che capitano in momenti lontani nel tempo.

Le stesse formule si possono applicare anche ad altri fenomeni, come si mostrerà con qualche esempio in seguito.

Gli scambi di denaro lontani nel tempo non sono confrontabili direttamente; un esempio: se avrò un certo capitale fra 3 anni invece che oggi, dovrò rinunciare a tutto quello che potrei fare con quel capitale in questi 3 anni (come minimo, tenerlo in banca a maturare interessi; come massimo, spenderlo per comprarmi il necessario a non morire di fame) e ciò conta parecchio.

Se avere denaro ora è diverso (meglio) che avere denaro nel futuro, il denaro di oggi e quello di domani sono confrontabili non direttamente, ma soltanto dopo che si è definito quanto sia il vantaggio di averlo oggi.

Nella matematica finanziaria svolta in queste lezioni, si stabilisce che il vantaggio di avere denaro presto sia sempre quantificabile e che si identifichi con gli interessi.

Calcolo degli interessi in economia aziendale

Le formule usate in economia aziendale per il calcolo degli interessi sono della forma

(so che di solito per il tempo si usa il simbolo t e non s, ma qui il simbolo t verrà usato in un significato più adeguato ai calcoli successivi, come si capisce più avanti).

Al solito, I indica il valore degli interessi, C quello del capitale e r è il tasso d’interesse in percentuale a cui è stato tolto il simbolo %, mentre g vale 1 se s si calcola in anni, 12 se s si calcola in mesi, 365 se s si calcola in giorni e così via.

Numeri percentuali e numeri unitari

Fra i numeri percentuali p% e quelli unitari u (cioè i normali numeri in forma decimale), il legame è u = p/100, o anche p = 100´u.

Esempi:

se p% è 2%, allora u è 0,02;

se u è 0,34, allora p% è 34%.

Sono particolarmente significativi questi casi:

p% = 100% equivale a u = 1 e viceversa;

p% = 50% equivale a u = 0,5 e viceversa.

Quindi: invece del vecchio r%/100 di economia aziendale, useremo il nuovo r di matematica finanziaria.

Conteggio del tempo

Quando si misura il tempo, è essenziale chiarire quale sia l’unità di misura: giorni, settimane, mesi, trimestri, quadrimestri, semestri, anni, decenni o altro?

Esempi:

* se il periodo in cui misuro il tempo è l’anno, quando ho 8 mesi ho 8 dodicesimi (non DECIMI!) di anno, cioè 8/12 = 2/3 = 0,666... = 66,67% di anno; perciò 8 mesi sono i 2/3 di un anno, o anche il 66,67% di un anno;

* quando ho 615 giorni ho 615/365 = 1,6849 = 168,49% di anno, perciò 615 giorni sono i 615/365 = 123/73 di un anno, o anche il 168,49% di un anno.

Indicare una durata con un numero puro, come 5,3, non basta: bisogna specificare se quel 5,3 indica anni, mesi, secoli...

Se ho una durata s in una certa misura, ad esempio in mesi, e la voglio esprimere in un’altra misura, ad esempio in trimestri, devo dividere s per il numero di mesi che stanno in un trimestre: durata in trimestri = durata mesi/3. Infatti un mese è un terzo di trimestre...

Per stabilire con chiarezza la regola generale, conviene introdurre il concetto di frequenza: la frequenza di un periodo è il numero di periodi che servono per fare un anno. Ecco una scheda utile per fissare le idee.

La frequenza di un giorno è 360 nell’anno commerciale e 365 nell’anno civile.

La frequenza di una settimana è convenzionalmente fissata in 52.

La frequenza di un mese è 12.

La frequenza di un bimestre è 6.

La frequenza di un trimestre è 4.

La frequenza di un quadrimestre è 3.

La frequenza di un semestre è 2.

La frequenza di un anno è 1.

La frequenza di un biennio è 0,5.

La frequenza di un lustro (o quinquennio) è 0,2.

La frequenza di un decennio è 0,1.

In generale, se ho una durata s misurata in periodi di frequenza g e voglio trovare la durata equivalente t misurata in periodi di frequenza f, la regola è t = s/(g/f). Naturalmente, questa regola nasce dalla proporzione t : f = s : g.

Esempio: ho una durata s di 5 quadrimestri (perciò è g = 3) e voglio trovare l’equivalente durata t in semestri (perciò è f = 2).

Dato che è g/f = 1,5 (serve un quadrimestre e mezzo per fare un semestre), la durata cercata sarà t = 5/1,5 = 3,333...

Esempio più ricco: quanti anni si ottengono, con l’anno civile, sommando 3 anni e mezzo, due quadrimestri e 18 giorni?

Tre anni e mezzo sono 3,5 anni; due quadrimestri sono 2/3 = 0,666... di anno; 18 giorni con l’anno civile sono 18/365 = 0,049315 di anno; in totale, la durata in anni è 3,5+0,666...+0,049315 = 4,215982.

Esempio ulteriore: in mesi, quanto vale il risultato precedente?

Sarà 4,215982´12 = 50,59178 mesi.

Legame con il calcolo degli interessi come trattato in matematica finanziaria

In matematica finanziaria, la formula degli interessi viene scritta in modo un po’ diverso da quello usato in economia aziendale; i passaggi sono questi: . In altri termini, gli interessi si ottengono moltiplicando il capitale C per il tasso d’interesse r/100, quindi già in forma unitaria, e per la misura del tempo in anni s/g.

Questa misura è coerente con la regola mostrata sopra: dato che si sta cercando la misura in anni, si applicherà la formula t = s/(g/1), cioè t = s/g.

Di solito, il tasso d’interesse in forma unitaria in matematica finanziaria è indicato con i.

In queste lezioni si farà diversamente: d’ora in poi, per evitare nuovi simboli, si userà r per indicare anche la forma unitaria del tasso d’interesse. Nella mia esperienza, ciò non ha mai creato difficoltà nell’apprendimento, anzi.

La formula di economia aziendale qui diventa

Gli interessi si ottengono moltiplicando il capitale per il tasso, già in forma unitaria, e per la durata, già espressa nella corretta unità di misura.

Sia chiaro che tasso e durata devono avere sempre la stessa unità di misura del tempo.

Interessi semplici e composti

Il montante è il capitale a cui sono stati aggiunti gli interessi: M = C+I. Sapendo che è I = Crt, si può sostituire, ottenendo M = C+Crt. Se si raccoglie a fattor comune, si arriva a

M = C(1+rt).

Questa è la formula di capitalizzazione semplice. Perché l’aggettivo ‘semplice’? Perché gli interessi si calcolano sempre sul “semplice” capitale iniziale e non maturano a loro volta interessi. Il regime di capitalizzazione semplice è valido di solito per calcolare gli interessi per periodi brevi; ad esempio, per un trimestre, sui conti correnti bancari.

L’argomento è già stato trattato in economia aziendale e pertanto qui non verrà ripreso seriamente. Comunque, si segnala che, volendo trovare il capitale dato il montante, bisognerà invertire la formula, ottenendo C = M/(1+rt).

Spesso, quando si lavora con quest’ultima formula, si pensa a M come ad un capitale dato futuro e a C come ad un incognito valore attuale (cioè quanto si è disposti a spendere oggi per ottenere un capitale in futuro). Questo regime è chiamato di attualizzazione semplice o di sconto razionale.

Molto più interessante, utile e sensata invece è la capitalizzazione composta, quella cioè in cui gli interessi maturano a loro volta interessi; su questa ci dilungheremo parecchio.

Calcolo di un montante composto

Per questo calcolo, si parte dall’ipotesi che il capitale maturi interessi per periodi interi, perciò sarà t = 1.

La novità, e anche la complicazione, sta nel fatto che alla fine di ogni periodo il capitale è diverso, perché comprende anche gli interessi maturati nei periodi precedenti; quindi il capitale C misurato alla fine del periodo t sarà indicato con C_t. È il caso di segnalare che C₀ indica un capitale alla fine del periodo 0, cioè all’inizio del periodo 1.

Quindi la formula di capitalizzazione è data da C_t₊₁ = C_t+rC_t, cioè, raccogliendo C_t a fattor comune, da

C_t₊₁ = C_t(1+r);

il significato è: se su un capitale C_t faccio maturare interessi per un periodo, cioè lo moltiplico per 1+r, dopo un periodo ottengo un capitale C_t₊₁.

Questa formula tuttavia non è comoda per il calcolo, perché se devo capitalizzare per 10 periodi devo ripeterne l’uso per 10 volte; e non pensiamo a quando l’incognita del problema è il tempo! Ma si può ottenere un equivalente molto migliore, nel modo che segue.

Poniamo t = 0; la formula diventa C₁ = C₀(1+r).

Poniamo t =1; la formula diventa C₂ = C₁(1+r). Ma, dato che abbiamo appena trovato qual è la formula di C₁, possiamo sostituirla e ottenere C₂ = [C₀(1+r)](1+r), cioè C₂ = C₀(1+r)².

Poniamo t = 2; la formula diventa C₃ = C₂(1+r). Ma dato che abbiamo appena trovato qual è la formula di C₂, possiamo sostituirla e ottenere C₃ = [C₀(1+r)²](1+r), cioè C₃ = C₀(1+r)³.

Continuando così, per un numero n qualunque di volte, si arriva a

C_n = C₀(1+r)ⁿ.

Questa è la formula fondamentale per i calcoli in capitalizzazione composta.

Ecco alcuni esempi di come usarla.

* Investo 2300 euro per 5 anni, al tasso del 3% annuo; di quanto disporrò alla fine?

I dati sono C₀ = 2300, n = 5, r = 3% = 0,03; il montante è quindi C₅ = 2300(1+0,03)⁵ = 2666,33 euro.

* Chiedo un prestito di 1000 euro, al tasso del 2,1% semestrale, da rimborsare in blocco fra 2 anni; quanto dovrò pagare alla fine?

I dati sono C₀ = 1000, r = 2,1% = 0,021, n = 2´2 =4 (ATTENZIONE! Il tasso è semestrale, quindi il tempo va misurato in semestri, cioè con f = 2); il montante quindi è C₄ = 1000(1+0,021)⁴ = 1086,68 euro.

* Non è obbligatorio usare questa formula soltanto in ambito finanziario: oggi compro un litro di latte con 1,30 euro; il tasso d’inflazione è di circa il 2,5%; fra 10 anni, quanto mi aspetto che costerà un litro di latte?

I dati sono C₀ = 1,3, r = 2,5% = 0,025, n = 10; il montante quindi è C₁₀ = 1,3(1+0,025)¹⁰ = 1,66 euro.

* Non è obbligatorio usare questa formula soltanto in ambito economico: in un certo parco nazionale, ci sono 14 orsi; questi si riproducono ad un tasso annuo del 2%, quanti orsi ci saranno verosimilmente fra 20 anni?

I dati sono C₀ = 14, r = 2% = 0,02, n = 20; il montante quindi è C₂₀ = 14(1+0,02)²⁰ = 20,8 orsi.

* Le lasagne, appena tolte dal forno, sono a circa 180° sopra la temperatura ambiente e si raffreddano ad un tasso del 30% ogni minuto (dato inventato); fra 8 minuti, di quanto saranno più calde della temperatura ambiente?

I dati sono C₀ = 180, r = -30% = -0,3 (ATTENZIONE! Le lasagne si raffreddano, perciò il tasso è negativo!), n = 8; il montante quindi è C₈ = 180(1-0,3)⁸ = 10,38°.

La formula può essere usata per tutti i fenomeni in cui qualcosa cambia ad un tasso costante (nell’ultimo esempio, Newton ha mostrato che la differenza di temperatura di un corpo col suo ambiente varia ad un tasso costante).

La capitalizzazione composta aumenta il montante molto più di quanto faccia la capitalizzazione semplice; ciò è tanto più evidente quanto maggiore è il tasso e quanto maggiore è il tempo di capitalizzazione.

Esempio: dato un capitale di 100 euro, qual è il montante al tasso dell’8% dopo 10 anni in regime composto? E in regime semplice?

In regime composto, si ottiene il montante C₁₀ = 100´(1+0,08)¹⁰ = 215,89.

In regime semplice, si ottiene il montante M = 100´(1+0,08´10) = 180.

Una variazione sul tema: la crescita logistica

La formula di capitalizzazione composta mostra un capitale che aumenta per sempre e sempre più velocemente. Naturalmente tutto ciò non è possibile nella realtà, ma è accettabile quando si lavora con grandezze lontane dal loro massimo possibile, come i capitali di famiglie e imprese. Se invece si lavora con grandezze per le quali il massimo possibile (che nel seguito sarà chiamato capienza) non è poi tanto lontano, l’andamento non può più essere quello della capitalizzazione composta.

Esempi: se trattiamo della crescita di una popolazione (umana, vegetale, batterica e simili) nel suo ambiente, il massimo possibile di popolazione su un dato territorio si raggiunge in tempi contenuti; se trattiamo della crescita di una pianta, la massima altezza possibile si raggiunge al massimo in decenni; se trattiamo di un’epidemia, il massimo numero di contagiati si raggiunge presto.

Ecco un modo (non l’unico, ma il più naturale) per trattare di simili fenomeni: indicando con K la capienza di una certa grandezza, la differenza K-C_t indica per quanto ancora la grandezza C_t può aumentare o, cambiando semplicemente unità di misura, le risorse di C_t ancora disponibili per l’aumento.

Quindi U_t = C_t/(K-C_t) misura la grandezza che aumenta non in assoluto, ma rispetto alle risorse ancora disponibili; questa grandezza relativa, diversamente da quella assoluta, può crescere per sempre, perché aumenta anche quando c’è una semplice riduzione di risorse disponibili. Si può anche interpretare U_t come la difficoltà con cui cresce C_t.

Poniamo che sia questa grandezza relativa, o questa difficoltà di crescita, che aumenta ad un tasso costante, perciò si ha U_t₊₁ = (1+r)U_t .

Questa formula ha la stessa struttura di C_t₊₁ = C_t(1+r), pertanto potrà essere trattata allo stesso modo e dare U_n = U₀(1+r)ⁿ.

Sostituendo U_n = C_n/(K-C_n) in questa formula, si ottiene .

Ora bisogna rendere esplicita C_n; ecco i passaggi:

* si sostituisce la pesante espressione con la semplice lettera A (passaggio lecito perché l’espressione in questione con contiene l’incognita C_n), in modo da ridurre la formula sopra alla più semplice

* si isola C_n, mediante i passaggi che seguono:

* si moltiplica ambo i membri per K-C_n , ottenendo ;

* si svolge la parentesi con C_n , ottenendo ;

* si portano a sinistra i termini con C_n e a destra quelli senza, ottenendo ;

* si raccoglie a fattor comune C_n, ottenendo ;

* si divide ambo i membri per la parentesi, ottenendo ;

* una volta ultimati i calcoli per isolare C_n, si reintroduce al posto di A l’intera espressione , arrivando a

;

* si nota che la frazione C₀/(K-C₀) è al denominatore, quindi può essere “ribaltata”; inoltre, si può usare un esponente negativo per 1+r, ottenendo finalmente

Questa funzione di n si chiama logistica e mostra come può cambiare una crescita esponenziale, come ad esempio la capitalizzazione composta, quando la grandezza che cresce ha una capienza.

Esempio: il tasso per periodo a cui cresce una popolazione di 10 batteri è il 25%. Indicare la quantità di batteri dopo 20 periodi, sia in un ambiente illimitato, sia in un ambiente in cui al massimo possono stare 1000 batteri.

I dati sono: C₀ = 10, r = 25% = 0,25, n = 20, K = 1000; nell’ambiente illimitato, si ha un montante di C₂₀ = 10(1+0,25)²⁰ = 867,36; nell’ambiente con capienza 1000, si ha .

Esempio: la popolazione di un certo comune con forte immigrazione oggi ha 41.456 residenti, mentre 8 anni fa ne aveva 39.665. Se il tasso di crescita è il 2% annuo, qual è la capienza del comune? Cioè, a quante persone si presume che possa arrivare?

Dati: n = 8, C₈ = 41.456, C₀ = 39.665, r = 0,02.

Conviene cominciare a isolare K prendendo la formula nella forma .

Spostando i termini con K a sinistra dell’uguale, gli altri a destra e raccogliendo K a fattor comune, si ha .

Chi non volesse usare esponenti negativi, può sempre moltiplicare numeratore e denominatore per (1+r)ⁿ, ottenendo .

Sostituendo ora i dati, si ottiene .

Le formule inverse per la capitalizzazione composta

Torniamo alla formula di capitalizzazione composta. In essa ci sono quattro variabili, C_n, C₀, r e n, ciascuna delle quali è una possibile incognita.

* Se l’incognita è C_n, basta la solita formula diretta di capitalizzazione composta.

Gli esempi sopra illustrano bene il punto.

* Se l’incognita è C₀, basta dividere per (1+r)ⁿ per ottenere

Esempio: fra 3 anni, incasserò un credito di 3000 euro; se voglio avere subito denaro liquido e sconto il credito in banca al 4%, quanto ottengo?

Dati: n = 3; C₃ = 3000, r = 4% = 0,04; il valore attuale è C₀ = 3000/(1+0,04)³ = 2666,99 euro.

In certi problemi, non è facile capire se ciò che si deve trovare è C₀ o C_n. Ecco uno schema che può favorire la decisione giusta.

Disegnamo l’asse del tempo, che va sempre da sinistra (passato) a destra (futuro), con le formule da usare nei vari casi.

Asse del tempo: Passato ®®®®®®®®®®®® Presente ®®®®®®®®®®®® Futuro

Formule da usare:

CAPITALE ® MONTANTE « VALORE ATTUALE ¬ CAPITALE

(passato) (presente) (futuro)

* Se l’incognita è r, servono 3 passaggi: primo, si divide ambo i membri per C₀, ottenendo (si prende sempre col segno positivo, perché 1+r negativo non ha molto senso); terzo, si sottrae 1 da ambo i membri, ottenendo

Esempio: il valore nominale dei BOT è convenzionalmente 100, mentre il loro valore di mercato è minore di 100; se ad esempio un BOT costa tutto compreso 97,8 e mancano 240 giorni alla scadenza, qual è il tasso annuo effettivo d’interesse?

Dati: n = 240/365 (se il tasso è annuo, bisogna convertire il tempo in anni) = 0,657534; C_0,657534 = 100, C₀ = 97,8.

Il tasso è .

Esempio: compro un titolo a 130 e dopo un anno lo rivendo a 110. Qual è il tasso di profitto annuo?

Dati: C₀ = 130; n = 1; C₁ = 110.

Il tasso è r = (110/130)-1 = -0,1539. Si ha quindi un tasso di perdita del 15,39%.

* Se l’incognita è n, servono questi passaggi: primo, si divide ambo i membri per C₀, ottenendo ; secondo, si esplicita n, ottenendo n = log_(1+r)(C_n/C₀); terzo, si cambia la base, ottenendo

Esempio: investo 2500 euro al 2,5% annuo; se mi servono 3000 euro, fra quanto tempo potrò incassare?

Dati, C₀ = 2500, r = 3% = 0,025, C_n = 3000; il tempo (in anni) è .

Questo risultato è in anni, ma a me serve convertirlo in anni, mesi e giorni; perciò comincio a notare che stiamo trattando di 7 anni e di una quota di anno pari a 0,38365; a quanto corrisponde in mesi? a 0,38365´12, cioè 4,6038 mesi; abbiamo quindi 4 mesi e una quota di mese pari a 0,6038; quanto fa in giorni? Assumendo l’anno commerciale, si ha 0,6038´30, cioè 18,114 giorni, che si può approssimare a 18 giorni, dato che le scadenze dei contratti di credito si misurano in date e non in orari.

I tassi equivalenti

Tasso e durata devono sempre essere nella stessa unità di misura: se il tasso è annuo, la durata è in anni; se il tasso è mensile, la durata è in mesi; e così via. Finora si è trattato il caso in cui si teneva fissa l’unità di misura del tasso e si faceva variare quella della durata, ma ora si mostrerà che è possibile anche l’inverso.

Il punto è che il tasso con una certa frequenza deve risultare del tutto equivalente a quello con un’altra frequenza. Quando due tassi sono equivalenti? Quando, partendo dallo stesso capitale, danno lo stesso montante.

Se ho un certo capitale C e voglio investirlo per un anno con capitalizzazione di frequenza f, con un tasso r_f otterrò un certo montante M; in formule, M = C(1+r_f)^f.

Se cambia la frequenza, che diventa g, ma voglio partire dallo stesso capitale C per arrivare allo stesso montante M, dovrò cambiare il tasso in un nuovo tasso r_g; in formule, M = C(1+r_g)^g.

Dato che entrambi i montanti sono uguali a M, le capitalizzazioni saranno anch’esse uguali, perciò si ha C(1+r_f)^f = C(1+r_g)^g.

Semplificando C, si ottiene

(1+r_f)^f = (1+r_g)^g.

Volendo esplicitare r_f, si ha, con i soliti calcoli per le formule inverse,

r_f= (1+r_g)^g^/f-1.

Esempio: qual è il tasso annuo che equivale al 4% trimestrale?

Si cerca r_f, perciò è f = 1; si ha r_g = 0,04, perciò è g = 4; quindi risulta r₁ = (1+0,04)^4/1-1 = 0,1699 = 16,99% annuo.

Esempio: qual è il tasso mensile che equivale al 3,5% semestrale?

Si cerca r_f, perciò è f = 12; si ha r_g = 0,035, perciò è g = 2; quindi risulta r₁₂ = (1+0,035)^2/12-1 = 0,00575 = 0,575% mensile.

Esempio: qual è il tasso biennale che equivale al 5,5% annuo?

Si cerca r_f, perciò è f = 0,5; si ha r_g = 0,055, perciò è g = 1; quindi risulta r_0,5 = (1+0,055)^1/0,5-1 = 0,113 = 11,3% annuo.

SCHEDE DI MATEMATICA FINANZIARIA 2

Quando intervengono più importi

I problemi finora sono stati piuttosto semplici, ma anche poco realistici: le operazioni finanziarie possono coinvolgere più movimenti di una sola entrata e una sola uscita. In tal caso, bisogna capire come mettere insieme tutti i dati. Ecco una scaletta utile e abbastanza generale; ma bisogna comunque essere attenti a portare eventuali adattamenti allo schema, in presenza di problemi particolari.

1 Anzitutto, bisogna trovare l’ordine temporale in cui vanno messi tutti i movimenti; più sono nel passato, più vanno a sinistra; più sono nel futuro, più vanno a destra.

2 Poi bisogna decidere in che momento stiamo eseguendo i nostri calcoli: prima di tutti i movimenti? Dopo tutti i movimenti? In qualche punto in mezzo?

3 Stabilito ciò, bisogna capitalizzare i movimenti nel passato (infatti, durante il passato sono stati accumulati interessi) e attualizzare quelli nel futuro (infatti, gli interessi futuri non sono ancora stati ottenuti).

4 Una volta capitalizzati o attualizzati, i movimenti vanno sommati, se sono entrate, o sottratti, se sono uscite, in modo da formare i totali impliciti nel problema.

5 Infine, i movimenti vanno confrontati, impiegando il segno di uguale (più di rado, almeno negli esercizi, i segni di maggiore o minore); in tal modo si ottiene un’equazione, che va risolta, rispondendo al problema.

Esempio: dobbiamo pagare 3 debiti, tutti al tasso annuo del 6%: il primo è di 10.000 euro e scade fra 3 anni; il secondo è di 25.000 euro e scade fra 5 anni; il terzo è di 17.000 euro e scade fra 6 anni. Volendo rimborsare tutto con un unico pagamento fra 2 anni, qual è l’importo x da pagare?

Primo: ordinare cronologicamente gli importi. L’ordine è x, 10.000, 25.000, 17.000.

Secondo: determinare quando è oggi. Oggi è 2 anni prima di x. Da ciò segue questo schema.

Importo	-	-x	-10.000	-25.000	-17.000
Tempo	0	2	3	5	6

Terzo: i movimenti sono tutti nel futuro, perciò vanno tutti attualizzati.

Quarto: i movimenti sono tutti uscite, perciò vanno tutti sottratti; infatti sono stati scritti con il meno. Il movimento .

Quinto: nella consegna è implicito, ma inevitabile, che il pagamento unico con x sostituisca i 3 pagamenti con 10.000, 25.000 e 17.000. Chiaramente, in matematica una sostituzione è possibile soltanto quando ciò che è sostituito è uguale a ciò che sostituisce. Quindi si deve costruire l’equazione .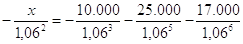

Il grosso del problema, anzi, la parte specifica della matematica finanziaria, finisce qui. Tuttavia, bisogna ancora trovare il valore di x, con un po’ di algebra: basta moltiplicare ambo i membri per –1,06² per ottenere . Ora bisogna proprio fare i conti sul membro destro, che portano a x = 43.890,04.

Esempio: 3 anni fa ho depositato 3000 euro in una banca che dà un tasso del 3% annuo; un anno dopo, ho prelevato 1000 euro. Quanto devo versare oggi, per trovare fra un anno sul conto corrente 3500 euro?

Primo: ordinare nel tempo gli importi. Si ha 3000, 1000, x, 3500.

Secondo: determinare quando è oggi. Oggi è il giorno in cui si paga x. Da ciò segue questo schema.

Importo	3000	-1000	x	3500
Tempo	-3	-2	0	1

Terzo: vanno capitalizzati i primi due movimenti e attualizzato il quarto, mentre il terzo non va né capitalizzato né attualizzato, perché non è né passato né futuro: lo si lascia com’è.

Quarto e quinto: l’unica uscita dal conto corrente è il secondo movimento, infatti è già stato scritto col meno. I primi tre movimenti devono dare il quarto, perciò si ha . Il risultato dell’equazione è x = 1180,78.

Esempio: 2 anni fa, ho prestato 3000 euro al 4%; quando è il momento del rimborso, uso il denaro per estinguere un mio debito di 3500 euro al 3%, che scadrà fra 2 anni. Quando mi è stato o mi sarà rimborsato il denaro?

Primo: l’ordine è 3000, 3500.

Secondo: oggi è in un momento intermedio fra i due movimenti, perciò lo schema è questo.

Importo	-3000	-	-3500
Tempo	-2	0	2

Non scrivo l’incognita, perché riguarda il tempo, perciò non so dove collocarla.

Terzo: si capitalizza il primo movimento e si attualizza il secondo.

Quarto: che il 3000 sia un’uscita è chiaro; ma lo è anche il 3500, perché si tratta di un rimborso che devo fare, sia pure anticipatamente.

Quinto: conviene fissare le idee e immaginare che il rimborso capiti in qualche momento del futuro (se non sarà così, semplicemente il tempo avrà un segno negativo), in modo da ottenere che il montante del mio credito sia uguale al valore attuale del mio debito: .

Anche qui la parte specifica della matematica finanziaria è finita, ma c’è ancora da risolvere l’equazione.

Intanto si può dividere ambo i membri per -1000, in modo da ottenere .

Poi bisogna portare tutti i termini con le x da un lato (per fissare le idee, a sinistra) dell’uguale e tutti i termini noti dall’altro, quindi, tanto per cominciare, 1,03²^-x×1,04^2+x = 3,5/3.

Ora c’è da gestire il membro sinistro; a questo scopo si usano le proprietà delle potenze: .

Ancora, tutti i termini noti vanno spostati a destra, in modo da ottenere .

Usando ancora le proprietà delle potenze e svolgendo i calcoli al membro destro, si ha .

La frazione fra parentesi vale 1,009709, perciò l’equazione diventa 1,009709^x = 1,01673.

Usando i logaritmi, si trova x = log₁₀1,01673/log₁₀1,009709 = 1,717222.

Con facile conversione, si trova 1 anno, 8 mesi e 18 giorni (anno commerciale).

In tutti i problemi, si tratta sempre di costruire formule, portando tutti i termini a sinistra dell’uguale, con la struttura , in cui tutte le grandezze sono date tranne una; la grandezza che manca è l’incognita da trovare per far tornare i conti.

L’importante è usare attenzione nel costruire la formula; ecco alcuni punti importanti da considerare.

* Convertire i tassi percentuali in unitari.

* Usare la stessa unità di misura per il tempo e per i tassi.

* Scrivere le entrate con il + e le uscite con il -.

* Capire quali movimenti sono futuri, quali passati e quali presenti.

* Non capitalizzare e non attualizzare i movimenti presenti.

* Se si privilegia l’attualizzazione, e quindi si scrive come sopra C/(1+r)ⁿ, scrivere i tempi futuri con il + e quelli passati con il -, usando poi la definizione di esponente negativo.

Volendo, si può anche privilegiare la capitalizzazione, e quindi scrivere diversamente da sopra C(1+r)ⁿ, ma allora bisogna scrivere i tempi passati con il + e quelli futuri con il -, usando poi la definizione di esponente negativo.

O, infine, si può scrivere i termini futuri come C/(1+r)ⁿ e quelli passati come C(1+r)ⁿ, senza bisogno di segni negativi.

Quando il tasso non è costante

Finora si è trattato dei casi in cui si hanno tanti movimenti, ma ciascuno usa un solo tasso di capitalizzazione (o di attualizzazione). Ora si tratterà il caso di un solo movimento, che può avere più tassi di capitalizzazione (o di attualizzazione).

Si consideri un capitale C che per un periodo t₁ matura interessi a un tasso r₁, poi per un successivo periodo t₂ matura interessi ad un tasso r₂ e così via fino a un periodo t_n, in cui gli interessi maturano ad un tasso r_n. Il montante sarà ottenuto mettendo insieme tutte le capitalizzazioni:

D’altronde, è naturale: il capitale C comincia ad essere capitalizzato al tasso r₁, arrivando a ; il procedimento si ripete per ogni tasso, finché si arriva alla capitalizzazione totale indicata sopra.

Esempio: un capitale di 6000 euro viene investito al 4%; dopo un anno, il tasso scende al 3,5%; dopo due anni, scende di un altro punto percentuale; qual è il montante dopo 10 anni complessivi di capitalizzazione?

Dati: C = 6000, t₁ = 1, r₁ = 4%, t₂ = 2, r₂ = 3,5%, t₃ = 10-1-2 = 7, r₃ = 3,5%-1% = 2,5%. Quindi il montante è M = 6000´1,04´1,035²´1,025⁷ = 7945,70.

Le progressioni geometriche

Sono trattate anche nel libro.

Per la dimostrazione del valore di S_n si offre qui una variante del libro: sapendo che sono a₂ = a₁q, a₃ = a₁q², a₄ = a₁q³ e così via, la somma S_n = a₁+a₂+a₃+...+a_n è uguale a a₁+a₁q+a₁q²+...+a₁qⁿ^-1.

Raccogliendo a fattor comune, si ottiene S_n = a₁(1+q+q²+...+qⁿ^-1).

Moltiplicando questa uguaglianza per q, si ottiene qS_n = a₁(q+q²+q³+...+qⁿ).

Sottraendo ora la seconda uguaglianza dalla prima, tutti i termini da q fino a qⁿ^-1 si semplificano, perché si ha

S_n = a₁(1+q+q²+...+qⁿ^-1 ) -

qS_n = a₁( q+q²+...+qⁿ^-1+qⁿ) =

______________________________.

S_n-qS_n = a₁(1 - qⁿ)

Ci si trova quindi con l’equazione S_n-qS_n = a₁(1-qⁿ), in cui bisogna esplicitare S_n ; basta raccoglierla a fattor comune e dividere ambo i membri per la parentesi tonda, arrivando al risultato del libro, cioè

Ha un certo valore il caso in cui n tende a ¥.

Se è -1 < q < 1, che è il caso più utile, allora qⁿ tende a zero e si ottiene a₁(1+q+q²+q³+...) = a₁/(1-q).

Se è q > 1, allora qⁿ tende a infinito e si ottiene a₁(1+q+q²+q³+...) = ¥.

Se è q < -1, allora qⁿ oscilla fra ¥ e -¥ e a₁(1+q+q²+q³+...) non ha alcun valore.

Le rendite certe

Le progressioni geometriche sono utili per semplificare i calcoli, quando i problemi di matematica finanziaria trattano di lunghe successioni di importi (rendite), costanti o in progressione geometrica. Il punto è chiarito entrando subito nel merito.

Accumulo di capitali (rendite con capitale finale)

Ogni periodo riesco a mettere da parte una rendita costante R, che investo al tasso periodale r; dopo n periodi, che capitale C ottengo?

Il problema, esposto in questi termini, non è ancora ben definito; il punto essenziale è capire dopo quanto tempo dall’ultimo versamento R si calcola il capitale. Si supponga perciò che il capitale sia determinato in concomitanza con l’ultimo versamento.

In tal caso, per calcolare il legame fra C e R conviene ragionare a ritroso: l’ultima rendita R è versata quando si determina il capitale, perciò non fa in tempo a maturare interessi; il contributo al capitale fornito dall’ultima rendita è quindi semplicemente R.

A questa va aggiunta la penultima rendita, che ha potuto maturare interessi per l’ultimo periodo; il suo contributo al capitale quindi è R(1+r).

Poi va aggiunta la terz’ultima rendita, che ha potuto maturare due periodi di interessi, quindi il suo contributo è R(1+r)².

Per la quart’ultima rendita, il contributo al capitale è R(1+r)³ e così via.

Dato che le rendite in totale sono n, la prima rendita ha potuto accumulare interessi per n-1 periodi, perciò il suo contributo è R(1+r)ⁿ^-1.

In totale, si ha C = R+R(1+r)+R(1+r)²+...+R(1+r)ⁿ^-1.

Il passo più importante è stato fatto, perché la formula appena trovata permette di rappresentare e risolvere il problema, ma la sua forma è scomoda; è qui che torna utile conoscere le progressioni geometriche. Si riporta per comodità il risultato essenziale trovato a suo tempo:

Ora si può cominciare ad elaborare la formula sulle rendite. Anzitutto, conviene raccogliere a fattor comune R, ottenendo C = R[1+(1+r)+(1+r)²+...+(1+r)ⁿ^-1].

Se invece di 1+r scriviamo q, la parentesi quadra appare come [1+q+q²+...+qⁿ^-1].

Abbiamo la formula per le progressioni geometriche, in cui non appare a₁, cioè in cui è a₁ = 1.

La formula sulle rendite quindi si può scrivere come C = R[1+q+q²+...+qⁿ^-1] o anche come , che dà subito

Il coefficiente si indica spesso anche con s_n_|r e si legge “esse figurato”. In realtà, quando è stampato c’è anche una linea orizzontale sopra la n, che è scomoda da riprodurre in Word e perciò qui viene omessa.

Esempio: riesco a mettere da parte 120 euro ogni mese, ad un tasso mensile dello 0,4%; che capitale avrò fra un anno, nel momento in cui pago l’ultima rendita?

Dati: R = 120, r = 0,4% = 0,004, n = 12; il capitale quindi è C = 120[(1+0,004)¹²-1]/0,004 = 1472,11 euro.

Esempio: mi serve un capitale di 5000 euro fra 3 anni; con un tasso del 2% annuo, quanto devo mettere da parte ogni mese (sempre nell’ipotesi che il capitale si determini con l’ultima rendita)?

Dati: C = 5000, n = 3´12 = 36 (i versamenti sono mensili, perciò bisogna trasformare tutto in mesi), r = (1+0,02)^1/12-1 = 0,001652 (anche qui serve l’equivalente mensile); la rendita quindi si ottiene da ed è R = 5000/12,10963 = 412,89 euro.

Esempio: deposito 300 euro tutti i mesi per 2 anni, ad un tasso mensile dello 0,15%; che capitale avrò un semestre dopo l’ultimo versamento?

Dati: R = 300, n = 2´12 = 24, r = 0,0015, dilazione dopo l’ultima rendita (chiamiamola d) = 6.

Qui non basta calcolare il capitale all’ultima rendita, ma bisogna anche tener conto che questo capitale starà a maturare interessi per altri 6 mesi. Il capitale all’ultima rendita sarebbe C = 300(1,0015²⁴-1)/0,0015 = 7325,58 euro; il capitale dopo i 6 mesi di dilazione diventa 7325,58(1+0,0015)⁶ = 7391,76 euro. Questa procedura corrisponde alla formula .

Gli ammortamenti (rendite con capitale iniziale)

Oggi ottengo un capitale C, che dovrò restituire con pagamenti costanti a cominciare dal prossimo periodo, per n periodi a un tasso r. Qual è l’ammontare R di ogni pagamento?

Il capitale C deve valere quanto la somma di tutti i valori attuali dei pagamenti R; perciò il problema si rappresenta con

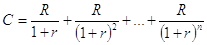Anche in questo caso, la formula può essere migliorata mediante le progressioni geometriche.

Anzitutto si raccoglie R a fattor comune, ottenendo .

Sostituendo q a 1/(1+r), si ottiene [q+q²+...+qⁿ] o anche, raccogliendo una q, q[1+q+...+qⁿ^-1].

Questa è la formula per le progressioni geometriche, in cui è a₁ = q. La formula dell’ammortamento quindi si può scrivere come C = Rq[1+q+q²+...+qⁿ^-1] o anche come .

Da qui i passaggi sono semplici: da ; semplificando e sistemando i termini, si arriva a

Il coefficiente si indica spesso anche con a_n_|r e si legge “a figurato”. In realtà, quando è stampato c’è anche una linea orizzontale sopra la n, che è scomoda da riprodurre in Word e perciò qui viene omessa.

Esempio: di che capitale deve disporre un sedicenne per vivere di rendita?

Naturalmente, bisogna circostanziare: stabiliamo che per vivere con una certa tranquillità servano indicativamente 15.000 euro all’anno, che i tassi d’interesse annui siano sul 3% e che ci si aspetti di campare almeno fino a novant’anni, perciò altri 84 anni. Allora il problema prende la forma . Quindi serve poco meno di mezzo milione di euro.

Esempio: lo stesso, ma con un tasso d’inflazione w pari al 2,5%. Qui serve un po’ di acutezza: mentre gli interessi aumentano il potere l’acquisto delle rate, l’inflazione lo diminuisce; perciò, mentre le rate attualizzate vengono divise per 1+r, le stesse rate attualizzate vanno moltiplicate per 1+w.

In pratica, invece di avere 1/(1+r), si avrà (1+w)/(1+r), perciò invece di 1+r si avrà (1+r)/(1+w) e invece di r si avrà (1+r)/(1+w)-1 = (r-w)/(1+r).

Quindi, nel nostro problema, basta usare (0,03-0,025)/1,03 = 0,004854 invece di 0,03 e il risultato diventa 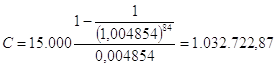; il capitale necessario risulta più del doppio rispetto al caso senza inflazione!

I piani di ammortamento

Tratteremo soltanto dei piani di ammortamento a rata costante (francese, progressivo) e a quota capitale costante (italiano); il primo perché è applicato alla stragrande maggioranza dei prestiti, il secondo per avere una comprensione più completa del problema.

In un piano di ammortamento, si indica nei particolari che cosa succede al prestito, rata per rata. In particolare, nel piano di ammortamento conviene che siano presenti le seguenti voci: numero della rata, capitale prima di aver pagato la rata, importo della rata, quota interessi, quota capitale, capitale dopo aver pagato la rata.

Obiezione: una volta stabilito l’importo che il debitore deve pagare, a che serve un piano d’ammortamento esposto nei particolari? Serve perché tutta la mole di calcolo permette di separare, all’interno della rata, le quote interesse dalle quote capitale e questa separazione ha almeno tre motivi pratici per essere attuata.

* Chi intende rimborsare un prestito in anticipo, deve sapere quanto capitale gli resta da restituire; tale capitale è dato dal capitale iniziale meno la somma di tutte le quote capitale. Se non si conoscono le quote capitale, il calcolo è impossibile.

* Il fisco concede agevolazioni per alcune categorie di mutui ipotecari, misurate sul totale di interessi pagati in un anno; tali interessi si possono determinare soltanto conoscendo le quote interessi.

* I mutui a tasso indicizzato, in genere, sono fatti in modo che la quota capitale di ogni rata sia quella stabilita per contratto, mentre la quota interessi varia di volta in volta, secondo l’andamento di mercato dei tassi d’interesse. Conoscere la composizione della rata è quindi essenziale per calcolarla.

Per determinare il piano d’ammortamento, servono i dati contrattuali che stabiliscono le condizioni del prestito, cioè il capitale prestato C, il tasso r, la durata n e la periodicità di pagamento, che va convertita in frequenza, cioè in numero di rate all’anno.

Il capitale è di immediata lettura.

Di solito, la durata è in anni e va convertita in numero di rate, perciò moltiplicata per la frequenza. Ad esempio, un mutuo ventennale con rate mensili ha una durata n = 20´12 = 240.

Anche il tasso non è periodale; viene fornito come TAN, cioè tasso annuo nominale, e va diviso per la frequenza; ad esempio, se il TAN è il 6% e le rate semestrali, è r = 0,06/2 = 0,03.

Qualcuno obietterà: ma il tasso equivalente non si calcola così. Vero, ma il tasso equivalente sarebbe minore e le banche guadagnerebbero meno, pertanto adottano il metodo brutale sopra. Nell’esempio appena mostrato, il tasso equivalente sarebbe 0,0296.

La periodicità non ha un impiego diretto, ma viene usata per determinare tasso e durata.

Costruzione di un ammortamento francese, con un esempio

Un contratto dà: capitale di 100.000 euro, in 10 anni, con TAN = 5% e periodicità semestrale.

Anzitutto, si determina la durata, cioè n = 10´2 = 20, e il tasso, cioè r = 0,05/2 = 0,025; poi si comincia a stendere il piano d’ammortamento.

Capitale prima di aver pagato la prima rata: è il capitale prestato, cioè 100.000.

Prima rata: la caratteristica di questo piano è la rata costante; in altri termini, bisogna che il capitale sia equivalente all’insieme di tutte le rate da pagare e queste rate sono tutte uguali fra loro; bisogna poi tener conto che le rate saranno pagate in futuro, perciò bisogna attualizzarle. In sostanza, si ottiene quanto già mostrato per le rendite con capitale iniziale, perciò la formula che lega capitale e rate è ; la rata quindi si ottiene dal capitale esplicitando R, cioè con la formula inversa R = 100.000/a_20|0,025 = 6414,71.

Prima quota interessi: gli interessi si calcolano con la formula 100.000´0,025t, ma qui è t = 1, perché il tasso si applica su un intero periodo di pagamento, perciò la quota interessi è determinata da 100.000´0,025 = 2500.

Prima quota capitale: dato che la rata è costituita da quota interessi e quota capitale, per trovare la quota capitale basta togliere la quota interessi dalla rata: 6414,71-2500 = 3914,71.

Capitale dopo il pagamento della prima rata: dal capitale prima di aver pagato la rata, va tolta la quota capitale, perciò si ha 100.000-3914,71 = 96.085,29.

Capitale prima di pagare la seconda rata: è il capitale dopo aver pagato la prima rata, cioè 96.085,29.

Seconda rata: l’ammortamento è a rate costanti, perciò tutte le rate sono uguali; si ripete quindi 6414,71.

Seconda quota interessi: ora gli interessi vanno calcolati sul debito attuale, che è 96.085,29; perciò la quota è 96.085,29´0,025 = 2402,13.

Seconda quota capitale: è 6414,71-2402,13 = 4012,58.

Capitale dopo il pagamento della seconda rata: si toglie l’ultima quota capitale calcolata dal capitale restante: 96.085,29-4012,58 = 92072,71.

Per la terza rata, si continua allo stesso modo della seconda. Si finirà alla ventesima rata, quando il capitale dopo aver pagato la rata sarà 0. Ecco il piano al completo.

Periodi	Capitale prima di aver pagato la rata	Rata	Quota interessi	Quota capitale	Capitale dopo aver pagato la rata
1	100.000,00	6.414,71	2.500,00	3.914,71	96.085,29
2	96.085,29	6.414,71	2.402,13	4.012,58	92.072,71
3	92.072,71	6.414,71	2.301,82	4.112,90	87.959,81
4	87.959,81	6.414,71	2.199,00	4.215,72	83.744,09
5	83.744,09	6.414,71	2.093,60	4.321,11	79.422,98
6	79.422,98	6.414,71	1.985,57	4.429,14	74.993,84
7	74.993,84	6.414,71	1.874,85	4.539,87	70.453,98
8	70.453,98	6.414,71	1.761,35	4.653,36	65.800,61
9	65.800,61	6.414,71	1.645,02	4.769,70	61.030,92
10	61.030,92	6.414,71	1.525,77	4.888,94	56.141,98
11	56.141,98	6.414,71	1.403,55	5.011,16	51.130,81
12	51.130,81	6.414,71	1.278,27	5.136,44	45.994,37
13	45.994,37	6.414,71	1.149,86	5.264,85	40.729,52
14	40.729,52	6.414,71	1.018,24	5.396,47	35.333,04
15	35.333,04	6.414,71	883,33	5.531,39	29.801,66
16	29.801,66	6.414,71	745,04	5.669,67	24.131,98
17	24.131,98	6.414,71	603,30	5.811,41	18.320,57
18	18.320,57	6.414,71	458,01	5.956,70	12.363,87
19	12.363,87	6.414,71	309,10	6.105,62	6.258,26
20	6.258,26	6.414,71	156,46	6.258,26	0,00

Si dà ora lo sviluppo in formule.

Periodi	Capitale prima di aver pagato la rata	Rata	Quota interessi	Quota capitale	Capitale dopo aver pagato la rata
1	C₀ = C	R = C/a_n_\|r	I₁ = C₀r	Q₁ = R-I₁	C₁ = C₀-Q₁
2	C₁	R	I₂ = C₁r	Q₂ = R-I₂	C₂ = C₁-Q₂
3	C₂	R	I₃ = C₂r	Q₃ = R-I₃	C₃ = C₂-Q₃
...	...	...	...	...	...

Queste formule permettono di trovare un modo veloce di calcolare una qualunque quota capitale.

Se si scompone una rata nelle sue quote, si trova R = Q_t+I_t o, volendo, anche R = Q_t₊₁+I_t₊₁.

Confrontando le due uguaglianze, si ha Q_t+I_t = Q_t₊₁+I_t₊₁.

La formula si può anche scrivere come I_t₊₁-I_t = Q_t-Q_t₊₁.

Dato che è I_t = rC_t_-1, i termini a sinistra dell’uguale si possono anche scrivere come rC_t-rC_t_-1 o, raccogliendo r a fattor comune, come r(C_t-C_t_-1).

La differenza C_t_-1-C_t è proprio la quota capitale Q_t, perciò è C_t-C_t_-1 = -Q_t. Il termine a sinistra dell’uguale è quindi -rQ_t.

Sostituendolo nell’uguaglianza, si ha -rQ_t = Q_t-Q_t₊₁, che riscritta dà Q_t₊₁ = (1+r)Q_t.

Ponendo successivamente t = 1, t = 2 e così via, come si è fatto costruendo la formula per la capitalizzazione composta, si ottiene Q_t = Q₁(1+r)^t^-1.

Dato che è Q₁ = R-rC, si arriva a trovare

Q_t = (R-Cr)(1+r)^t^-¹.

Costruzione di un ammortamento italiano, con un esempio

Nell’ammortamento italiano, quello che resta costante è la quota capitale. Se le quote capitale messe insieme fanno il capitale e sono tutte uguali, per determinarle basta dividere il capitale per il numero di rate. Le rate saranno determinate sommando le quote capitale alle quote interessi. Gli altri importi si determinano come nell’ammortamento francese. Ecco come si sviluppa un ammortamento italiano con gli stessi dati già usati per il francese.

Periodi	Capitale prima di aver pagato la rata	Quota capitale	Quota interessi	Rata	Capitale dopo aver pagato la rata
1	100.000,00	5.000,00	2.500,00	7.500,00	95.000,00
2	95.000,00	5.000,00	2.375,00	7.375,00	90.000,00
3	90.000,00	5.000,00	2.250,00	7.250,00	85.000,00
4	85.000,00	5.000,00	2.125,00	7.125,00	80.000,00
5	80.000,00	5.000,00	2.000,00	7.000,00	75.000,00
6	75.000,00	5.000,00	1.875,00	6.875,00	70.000,00
7	70.000,00	5.000,00	1.750,00	6.750,00	65.000,00
8	65.000,00	5.000,00	1.625,00	6.625,00	60.000,00
9	60.000,00	5.000,00	1.500,00	6.500,00	55.000,00
10	55.000,00	5.000,00	1.375,00	6.375,00	50.000,00
11	50.000,00	5.000,00	1.250,00	6.250,00	45.000,00
12	45.000,00	5.000,00	1.125,00	6.125,00	40.000,00
13	40.000,00	5.000,00	1.000,00	6.000,00	35.000,00
14	35.000,00	5.000,00	875,00	5.875,00	30.000,00
15	30.000,00	5.000,00	750,00	5.750,00	25.000,00
16	25.000,00	5.000,00	625,00	5.625,00	20.000,00
17	20.000,00	5.000,00	500,00	5.500,00	15.000,00
18	15.000,00	5.000,00	375,00	5.375,00	10.000,00
19	10.000,00	5.000,00	250,00	5.250,00	5.000,00
20	5.000,00	5.000,00	125,00	5.125,00	-

Si dà ora lo sviluppo in formule.

Periodi	Capitale prima di aver pagato la rata	Quota capitale	Quota interessi	Rata	Capitale dopo aver pagato la rata
1	C₀ = C	Q = C/n	I₁ = C₀r	R₁ = Q+I₁	C₁ = C₀-Q
2	C₁	Q	I₂ = C₁r	R₂ = Q+I₂	C₂ = C₁-Q
3	C₂	Q	I₃ = C₂r	R₃ = Q+I₃	C₃ = C₂-Q
...	...	...	...	...	...

Fonte:

http://schedematematica.wikispaces.com/file/view/SCHEDE%20DI%20MATEMATICA%20FINANZIARIA%201.doc

http://schedematematica.wikispaces.com/file/view/SCHEDE%20DI%20MATEMATICA%20FINANZIARIA%202.doc

Sito web da visitare :http://schedematematica.wikispaces.com/

Autore del testo: non indicato nel documento di origine

Parola chiave google : Matematica finanziaria tipo file : doc

Matematica finanziaria