Frazioni numeriche
Frazioni numeriche
I riassunti, le citazioni e i testi contenuti in questa pagina sono utilizzati per sole finalità illustrative didattiche e scientifiche e vengono forniti gratuitamente agli utenti.
Le Frazioni |
La frazione è un operatore che opera su una qualsiasi grandezza e che dà come risultato una grandezza omogenea a quella data.
Esempio:
se un segmento AB è stato diviso in tre parti e se ne prendono due, si dice che si considerano i due terzi del segmento.
Una frazione è formata da un numeratore e da un denominatore, divisi da una linea detta linea di frazione.
Una frazione divide una grandezza in tante parti quanto è indicato dal denominatore e ne prende tante quante è indicato dal numeratore.
Le frazioni equivalenti
Due frazioni sono equivalenti quando applicate alla stessa grandezza danno lo stesso risultato.
Una frazione può essere trasformata in un’altra equivalente moltiplicando o dividendo il numeratore e il denominatore per uno stesso numero diverso da zero. Questa proprietà è detta proprietà invariantiva delle frazioni.
La semplificazione di una frazione
Per semplificare una frazione si dividono il numeratore e il denominatore per un divisore comune.
Una frazione si dice ridotta ai minimi termini quando il numeratore e il denominatore sono primi tra loro.
Una frazione per essere ridotta ai minimi termini deve essere semplificata per il M.C.D. tra il numeratore e il denominatore.
Tipi di frazione
Ci sono tre tipi di frazioni:
- Frazioni proprie: il numeratore è minore del denominatore (quindi la frazione è <1)
- Frazioni improprie: il numeratore è maggiorere del denominatore (la frazione risulta >1)
- Frazioni apparenti: il numeratore è multiplo del denominatore (quindi la frazione è uguale a un numero intero)
TRASFORMAZIONE DI PIU' FRAZIONI IN FRAZIONI EQUIVALENTI AVENTI LO STESSO DENOMINATORE
Per trasformare due o più frazioni in frazioni equivalenti con lo stesso denominatore, si deve scegliere come denominatore comune il m.c.m. tra i denominatori delle frazioni. Si deve poi dividere il nuovo denominatore per il vecchio denominatore e moltiplicare il risultato ottenuto per il vecchio numeratore, ottenendo così il nuovo numeratore.
La trasformazione serve per le operazioni e per il confronto di frazioni.
Addizione di frazioni
1) Addizione di frazioni con stesso denominatore:
Si sommano i numeratori e si conservano i denominatori
2) Addizione di frazioni con denominatori diversi:
Si applica la trasformazione di più frazioni in frazioni equivalenti con lo stesso denominatore e poi si somma come nel caso 1.
3) Addizione di un numero intero con una frazione:
Si deve moltiplicare il numero intero per il denominatore della frazione; poi bisogna sommare il risultato ottenuto con numeratore nella frazione, ottenendo così il nuovo numeratore; il nuovo denominatore sarà invece quello della frazione.
Sottrazione di frazioni
1) Sottrazione di frazioni con stesso denominatore:
Si sottraggono i numeratori e si conservano i denominatori
2) Sottrazione di frazioni con denominatori diversi:
Si applica la trasformazione di più frazioni in frazioni equivalenti con lo stesso denominatore e poi si sottrae come nel caso 1.
3) Sottrazione di un numero intero con una frazione:
Si deve moltiplicare il numero intero per il denominatore della frazione; poi bisogna sottrarre al risultato ottenuto il numeratore nella frazione, ottenendo così il nuovo numeratore; il nuovo denominatore sarà invece quello della frazione.
Moltiplicazione di frazioni
Per moltiplicare due o più frazioni si moltiplicano tra loro i numeratori e i denominatori.
Se è possibile, si possono semplificare le frazioni a croce prima di eseguire la moltiplicazione.
Divisione di frazioni
Per dividere due frazioni, si moltiplica la prima per l’inversa della seconda.
Dopo aver invertito, si può semplificare come nella moltiplicazione .
Elevamento a potenza
Per eseguire tale operazione è necessario elevare a potenza sia il numeratore che il denominatore.
NOTE SULLE FRAZIONI
E’ buona norma tener presenti le seguenti note:
Se n ¹ 0 allora 0 : n = 0 n : 0 è impossibile 0 : 0 è indeterminato
Espressioni con le frazioni
1. 
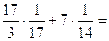
2. 
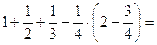
3. 
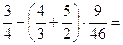
4. 
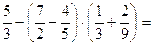
5. 
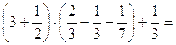
6. 
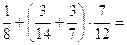
7. 
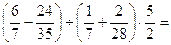
8. 
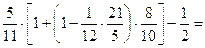
9. 
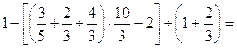
10. 
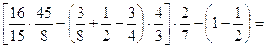
11. 
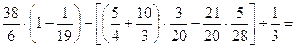
12. 
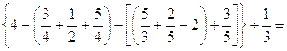
13. 
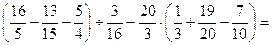
14. 
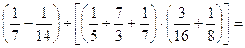
15. 
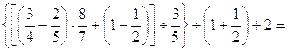
16. 
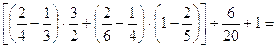
17. 
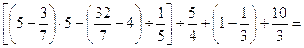
18. 
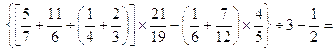
19. 
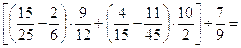
20. 
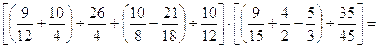
21. 
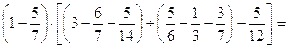
22. 
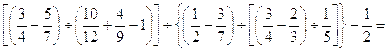
23. 
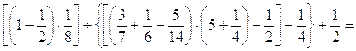
24. 
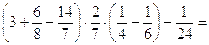
25. 
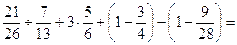
26. 
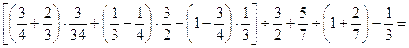
27. 
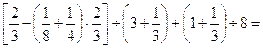
28. 
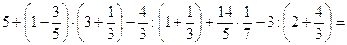
29. 
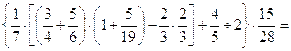
30. 
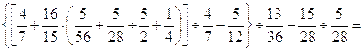
31. 
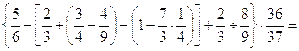
32. 
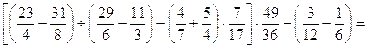
33. 
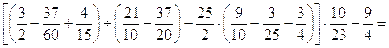
34. 
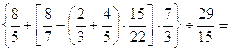
35. 
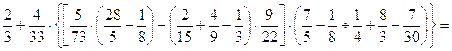
36. 
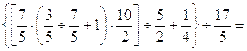
37. 
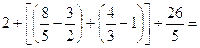
PROBLEMI SULLE FRAZIONI
- Su 500 bambini intervistati in una città i 3/10 hanno detto di essere costretti a giocare sempre in casa, i 2/5 nei cortili e i 3/25 in terreni aperti. I rimanenti giocano nei parchi e nei giardini pubblici. Quanti sono questi ultimi?
- In un frutteto sono stati raccolti 136 kg di mele corrispondenti ai 2/7 dell’intero raccolto. Se tutto il raccolto viene messo in cassette che contengono 14 kg di mele ciascuna, quante cassette vengono riempite?
- 2/7 dei giocattoli che ci sono in un negozio sono meccanici; si tratta di 20 macchinine, 12 soldatini, 18 piccole moto, 15 robot e 5 bambole. Quanti sono i giocattoli non meccanici?
- Un automobilista deve percorrere un tragitto di 2400 km. Il primo giorno ne percorre i 5/24 e il secondo 1/6. Quanti chilometri ha percorso il primo e il secondo giorno? Quanti ne restano da percorrere?
Fonte: http://www.liceocrespi.it/Accoglienza/Frazioni%20numeriche.doc
Autore del testo: non indicato nel documento di origine
Frazioni numeriche
Frazioni numeriche
Disclaimer
Questo sito non rappresenta una testata giornalistica e viene aggiornato senza alcuna periodicità, esclusivamente sulla base della disponibilità del materiale, pertanto non è un prodotto editoriale sottoposto alla disciplina di cui all'art. 1, comma III della Legge n. 62 del 7.03.2001. I riassunti , gli appunti i testi e le citazioni contenuti nel nostro sito sono messi a disposizione gratuitamente a studenti, ricercatori, professori, tecnici con scopi illustrativi didattici e scientifici con il concetto del fair use e con obiettivo del rispetto della direttiva europea 2001/29/CE e della legge n. 633 art. 70 e dlg 68. Il sito è curato e coordinato dall’autore al solo scopo informativo e didattico. Pur ritenendo le fonti utilizzate affidabili, l'autore di questo sito non garantisce l'accuratezza e l'integrità delle informazioni contenute e pertanto declina ogni responsabilità per eventuali problemi o danni causati da errori o omissioni, nel caso tali errori o omissioni risultino da negligenza, caso fortuito o altra causa. Tutti gli appunti, le citazioni i testi e le immagini , sono proprietà dei rispettivi autori o case di produzione che ne detengono i diritti, qualora gli aventi diritto si ritenessero danneggiati dall'inserimento in questo sito dei predetti files o fossero stati inavvertitamente inseriti immagini, informazioni, testi od altro materiale coperto da Copyright saranno immediatamente rimossi e/o ne saranno citate le fonti su semplice segnalazione all' indirizzo e-mail indicato nella pagina contatti .
Gli obiettivi di questo sito sono il progresso delle scienze e delle arti utili in quanto pensiamo che siano molto importanti per il nostro paese i benefici sociali e culturali della libera diffusione di informazioni utili. Tutte le informazioni e le immagini contenute in questo sito vengono qui utilizzate esclusivamente a scopi didattici, conoscitivi e divulgativi. Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione). In questo sito abbiamo fatto ogni sforzo per garantire l'accuratezza dei tools, calcolatori e delle informazioni, non possiamo dare una garanzia o essere ritenuti responsabili per eventuali errori che sono stati fatti, i testi utilizzati sono stati prelevati da siti che li hanno messi a disposizione gratuitamente per farli conoscere nel web con scopi didattici. Se trovate un errore su questo sito o se trovate un testo o tool che possa violare le leggi vigenti in materia di diritti di autore, comunicatecelo via e-mail e noi provvederemo tempestivamente a rimuoverlo.
Frazioni numeriche
Designed by Larapedia.com 1998 -2011