La quadratura del cerchio

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

La quadratura del cerchio

LA QUADRATURA DEL CERCHIO

PREMESSA

“Quadrare il cerchio” significa individuare un quadrato che abbia la stessa area di un cerchio assegnato di raggio r. Per essere più precisi significa calcolare la misura del lato di tale quadrato a partire dall’area del cerchio.

In modo del tutto analogo, “rettificare una circonferenza” significa individuare un quadrato che abbia lo stesso perimetro della circonferenza di raggio r. Per essere più precisi significa calcolare, ancora una volta, la misura del lato di tale quadrato a partire dal perimetro della circonferenza.

Come si vede, la prima affermazione riguarda le aree e la seconda i perimetri.

Entrando subito in argomento, bisogna ricordare che, fin dai tempi più remoti, si era scoperto che il rapporto tra le aree dei cerchi e il quadrato dei loro raggi (al pari che il rapporto di qualsiasi circonferenza col suo diametro) dava sempre come risultato una costante (che molti secoli dopo verrà battezzata con il simbolo di “pi greco”). Cioè:

Oggi è noto che tale costante è un numero irrazionale, quindi un numero decimale illimitato e non periodico, cioè un numero inconoscibile nella sua interezza.

Poiché il lato del quadrato sopraindicato dipende, come vedremo, da pi greco, tale lato sarà a sua volta inconoscibile.

La così detta “quadratura del cerchio” è perciò un progetto impossibile. Da ciò deriva il popolare e colloquiale modo di dire “vuoi quadrare il cerchio” riferito appunto a chi pretende di compiere un’operazione impossibile.

Questo almeno dal punto di vista puramente geometrico e aritmetico (il patrimonio della cultura greca). Vedremo più avanti come con l’avvento dell’Analisi Infinitesimale nel XVII secolo (e il relativo “passaggio al limite”) tale sogno riuscirà a realizzarsi, almeno nel senso del calcolo numerico.

Tuttavia non è per nulla secondario annotare che tale calcolo di limite (il quale con Leibniz e Newton ha reso possibile la realizzazione dell’antico sogno) altro non è se non la continuazione degli studi dei greci e, in particolare, di quell’Archimede che, a Siracusa nel 220 a.C., aveva concepito il “metodo di esaustione”, vero e proprio precursore del concetto di limite e del moderno calcolo integrale.

IL PROBLEMA DELLA QUADRATURA DEL CERCHIO

Essendo l’area del cerchio A= πr ², il quadrato di lato l e di area l ² dovrà essere tale che:

πr ²= l ² ma allora sarà:

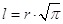
dove è ovvio che, essendo π inconoscibile, sarà inconoscibile anche la sua radice quadrata.

SUL VALORE DELLA COSTANTE

Appare evidente di come il problema della quadratura del cerchio rimandi alla conoscenza di π.

Sul valore e sul significato di questa costante l’umanità ha indagato, cercato e calcolato fin dai tempi più remoti. E ciò non per pura speculazione astratta, quanto perché essa entra in gioco tutte le volte che mettiamo in relazione linee circolari con linee rette oppure, tanto per spostarci subito nel campo delle applicazioni fisiche o tecniche, quando per esempio si debba confrontare, in un motore a scoppio, il movimento lineare del suo pistone con il movimento circolare dell’albero motore.

Dal punto di vista strettamente storico la prima valutazione di π si riscontra nella Bibbia (Libro dei Re I,7,23), laddove, parlando di un recipiente circolare utilizzato per i lavaggi sacri, si stima che il rapporto tra la circonferenza e il suo diametro sia π = 3.

I greci, come vedremo, arriveranno a fare molto di più individuando, sia pur dopo molti tentativi errati o imprecisi, otto decimali esatti dopo la virgola (oggi siamo giunti a conoscerne 5.000 miliardi!).

Ma per i greci sussisteva anche un altro problema che era quello di considerare le figure geometriche comprensibili e gestibili solo se si è in grado di trasformare una figura nell’altra con l’esclusivo uso della riga e del compasso.

Questo portò i greci a ripetuti tentativi tra i quali vogliamo illustrare il seguente e celebre metodo geometrico che permise loro di ottenere un valore di π esatto fino alla quarta cifra decimale (vale a dire approssimato a meno di un decimillesimo, cioè, come usa dirsi in gergo aritmetico, approssimato a meno di 10 ^{– 4}):

C A 3r D

30°

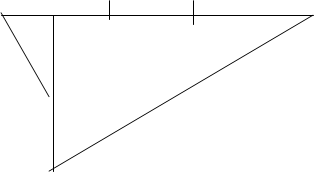
dopo aver costruito la figura con l’angolo COA = 30° e con CD = 3r, ci proponiamo di far vedere

che il segmento BD è metà della circonferenza.

Con la geometria elementare o con la trigonometria si ha:

inoltre

successivamente, applicando il Teorema di Pitagora al triangolo ADB:

i greci, naturalmente, sapevano calcolare le radici quadrate, e ciò permise di calcolare:

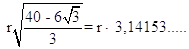
(1)

Poiché abbiamo supposto che 2·BD sia lungo come la circonferenza, si avrà:

Se ora confrontiamo il valore trovato con quello ottenibile con una moderna calcolatrice:

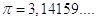
notiamo che, mentre le prime quattro cifre decimali sono esatte, la quinta cifra dei greci è in difetto di 6 centomillesimi (9 – 3 = 6).

Il che dimostra che 2·BD non è esattamente la circonferenza. In questo caso si dice che il risultato trovato è approssimato per difetto a meno di un decimillesimo, cioè a meno di 10 ^{– 4}.

Col passare dei secoli altri tentativi di natura geometrica furono fatti senza tuttavia miglioramenti significativi (si arrivò, appunto, fino all’ottava cifra decimale).

Al metodo di esaustione concepito da Archimede (220 a.C.) vorremmo lasciare uno spazio a parte, visto che, se è pur vero che si basa ancora su costruzioni geometriche, è anche vero che sembra poi sconfinare in un promettente calcolo numerico.

Il metodo è il seguente: data una circonferenza, disegniamo un quadrato iscritto e uno circoscritto a tale circonferenza. Supponiamo note le aree dei due quadrati.

Ora aumentiamo il numero dei lati di tali quadrati, ottenendo progressivamente pentagoni, esagoni, eptagoni, ottagoni e via di seguito. Ciò che è evidente è che, all’aumentare del numero dei lati, mentre l’area dei poligoni iscritti aumenta quella dei poligoni circoscritti diminuisce. Tali aree sono ovviamente facilmente calcolabili, essendo sempre scomponibili in triangoli isosceli.

Aumentando indefinitamente il numero dei lati dei poligoni, è del tutto intuibile che l’area del cerchio rimarrà “schiacciata” in mezzo.

La quadratura, geometricamente parlando, appare perfettamente riuscita!

Si capisce che, per avere un calcolo perfetto, il numero dei lati dovrebbe essere infinito e questo fa vedere in quale modo la proposta archimedea sia una vera e propria anticipazione dell’Analisi Infinitesimale di duemila anni dopo.

Tra i tanti tentativi basati sul metodo di esaustione, citiamo, a solo titolo di esempio, quello di Jamshid al-Kashi in Persia che nel 1420 d.C. individuò 9 cifre decimali corrette utilizzando poligoni di 3 × 2 ²⁸lati (un numero davvero spaventoso!).

Non sfugga quest’ultima data che abbiamo citato: mancano poco più di due secoli per il grande momento che cambierà la storia del pensiero. Infatti nel 1675, Leibniz in Germania e Newton in Inghilterra, non senza reciproche polemiche, annunciano al mondo il Limite, la Derivata, l’Integrale e, di seguito, lo Sviluppo in serie. Per inciso, pochi anni dopo, Leibniz costruirà anche una calcolatrice meccanica capace di compiere le quattro operazioni aritmetiche fondamentali.

Il calcolo di π adesso appare possibile, almeno in linea di principio. Naturalmente, abbiamo il dovere di spiegare cosa si debba intendere con “almeno in linea di principio”.

Per fare questo dobbiamo introdurre la nozione di “Sviluppo in serie”. Siamo infatti consapevoli che i nostri studenti dell’ultimo anno, mentre sono ben coscienti e preparati sul concetto di Limite, di Derivata e di Integrale, per quel che riguarda lo Sviluppo in serie ne sanno poco o niente (in attesa degli studi superiori).

Tuttavia, per quel che ci riguarda, è sufficiente conoscere che, tramite lo Sviluppo in Serie, una funzione matematica y = f(x) può essere sostituita dalla somma di più monomi, spesso prevedibili secondo criteri progressivi di facile costruzione o, nei casi più complessi, calcolabili con le derivate successive (Polinomio di Taylor).

Per esempio al posto della funzione,

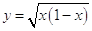
si può scrivere:

(2)

dove, come si vede, al secondo membro è presente un polinomio semplice somma di monomi algebrici.

I puntini lasciano intendere che al secondo membro si ha un’espressione approssimata.

Il secondo membro sarà tanto più preciso quanto più numerosi saranno i termini scritti verso destra. Ora siamo pronti per esporre quello che storicamente fu il primo esempio fatto da Isaac Newton.

Avvertiamo chi non si sentisse di seguirci nei calcoli di saltare, senza troppi svantaggi, direttamente a CONCLUSIONE.

In un sistema di assi cartesiani, sia data una circonferenza di raggio ½ e centro C(1/2;0), pertanto la sua equazione è x² + y²– x = 0, che, in forma esplicita e considerata solo positiva, è:

L’angolo indicato sia di 60°.

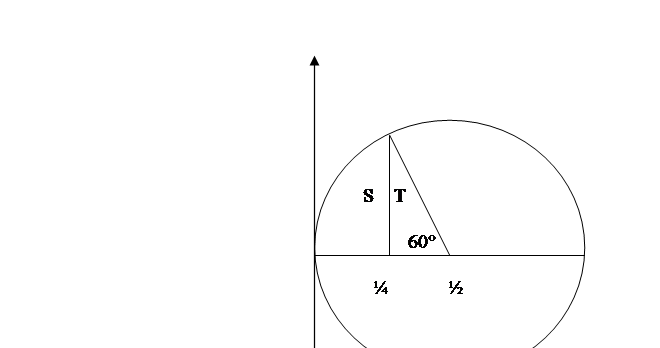
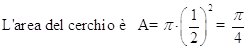
(3)

Utilizzando il calcolo integrale (come si vede un integrale razionale elementare sicuramente alla portata di qualunque principiante), si potrà scrivere:

dove abbiamo usato la sostituzione (2).

Tenendo conto della (3), potremo scrivere:

CONCLUSIONE:

(4)

Da questa espressione si prefiggiamo di calcolare il valore di π.

Il secondo membro è un normale integrale definito che sarà tanto più preciso quanto più numerosi saranno i termini che abbiamo scritto al posto dei puntini.

Con questo metodo Newton fu in grado di calcolare 16 cifre esatte di π, ma naturalmente, se avesse voluto, avrebbe potuto raggiungere un grado di precisione superiore soltanto aumentando il numero dei termini collocati al posto dei puntini.

La conoscenza di π così ottenuta consente dunque di “quadrare il cerchio” poiché permette di calcolare il lato del quadrato, di cui si diceva all’inizio, preciso quanto si desidera.

EPILOGO

Due considerazioni in chiusura.

La prima di natura culturale per segnalare che, facendo apparire l’Occidente come l’epicentro del mondo, abbiamo ingiustamente trascurato tutte quelle regioni del mondo nelle quali, parallelamente a noi, fiorivano e fecondavano, spesso in modo del tutto indipendente, analoghe o equivalenti scoperte matematiche: Cina, India e Arabia prime tra tutte.

La seconda per ammonire che non tutti i guai si concludono con π. Infatti non sarà sfuggito che nelle formule (1) e (2) figura la radice di 3, numero anch’esso irrazionale e perciò inconoscibile nella sua interezza.

Tuttavia, a differenza di π (che oltre che irrazionale è anche un numero trascendente*), per la radice di 3 disponiamo di un calcolo collaudato e sicuro (e fattibile anche da uno studente di seconda media), il quale consente di disporre del grado di precisione che si desidera volta per volta.

Ma è chiaro che, alla fine, anch’esso finisce col condizionare il valore di π.

* Dicesi trascendente un numero che non può esser soluzione di alcuna equazione di secondo grado

a coefficienti razionali.

Non sorprenda pertanto, quando si parla di quadratura del cerchio, sentir raccontare della “Duplicazione del cubo” (dove cerchi e curve sono per la verità del tutto assenti), in particolar modo associando tale questione con la leggenda dell’oracolo di Delo.

Semplificando, mettiamo in evidenza che la duplicazione del cubo, resasi necessaria per ingraziarsi gli dei, passava necessariamente per la radice cubica di 2 e quindi riproponeva la sua inconoscibilità.

Con la differenza non lieve, ma sostanziale, che mentre i decimali della radice cubica di 2 sono disponibili per chiunque, il valore di π passa per le forche caudine cui abbiamo accennato.

Una considerazione finale: abbiamo già detto che Leibniz (correva l’anno 1673) costruì la prima calcolatrice meccanica.

E siamo ancora qui a chiederci fino a che punto il poliedrico scienziato-filosofo tedesco, già accusato di aver “scopiazzato” da Newton Derivate e Integrali, si possa essere “ispirato” alle “pascaline” che il giovane Pascal aveva concepito e costruito tramite ruote di legno dentate più di cent’anni prima.

Una visita al Palais de la Decouverte di Parigi o anche, in tono minore, al Museo delle Scienze di Milano basterebbe per rendersi conto, ammirando le affascinanti “pascaline”, come ad esse manchi solo la corrente elettrica per entrare a pieno titolo nell’era moderna.

Si tratta in ogni caso di un passaggio chiave nella storia dell’umanità, nella quale i progressi della conoscenza sono sempre strettamente connessi alla precisione dei sistemi di misura.

Servirà il genio di James Maxwell che, a metà dell’ottocento, conclude (sarebbe meglio dire “apre”) la grande avventura scientifica della scoperta dell’energia elettrica.

E successivamente il genio di Alan Turing che, un secolo dopo, darà vita alla prima Intelligenza Artificiale.

Con l’avvento dei calcolatori la frontiera viene varcata!

L’inconoscibile π, questo mistero dell’irrazionale (ma anche del trascendente), può svelare ora “quasi” tutti i suoi segreti!

Anche se poi, alla fine, ci dovremo arrendere perdendoci tra i suoi orizzonti lontani.

Come accade negli ultimi versi della Divina Commedia, quando Dante paragona alla quadratura del cerchio il suo fallito sforzo di cogliere l’immagine di Dio.

Qual è ‘l geomètra che tutto s’affige

per misurar lo cerchio e non ritrova,

pensando quel principio ond’elli indige,

tal era io a quella vista nova:

veder volea come si convenne

l’imago al cerchio e come vi s’indova;

P.S. Naturalmente a molti verrà da chiedersi quale sia il senso di una ricerca così esasperata sui decimali di π.

E’ la stessa domanda che taluni si pongono sulle ossessioni con cui i matematici talvolta indagano, per esempio, sui numeri primi o sulle stupefacenti meraviglie della sezione aurea.

Domande tanto più attuali in questi anni, quanto più si pensi che siamo quotidianamente inondati da messaggi internet nei quali ricorrono spettacolari simmetrie tra numeri o sorprendenti legami tra grandezze geometriche (spesso accompagnate da gradevoli commenti musicali).

Ovvio che sia difficile rispondere in due parole. Ma ci si può provare indicando che quando la vostra carta di credito (che per inciso rispetta i rapporti aurei tra base e altezza) striscia per autorizzare le vostre operazioni bancarie utilizza un sistema di sicurezza che analizza, in quella frazione di secondo, ben centomila numeri primi.

Oppure, riferendosi a π, è suggestivo indicare che nel momento in cui si voglia valutare la potenza di un computer appena costruito, il metodo comunemente usato sul nostro pianeta Terra è quello di chiedergli quanti decimali di π è in grado di sfornare.

Tanto per fare due banalissimi esempi.

Ma, al di là delle ricadute nel mondo e nella vita, vale sempre la pena ricordare che tali ricerche, anche quando non conducano ad applicazioni immediate, sono sovente feconde e ricche di scoperte collaterali.

Senza le quali (è possibile affermarlo con sufficiente grado di certezza) la conoscenza umana non sarebbe giunta fin dove è giunta.

Fonte: http://www.sparvierosecondo.it/LA%20QUADRATURA%20DEL%20CERCHIO.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : La quadratura del cerchio tipo file : doc

La quadratura del cerchio