trasformazioni geometriche nel piano

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

trasformazioni geometriche nel piano

TRASFORMAZIONI DEL PIANO

In geometria si definisce trasformazione geometrica piana una corrispondenza biunivoca del piano con sé stesso che conserva qualche proprietà geometrica del piano. Si può anche definire come una funzione biiettiva del piano in sé.

Nello studio di una trasformazione piana risulta particolarmente utile la conoscenza degli eventuali punti o rette che non vengono modificati. Un tale punto viene chiamato punto unito della trasformazione, la retta invece viene chiamata retta unita.

Isometrie piane

Le isometrie sono trasformazioni del piano reale che conservano la distanza tra punti.

Le isometrie del piano si possono classificare in:

traslazioni,
rotazioni (di cui fanno parte le simmetrie centrali),
simmetrie assiali,
glissosimmetrie. (di cui non ci occuperemo)

Trasformazioni piane non isometriche

Ci occuperemo solo di tre trasformazioni non isometriche:

omotetia (conserva gli angoli e i rapporti tra le distanze),
similitudine (conserva gli angoli e i rapporti tra le distanze),
affinità (conserva il parallelismo tra rette e la congruenza tra segmenti).

Possiamo affermare che le isometrie sono particolari similitudini e che queste sono particolari affinità.

Vediamo ora l’equazione delle varie trasformazioni a partire dalle isometrie:

Le isometrie si dividono in isometrie dirette (conservano il senso di rotazione dei punti) o indirette (non conservano il senso di rotazione), in particolare sono isometrie dirette la traslazione e la rotazione, sono inverse la simmetria e la glissosimmetria.

Traslazione

una traslazione è una isometria che sposta tutti i punti del piano di una distanza fissa nella stessa direzione. La si può anche interpretare come addizione di un vettore costante ad ogni punto, o come spostamento dell'origine del sistema di coordinate. Se è un vettore fisso, la traslazione τ è definita dall'equazione:

Non ha punti uniti, ma ha infinite rette unite, tutte quelle che hanno la stessa direzione del vettore che individua la traslazione.

Rotazione

una rotazione è una isometria del piano che sposta gli oggetti in modo rigido ruotandoli di un angolo fisso attorno ad un punto detto centro di rotazione.

L’equazione di una rotazione di centro O e angoloè:

A volte può far comodo conoscere l’equazione inversa:

L’equazione di una rotazione di centro C(a,b) e angoloè:

Ha un solo punto unito (il centro di rotazione), in generale non ha rette unite.

Tra le rotazioni ha particolare importanza la simmetria centrale, ovvero la rotazione di centro e angolo di rotazione 180°, questa ha equazione:

La simmetria centrale è involutoria, ovvero coincide con la sua inversa e composta con se stessa da’ l’identità.

Ha un solo punto unito (il centro di rotazione) e infinite rette unite, tutte le rette passanti per il centro di rotazione.

Simmetria assiale

Nel piano euclideo, due punti A e A' si dicono simmetrici rispetto a una retta r (cui non appartengono) quando r è l'asse del segmento AA'. Il punto A' è il simmetrico di A rispetto ad r e viceversa.

La trasformazione che associa ad ogni punto A che non appartiene ad r il punto A' suo simmetrico, e ad ogni punto C in r associa il punto C stesso, è detta simmetria assiale di asse r nel piano considerato.

La simmetria assiale è involutoria, cioè coincide con la propria inversa e composta con se stessa dà l'identità. La sua equazione dipende dall’asse di simmetria:

asse orizzontale: y = l • asse verticale: x = l

asse obliquo: y = mx+q

(l’equazione della simmetria si ottiene risolvendo il seguente sistema in x’ e y’):

La simmetria assiale ha infiniti punti uniti (tutti i punti dell’asse di simmetria, si dice che l’asse è una retta luogo di punti uniti) e infinite rette unite, infatti, tutte le rette perpendicolari all’asse sono rette unite e anche l’asse è una retta unita.

Omotetia

Un'omotetia di centro A è una trasformazione del piano che dilata o contrae le distanze da A di tutti i punti secondo un fattore h, lasciando invariate le rette passanti per A che per questo si dicono unite. In altre parole, un qualsiasi punto P del piano viene spostato sulla retta uscente da A e passante per P, in modo che la sua distanza da A cambi secondo un fattore costante h. L'unico punto che corrisponde a se stesso e che per questo si dice unito è il punto A.

Il punto A è il centro, mentre h è il rapporto dell'omotetia. Questa trasformazione geometrica è anche chiamata con termini più familiari dilatazione, se h>1, contrazione se 0<h<1.

Se "h=1" si ottiene ovviamente l'identità ovvero la trasformazione nella quale ogni punto corrisponde a se stesso.

Se h è negativo il punto P viene spostato nel punto della semiretta opposta alla semiretta AP e avente come distanza da A quella di P moltiplicata per |h|. Notiamo quindi che un'omotetia di fattore -1 è la simmetria centrale di centro il punto A.

Una omotetia, oltre a moltiplicare tutte le distanze per | $h |$ , moltiplica tutte le aree per $h 2$ .

Mediante i vettori, l'omotetia di centro A e di rapporto h≠0 si definisce più correttamente come la trasformazione geometrica che porta ogni punto P nell'unico punto P' soluzione dell'equazione vettoriale:

L'omotetia si dice diretta o indiretta secondo che il corrispondente rapporto sia positivo o negativo (come trasformazione però è sempre diretta).

L'omotetia è una particolare similitudine, la sua equazione è:

θ: )

Similitudine

Si chiama similitudine piana una trasformazione che trasforma una circonferenza in una circonferenza. Si può dimostrare che una trasformazione è una similitudine se e soltanto se è costante il rapporto di due qualunque segmenti corrispondenti (rapporto di similitudine).

Una similitudine ha equazione σ:

Oppure più semplicemente σ₁:

In questo caso la similitudine σ₁ è una similitudine diretta, σ₂è invece una similitudine indiretta.

è il rapporto di similitudine ed è uguale al rapporto di due segmenti corrispondenti, il rapporto tra le aree invece è k².

Affinità

È la trasformazione piana lineare più generica, la sua equazione è

α:

in particolare se l’affinità è indiretta.

Nelle affinità è importante calcolare il rapporto di affinità . Se due figure si corrispondono nell’affinità α il rapporto fra le loro aree è proprio il rapporto di affinità k.

Punti corrispondenti in un’affinità

Data un’affinità di equazione a: a.

Curve corrispondenti in un’affinità

Data una curva del piano (es. ) occorre trovare l’affinità inversa,

ovvero ricavare dall’equazione di α x e y in funzione di x’ e y’ (nel nostro caso ) e svolgere i calcoli.

Punti Uniti

Per quanto riguarda tutti i tipi di affinità è importante calcolare punti uniti e rette unite. I punti uniti si ottengono semplicemente risolvendo il sistema:

Rette Unite

Siccome se una retta r è unita la sua corrispondente in a è r stessa, possiamo dire che anche la corrispondente di r in a stessa.

Riprendiamo come esempio la trasformazione a:

Prima di tutto occorre controllare se vi sono rette unite verticali, ovvero del tipo x = h. Andiamo quindi a sostituire a x, .

Poi controllo se ho rette unite oblique. Una retta obliqua ha equazione . Affinché questa sia una retta unita deve accadere che:

Che ha soluzione

Quindi ho un’altra retta unita .

Classificazione delle affinità

Data l’equazione di un’affinità α: , se h > 0 l’affinità è

diretta, se h < 0 l’affinità è indiretta.

Inoltre se 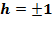. Per capire di quale isometria si tratta è sufficiente cercare i punti uniti infatti la traslazione non ne ha, la rotazione ne ha solo uno e la simmetria assiale ne ha infiniti (tutti i punti dell’asse).

Se abbiamo un’omotetia, una similitudine o un’affinità, riconoscibili facilmente perché le loro equazioni sono piuttosto differenti. Anche in questi casi occorre cercare punti uniti e rette unite.

Fonte: http://www.pascal.re.it/Documents/SpazioStudenti/materialeDidattico/scientifico%20moderno//Barozzi,%20Villa-4%20Sm%20A,B-Trasformazioni.doc

trasformazioni geometriche nel piano