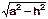Formule del volume

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Formule del volume

PARALLELEPIPEDO RETTANGOLO

diagonale di base

AREA base

perimetro di base

VOLUME

Diagonale

dimensione di base

Ö a2+b2

altezza del solido

Ab =a x b

pb= (a+b) x 2
pb= 2a + 2b

SL = pbxh

ST= 2Ab + SL

V = Ab x h

Ö a2+b2+h2

FORMULE INVERSE

a= (pb-2b) : 2
a = pb:2 - b

b= (pb-2a) : 2
b=pb:2 - a

h= SL : pb

Ab = (ST - SL) : 2

pb = SL : h

SL = ST - 2Ab

a =Ab : b

b= Ab : a

h= V : Ab

Ab = V : h

Ö d2- b2

Ö d2- a2

Ö D2- h2

Ö D2- d2

		PRISMA A BASE QUADRATA
l	h		AREA base	perimetro di base	SL	ST	VOLUME
lato di base	altezza del solido		Ab = l 2	pb= l x 4	SL = pb x h	ST= 2Ab + SL	V = Ab x h
FORMULE INVERSE
l = pb : 4	h= SL : pb		Ab = (ST - SL) : 2	pb = SL : h	SL = ST - 2Ab
l = ¶Ab	h= V : Ab		Ab = V : h

PIRAMIDE A BASE QUADRATA

apotema di base

a = apotema

sp= spigolo laterale

AREA base

perimetro di base

VOLUME

metà lato di base

lato di base

altezza del solido

a = teorema di
Pitagora
Ö h2 + (1/2 l ) 2

= teorema di
Pitagora
Ö a2 + (1/2 l ) 2

Ab = l 2

pb= lx4

SL = pb x a
2

ST= Ab + SL

V = Ab x h
3

FORMULE INVERSE

1/2 lato

o ß

l = pb : 4

h= teorema di Pitagora
Öa2 - (1/2 l ) 2

a = teorema di
Pitagora
Öspig lat2 - (1/2 l )2

Ab = ST - SL

pb = SL x 2
a

SL = ST - Ab

teorema di Pitagora Ý

l = ÖAb

h = V x 3
Ab

a = SL x 2
pb

Ab = V x 3
h

		CILINDRO
r	d	h	AREA base = cerchio	perimetro di base = circonferenza	SL	ST	VOLUME
raggio di base	diametro	altezza del solido	Ab = r 2p	pb= 2r p c = 2r p	SL = pbxh SL = 2r p xh	ST= 2Ab + SL	V = Ab x h V = r 2p x h
FORMULE INVERSE
r = d : 2	d = c : p	h= SL : pb h= SL : c	Ab = (ST - SL) : 2	pb = SL : h c = SL : h	SL = ST - 2Ab
r = c : 6,28 r= c : 2p	d = c : 3,14	h= V : Ab	Ab = V : h

			CONO
apotema di base	h	a	AREA base cerchio	perimetro di base	Sl	ST	VOLUME
raggio = 1/2 diametro	altezza del solido	apotema	Ab = r 2p	c= 2rp	Sl = c x a 2	ST= Ab + SL	V = Ab x h 3
Formule inverse
teorema di Pitagora	h= teorema di Pitagora	a = teorema di Pitagora	Ab = ST - Sl	c= Sl x 2 a	Sl = St - Ab
	h = V x 3 Ab	a = Sl x 2 c	Ab = V x 3 h
r= c : 2p r = c : 6,28

Fonte: http://utenti.romascuola.net/magnani/progetto%20matematica/formule%20solidi.doc

Formule del volume