Primo teorema di Euclide

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

Le informazioni di medicina e salute contenute nel sito sono di natura generale ed a scopo puramente divulgativo e per questo motivo non possono sostituire in alcun caso il consiglio di un medico (ovvero un soggetto abilitato legalmente alla professione).

Primo teorema di Euclide

I DUE TEOREMI DI EUCLIDE SUI TRIANGOLI RETTANGOLI

Il primo teorema di Euclide enuncia che: “in un triangolo rettangolo ciascun cateto è medio proporzionale tra l'ipotenusa e la proiezione dello stesso cateto sull'ipotenusa”. Con una diversa formulazione si può anche dire che: “in un triangolo rettangolo il quadrato costruito su uno qualsiasi dei cateti è equivalente al rettangolo che ha per dimensioni l'ipotenusa e la proiezione dello stesso cateto sull'ipotenusa” . Il secondo teorema dice che: “in un triangolo rettangolo l'altezza relativa all'ipotenusa è media proporzionale tra le proiezioni dei cateti sull'ipotenusa”. Oppure, usando una diversa versione: “in un triangolo rettangolo il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull'ipotenusa”.

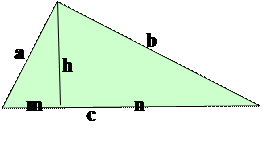
a = cateto minore

b = cateto maggiore

c = ipotenusa

m = proiezione del cateto a sull’ipotenusa

n = proiezione del cateto b sull’ipotenusa

h = altezza relativa all’ipotenusa

Primo Teorema:

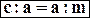
oppure

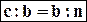
Secondo Teorema: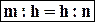

Fonte: http://www.maurolabarbera.it/Teoremi%20di%20Euclide(sito).doc

Sito web: http://www.maurolabarbera.it/

Autore del testo: non indicato nel documento di origine

Parola chiave google : Primo teorema di Euclide tipo file : doc

PRIMO TEOREMA DI EUCLIDE

In un triangolo rettangolo il quadrato costruito su ciascun cateto è equivalente al rettangolo che ha per lati l’ipotenusa e la proiezione del cateto stesso sull’ipotenusa

Basta osservare ad es. che i triangoli ABC e ABH sono simili, in quanto entrambi rettangoli e con l’angolo in B in comune

SECONDO TEOREMA DI EUCLIDE

In un triangolo rettangolo il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per lati le due proiezioni dei cateti sull’ipotenusa

Basta osservare che i triangoli AHC e ABH sono simili, in quanto entrambi rettangoli e con l’angolo in B congruente all’angolo A

I teoremi di Euclide in forma metrica

1° teorema di Euclide

Un cateto è medio proporzionale tra la sua proiezione sull’ipotenusa e l’ipotenusa stessa.

d : a = a : c

f : b = b : c

2° teorema di Euclide

L’altezza relativa all’ipotenusa è

media proporzionale tra le due proiezioni dei cateti sull’ipotenusa.

d : h = h : f

Fonte: estratto da http://www.liceoenriques.it/b1_dicembre__i__geometria.doc

Parola chiave google : Primo teorema di Euclide tipo file : doc

Primo teorema di Euclide