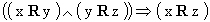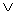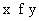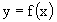Nozioni di teoria degli insiemi
Nozioni di teoria degli insiemi
I riassunti, le citazioni e i testi contenuti in questa pagina sono utilizzati per sole finalità illustrative didattiche e scientifiche e vengono forniti gratuitamente agli utenti.
Nozioni di teoria degli insiemi
Come si rappresentano gli insiemi?
Si specificano gli elementi dell'insieme |
Esempio:
A = 
|
Si usano i puntini di sospensione quando gli elementi espressamente indicati identifichino in modo naturale i successivi |
Esempio:
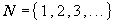
N rappresenta l'insieme di tutti i numeri naturali.
|
Si specifica la proprieta' P che identifica gli elementi dell'insieme: |
Esempio: si prenda l'insieme A come nell'esempio visto:
allora l'insieme
B = 
e' un sottoinsieme di A, i cui elementi sono caratterizzabili nel seguente modo:
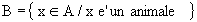
ATTENZIONE : Paradosso di Russel !!!
Dire che B rappresenta un insieme, qualsiasi sia la proposizione P, e' sbagliato.
E' classico l'esempio della proposizione 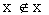 .
.
Dal supporre che 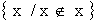 sia un insieme si ottiene il cosiddetto " Paradosso di Russel ".
sia un insieme si ottiene il cosiddetto " Paradosso di Russel ".
Sia A=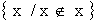 .
.
A e' l'insieme di tutti gli oggetti che non sono membri di se stessi.
A e' membro di se stesso?
|
Allora |
|
|
Allora |
Cosi', entrambe le risposte portano ad una contraddizione.
Questo esempio e' conosciuto come "Paradosso di Russel".
L'insieme vuoto non ha elementi:
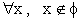
In una qualunque costruzione della teoria degli insiemi si dimostra che
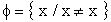 ( * )
( * )
e' un insieme.
L'insieme 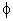 definito dalla ( * ) si dice "insieme vuoto".
definito dalla ( * ) si dice "insieme vuoto".
Sottoinsiemi
Dati due insiemi A e B diremo che A e' sottoinsieme di B e scriveremo
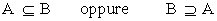
se ogni elemento di A è anche elemento di B
Operazioni tra insiemi
Insieme unione |
Si dice insieme unione di A e B (e si legge "A unione B") il seguente insieme: |
|
||
|
|
|
|
|
Si dice insieme intersezione di A e B (e si legge A intersezione B) il seguente insieme: |
|
||
|
|
|
|
|
A e B si dicono disgiunti se 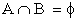
|
Si dice insieme differenza di A e B (e si legge A meno B) il seguente insieme: |
|
||
|
|
|
|
A - B e' l'insieme di tutti e soli gli elementi che appartengono ad A ma non a B. |
|
|
|
|
Se B e' un sottoinsieme di A si dice complementare di B rispetto ad A l'insieme A-B, che si indica anche con 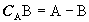
ATTENZIONE !
Si osservi che:
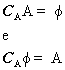
Proprietà delle operazioni fra insiemi
Proprieta' commutativa dell'unione e dell'intersezione |
Se A e B sono insiemi, si ha :
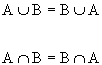
|
Se A, B, C sono insiemi si ha:
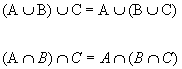
|
Se A, B, C sono insiemi si ha:
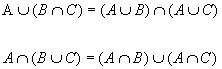
|
Se A e B sono sottoinsiemi di un insieme E si ha:
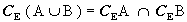
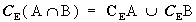
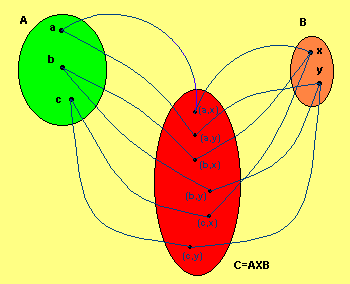
Prodotto cartesiano tra insiemi
Se A e B sono insiemi, si dice prodotto cartesiano di A per B il seguente insieme:
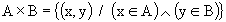
I due insiemi A e B si dicono fattori del prodotto cartesiano 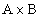
Prodotto cartesiano |
Dati due insiemi A e B, considerati nell’ordine, chiamiamo insieme prodotto di A per B o prodotto cartesiano di A per B ( che indichiamo con A x B) l’insieme di tutte le possibili coppie ordinate (a; b) aventi per prima componente un elemento aÎA e per seconda componente un elemento bÎB, in simboli: |
Prodotto cartesiano di n insiemi
Se 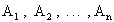 sono n insiemi, il prodotto cartesiano
sono n insiemi, il prodotto cartesiano
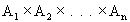
e' il seguente insieme:
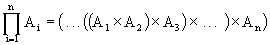
|
|
Proprietà del prodotto cartesiano(da cercare)
Relazioni tra insiemi
Se A e B sono insiemi si dice relazione fra A e B , e la si indica con 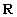 :
:
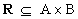
La proposizione 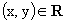
e si legge " x e' in relazione con y ".
Se A = B si dice che 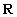 e' una relazione su A
e' una relazione su A
Relazione |
Dati due insiemi A e B, si chiama relazione di A in B ogni "proprietà", che si indica con R, tale che presi due elementi, xÎ A e yÎ B, la coppia (x,y) può:
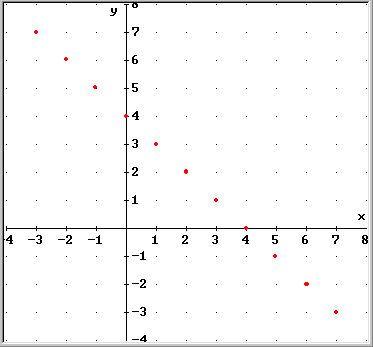
In generale una relazione individua un sottoinsieme del prodotto cartesiano AxB, ed ha quindi un grafico G Í .B x A
:ocifarg li
2 oipmesE
hce enoizaler al onacifirev e arugif al eneitto is ocifarg ni elodnatropir
|
Domini e condomini
Data una relazione 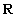 tra due insiemi A e B si dice
tra due insiemi A e B si dice
dominio di 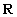 , il seguente sottoinsieme di A:
, il seguente sottoinsieme di A:
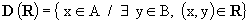
codominio di 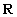 , il seguente sottoinsieme di B:
, il seguente sottoinsieme di B:
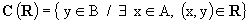
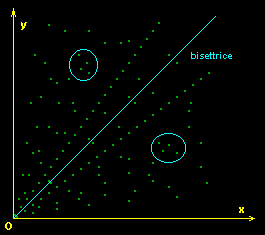
Relazione d’ordine
Una relazione 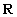 su un insieme A si dice relazione d'ordine se gode delle seguenti proprieta':
su un insieme A si dice relazione d'ordine se gode delle seguenti proprieta':
 proprieta' riflessiva
proprieta' riflessiva
 proprieta' antisimmetrica
proprieta' antisimmetrica
 proprieta' transitiva
proprieta' transitiva
Un insieme con una relazione d'ordine si dice insieme ordinato
|
|
Una relazione d'ordine 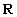 si dice relazione d'ordine totale se vale la seguente proprieta':
si dice relazione d'ordine totale se vale la seguente proprieta':
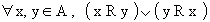 |
|
Un insieme con una relazione d'ordine totale si dice insieme totalmente ordinato.
Applicazioni fra insiemi
Dati due insiemi non vuoti A e B, diremo che una relazione fra A e B e' una applicazione da A a B, e la indicheremo con
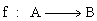
se ogni elemento di A e' in relazione con uno ed un solo elemento di B, cioe' se:
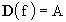 (si legge così: il dominio della funzione F è A)
(si legge così: il dominio della funzione F è A)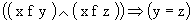
La proposizione |
|
si scrive anche |
|
Glossario
"Insieme", "elemento", "appartenenza" si assumono essere concetti primitivi, oggetti non definiti cui si assegna il significato comune e intuitivo
(tipo and)Il connettivo logico 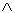 (et) si interpreta nel seguente modo:
(et) si interpreta nel seguente modo:
se P e Q sono proposizioni allora 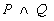 e' una proposizione, che risulta vera se e solo se sono vere contemporaneamente sia P che Q.
e' una proposizione, che risulta vera se e solo se sono vere contemporaneamente sia P che Q.
(tipo or)Il connettivo logico 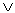 (vel) si interpreta nel seguente modo:
(vel) si interpreta nel seguente modo:
se P e Q sono proposizioni, 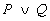 e' una proposizione, che risulta vera se e solo se :
e' una proposizione, che risulta vera se e solo se :
- o e' vera P
- o e' vera Q
- o sono vere entrambe
Sinonimi di "applicazione" : corrispondenza, funzione, mappa.
Se 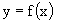 si dice che
si dice che
- y e' il corrispondente di x in f
- x e' l' argomento della f
fonte: http://www.alessandrobonini.it/download/matematica/Nozioni%20di%20teoria%20degli%20insiemi.doc
Autore: non indicato nel documento
Nozioni di teoria degli insiemi
Visita la nostra pagina principale
Nozioni di teoria degli insiemi
Termini d' uso e privacy


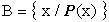
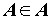 .
. 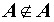 .
. 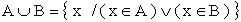
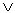
 Insieme intersezione
Insieme intersezione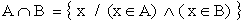
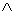
 Insiemi disgiunti
Insiemi disgiunti Insieme differenza
Insieme differenza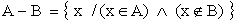
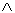
 Insieme complementare
Insieme complementare Proprieta' associativa dell'unione e dell'intersezione
Proprieta' associativa dell'unione e dell'intersezione
 Leggi di De Morgan
Leggi di De Morgan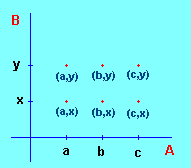
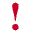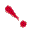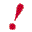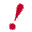
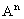 indica il prodotto cartesiano di A per se stesso n volte.
indica il prodotto cartesiano di A per se stesso n volte.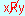
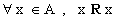
 proprieta' antisimmetrica
proprieta' antisimmetrica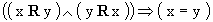
 proprieta' transitiva
proprieta' transitiva