Ottica di Euclide

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

L’Ottica di Euclide

Quest’opera comprende 62 proposizioni di ottica geometrica, riguardanti le forme e le dimensioni con cui gli oggetti illuminati appaiono all’occhio umano. I principi fondamentali della teoria sono elencati all’inizio, con il nome di premesse o definizioni o assiomi:

“1. I raggi emessi dall’occhio procedono per via diritta.
2. La figura compresa dai raggi visivi è un cono che ha il vertice all’occhio e la base al margine dell’oggetto.

Si vedono quegli oggetti cui arrivano i raggi visivi.
Non si vedono quegli oggetti ai quali i raggi visivi non arrivano.
Gli oggetti che si vedono sotto angoli maggiori, si giudicano maggiori.
Gli oggetti che si vedono sotto angoli minori, si giudicano minori.
Gli oggetti che si vedono sotto angoli eguali, si giudicano eguali.
Gli oggetti che si vedono con raggi più alti, si giudicano più alti.
Gli oggetti che si vedono con raggi più bassi, si giudicano più bassi.
Gli oggetti che si vedono con raggi diretti a destra, si giudicano alla destra.
Gli oggetti che si vedono con raggi diretti a sinistra, si giudicano alla sinistra.
Gli oggetti che si vedono con più angoli, si distinguono più chiaramente.
Tutti i raggi hanno la stessa velocità.
Non si possono vedere gli oggetti sotto qualunque angolo.”

Da queste premesse vengono dedotte le proposizioni, utilizzando semplici ragionamenti di geometria piana.

Gli enunciati sono per lo più semplici, ed enunciano fatti che risultano evidenti dall’esperienza, ma che Euclide vuole spiegare con rigore matematico:

Proposizione I

Un oggetto non può vedersi nella sua totalità d’un solo colpo d’occhio.

Proposizione II
Di oggetti eguali, differentemente distanti, i più vicini si distinguono più chiaramente.

Proposizione III
Per qualunque oggetto vi è una distanza determinata, oltrepassata la quale, esso non si vede più.
La comune origine di questi fenomeni risiede nel principio del cono visivo (che alcuni chiamano anche piramide), che è enunciato nella seconda premessa:

Il vertice è nell’occhio dell’osservatore, la base è data dai contorni dell’oggetto osservato.
Noi sappiamo che questo cono è formato dai raggi luminosi emessi dall’oggetto, e che è il prolungamento dello stesso cono al di là della pupilla a produrre l’immagine dell’oggetto sulla retina dell’osservatore. Da questo modello della visione si ricavano tutte le altre proprietà. Ad esempio, utilizzando le proprietà dei triangoli simili è immediato dedurre che tra due oggetti uguali posti a diversa distanza il più lontano apparirà più piccolo.

Ai tempi di Euclide, però, ancora non si sapeva che cosa avvenisse all’interno dell’occhio. Addirittura, la terza e la quarta premessa sembrano suggerire che, secondo Euclide, i raggi luminosi responsabili della visione dovessero provenire dall’occhio e non dall’oggetto osservato. Teone di Alessandria, nel suo commento all’opera, spiega che questa convinzione nasceva dal fatto che l’occhio, a differenza dell’orecchio e del naso, non possiede una cavità atta a ricevere corpi provenienti dall’esterno. Secondo un’altra interpretazione, i raggi citati da Euclide non sarebbero i raggi luminosi, ma le rette che delimitano il cono visivo.

In ogni caso, il modello di Euclide poteva basarsi esclusivamente sull’esterno dell’occhio. Così egli fa dipendere le dimensioni che l’oggetto assume per l’osservatore dall’angolo visivo, ossia dall’apertura del cono visivo:

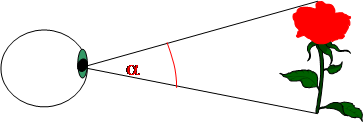
Euclide intuisce la relazione tra l’angolo a e le dimensioni della immagine e la enuncia nella quinta e nella sesta premessa.
Questa proprietà non è nient’altro che la più semplice delle leggi della prospettiva. Una proprietà ben più sofisticata è enunciata alla fine dell’opera: essa descrive il modo in cui un quadrato appare ad un osservatore che lo guardi obliquamente al piano del quadrato stesso.

Proposizione LXII
Se il raggio condotto dall’occhio sul punto d’intersezione dei diametri d’un quadrato non è perpendicolare sul piano di questo, né è eguale ad un mezzo diametro né fa angoli eguali con questi mezzi diametri, i diametri del quadrato appariranno ineguali.

I “diametri” del quadrato sono le sue diagonali: queste sono così chiamate perché coincidono con i diametri del cerchio circoscritto.

La prospettiva sarà oggetto di studio per i pittori a partire dal Rinascimento: vi si dedicarono con grande impegno, tra gli altri, Leonardo da Vinci, Leon Battista Alberti, Piero della Francesca ed Albrecht Dürer.

Nell’Ottica di Euclide i raggi si propagano sempre in linea retta: al fenomeno della riflessione egli dedicò un’opera a parte, la Catottrica,di cui ci è però pervenuta soltanto una versione apocrifa.

L’edizione dell’Ottica posseduta da Piero della Francesca

Curiosità sull’Ottica

Fonte: http://www.dm.uniba.it/ipertesto/euclide/ottica.doc

Autore del testo: non indicato nel documento di origine

Ottica di Euclide

Euclide di Alessandria, vissuto intorno al 300 a.C. é noto soprattutto per la sua più famosa opera “Gli Elementi”.
Nell’”Ottica”,uno dei primi trattati sulla prospettiva, Euclide pone alla base della teoria non la grandezza ma l’angolo sotto cui tale grandezza è vista.
Egli si propone di combattere il concetto secondo il quale le dimensioni di un oggetto erano quelle che apparivano alla vista, senza tenere alcun conto del rimpicciolimento dovuto alla prospettiva ossia alla geometria della visione diretta.
Il trattato è notevole per l’esposizione di una teoria “emissiva” della visione secondo la quale l’occhio emette raggi che attraversano lo spazio fino a giungere agli oggetti: per la prima volta è presente il concetto di cono visivo.
Leggiamo infatti nell’Ottica al secondo oros (affermazione):
la figura compresa dai raggi visivi è un cono che ha il vertice nell’occhio e la base al margine dell’oggetto visto.

Alcune proposizioni dall' Ottica di Euclide

Proposizione IV

Date due lunghezze su di una medesima retta, quelle che si vedono a distanza maggiore appaiono minori.

Proposizione V

Oggetti uguali ma inegualmente distanti [dall’occhio]appaiono ineguali e maggiore quello più vicino all’occhio.

Proposizione VI

Le rette parallele viste da lontano sembrano non equidistanti.

Proposizione VII

Oggetti uguali posti su di una stessa retta, ma tra loro distanti, appaiono disuguali.

Proposizione VIII

Segmenti uguali e paralleli, distanti dall’occhio in modo diseguale, sono visti sotto angoli che non sono proporzionali alle distanze relative.

Proposizione X

In piani sottostanti all’occhio, gli oggetti più distanti appaiono più alti.

Proposizione XI

In piani sovrastanti all’occhio, gli oggetti più distanti appaiono più bassi.
Notiamo che Euclide parla in termini di grandezze di angoli visivi e non di grandezza di immagini.
Ancora oggi l’Ottica è di estremo interesse per i suoi legami con la storia dell’arte, la pittura, la scenografia, l’astronomia e le varie tecnologie di rilevamento geografico.
I diversi scenari sono ‘mappabili’ con diverse geometrie: la geometria delle similitudini, dove domina l’invarianza del rapporto, la geometria proiettiva che governa il disegno prospettico e la geometria della sfera per rappresentare la volta celeste e i movimenti degli astri.
L’influenza dei risultati provati da Euclide è stata notevole sia nella tecnica che nel pensiero di studiosi e artisti nel periodo successivo al 300 a.C.: si può notare infatti la presenza di alcuni accorgimenti tecnici nella struttura degli edifici greci.
La visione scenografica della facciata del tempio greco ha una notevole rilevanza; le ricerche sull’ottica, unitamente alla pratica, hanno permesso di superare l’impressione di convergenza delle colonne che, altrimenti, apparirebbero appunto lievemente deformate alla visione. Per evitare il manifestarsi di tale aberrazione, molti edifici sono costruiti con opportune deformazioni opposte (descritte nel già citato De Architectura di Vitruvio).

Per vedere un'analisi grafica fare clic sull'immagine, con un modem a 56k il tempo necesario per scaricare l'animazione è di ca. 1 minuto
Molti autori nei secoli si occupano di ottica e prospettiva, ma assai diversi sono i punti di vista dai quali questa materia è trattata.
Tra gli studiosi ricordiamo Ipparco da Nicea (180-125 circa a.C.), astronomo operante ad Alessandria e a Rodi, considerato uno dei fondatori della trigonometria; dal punto di vista tecnico egli realizza la diottra, antenato del moderno teodolite ancora oggi usato dai geometri.
Agatarco in Atene, per la rappresentazione di una tragedia di Eschilo, curò la scena e Vitruvio ce ne lasciò notizia. Seguendo il suo esempio, Democrito ed Anassagora si occuparono del medesimo argomento, e cioè in quale modo le linee debbano corrispondere, in maniera naturale, alla visione degli occhi ed alla estensione dei raggi, fissato un certo punto come centro, affinché immagini determinate dell’apparenza rendano l’aspetto degli edifici nelle pitture sceniche
(Vitruvio De architectura trad. di U.Flores)

Esempi significativi compaiono nella pittura vascolare greca

Pittura vascolare greca del IV sec. a.C. Il tempietto è rappresentato in prospettiva parallela: prospetto anteriore e posteriore sono cioè collegati da linee oblique. Si tratta di primi tentativi dettati dalla intuizione e dalla osservazione che, comunque, portano alla costruzione di una struttura spaziale e di una tecnica di rappresentazione che probabilmente, in qualche misura, tiene conto delle esperienze dell’ottica scientifica del IV secolo a.C.

e negli affreschi di epoca romana dove frequentemente si trovano visioni di tipo prospettico-intuitivo per suggerire l’effetto di profondità, ma dallo studio di alcune rappresentazioni pare debole la padronanza della prospettiva e che il suo uso sia ancora a livello intuitivo e limitato all’utilizzo di chiaroscuro e ombre.

Paesaggi architettonici da affreschi di Pompei - (40-45 d.C.)

Villa dei Misteri - Pompei (affresco 90 a.C. circa)

Roma - pittura ellenistico romana (30 a.c.)
Importante fu il contributo di Vitruvio (ingegnere-architetto militare dell’età augustea) che, consapevole delle possibilità offerte dalla geometria alla risoluzione di problemi tecnico pratici ed in particolare alla rappresentazione di edifici, nel suo trattato De architectura definisce la scenografia come lo schizzo della facciata e dei lati in scorcio con la convergenza di tutte le linee del centro... e scrive "La geometria poi offre molti aiuti all’architettura, ed innanzitutto insegna l’uso della riga e del compasso, mediante i quali si possono disegnare con grande facilità nel piano piante di edifici, schizzi di livellamento e linee perpendicolari"
Dopo la fine dell’Impero Romano d’Occidente (476 d.C.) la teoria della prospettiva si è evoluta in modo molto lento. Ironizzando sulle convenzioni spaziali dell'arte medioevale, l'autore di questa vignetta fa esclamare al re, mentre il pranzo sta precipitando a terra: "E' tutta colpa di come disegnano questi maledetti tavoli"

Nei secoli immediatamente successivi alla caduta dell’Impero romano d’occidente (476 d.C.) la rappresentazione dello spazio si orientò verso modalità fortemente antiprospettiche.

La veduta antiprospettica fu considerata necessaria per stabilire una sorta di naturalità visiva, nella quale tutte le figure, ugualmente collocate in un piano, potessero assumere lo stesso grado di importanza, rispetto ad una dimensione concettuale. La presenza del fondo oro, oltre che avere una valenza simbolica, rivestiva un preciso ruolo nel contribuire ad appiattire le immagini, negando così la suddivisione tra luce ed ombra.