Lancio del peso

 

 

 

Lancio del peso

 

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

 

 

IL GETTO DEL PESO

 

Le specialità di lancio in atletica leggera sono 4 e possono essere classificate, sulla base delle caratteristiche della rincorsa, in due tipologie:

  1. lineari (PESO e GIAVELLOTTO);
  2. rotatori (DISCO e MARTELLO).

Ogni singola specialità assuma una denominazione differente da quella generica di lancio in considerazione dell’azione che l’arto superiore lanciante dell’atleta compie per scagliare l’attrezzo il più lontano possibile.
Abbiamo quindi le seguenti terminologie più corrette:
- GETTO DEL PESO: il movimento che si effettua è da arto superiore flesso (nella posizione di partenza) ad arto superiore disteso (nella posizione finale dopo il lancio).
- LANCIO DEL DISCO e LANCIO DEL MARTELLO: l’azione tecnica si compie mantenendo in ogni sua fase l’arto superiore lanciante sempre disteso.
- TIRO DEL GIAVELLOTTO: il movimento si esegue partendo con l’arto superiore lanciante disteso, per poi fletterlo all’indietro nella fase preparatoria di caricamento e ritornare ad arto disteso nella fase finale di rilascio.  
In tutti i lanci ha un ruolo fondamentale la combinazione forza-rapidità. L’efficacia del lancio è notevolmente incrementata dal coinvolgimento degli arti inferiori insieme a quelli superiori e la capacità motoria più importante per un lanciatore è rappresentata dalla forza esplosiva degli arti inferiori.    

Il getto del peso consiste nel lanciare, facendo uso di un solo braccio, una sfera metallica, di peso differente a seconda del sesso e dell’età dell’atleta (maschi 7,257 Kg. - femmine 4 Kg.; a livello scolastico: allievi maschili 5 Kg. -  juniores maschili 6 Kg. - allieve e juniores femminili 3 Kg.), il più lontano possibile senza uscire dai limiti di una pedana circolare del diametro interno di 2,135 m. Il peso deve cadere all’interno di un settore di lancio, davanti alla pedana, di 40° (ora, con il nuovo regolamento internazionale, è di 34,92°) con il vertice coincidente con il centro della pedana.   


Sopra è presentata la pianta regolare della pedana circolare con fermapiede rialzato a forma di arco nella parte anteriore utilizzata nelle gare di getto del peso.

 
IMPUGNATURA DEL PESO:

Il peso è appoggiato prevalentemente sulle tre dita centrali (indice, medio, anulare) della mano, che è flessa al polso . Il peso è sostenuto dalle prime due falangi delle dita medie, che sono leggermente allargate, e non poggia sul palmo della mano. Questo per permettere all’atleta evoluto di effettuare un’ulteriore ultima spinta sull’attrezzo, nella fase finale dell’azione di lancio, per effetto dell’estensione delle dita. Il pollice ed il mignolo fungono da supporto e rafforzano la presa sostenendo il peso ai lati.
L’attrezzo è appoggiato sul collo sotto l’angolo della mandibola, e in tale posizione deve rimanere fino al completamento dell’azione di lancio, nel momento in cui l’arto superiore inizia la fase di distensione.        

ANALISI DELLA TECNICA DI LANCIO RETTILINEA O DORSALE (vedi anche la fotocopia con la sequenza disegnata delle varie fasi del movimento):

 

La tecnica è stata introdotta dallo statunitense Parry O’Brien (perciò l’azione tecnica viene anche definita stile O’Brien) negli anni cinquanta e si basa su uno spostamento rettilineo all’indietro.

Le fasi del lancio sono quattro (l’analisi tecnica prende in considerazione un atleta con l’arto destro dominante, un sinistro eseguirà lo stesso gesto con il movimento opposto):

  1. Posizione di partenza.
  2. Traslocazione.
  3. Posizione di piazzamento finale.
  4. Finale di lancio.

 
POSIZIONE DI PARTENZA
L’atleta si pone in appoggio sul piede destro, nella parte posteriore della pedana, con le spalle (o il fianco sinistro) rivolte nelle direzione di lancio e con l’attrezzo in appoggio contro il collo (sopra la clavicola). L’arto superiore destro è flesso al gomito rivolto in basso mentre quello sinistro è leggermente flesso verso l’avanti-alto per stabilire l’equilibrio.

TRASLOCAZIONE
Dalla posizione sopra descritta l’atleta compie una flessione del busto in avanti ed un contemporaneo caricamento sulla gamba destra che si piega come fosse una molla mentre la gamba sinistra si eleva, si flette e si avvicina all’altra gamba. Il ginocchio sinistro è leggermente dietro il ginocchio destro. Il tronco si flette sulla coscia destra e l’atleta si “raccoglie” prima di spostarsi velocemente sulla pedana per esplodere nel lancio finale.
Avviene dunque la cosiddetta traslocazione sul diametro della pedana: l’atleta compie contemporaneamente una spinta della gamba destra mentre la gamba sinistra, che si era flessa, si distende rapidamente  all’indietro (calcio all’indietro) per aiutare e rendere più veloce il movimento dell’arto destro; infatti il corpo trasloca rapidamente per effetto della distensione dell’arto sinistro e di una energica spinta di quello destro (movimento simile ad un balzo).

POSIZIONE DI PIAZZAMENTO FINALE
Terminata la fase di traslocazione l’atleta si trova nella posizione di piazzamento finale. Il piede destro lascia il terreno radente al suolo e va a prendere contatto all’incirca sul centro della pedana, in appoggio sull’avampiede e quindi con il tallone sollevato, pressoché contemporaneamente a quello sinistro, che prende molto velocemente contatto alla base del fermapiede, davanti al quale si arresta.
Il tronco, durante la traslocazione, si è rialzato leggermente. Il peso del corpo deve essere sull’arto inferiore destro, le spalle e l’arto superiore sinistro mantengono il più possibile la posizione di partenza.

FINALE DI LANCIO
Il finale di lancio inizia con la spinta verso l’avanti-alto della gamba destra con dinamica frontalizzazione del bacino che sarà completata dall’azione di distensione e tenuta della gamba sinistra (azione di puntello). Contemporaneamente avviene l’entrata del petto e del braccio destro che, con il gomito in fuori inizia a distendersi e lanciare. Nella fase di avanzamento del busto il braccio sinistro compie un movimento verso l’alto-avanti. Nell’azione finale di lancio le spalle sono direzionate frontalmente verso il settore di lancio, l’arto superiore destro è in completa estensione e l’articolazione del polso resta rigida con il palmo della mano rivolto in avanti.
Abbandonato l’attrezzo, l’atleta, per evitare in seguito alla dinamicità dell’azione di uscire dalla pedana compiendo così un  lancio nullo, è costretto ad effettuare il “cambio”, che consiste nella sostituzione del piede sinistro con il piede destro nell’appoggio sul terreno.
E’ questa un’azione che segue naturalmente al lancio, se tutte le azioni precedenti sono state eseguite nel rispetto della tecnica.

Va peraltro precisato che tutte le azioni sopra descritte, presentate come fossero fasi a sé stanti e quasi staccate le une dalle altre, sono in realtà armoniosamente fuse nel dinamismo esecutivo del gesto, la cui durata è comunque brevissima, inferiore al secondo (6-7 decimi).                       

CENNI DI REGOLAMENTO TECNICO    

La misurazione del lancio: la misurazione di ciascun lancio deve essere fatta immediatamente dopo il lancio, dall’impronta più vicina alla pedana lasciata dalla caduta del peso alla parte interna del fermapiede, lungo una linea che va dall’impronta fatta dall’attrezzo al centro della pedana.  

- Il peso deve essere lanciato dalla spalla con una sola mano. Nel momento in cui l’atleta prende posizione in pedana per iniziare un lancio il peso deve essere in stretta prossimità del collo o del mento e la mano non deve essere abbassata da questa posizione durante l’azione di lancio. Il peso non deve essere portato dietro la linea delle spalle.

- Il lancio è nullo se il concorrente, dopo che è entrato in pedana ed ha cominciato ad eseguire un lancio, tocca con qualsiasi parte del corpo il terreno al di fuori della pedana circolare o la parte superiore del fermapiede o si libera scorrettamente dell’attrezzo durante l’esecuzione dell’azione tecnica di lancio.

- Perché il lancio sia valido il peso deve cadere completamente entro i margini interni del settore di caduta.

- Il concorrente non deve lasciare la pedana fino a che l’attrezzo non ha toccato il terreno. Lasciando la pedana, il primo contatto con il terreno all’esterno della pedana deve avvenire completamente dietro la linea bianca tracciata all’esterno della pedana e che passa idealmente per il centro della pedana stessa.     

 

Fonte: http://88.42.123.18/didattica/files/edfisica/4.doc

 

Autore del testo: non indicato nel documento di origine

 

 

Lancio del peso

 

LANCIO DEL PESO

 

                   Il peso è una forza e quindi dal punto di vista fisico è improprio parlare di lancio del peso, dal momento che, ovviamente, non ha senso lanciare una forza. Sarebbe pertanto più adeguato il temine di lancio della sfera, come si parla di lancio del martello e del giavellotto. Nel corso di fisica abbiamo esaminato i valori che permettono ad un satellite di essere messo in orbita. La prima velocità cosmica (7,9 km/sec) è quella che permette ad un satellite di acquisire un’orbita circolare attorno alla Terra. Al di sotto di questa velocità si hanno orbite ellittiche che intersecano il suolo terrestre. Evidentemente il lancio di un oggetto quale la sfera dell’atleta rientra in questa categoria. Pertanto, la traiettoria che viene descritta dal peso è un arco di ellisse. Si può però dimostrare nei calcoli che seguono che, se consideriamo   costante l’accelerazione di gravità nel breve dislivello di quota interessato, la traiettoria si può approssimare ad un arco di parabola.
Sia infatti  il valore della velocità al lancio,   b l’angolo formato dalla direzione iniziale con l’asse x, t il tempo, g l’accelerazione di gravità, allora le equazioni del moto scomposte lungo l’asse x e l’asse y saranno le seguenti:


 



                                              (1)
 
 
dovendo essere uniforme la componente del moto in asse x e uniformemente decelerata la componente lungo l’asse y.

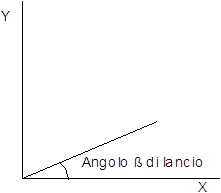
Calcolando il tempo nella prima equazione del sistema (1), cioè , e inserendolo nella seconda equazione, si ottiene la formula della traiettoria del lancio, cioè                    
   (2)   nella quale equazione si individua facilmente la natura di parabola.
Per calcolare la gittata, cioè la distanza massima alla quale viene scagliato l’attrezzo, occorre trovare le intersezioni con l’asse x, vale a dire si pone  y = 0 nella equazione  (2). Raccogliendo x si ottiene pertanto:

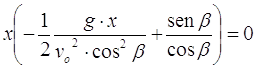
da cui otteniamo l’ovvia soluzione x = 0 e la soluzione

quantità che rappresenta quindi la gittata in funzione dell’angolo di lancio  .
Per valutare a quale angolo corrisponde la gittata massima si può fare ricorso allo studio della derivata prima o, più semplicemente, si studia la funzione
2senbcosb  che equivale anche alla sen2b.
Questa funzione non è altro che il grafico del seno in cui il periodo è però ristretto a p e quindi assumerà il valore massimo di 1 quando l’angolo 2b è uguale a p/2 e quindi, in conclusione, quando l’angolo di lancio b è uguale a p/4 cioè 45°.
Lanciare, stando fermi, cercando di proiettare l’attrezzo tra due corde tese ad una certa altezza. Con tale esercizio si impara a eseguire il lancio con il giusto angolo di uscita (l’angolo che il braccio forma con il terreno): quello ottimale è intorno ai 40°-42°.

In definitiva, ponendo quindi  b = p/4, la gittata massima diventa pertanto funzione della sola velocità iniziale   e della accelerazione di gravità g, cioè
gittata            (3)
Nella tabella seguente vengono riportati i valori della massima gittata considerando la velocità di lancio uguale a 15,05 m/sec, (54,18 km/h) sulla Terra e sulla Luna. Agli studenti il compito di reperire (o calcolare  (*)) le accelerazioni di gravità presenti su altri oggetti celesti e di determinare quindi la gittata relativa. La precedente velocità di lancio (trascurando ovviamente gli effetti dovuti all'attrito)  ha permesso allo statunitense Randy Barnes di stabilire il 25 maggio  1990 a Westwood il record del mondo con un lancio di 23.12 metri. Nell'ultimo decennio il livello delle misure nelle gare internazionali si è abbassato, forse per effetto degli sforzi anti-doping.

Con velocità di lancio di 15.05 m/sec la gittata sarebbe di:

 

accelerazione di gravità
(metri/secondo al quadrato)

Gittata  (metri)

     Sulla Terra

9.802

23.12

     Sulla Luna

1.27

178.5

     Su Mercurio

 

 

     Su Venere

 

 

     Su Marte

 

 

     Su Giove

 

 

     Sul  Sole

 

 

     Su Sirio

 

 

 

Grafico della gittata con velocità di lancio di 15.05 m/sec (valore approssimato del primatista del mondo) in funzione della accelerazione di gravità del corpo celeste.


Altre considerazioni.

  • Quale dovrebbe essere l’ipotetico raggio della Terra per permettere a Randy Barnes di mettere in orbita il peso con la sola forza delle sue braccia?

        
La prima velocità cosmica (velocità alla quale un oggetto lanciato parallelamente alla Terra entra in orbita circolare, ovviamente in assenza di attrito) è data dalla formula:

Se consideriamo quindi R come incognita, otteniamo la formula inversa:

 

                            .
Inserendo i valori numerici:


La Terra dovrebbe quindi avere un raggio  2500 volte più grande di quello del sole (che è di circa 700.000 km)!

 

  • Quale forza ha sviluppato Randy Barnes al momento del lancio?

Calcoliamo l’energia cinetica acquisita dal peso con una velocità iniziale di 15.05 m/sec:

Ipotizzando una spinta che avvenga per circa 70 centimetri, il lavoro compiuto sulla sfera sarà pertanto:

e quindi la forza sarà:
.

  • Quale influenza ha la forza d’attrito incontrata dal peso nella sua traiettoria attraverso l’aria?

La forza d’attrito viscoso per un oggetto circolare è data dalla formula:
la viscosità dell’aria e v la velocità dell’oggetto. Considerando una temperatura di 20°C, i calcoli porgono:

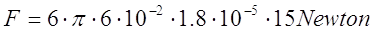
Per valutare il lavoro della forza di attrito dobbiamo calcolare il tragitto percorso durante il lancio, cioè la misura dell’arco di parabola descritto. Approssimando l’arco di parabola ad un triangolo isoscele di base 23 metri, occorre calcolare l’altezza per trovare con il teorema di Pitagora i due lati obliqui che sommati danno un valore approssimato per difetto della grandezza incognita. Per calcolare l’altezza impongo la conservazione dell’energia meccanica:

.       Inserendo i valori numerici otteniamo

e quindi un lato obliquo di circa 17 metri al quale corrisponde pertanto un arco approssimato di circa 34 metri.
Infine il lavoro della forza di attrito sarà pertanto
 

valore che, rispetto all’energia cinetica al lancio di 822 Joule rappresenta una percentuale soltanto dello 0.001%.
Si conclude che le forze di attrito sono del tutto trascurabili.

  • Quale è invece l’influenza della altitudine rispetto al livello del mare sulla gittata?

Consideriamo due località. Venezia e Cortina D’Ampezzo. Le accelerazioni di gravità sono rispettivamente 9.806 .
Utilizzando la formula (3) otteniamo pertanto una gittata rispettivamente di 22.945 m  e di 22.954 m. La variazione avviene solo sulla seconda cifra decimale, con una percentuale pertanto trascurabile dello 0.039%.

 

 



 
(*) Per il calcolo dell'accelerazione di gravità si può ricorrere alla formula

  dove M è la massa dell'astro ed R il suo raggio.

Fonte: http://www.liceocuriel.it/Facchin/lancio_del_peso.doc

 

Autore del testo: non indicato nel documento di origine

 

Lancio del peso

 

 

Visita la nostra pagina principale

 

Lancio del peso

 

Termini d' uso e privacy

 

 

 

Lancio del peso