Termodinamica

 

---

 

Termodinamica

 

La termodinamica è quella branca della fisica e della chimica (chimica fisica) che descrive le trasformazioni subite da un sistema in seguito a processi che coinvolgono la trasformazione di calore in lavoro e viceversa.

La termodinamica classica si basa sul concetto di sistema macroscopico, ovvero una porzione di materia fisicamente o concettualmente separata dall'ambiente esterno, che spesso per comodità si assume non perturbato dallo scambio di energia con il sistema. Lo stato di un sistema macroscopico che si trova all'equilibrio è specificato da grandezze dette variabili termodinamiche o di stato come la temperatura, la pressione, il volume, la composizione chimica. Tuttavia esiste una branca della termodinamica, denominata Termodinamica del non equilibrio che studia i processi termodinamici non-lineari caratterizzati dal mancato raggiungimento di condizioni di equilibrio stabile. Fu Sadi Carnot nel 1824 il primo a dimostrare che si può ottenere lavoro dallo scambio di calore tra due sorgenti a temperature differenti. Attraverso il teorema di Carnot e la macchina ideale di Carnot quantificò questo lavoro e introdusse il concetto di rendimento termodinamico.
Nel 1848 Lord Kelvin utilizzando la macchina di Carnot introdusse il concetto di temperatura termodinamica assoluta e a lui si deve un enunciato del secondo principio della termodinamica. Nel 1850 Joule dimostra l'uguaglianza delle due forme di energia (allora si credeva esistesse ancora il fluido calorico). A questo punto si era posto il problema che se era possibile ottenere calore dal lavoro in modo totale, non era possibile ottenere l'inverso. A questo risultato approda anche Clausius che nel 1855 introdusse la sua disuguaglianza per riconoscere i processi reversibili da quelli irreversibili e la funzione di stato entropia. Un sistema termodinamico è una porzione di spazio, separata dal resto dell’universo (cioè l’ambiente esterno) mediante una superficie di controllo (superficie reale o immaginaria, rigida o deformabile), sede di trasformazioni interne e scambi di materia o energia con l’ambiente esterno. I suddetti scambi possono avvenire sotto forma di calore o lavoro. Questi due concetti non sono delle proprietà intrinseche del sistema, ma sussistono nel momento in cui esso interagisce con l'ambiente, cioè scambia energia con l'esterno. Quindi un sistema non possiede calore o lavoro, bensì energia; ogni variazione di energia è poi esprimibile in termini di calore (se il passaggio di energia è dovuto ad una differenza di temperatura tra ambiente e sistema) e lavoro (per qualunque variazione energetica che non sia dovuta alla differenza di temperatura, come ad es. una forza meccanica che provochi uno spostamento, un trasferimento di energia elettrica o elastica).
I bordi dei sistemi termodinamici si possono classificare nel modo seguente:

• Sulla base dello scambio di calore in:
• Bordi adiabatici, se non consentono lo scambio di calore;
• Bordi diatermani, se invece lo consentono;

• Sulla base dello scambio di lavoro in:
• Bordi rigidi, se non consentono lo scambio di lavoro;
• Bordi flessibili, se invece lo consentono;

• Sulla base dello scambio di materia in:
• Bordi permeabili, se consentono il passaggio di ogni specie chimica
• Bordi semipermeabili, se consentono il passaggio di alcune specie chimiche
• Bordi impermeabili, se invece non consentono il passaggio di alcuna specie chimica.

Si possono distinguere vari tipi di sistemi, in dipendenza dal modo di scambiare energia con l'esterno:

• sistemi isolati: non scambiano calore, materia, lavoro con l'esterno (bordi impermeabili, rigidi e adiabatici);
• sistemi chiusi: scambiano energia (calore, lavoro), ma non materia con l'esterno. Quando un sistema scambia calore, lavoro o entrambi, lo si può classificare in base alle proprietà al bordo che sarà:
• impermeabile
• rigido o flessibile
• adiabatico o diatermano
• sistemi aperti: permettono scambio di energia e materia con l'esterno (cioè bordi permeabili o semipermeabili, diatermi e flessibili).

Coordinate termodinamiche
Le proprietà termodinamiche usate per descrivere un sistema sono dette coordinate termodinamiche. Dato un certo numero di coordinate, esse possono essere:

• indipendenti, se è possibile modificare il valore di ciascuna di esse senza determinare una variazione del valore delle altre;
• dipendenti, se variando il valore di una di esse anche le altre coordinate vengono modificate.

E' tipica della termodinamica la distinzione fra proprietà estensive ed intensive:

• estensive, se dipendono dalle dimensioni del sistema (ad es. massa, volume, capacità termica);
• intensive, se non dipendono dalle dimensioni del sistema (ad es. pressione e temperatura);
• specifiche: rapportando una proprietà estensiva con le dimensioni del sistema (tipicamente la massa, ma anche il numero di moli o il volume) si ottiene una proprietà intensiva che è detta la corrispondente specifica della proprietà estensiva corrispondente: volume specifico, densità ("massa specifica"), calore specifico...

Secondo un noto postulato di stato, date due proprietà intensive indipendenti, lo stato di un sistema semplice risulta completamente determinato.
Temperatura, volume, pressione e numero di moli sono i tipici esempi di coordinate termodinamiche.

Trasformazioni termodinamiche
Quando un sistema passa da uno stadio di equilibrio ad un altro, si dice che avviene una trasformazione termodinamica: si distingue tra trasformazioni reversibili, ovvero quelle trasformazioni che consentono di essere ripercorse in senso inverso (si ritorna precisamente al punto di partenza, ripercorrendo all'indietro gli stessi passi dell'andata), e trasformazioni irreversibili, ovvero quelle trasformazioni che, se ripercorse all'indietro, non faranno ritornare al punto iniziale, ma ad uno diverso. Perché una trasformazione sia reversibile è necessario che essa avvenga abbastanza lentamente da permettere al sistema di termalizzare (il sistema deve passare attraverso infiniti stati di equilibrio termodinamico). Le trasformazioni termodinamiche possono essere anche dei seguenti tipi:

• Isobare: se la pressione si mantiene costante;
• Isocore, se il volume si mantiene costante (e il lavoro scambiato tra sistema ed esterno è dunque nullo);
• Isoterme, se la temperatura si mantiene costante;
• Adiabatiche, se il calore totale scambiato è nullo;
• Isoentropiche, o adiabatiche reversibili, se la variazione di entropia è nulla;

I Principi della Termodinamica
I principi della termodinamica vennero enunciati nel corso del diciannovesimo secolo e regolano le trasformazioni termodinamiche, il loro procedere, i loro limiti. Sono dei veri e propri assiomi, non dimostrati e indimostrabili, fondati sull'esperienza, sui quali si fonda tutta la teoria che riguarda la termodinamica.
Si possono distinguere tre principi di base più un principio zero che definisce la temperatura, e che è implicito negli altri tre.

 

Principio Zero
Quando due sistemi interagenti sono in equilibrio termico, condividono alcune proprietà, che possono essere misurate dando loro un preciso valore numerico. In conseguenza, quando due sistemi sono in equilibrio termico con un terzo, sono in equilibrio tra loro e la proprietà condivisa è la temperatura. Il principio zero della termodinamica dice semplicemente che, se un corpo "A" è in equilibrio termico con un corpo "B" e "B" è in equilibrio termico con un corpo "C", "A" e "C" sono in equilibrio tra loro.
Tale principio spiega il fatto che due corpi a temperature diverse, tra cui si scambia del calore, (anche se questo concetto non è presente nel principio zero) finiscono per raggiungere la stessa temperatura. Nella formulazione cinetica della termodinamica, il principio zero rappresenta la tendenza a raggiungere un'energia cinetica media comune degli atomi e delle molecole dei corpi tra cui avviene scambio di calore: in media, come conseguenza degli urti delle particelle del corpo più caldo, mediamente più veloci, con le particelle del corpo più freddo, mediamente più lente, si avrà passaggio di energia dalle prime alle seconde, tendendo dunque ad uguagliare le temperature. L'efficienza dello scambio di energia determina i calori specifici dei materiali coinvolti.

 

Primo Principio
Quando un corpo viene posto a contatto con un altro corpo relativamente più freddo, avviene una trasformazione che porta a uno stato di equilibrio, in cui sono uguali le temperature dei due corpi. Per spiegare questo fenomeno, gli scienziati del diciottesimo secolo supposero che una sostanza, presente in maggior quantità nel corpo più caldo, passasse nel corpo più freddo. Questa sostanza ipotetica, detta calorico, era pensata come un fluido capace di muoversi attraverso la materia. Il primo principio della termodinamica invece identifica il calore come una forma di energia che può essere convertita in lavoro meccanico ed essere immagazzinata, ma che non è una sostanza materiale. È stato dimostrato sperimentalmente che il calore, misurato originariamente in calorie, e il lavoro o l'energia, misurati in joule, sono assolutamente equivalenti. Ogni caloria equivale a 4,186 joule. Il primo principio è dunque un principio di conservazione di energia. In ogni macchina termica una certa quantità di energia viene trasformata in lavoro: non può esistere nessuna macchina che produca lavoro senza consumare energia. Una simile macchina, se esistesse, produrrebbe infatti il cosiddetto moto perpetuo di prima specie. Il primo principio viene tradizionalmente enunciato come "In un sistema chiuso si ha che ΔU = Δq - Δw dove U è l'energia interna del sistema. Per Energia Interna si intende la somma delle energie cinetiche e di interazione delle diverse particelle di un sistema. Δq è il calore scambiato tra ambiente e sistema (positivo se fornito al sistema, negativo se invece ceduto dal sistema) e Δw il lavoro compiuto (positivo se compiuto dal sistema sull'ambiente, negativo invece se compiuto dall'ambiente sul sistema). La convenzione dei segni risente del legame con lo studio dei motori termici, nei quali il calore viene trasformato (parzialmente) in lavoro.
Formulazioni alternative ed equivalenti del primo principio sono:

• Per un sistema aperto, q-w=ΔE, ove per ΔE si intende la variazione di energia totale, che altro non è che la somma delle variazioni dell'energia interna , dell'energia cinetica e dell'energia potenziale possedute da quel sistema. Si vede che per un sistema chiuso le variazioni di energia cinetica e potenziale sono nulle per cui ci si riconduce alla relazione precedente.
• Per un ciclo termodinamico, q=w, dal momento che la variazione di energia totale è nulla, dovendo il sistema, al termine di ogni ciclo, ritornare nelle stesse condizioni di partenza.

Esempio del primo principio

 

Secondo Principio
Esistono diversi enunciati del secondo principio, tutti equivalenti, e ciascuna delle formulazioni ne mette in risalto un particolare aspetto. Esso afferma che è impossibile realizzare una macchina ciclica che abbia come unico risultato il trasferimento di calore da un corpo freddo a uno caldo o, equivalentemente, che è impossibile costruire una macchina ciclica che operi producendo lavoro a spese del calore sottratto a una sola sorgente. Quest'ultima limitazione nega la possibilità di realizzare il cosiddetto moto perpetuo di seconda specie. L’entropia  totale di un sistema isolato rimane invariata quando si svolge una trasformazione reversibile ed aumenta quando si svolge una trasformazione irreversibile.

Terzo Principio
È strettamente legato al secondo, e in alcuni casi è considerato come una conseguenza di quest'ultimo. Può essere enunciato dicendo che è impossibile raggiungere lo zero assoluto con un numero finito di trasformazioni e fornisce una precisa definizione della grandezza chiamata entropia. Esso afferma inoltre che l'entropia per un solido perfettamente cristallino, alla temperatura di 0 Kelvin è pari a 0. È facile spiegare questo enunciato tramite la termodinamica molecolare: un solido perfettamente cristallino è composto da un solo complessioma (sono tutti i modi di disporre le molecole, se le molecole sono tutte uguali indipendentemente da come sono disposte, macroscopicamente il cristallo è sempre uguale) e, trovandosi a 0 Kelvin, l'energia vibrazionale, traslazionale e rotazionale delle particelle che lo compongono è nulla, per cui, dalla legge di Bolzmann S = k ln(1) = 0 dove 1 sono i complessiomi (in questo caso uno solo).
 

Esempio di centrale termodinamica

Autore : Federica Pucinotti
Fonte: http://www.francescozumbo.it/zumbo/lavori-studenti/2008/cd-5g-2007-2008/lavori/pucinotti-Termodinamica-5g.rtf

 

Elementi di termodinamica chimica

 

Per descrivere in modo completo una reazione chimica non è sufficiente specificare il numero di moli di reagenti e prodotti di reazione che vi partecipano, ma è necessario descrivere anche i fenomeni energetici che l'accompagnano.
Tale descrizione è compito della termodinamica la quale permette di stabilire se una reazione chimica, scritta sulla carta, avvenga effettivamente in pratica.
In definitiva, attraverso lo studio delle trasformazioni energetiche che accompagnano sempre i fenomeni chimici, è possibile evidenziare i criteri di spontaneità delle reazioni e definire quali sono le condizioni termodinamiche affinché una reazione possa prodursi con la massima efficienza.

E' bene comunque ricordare che la termodinamica, occupandosi dei sistemi al punto di equilibrio, non è in grado di stabilire con che velocità una reazione avviene, ma solo se si produce e in che proporzione.

 

I sistemi termodinamici

Il termine sistema viene qui impiegato per descrivere la regione di spazio cui vengono limitate le nostre osservazioni. Tutto ciò che non appartiene al sistema è detto ambiente esterno o intorno del sistema. Il sistema più il suo intorno costituiscono complessivamente l’universo.
In linea di principio l’universo è costituito dall’universo propriamente detto, ma in pratica con questo termine si indica solo il sistema e quella parte dell’ambiente esterno con cui il sistema è a diretto contatto. Un sistema chimico è tipicamente composto dalle specie chimiche coinvolte nella reazione, mentre possiamo in pratica limitare l'ambiente esterno al recipiente che le contiene ed alla porzione di spazio circostante con cui il sistema intrattiene eventuali scambi di energia e/o di materia.

a) Si definiscono aperti i sistemi in grado di scambiare energia e materia con l'ambiente

b) Si definiscono chiusi i sistemi in grado di scambiare solo energia con l'ambiente

c) Si definiscono isolati i sistemi che non sono in grado di effettuare scambi con l'ambiente.

Come tutti i sistemi anche un sistema chimico possiede energia.

L'energia viene definita come la capacità di compiere lavoro o di trasferire calore.  Le unità di misura dell'energia sono quindi le stesse del lavoro e del calore.

Il calore (q) è l’energia termica trasferita tra il sistema e l’ambiente come risultato di differenze di temperatura.
Il lavoro (w) è l’energia trasferita tra il sistema e l’ambiente come risultato di una forza che opera su una distanza.
lavoro = forza x distanza
Le unità di misura maggiormente utilizzate in chimica sono il joule ( 1 J = Newton . metro = 1 kg . m2 . s-2) e la caloria (1 cal = energia necessaria per aumentare di 1°C la temperatura di 1 g d'acqua)

1 cal   =  4,184 J

Funzioni di stato e di percorso

Il valore assunto da una funzione  di  stato dipende solamente dalle condizioni in cui si  trova il sistema. È una caratteristica del sistema ed è indipendente dal modo in cui il sistema sia giunto in quelle condizioni. Sono funzioni di stato la temperatura, il volume, l'energia.

Il valore assunto da una funzione  di  percorso dipende dal percorso effettuatoedè una caratteristica del processo in esame. Sono funzioni di percorso il lavoro e il calore.

Ad esempio, l’altezza di una montagna è indipendente dal tragitto effettuato per arrivarci (l’altezza è una funzione di stato), mentre la lunghezza della strada dipende dal tragitto scelto per arrivare in cima (la lunghezza della strada e una funzione di percorso).

 

Energia interna (E)

L'energia posseduta da un sistema viene definita Energia interna E (spesso indicata anche come U).
L'energia interna di un sistema dipende esclusivamente dalla pressione, dalla temperatura, dal volume e dalla composizione chimica del sistema (tipo ed intensità delle interazioni tra particelle costituenti).
Per questo motivo l'energia interna è una funzione di stato. Il suo valore dipende cioè dallo stato termodinamico del sistema e non dal modo in cui tale condizione è stata raggiunta.
L'energia interna di 100 g di acqua a 25°c e 1 atm è la medesima che l'acqua sia stata ottenuta per condensazione di 100 g di vapore,  per reazione tra idrogeno ed ossigeno o per liquefazione di 100 g di ghiaccio.

Inoltre l'energia interna è una proprietà estensiva, è cioè proporzionale alla quantità di materia presente nel sistema.
100 g di acqua a 25°C e 1 atm possiedono un'energia interna doppia rispetto a 50 g di acqua nelle stesse condizioni termodinamiche.

L'energia interna di un sistema chimico è uguale alla somma dell'energia cinetica e dell'energia potenziale di tutte le molecole che formano il sistema.ed è associata ai moti traslatori, rotazionali, vibrazionali, elettronici e nucleari delle molecole, nonché alle interazioni interatomiche (legami intramolecolari) ed intermolecolari.

E = (Ec + Ep)

L’energia interna non include invece  l'energia cinetica e potenziale  associata al sistema nel suo complesso, ad esempio, se il sistema è in movimento o si trova in un campo gravitazionale o elettromagnetico.

L'energia cinetica di un corpo (Ec) è la capacità di compiere lavoro per effetto del suo moto. Essa dipende dalla massa m e dalla velocità v ed è pari a

Come abbiamo già anticipato, nel caso di un sistema di molecole, l'energia cinetica non è legata solo al movimento di traslazione, ma vi sono altri contributi connessi con i  moti di rotazione  e di vibrazione interna delle singole particelle.

La meccanica statistica dimostra che il valore medio dell'energia cinetica di un sistema di particelle è legato alla temperatura del sistema dalla relazione

E dunque l’energia cinetica di un sistema rappresenta la sua energia termica.

 

L'energia potenziale di un corpo è la sua capacità di compiere lavoro per effetto della sua posizione o dello stato in cui si trova.

Nel caso di un sistema di particelle l'energia potenziale viene comunemente definita energia chimica o di legame e presenta due componenti fondamentali. Una legata alla posizione reciproca delle molecole il cui valore dipende dalle forze attrattive intermolecolari (forze di Van der Waals), l'altra che dipende dalla posizione reciproca assunta dai protoni e dagli elettroni all'interno degli atomi e dalle interazioni elettromagnetiche che si producono tra le loro cariche e dunque dai legami chimici interatomici (covalente, ionico e metallico).

Quando effettuiamo un lavoro per allontanare due corpi che si attraggono (come accade tra molecole o tra elettroni e nuclei) allora l'energia potenziale del sistema aumenta e le forze di attrazione tra i corpi diminuiscono.

Al contrario quando lasciamo che due corpi che si attraggono si avvicinino l'energia potenziale diminuisce e le forze di attrazione tra i corpi aumentano.

Le reazioni chimiche sono sempre accompagnate da modificazioni energetiche in cui l'energia potenziale varia a causa delle modificazioni delle posizioni reciproche di atomi e di elettroni che si riassestano per occupare nuove posizioni nelle molecole dei prodotti di reazione.
In altre parole ogni reazione chimica avviene grazie alla rottura ed alla formazione di legami che modificano l'intensità delle forze all'interno delle molecole e tra le molecole, andando a modificare l'energia potenziale del sistema.

 

Se i nuovi legami che si formano sono più deboli il sistema presenta un'energia potenziale maggiore rispetto a quella che caratterizzava nel complesso le molecole dei reagenti.
Se al contrario i nuovi legami che si formano sono più forti il sistema presenta un'energia potenziale minore rispetto a quella che caratterizzava nel complesso le molecole dei reagenti.

Se il sistema è isolato e non può quindi scambiare energia con l'ambiente esterno la reazione avviene grazie alla conversione di parte dell'energia interna da cinetica in potenziale o viceversa (trasformazione adiabatica).
In altre parole una reazione in un sistema isolato  trasforma sempre parte dell'energia cinetica delle molecole (energia termica) in energia potenziale (energia chimica di legame) ed il sistema si raffredda, o, viceversa,  trasforma parte dell'energia di legame in energia termica ed il sistema si riscalda.

Tale affermazione è una conseguenza del primo principio della termodinamica che afferma che l'energia non si può né distruggere né creare, ma può solo essere convertita da una forma in un'altra.

Se invece il sistema può scambiare energia con l'intorno, il primo principio della termodinamica ci informa che la quantità di energia che il sistema scambia con l'ambiente esterno è esattamente pari alla sua variazione di energia interna.
In altre parole l'energia totale dell'universo (sistema + ambiente esterno) rimane sempre costante.
In realtà non è possibile calcolare l'energia interna di un sistema, ma solo le variazioni di energia che caratterizzano due stati diversi di un sistema (ciò è dovuto al fatto che parte dell'energia interna di un sistema è costituita da energia potenziale di cui, come sappiamo, non è possibile determinare un valore assoluto).

Se ad esempio un sistema chimico reagisce trasformando dei reagenti in prodotti di reazione, noi siamo in grado di misurare solo la variazione di energia interna E che si verifica durante la reazione, espressa come differenza tra l'energia interna dei prodotti di reazione (energia interna dello stato finale, Ef) e l'energia interna dei reagenti (energia interna dello stato iniziale, Ei)

E  =   Ef   −  Ei

Non ci è invece possibile misurare i valori assoluti di  Ef  ed Ei.

In un sistema isolato E  = 0 e la reazione avviene per conversione interna di una forma di energia in un'altra (cinetica in potenziale, o viceversa).

Nella maggior parte delle reazioni chimiche il sistema è in grado di scambiare energia con l'ambiente, per cui E  0.

 

Variazioni dell'energia interna E di un sistema chimico

Durante una reazione chimica l'energia interna di un sistema può variare essenzialmente poiché avvengono scambi di calore q e/o di lavoro w con l'ambiente esterno.
Determinare la variazione . E  di energia interna associata ad una reazione chimica significa misurare l’entità del calore e del lavoro scambiati dal sistema con l’ambiente.

Si tenga presente che i flussi di energia in uscita dal sistema, diminuendone l’energia interna, assumono valore negativo, mentre i flussi di energia in entrata nel sistema, aumentandone l’energia interna, assumono valore positivo.

Scambi di calore
Quando un sistema assorbe calore la sua energia interna aumenta, mentre quando un sistema cede calore la sua energia interna diminuisce. Per questo motivo al calore assorbito dal sistema viene assegnato valore positivo, mentre al calore ceduto viene assegnato valore negativo.

                                      A  +  B  +  q (calore) →  C  +  D                reazione endotermica

                                      A  +  B  −  q (calore)   →  C  +  D               reazione esotermica

La reazione esotermica può ovviamente essere scritta anche riportando il calore di reazione con il segno positivo tra i prodotti di reazione

  A  +  B   →  C  +  D  + q (calore)               reazione esotermica

Supponiamo ora per semplicità che una reazione avvenga solo con scambio di calore tra il sistema e l'ambiente. Potremo allora scrivere

E  =  q

In assenza di lavoro, lo scambio di calore è uguale alla variazione dell'energia interna del sistema
In pratica il calore scambiato in una reazione isocora (e in assenza di qualsiasi altro lavoro oltre a quello di espansione) può essere utilizzato come misura della variazione di energia interna di un sistema.

Prendiamo ad esempio la reazione di combustione del glucosio a 25°C ed 1 atm

                                   C6H12O6(s)  +  6O2(g)  →  6CO2(g)  + 6H2O(l) + 2808 kJ/mol

che possiamo anche scrivere

                                   C6H12O6(g)  +  6O2(g) - 2808 kJ/mol  →  6CO2(g)  + 6H2O(l)

a testimonianza del fatto che l'energia interna del sistema è diminuita di 2808 kJ per ogni mole di glucosio bruciato. Tale energia è stata completamente ceduta all'ambiente sotto forma di calore.
Per tale reazione possiamo scrivere

E  =  q  = − 2808 kJ/mol

In questo esempio il sistema ha scambiato solo calore con l'ambiente e per questo motivo la variazione di energia interna coincide con il calore scambiato, ma in generale durante le razioni chimiche un sistema può eseguire un lavoro sull'ambiente o, viceversa, l'ambiente può effettuare un lavoro sul sistema.

Scambi di lavoro
E' evidente che in questo caso l'energia interna del sistema varierà di conseguenza. Se il sistema esegue un lavoro sull'ambiente lo fa a spese della sua energia interna che diminuisce, mentre se l'ambiente effettua un lavoro sul sistema l'energia interna di quest'ultimo deve aumentare.
Per questo motivo al lavoro eseguito dal sistema viene assegnato valore negativo, mentre al lavoro subito dal sistema viene assegnato valore positivo.

Se teniamo quindi conto sia degli scambi di calore che del lavoro compiuto, la variazione di energia interna assume la forma

E  =  q + w

Tale relazione esprime in modo completo il primo principio della termodinamica, affermando che la variazione di energia interna di un sistema dipende dal calore scambiato con l'ambiente e dal lavoro eseguito durante la trasformazione.

Nella maggior parte delle reazioni chimiche il lavoro prodotto durante le trasformazioni è legato alle variazioni di volume del sistema in seguito ad un cambiamento nel numero totale delle moli delle specie chimiche gassose. In questo caso il sistema è libero di espandersi (se il numero di moli aumenta) eseguendo un lavoro sull’ambiente contro la pressione esterna (in genere la pressione atmosferica) o di contrarsi (se il numero di moli diminuisce) subendo un lavoro da parte dell’ambiente.

Ora è semplice dimostrare che il lavoro di espansione eseguito da un gas contro una pressione esterna costante P è pari a
wesp = − P . V

mentre il lavoro di contrazione subito da un gas sottoposto alla pressione esterna costante  P è pari a

wcont = + P . V
dove V è la variazione di volume
Infatti il  lavoro è dato dal prodotto di una forza F per lo spostamento x generato dalla medesima

w = F . x
ricordando tuttavia che la Pressione è il rapporto tra una forza F e la superficie di area A sulla quale essa agisce P = F/A e quindi F = P.A, potremo scrivere   w = P . A . x = P . V

 

Ricordando infine che la  variazione di volume V è pari a

il lavoro compiuto sarà allora pari a

Usando per la costante dei gas il valore R = 8,314 , si ottiene direttamente il lavoro espresso in joule.

 

Il sistema compie lavoro ( w negativo, l'energia interna diminuisce)
Se durante la reazione il numero complessivo delle moli gassose aumenta il sistema si espande utilizzando parte della sua energia interna per eseguire un lavoro, in genere contro l'atmosfera sovrastante. Il lavoro eseguito va a diminuire l'energia interna del sistema.

Prendiamo ad esempio in considerazione la reazione a 25°C e 1 atm

Zn(s) + 2HCl(aq) → ZnCl2(aq) + H2(g) + 153,89 kJ

La reazione libera 153,89 kJ sotto forma di calore ceduto all'ambiente, per cui l'energia interna del sistema diminuirà di conseguenza e potremo scrivere

                                                                       q = − 153,89 kJ

Durante la reazione si forma però una mole di idrogeno gassoso. Il sistema si espande compiendo un lavoro contro il peso dell'atmosfera sovrastante.

 

Calcoliamo allora il lavoro eseguito dal sistema durante l'espansione di 1 mole di idrogeno a 25°C e 1 atm

Possiamo allora affermare che non tutta l'energia ceduta dal sistema è stata dissipata come calore. Parte di essa è stata utilizzata dal sistema per eseguire un lavoro sull'ambiente pari a 2,48 kJ. Per questo motivo l'energia interna del sistema dovrà diminuirà dello stesso valore e di conseguenza potremo scrivere
w = − 2,48 kJ
La variazione complessiva dell'energia interna, tenendo conto sia del calore ceduto che del lavoro eseguito sarà allora pari a

E = q + w = ( − 153,89 kJ ) + ( − 2,48 kJ ) =  − 156,37 kJ

La diminuzione di energia interna risulta quindi in tal caso leggermente superiore alla cessione di calore, a causa del lavoro di espansione del sistema.

L'ambiente compie lavoro sul sistema  ( w positivo, l'energia interna aumenta)
Se durante la reazione il numero complessivo delle moli gassose diminuisce il sistema si contrae, subendo un lavoro di compressione, in genere da parte dell'atmosfera sovrastante. Il lavoro eseguito dall'ambiente va ad aumentare l'energia interna del sistema.

Prendiamo ad esempio in considerazione la reazione a 25°C e 1 atm

3H2(g) + N2(g)  → 2NH3(g)  + 92,22 kJ

La reazione avviene dunque con cessione all'ambiente di 92,22 kJ. Scriveremo

q = − 92,22 kJ

Durante la reazione il volume del sistema si è ridotto da quello occupato dalle 4 moli dei reagenti gassosi, alle  2 moli del prodotto di reazione.

Calcoliamo allora il lavoro subito dal sistema durante la contrazione alla pressione di 1 atmosfera

Possiamo allora affermare che l'energia interna del sistema diminuisce in misura minore rispetto al calore  ceduto, in quanto sul sistema viene compiuto del lavoro da parte dell'ambiente esterno pari a 4,95 kJ. Per questo motivo l'energia interna del sistema aumenterà di conseguenza e potremo scrivere
w = + 4,95 kJ

La variazione complessiva dell'energia interna, tenendo conto sia del calore ceduto che del lavoro eseguito sarà allora pari a

E = q + w = ( − 92,22 kJ ) + ( + 4,95 kJ ) =  − 87,37 kJ

La diminuzione di energia interna è quindi inferiore alla cessione di calore, in quanto la contrazione del sistema ha prodotto un leggero aumento di energia nel sistema.

Le reazioni che avvengono con diminuzione dell'energia interna di un sistema sono  dette  esoergoniche (E < 0).
Le reazioni che avvengono con aumento dell'energia interna di un sistema sono  dette   endoergoniche  (E > 0).

 

Entalpia (H)  e termochimica

Dagli esempi visti finora sulle interazioni che avvengono tra i sistemi chimici ed il loro intorno si è potuto osservare come gli scambi energetici più consistenti (quelli che incidono in misura maggiore sulla variazione dell'energia interna del sistema) sono quelli legati allo scambio di calore q tra il sistema ed il suo intorno.
Gli scambi di energia legati al lavoro compiuto sono in genere di minor entità e sono prevalentemente legati al lavoro di espansione o di contrazione del sistema (variazioni del volume V). Ciò è dovuto al fatto che la maggior parte delle reazioni chimiche viene condotta a pressione atmosferica, lasciando che il sistema vari liberamente il proprio volume alla pressione costante di 1 atm (pressione atmosferica) in relazione al numero di moli gassose presenti all'equilibrio.

Se ad esempio facciamo avvenire la reazione precedente di sintesi dell'ammoniaca in un contenitore chiuso, in cui il volume sia costante, il sistema non subisce lavoro da parte dell'ambiente.
La variazione di energia interna è la stessa (l’energia interna è infatti una funzione di stato), ma mentre in precedenza il sistema dissipava sotto forma di calore anche il lavoro di contrazione subito dall'ambiente, ora dissipa solo l'energia proveniente dalla riorganizzazione dei legami chimici.

E = q + w = ( − 87,37 kJ ) + ( 0 ) =  − 87,37 kJ

E' dunque fondamentale specificare se il calore di reazione (calore assorbito o ceduto durante la reazione) viene misurato a pressione costante qp o a volume costante qv.

In altre parole il calore di reazione a volume costante qv è una misura della variazione dell’energia interna del sistema (essendo w = 0)
E = qv

Tuttavia, come si è già detto, la maggior parte delle reazioni chimiche avviene a pressione costante, con il sistema, sottoposto alla pressione atmosferica, che risulta libero di variare il suo volume in funzione dell’eventuale variazione del numero di moli gassose che avviene durante la reazione

A questo proposito è di particolare interesse pratico l'entalpia (H), una funzione di stato il cui utilizzo risulta conveniente nel caso di reazioni isobare (a pressione costante) e poiché i processi isobari sono estremamente frequenti, il concetto di entalpia è di comune utilizzo.

L'entalpia non è una funzione di stato che discende, come l'energia interna, da considerazioni di tipo logico relativamente agli scambi energetici di un sistema, ma è una funzione di stato definita arbitrariamente e costruita secondo la seguente relazione

H  =  E  +  P.V

Consideriamo un sistema costituito da un liquido in presenza del suo vapore, contenuto in un cilindro chiuso da un pistone mobile a contatto con l’atmosfera. Se forniamo al sistema una quantità di calore qp evapora liquido, aumenta il volume e il sistema compie il lavoro w = − P (V2 –V1) sull’esterno. Quindi il primo principio può essere scritto nel modo seguente

E  = E2 – E1 =  qp + w = qp – P(V2 – V1)

quindi, riordinando
 (E2 + PV2) – (E1 + PV1 ) =  qp

e dunque
H2 – H1 = H = qp

Si introduce pertanto la nuova funzione di stato Entalpia H, la cui variazione H è pari al calore di reazione qp  misurato a pressione costante. Ciò significa che la misura del calore di reazione effettuata a pressione costante permette di ottenere direttamente le variazioni di entalpia.

In pratica si usa misurare il calore di reazione a pressione costante e a volume costante per ottenere rispettivamente una misura di H e E. In definitiva

per reazioni a pressione costante       H = qp  

per reazioni a volume costante        E= qv

 

Anche per l'entalpia non è possibile calcolare un valore assoluto, ma solo le sue variazioni (H)
Essendo una funzione di stato la variazione di entalpia non dipende dal percorso seguito durante la trasformazione, ma solo dagli stati estremi. Così potremo scrivere

H  =  Hfinale  –  Hiniziale

Ciò significa che la misura del calore di reazione effettuata a pressione costante permette di ottenere direttamente le variazioni di entalpia.

Naturalmente le reazioni che cedono calore all'ambiente presentano un H negativo e sono dette esotermiche, mentre le reazioni che assorbono calore presentano un H positivo e sono dette endotermiche

                                               reazioni esotermiche         H < 0

                                               reazioni endotermiche      H  > 0

Per questo motivo spesso si sente affermare che l'entalpia è il contenuto termico o calorico di un sistema (il termine stesso deriva dal greco 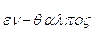 = calore interno). Tale affermazione non è tuttavia corretta. Il calore non può infatti essere inteso come un'entità posseduta da un corpo (come avviene per l'energia interna o l'energia cinetica), in quanto esso è misurabile solo all'atto dello scambio tra due corpi a diversa temperatura.

L'entalpia a pressione costante è una funzione di stato molto utilizzata in chimica, poiché permette di tener conto degli scambi termici che avvengono durante le reazioni (calori di reazione).
Naturalmente la variazione di entalpia associata ad una reazione (calore scambiato a pressione costante), essendo l'entalpia una funzione di stato, dipende dai valori assunti dalle variabili di stato (P, V, T).
Allo scopo di standardizzare i dati si è perciò convenuto di misurare il calore scambiato alla pressione costante di 1 atmosfera e alla temperatura di 25°C.

Le variazioni di entalpia misurate in tali condizioni sono dette standard ed indicate come H°.
Inoltre, poiché non è possibile assegnare un valore assoluto all'entalpia dei diversi composti chimici in condizioni standard ( 1 atm e 25°C), si è convenuto di prendere come stato entalpico di riferimento, assegnando loro H° = 0, gli elementi chimici nel loro stato standard.

In tal modo la variazione di entalpia che intercorre nella reazione di sintesi di un composto a partire dai suoi elementi costituenti può essere convenzionalmente assunta come entalpia di formazione del composto stesso.

Sia ad esempio la reazione di sintesi dell'acqua (a pressione atmosferica) a partire dagli elementi costituenti nel loro stato standard

2H2(g)  +  O2(g)  →  2H2O(l) + 571,66 kJ

La reazione è esotermica 
qp  =  – 571,66 kJ
ed avvenendo a pressione costante
H° = qp =  – 571,66 kJ
Ma la variazione di entalpia è pari a

H° = H°finale - H°iniziale  = H°acqua - (H°idrogeno + H°ossigeno)

essendo convenzionalmente l'entalpia standard degli elementi pari a zero, avremo

(H° idrogeno + H° ossigeno) = 0

e quindi, l'entalpia di formazione di 2 moli di acqua sarà pari a

H° = H°acqua - (H° idrogeno + H° ossigeno) = H°acqua - 0 = H°acqua =  – 571,66 kJ

Naturalmente il valore per mole sarà pari a

Le entalpie di formazione standard di molti composti si trovano tabulate assieme ai H° di combustione, ai H° di fusione, ai H° di evaporazione etc.
I valori di entalpia tabulati per i diversi composti possono essere utilizzati per calcolare i calori di reazione di trasformazioni chimiche anche molto complesse.
Le regole di combinazione delle entalpie dei vari composti nelle trasformazioni chimiche sono dettate dalle due leggi della termochimica: la legge di Lavoisier-Laplace e la legge di Hess
.

Legge di Lavoisier-Laplace (1780)

Il calore richiesto per decomporre una sostanza è uguale al calore sviluppato durante il processo di formazione.
Possiamo riformulare in termini moderni l'enunciato di tale legge, affermando che se si inverte il verso di una reazione chimica è sufficiente invertire il segno del H, mantenendone inalterato il valore assoluto.
Prendiamo ad esempio la reazione di decomposizione dell'ammoniaca a 25°C

                        2NH3(g) → N2(g) + 3H2(g)                               H°  = + 92,22 kJ

Per la legge di Lavoisier-Laplace possiamo prevedere che la reazione opposta, di sintesi, presenti una variazione di entalpia uguale e contraria

                        N2(g) + 3H2(g)  → 2NH3(g)                              H°  =  – 92,22 kJ

 

Legge di Hess (1840)

La somma algebrica dei calori prodotti o assorbiti durante un processo chimico a più stadi è uguale al calore prodotto o assorbito nel caso la stessa reazione avvenga attraverso uno stadio unico.

In termini moderni la legge di Hess afferma che il H di una reazione può essere ottenuto mediante somma algebrica dei H dei singoli stadi in cui si può eventualmente suddividere la reazione stessa.

Supponiamo ad esempio che la reazione
A   →   B
possa essere suddivisa nei seguenti stadi

                                                           A  →  X  →  Y  →  Z →  B

possiamo allora rappresentare le relative variazioni di entalpia attraverso il seguente grafico

                                         

e la legge di Hess attraverso la seguente relazione

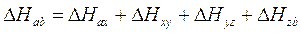
Naturalmente entrambe le leggi della termochimica sono una diretta conseguenza del fatto che l'entalpia è una funzione di stato e i valori che essa assume negli stati iniziale e finale sono indipendenti dal percorso effettuato.

Applicando le leggi della termochimica è possibile calcolare valori di H° non tabulati e calori di reazione che non possono essere misurati sperimentalmente.

Vediamo alcuni esempi

1) Vogliamo calcolare il H° di formazione del glucosio, sapendo che il suo H° di combustione è pari a - 2808 kJ/mol e che il H° di formazione dell'anidride carbonica gassosa e dell'acqua liquida sono rispettivamente -393,51 kJ/mol e -285,83 kJ/mol.

Il problema chiede di calcolare la variazione di entalpia della  reazione di sintesi del glucosio a partire dagli elementi che lo costituiscono

6C + 6H2 + 3O2  → C6H12O6

Conosciamo il H° di combustione del glucosio

C6H1206  +  6O2    → 6H2O + 6CO2        H° =  – 2808 kJ/mol

Per la legge di Lavoisier-Laplace il  H° della reazione inversa vale

                1)           6H2O + 6CO2   →   C6H1206  +  6O2        H°1 = + 2808 kJ/mol 

Conosciamo inoltre i H° di formazione dell'anidride carbonica e dell'acqua. Per 6 molecole possiamo scrivere

                 2)          6C + 6O2 →  6CO2              H°2 =   – 393,51 kJ/mol . 6moli =  – 2361,06 kJ

               3)          6H2 + 3O2 →  6H2O            H°3 =   – 285,83 kJ/mol . 6moli =  – 1714,98 kJ

Osserviamo ora come sommando, membro a membro, le reazioni 1), 2) e 3) si possa ottenere la reazione di formazione del glucosio dai suoi elementi, di cui vogliamo calcolare l'entalpia

                                               6H2O + 6CO2            →        C6H12O6  +  6O2         +
6C + 6O2                    →        6CO2                                  +
6H2 + 3O2                  →        6H2O                          =
                                      

Semplificando le specie chimiche che compaiono in entrambi i membri si ottiene

                4)                                

Poiché dunque la reazione 4) si può ottenere come somma delle tre reazioni parziali precedenti, applicando la legge di Hess, possiamo calcolare il suo H° come somma dei tre  H° parziali.

H°4   =  H°1  + H°2 + H°3

H°4   =    (+ 2808) + ( – 2361,06) + ( – 1714,98) =  – 1268,04 kJ

2) La determinazione sperimentale del H° di formazione dell'ossido di carbonio dagli elementi è estremamente difficoltosa, in quanto, oltre all'ossido di carbonio si forma sempre una certa quantità di anidride carbonica. Il H° può essere comunque calcolato per via teorica, applicando le leggi della termochimica.

La reazione di cui si vuole calcolare il H° è la seguente

                                   1)                    2C  +  O2  → 2CO                            H°1 = ?

Tale reazione  non si produce però mai da sola, poiché parte dell'ossido di carbonio reagisce con l'ossigeno per dare anidride carbonica, secondo la reazione

                                   2)                    2CO   +  O2  →  2CO2                         H°2 =  – 566,0 kJ         

della quale possiamo misurare sperimentalmente il H°

3)                    C   +   O2 → CO2                              H°3 =  – 393,5 kJ

della quale possiamo misurare sperimentalmente il H°, ottenendo la completa ossidazione, mediante combustione del carbonio con un eccesso di ossigeno.

Osserviamo ora che la reazione 3) può essere ottenuta come somma delle prime due

                                                           2C  +  O2        →        2CO    +
2CO   +  O2    →        2CO2   =
                                                  
2C  +  2O2      →        2CO2

Naturalmente bisognerà tener conto che il della reazione 3) dovrà essere moltiplicato per 2 per rendere omogeneo il numero di moli con le reazioni 1) e 2).
Potremo allora scrivere
H°1 + H°2 = H°3
e quindi
H°1  = H°3 - H°2

H°1  = ( – 787,0 kJ) – ( – 566,0 kJ) =  – 221,0 kJ

Il H° di formazione dell'ossido di carbonio (per mole di CO) a partire dagli elementi costitutivi sarà allora pari a

H° =  – 110,5 kJ/mol

3) In generale per calcolare il H° di una reazione chimica è sufficiente sottrarre alla somma delle entalpie dei prodotti, la somma delle entalpie dei reagenti.
Si voglia ad esempio calcolare il H° della seguente reazione

CaCO3(s)  +  2HCl(aq)   →   CaCl2(s) +H2O(l) + CO2(g)

sapendo che le entalpie di formazione (valori tabulati) delle diverse specie chimiche sono

 

CaCO3(s)           H° =   – 1206,9  kJ/mol
HCl(aq)               H° =   – 167,2    kJ/mol
CaCl2(s)              H° =   – 795,8    kJ/mol
H2O(l)                 H° =   – 285,8    kJ/mol
CO2(g)                 H° =   – 393,5    kJ/mol

il H° della reazione sarà allora pari a

            H°  =   [(– 795,8)  +  (– 285,8)  + (– 393,5)]  –  [(–1206,9) + 2.( – 167,2)] =   – 66,2 kJ

 

Entropia (S), Energia libera (G) e criteri di spontaneità

 

Le variazioni energetiche (E o H) che accompagnano una reazione chimica completano la descrizione che noi possiamo dare di una trasformazione e, nella maggior parte dei casi, forniscono delle indicazioni di massima sul verso naturale della reazione, in quanto la maggior parte delle reazioni esotermiche (ed esoergoniche) risulta spontanea.
D'altra parte esistono numerose eccezioni a questo assunto  e  non tutte le reazioni  che  presentano un H (o un E) negativo risultano poi spontanee.
Diventa perciò necessario individuare un criterio di spontaneità che ci permetta di prevedere il verso delle reazioni in modo esauriente e generale.

Inoltre la maggior parte delle reazioni non avviene in modo completo, ma si assesta in uno stato di equilibrio in cui vi è la presenza di una miscela di reagenti e prodotti di reazione in rapporti determinati e calcolabili sulla base dei valori delle costanti di equilibrio.
Dovremo pertanto stabilire un criterio di spontaneità in grado di descrivere non solo il verso naturale di una trasformazione, ma anche di giustificare perché un sistema tende in certe condizioni a raggiungere spontaneamente un punto di equilibrio piuttosto che un altro.

Il criterio generale che permette di prevedere il verso spontaneo di qualsiasi trasformazione, fisica o chimica che sia, e di descrivere la tendenza dei sistemi verso particolari condizioni di equilibrio discende dal secondo principio della termodinamica.

Vi sono diversi modi equivalenti con cui è possibile definire il secondo principio. Uno di questi ci permette di individuare contemporaneamente anche un criterio generale di spontaneità delle trasformazioni: il grado di disordine dell'universo può solo aumentare ed una trasformazione spontanea è sempre accompagnata da un aumento del disordine complessivo dell'universo.

Possiamo dunque prevedere che un sistema non si trovi in equilibrio fino a quando possa modificare il suo stato verso condizioni di maggior disordine complessivo. Esso evolverà spontaneamente verso stati maggiormente disordinati e le condizioni di equilibrio saranno invece caratterizzate da condizioni di massimo disordine.
E' a questo punto evidente che per effettuare delle previsioni relativamente al verso spontaneo delle trasformazioni e al raggiungimento di condizioni di equilibrio, dobbiamo essere in grado di quantificare e misurare il disordine di un sistema.

La funzione di stato in grado di misurare il disordine di un sistema è l'entropia.

Per l'entropia (S) di un sistema, a differenza di quanto avviene per le altre funzioni di stato, è possibile calcolare dei valori assoluti.

Il terzo principio della termodinamica afferma infatti che l'entropia è nulla per gli elementi chimici nella loro forma cristallina allo zero assoluto (0 K).

Il calcolo dell'entropia può essere effettuato utilizzando la relazione di Clausius

dove
Q = calore scambiato dal sistema
T = temperatura assoluta

 

oppure utilizzando la relazione di Boltzmann

dove
k = costante di Boltzmann (R/N) = 1,38.10-23 J/ K
n = numero di diverse combinazioni di microstati in grado di dare lo stesso macrostato

 

Nella pratica le misure sperimentali di entropia si eseguono misurando le capacità termiche delle sostanze chimiche a temperature vicine allo zero assoluto (si misura cioè la quantità di calore assorbito per aumentare di 1 grado la temperatura per T 0).
L'entropia si misura in J/ K (Joule su Kelvin).

Le misure sperimentali di entropia per gli elementi allo stato puro a temperature vicine allo zero assoluto forniscono buone conferme del terzo principio della termodinamica (principio di Nernst), confermando che l'entropia di tali solidi cristallini in queste condizioni tende a zero.

I solidi elementari sono infatti formati da atomi tutti identici ed allo zero assoluto essi occupano in modo rigido delle posizioni perfettamente definite all'interno del reticolo cristallino. In queste condizioni il sistema è perfettamente ordinato e vi è un'unica configurazione possibile delle particelle che lo costituiscono. Applicando la relazione di Boltzmann, poiché n = 1,         S = k . ln 1 = 0

 

Le misure sperimentali di entropia per i composti a temperature vicine allo zero assoluto forniscono invece valori di entropia superiori allo zero. Ad esempio l'entropia di 1 mole di ossido di carbonio CO a temperature tendenti a 0 K è pari a 4,6 J/K.
Nel caso di composti chimici infatti le molecole sono composti da atomi differenti. Nel caso dell'ossido di carbonio possiamo ad esempio supporre che le molecole di CO possano disporsi nel reticolo secondo due orientazioni distinte (CO e OC). Se il solido fosse composto da due sole molecole  esse potrebbero dar luogo a 22 = 4 combinazioni diverse. In tal caso   n = 4

CO CO             CO OC           OC CO           OC OC

Se il solido fosse composto da tre molecole  esse potrebbero dar luogo a 23 = 8 combinazioni diverse.
Nel caso in questione, prendendo in considerazione una mole di CO e quindi 6,022.1023 molecole,  il numero di possibili combinazioni è

L'entropia teorica, calcolabile attraverso la relazione di Boltzmann è quindi     

valore in buon accordo con i dati sperimentali.

Man mano che una sostanza viene riscaldata aumenta il suo disordine interno e quindi anche la sua entropia.

Anche per l'entropia è stato fissato uno stato standard che, in analogia a quanto convenuto per l'energia interna e per l'entalpia, è definito come l'entropia di una  mole di sostanza a 25°C e 1 atm (S°). In pratica  l'entropia molare standard di ogni sostanza viene calcolata misurando il calore assorbito da una mole di sostanza alle varie temperature fino ad arrivare a 298 K e sommando poi i diversi apporti calorici da 0 K a 298 K.
Una volta note le entropie standard delle diverse sostanze chimiche è possibile calcolare la variazione di entropia associata ad una reazione chimica come

S° = S°prodotti  -  S°reagenti

Ad esempio nella reazione

N2  +   3H2      2NH3             H° =  - 92,22 kJ

la variazione di entropia della trasformazione è pari a   

L'entropia del sistema è diminuita. Ciò è dovuto al fatto che i prodotti di reazione sono costituiti da un numero minore di particelle tutte dello stesso tipo, mentre i reagenti sono costituiti da un numero maggiore di particelle e per di più di tipo diverso (azoto e idrogeno). I reagenti possono quindi configurarsi in un numero di modi diversi molto maggiore di quanto non riescano a fare i prodotti di reazione.
In generale possiamo prevedere che l'entropia (e quindi il disordine) di un sistema aumenti durante una reazione chimica quando aumenta il numero delle specie chimiche diverse ed il numero totale delle particelle (o moli) presenti.

Nonostante la reazione di sintesi dell'ammoniaca decorra con una diminuzione dell'entropia del sistema, essa risulta egualmente spontanea a 25°C.
Infatti per poter decidere sulla spontaneità o meno di una reazione non è sufficiente analizzare solo le variazioni di entropia del sistema, ma anche le variazioni di entropia che la trasformazione del sistema genera sull'ambiente.
In altre parole se la variazione di entropia del sistema, sommata alla variazione di entropia dell'ambiente (variazione di entropia dell'universo) indotta da una trasformazione risulta complessivamente positiva, allora la trasformazione risulta spontanea.

Stotale = Ssistema + Sambiente > 0

Nelle reazioni chimiche a pressione costante (la maggior parte) la variazione di entropia dell'ambiente è direttamente collegabile al calore che il sistema scambia con il suo intorno. Così se il sistema subisce una trasformazione esotermica isobara cedendo all'ambiente una quantità di calore Q = H, è possibile dimostrare che la variazione di entropia dell'ambiente (a pressione e temperatura costanti) è pari a

In altre parole è possibile calcolare la variazione di entropia dell'ambiente sulla base delle variazioni di entalpia del sistema.

Il criterio generale di spontaneità di una trasformazione potrà allora essere espresso come

Stotale = Ssistema  > 0

Comunemente tale relazione viene riscritta nella forma

< 0

Il prodotto -T.Stotale viene definito come variazione di una nuova funzione di stato, chiamata Energia libera G (da Gibbs, lo scienziato americano che per primo ne propose l'introduzione)

< 0
Risulta pertanto spontanea una reazione per la quale la variazione totale di entropia è positiva o, utilizzando la funzione di stato G, per la quale risulti negativa la variazione di energia libera.

Applicando tale definizione alla reazione di sintesi dell'ammoniaca possiamo calcolare le variazioni di entropia totale e di energia libera e verificare che la reazione risulta spontanea.

Stotale =

Come si può osservare, nonostante la trasformazione produca una diminuzione dell'entropia del sistema (-198,75 J/K) lasciandolo più ordinato, il calore ceduto all'ambiente durante la reazione aumenta l'entropia dell'ambiente stesso (+ 309,46 J/K) in misura talmente sensibile che l'entropia totale dell'universo (sistema + ambiente) è destinata ad aumentare ( + 110,71 J/K) durante la reazione.

Il calcolo della variazione dell'energia libera ci fornisce naturalmente un valore negativo, confermandoci che la reazione è spontanea

Naturalmente anche per l'energia libera è stato definito uno stato standard.
Si definisce Energia libera molare standard (G°) di formazione di un composto la variazione di energia libera a 25°C ed 1 atm associata alla formazione di una mole del composto a partire dagli elementi semplici.
Convenzionalmente si pone (in analogia con quanto visto per l'Entalpia) pari a zero l'Energia libera degli elementi nel loro stato standard.
I valori dei G° sono tabulati ed è naturalmente possibile utilizzarli per calcolare la variazione di energia libera associata a qualsiasi reazione, attraverso la seguente relazione

G° =   (G°prodotti) - (G°reagenti)

Si voglia ad esempio calcolare la variazione di Energia libera standard della seguente reazione

CaCO3(s)  → CaO(s) + CO2(g)

sapendo che i G° di formazione dei diversi composti sono

                                               G°     CaCO3(s)           = -1128,8 kJ/mol
G°     CaO(s)                 = - 604,03 kJ/mol
G°     CO2(g)                  = - 394,36 kJ/mol

G° =   (G°prodotti) - (G°reagenti) = [(- 604,03) + (- 394,36)] - (- 1128,8) = + 130,41 kJ

Essendo il G° > 0 la reazione non è spontanea. E' naturalmente spontanea la reazione opposta.

Si può dimostrare che l’energia libera è una misura della massima quantità di lavoro non legato all’espansione che può eseguire un sistema, detto anche lavoro utile. Questo è il motivo per il quale l’energia di Gibbs è detta energia libera (anche se oggi si preferisce chiamarla energia di Gibbs).

 

Previsioni sulla spontaneità di una reazione

L'equazione di Gibbs per il calcolo dell'Energia libera è formata da un termine energetico (H) e da un termine entropico (TS) che possono influire in modo diverso sulle variazioni di Energia libera del sistema.

Possiamo prendere in considerazioni 4 casi

1) Reazioni esotermiche (H < 0) con S > 0 (aumento Entropia)
Si tratta di reazioni sicuramente spontanee. E' infatti facile verificare che in tal caso  la  variazione del G non può essere che negativa.

2) Reazioni endotermiche  (H > 0) con S < 0 (diminuzione Entropia)
Si tratta di reazioni sicuramente non spontanee. E' infatti facile verificare che in tal caso la variazione del G non può essere che positiva.

3) Reazioni esotermiche (H < 0) con S < 0 (diminuzione Entropia)
In tal caso il termine energetico e quello entropico si muovono in direzioni opposte. Il termine energetico (H) tende a rendere spontanea la reazione, quello entropico (S) tende a contrastarla. E' evidente che in questo caso è necessario verificare quale dei due termini prevale sull'altro. In generale il termine energetico risulta maggiore, a 25°C, rispetto al termine entropico, per cui la maggior parte di queste reazioni risulta spontanea a temperatura ambiente.
La spontaneità di tali reazioni tende invece ad annullarsi ad elevate temperature, in quanto il termine entropico diventa più importante, dovendo essere moltiplicato per T.
La sintesi dell'ammoniaca è un esempio di questo tipo di reazioni.

4) Reazioni endotermiche  (H > 0) con S > 0 (aumento Entropia)
Anche in tal caso il termine energetico e quello entropico si muovono in direzioni opposte. Il termine entropico (S) tende a rendere spontanea la reazione, quello energetico (H) tende a contrastarla. Anche in questo caso è necessario verificare quale dei due termini prevale sull'altro. In generale il termine energetico risulta maggiore, a 25°C, per cui la maggior parte di queste reazioni non risulta spontanea a temperatura ambiente.
Tali reazioni tendono invece a divenire spontanee ad elevate temperature, in quanto il termine entropico, che in questo caso presenta un effetto positivo sulla spontaneità, diventa più importante ad elevate temperature, dovendo essere moltiplicato per T.
Tipici esempi di tali reazioni sono i processi di solubilizzazione (endotermici) di molti soluti solidi.
Ad esempio la reazione di solubilizzazione del nitrato di ammonio (NH4NO3) è fortemente endotermica (H° = + 28,05 kJ) tanto che quando viene messo in acqua il recipiente si raffredda vistosamente. Ciononostante la reazione risulta spontanea a 25°C in quanto le soluzioni risultano molto più disordinate rispetto ai soluti solidi dai quali derivano. In questo caso particolare l'aumento di entropia è pari a S° = +108,72 J/K. La variazione di energia libera della reazione

NH4NO3  → NH4+   +   NO3-
è pertanto pari a

 

Energia libera e sistemi all'equilibrio

Abbiamo visto come un sistema tenda ad evolvere spontaneamente verso uno stato che presenta un DG < 0, mentre un DG > 0 implica una trasformazione non spontanea. È allora evidente come un  DG = 0 sia associabile ad una situazione di equilibrio in cui il sistema non manifesta alcuna tendenza a subire trasformazioni. In altre parole il sistema non può più compiere lavoro utile.

 

Transizioni di fase: Regola di Trouton

 

Calcoliamo la variazione di Energia libera per il processo di solidificazione dell'acqua a 0°C

H2O(l)  →  H2O(s)
sapendo che l'entropia dell'acqua e del ghiaccio a 0°C sono rispettivamente pari  a  65,2  (i liquidi sono più disordinati dei solidi) e che il processo è esotermico (H = - 6,00 kJ/mol), poiché durante la solidificazione  viene rilasciato il calore latente.

La variazione di Entropia durante il processo di solidificazione sarà pari a

S = 65,2 - 43,2 = 22,0 J/K

La variazione di Energia libera sarà

Ciò significa che l'aumento di disordine dell'ambiente che si produce durante il processo di congelamento (a causa della dissipazione di calore) viene esattamente controbilanciato dall'aumento di ordine del sistema. In altre parole a 0°C il sistema non presenta alcuna tendenza, né verso la fase solida, né verso la fase liquida. L'indifferenza del sistema si traduce in uno stato di equilibrio tra liquido e solido.

In effetti ciò è esattamente quello che accade. A 0°C l'acqua non ghiaccia, ma vi è equilibrio tra la fase liquida e la fase solida.
Possiamo dunque affermare che in generale un sistema raggiunge uno stato di equilibrio quando la variazione di Energia libera si annulla. In questo stato l'entropia dell'universo rimane costante ed il sistema non evolve spontaneamente in alcuna direzione.

 

Un’interessante applicazione si ha nel caso di un passaggio di stato liquido-aeriforme, in cui il liquido è in equilibrio con il proprio vapore. Si avrà allora

da cui si ricava la regola di Trouton, che permette di stimare in modo approssimato l’entalpia di evaporazione di un liquido, conoscendo la sua temperatura di ebollizione

 J K-1 mol-1

Il significato della regola di Trouton è che quando i liquidi evaporano si produce una quantità di disordine, ovvero entropia, che è pressappoco la stessa per le diverse sostanze. La relazione fornisce valori attendibili per liquidi non associati, di massa molecolare intorno a 100 e con temperatura di ebollizione non troppo alta. Tuttavia se le molecole del liquido sono ordinate in un modo particolare, come per esempio nel caso di acqua od etanolo in cui sono presenti nel liquido forti legami a idrogeno intermolecolari, allora l’entropia di evaporazione risulta superiore a quanto prevede la regola di Trouton, come risulta dalla seguente tabella di valori sperimentali.

Entropie di evaporazione

 

Transizioni di fase: Equazione di Clausius-Clapeyron

Per un generico passaggio di stato o di fase di un sistema costituito da una unica specie chimica, nel quale cioè le due fasi hanno uguale composizione e sono in reciproco equilibrio, vale l’equazione di Clapeyron (ottenuta eguagliando le energie libere di ciascuna fase).

dove
ΔHPdS = è l’entalpia associata al passaggio di stato A→B
VA = volume occupato dalla fase A
VB = volume occupato dalla fase B

a) Nel caso dell’equilibrio solido-liquido l’equazione di Clapeyron si scrive

Introducendo per semplicità l’approssimazione che DHfus e  DV siano,entro certi limiti, indipendenti dalla temperatura,  integrando si ottiene

Sottraendo membro a membro la relazione per due diverse temperature T1 e T2 si arriva all’equazione approssimata della curva di coesistenza solido-liquido:

La pendenza della curva solido-liquido dipende dal segno di ΔV. La maggior parte delle sostanze ha una pendenza positiva della curva di fusione (all’aumentare della pressione la temperatura di fusione aumenta) in quanto la fase liquida presenta un volume maggiore della fase solida (ΔV = Vliquido – Vsolido > 0).  L’acqua `e una nota eccezione, poiché ΔV < 0 (il ghiaccio è meno denso e quindi più voluminoso dell’acqua liquida)

Esempio Valutare la variazione di pressione necessaria per abbassare di 1 °C il punto di fusione del ghiaccio, sapendo che la densità dell’acqua è pari a 0.9998 g cm-3 e quella del ghiaccio è pari a 0.917 g cm-3, assumendo che il valore del ΔHfus sia indipendente dalla pressione e sia pari 6.0095 kJ mol-1. Calcoliamo il volume occupato da una mole di acqua (peso molare = 18,015 g mol-1) liquida e solida ed il relativo ΔV V (ghiaccio) =  = 19.6456 cm3 mol -1 =  19.6456 10-6 m3 mol -1, V(acqua) = = 18.0186 cm3 mol -1 =  18.0186 10-6 m3 mol -1 ΔV = Vacqua – Vghiaccio = -1.62710-6 m3 mol -1 Sostituiamo ora i valori nella equazione di Clapeyron e ricordando che 1 atm = 101325 Pa  = 1.36484 107 Pa = 134.7 atm Il movimento dei ghiacciai contro ostacoli rocciosi è attribuito in parte a questo abbassamento del punto di fusione indotto dalla forte pressione esercitata dalla massa di ghiaccio contro la roccia.

 

b) Se una delle due fasi è gassosa e quindi nel caso di equilibrio fase condensata-fase gassosa, si possono fare le seguenti approssimazioni:

• si ammette che il volume occupato da una mole della specie chimica allo stato liquido o solido sia trascurabile rispetto a quello occupato dalla stessa mole di vapore.
• si ammette che il vapore abbia comportamento ideale e si applica ad esso l’equazione di stato del gas ideale

In base a queste approssimazioni, essendo

e

l’equazione di Clapeyron per il passaggio di fase di 1 mole in cui una delle fasi è un gas si presenta nella forma seguente, nota come equazione di Clausius-Clapeyron

che, integrata, diventa

e trasformando il logaritmo neperiano in un logaritmo in base 10 (coefficiente di conversione 2,3), l'equazione di Clausius-Clapeyron diventa

ponendo poi la costante di integrazione pari a k = ln(A), l’equazione di Clausius-Clapeyron può essere scritta nella seguente forma esponenziale

 

con A che dipende dalla natura della specie chimica, in cui si osserva che la tensione di vapore di un liquido cresce esponenzialmente con la temperatura T

 

Nei diagrammi di fase le curve della tensione di vapore del liquido e del solido sono calcolabili attraverso l’equazione di Clausius-Clapeyron

Sottraendo membro a membro l’equazione di Clausius-Clapeyron per due diverse temperature T1 e T2 si ottiene l’equazione di Clausius-Clapeyron in una forma che lega le tensioni di vapor saturo di un liquido a due diverse temperature

Questa relazione si può usare per prevedere la pressione di vapore ad una data temperatura conoscendo DH  ed una pressione di riferimento.

Esempio Calcolare la pressione di vapore del toluene a 20°C sapendo che la temperatura di ebollizione è 110.6 °C e che l’entalpia di evaporazione è 35.2 kJ mol -1. Alla temperatura di ebollizione di 110.6 + 273.15 = 383.75K la pressione di vapore è per definizione 760 mmHg. Quindi  = 25 mm Hg

 

Inoltre l’equazione di Clapeyron serve per ricavare il DHevap da valori noti di pressione e temperatura.

Esempio Ricavare l’entalpia di evaporazione del benzene dai dati seguenti: P1 (a 70 °C) = 547.4 mm Hg;        P2 (a 80 °C) = 753.6 mm Hg  = 32.2 kJ mol -1.

Riportando in diagramma i valori del logaritmo naturale della pressione in funzione dell’inverso della temperatura si ottengono rette di pendenza -DHevap .

 

Energia libera e costante di equilibrio

Un’altra applicazione si ha nel calcolo delle costanti di equilibrio
Il valore di G° di una reazione chimica deve essere infatti in relazione allo stato di equilibrio che il sistema può raggiungere. In particolare in chimica le condizioni di equilibrio di un sistema vengono descritte tramite opportune costanti di equilibrio (kc, kp, ka, kb, kps, kw etc). Deve allora esistere una relazione che colleghi il G° di una reazione chimica alla relativa costante di equilibrio K.

Il G° di una sostanza è calcolato in condizioni standard (25°C, pressione parziale di 1 atm, concentrazione 1M). Si può dimostrare che il G in condizioni diverse da quelle standard varia con la concentrazione (o la pressione parziale per le sostanze gassose). Per una generica sostanza A la relazione è la seguente

Per una generica reazione del tipo

aA + bB      cC + dD

La variazione di Energia libera in condizioni non standard vale

E' facile verificare che, se la reazione era spontanea e quindi con un G° negativo, man mano che i reagenti si trasformano nei prodotti di reazione il rapporto delle loro concentrazioni aumenta fino al punto in cui il G della reazione non si azzera.

In queste condizioni ( G = 0) il sistema non presenta alcuna tendenza ad evolvere nè verso i reagenti, nè verso i prodotti di reazione. Il sistema ha raggiunto l'equilibrio ed il rapporto delle concentrazioni di equilibrio è proprio la costante di equilibrio K della reazione.
Potremo allora scrivere, per lo stato di equilibrio

che rappresenta la relazione cercata tra G° e K. Tale relazione può essere ottenuta per qualsiasi costante di equilibrio.

Calcoliamo ad esempio il prodotto di solubilità kps dello ioduro di argento AgI, sapendo che i G° di formazione delle specie chimiche interessate all'equilibrio sono

G°  AgI(s)      = - 66,19 kJ/mol
G° Ag+(aq)     = +77,11 kJ/mol
G° I-(aq)         = - 51,57 kJ/mol

AgI(s)         Ag+(aq)   +  I–(aq)

G° =   (G°prodotti) - (G°reagenti) = [(+ 77,11) + (- 51,57)] - (- 66,19) = + 91,73 kJ

Calcoliamo ora la kps

Calcoli analoghi possono essere fatti per tutte le altre costanti di equilibrio. A titolo di esempio calcoliamo la tensione di vapore dell'acqua a 25°C e la kb dell'ammoniaca.

1) Calcolare la costante di equilibrio kp dell'equilibrio di evaporazione dell'acqua

H2O(l)       H2O(g)

sapendo che il G° dell'acqua liquida e del vapor d'acqua vale rispettivamente - 237,13 kJ/mol e -228,57 kJ/mol.

 G° =   (G°prodotti) - (G°reagenti) = (-228,57)  - (- 237,13) = + 8,56 kJ

Calcoliamo ora la kp

Poiché la concentrazione dell'acqua liquida viene considerata costante, la kp di tale trasformazione coincide con la pressione parziale della fase gassosa e quindi con la tensione di vapor d'acqua a 25°C.

2) Calcoliamo ora la kappa basica kb dell'ammoniaca NH3, sapendo che i G° di formazione delle specie chimiche interessate all'equilibrio sono

 

G°  NH3(aq)    = - 26,5 kJ/mol
G° H2O (l)     = - 237,13 kJ/mol
G° NH4+(aq)   = - 79,31 kJ/mol
G° OH- (aq)     = - 157,24 kJ/mol

NH3(aq)  + H2O(l)      NH4+(aq)  +  OH-(aq)

 G° =  (G°prodotti) - (G°reagenti) = [(- 79,31) + (- 157,24)] -  [(- 26,5) + (- 237,13)] = +27,08 kJ

Calcoliamo ora la kb

Relazione tra  ΔG° e E°

La relazione esistente tra  G° e la costante di equilibrio è sostanzialmente analoga a quella esistente tra il potenziale standard E° e la costante di equilibrio per le reazioni redox

Riscrivendo la prima in funzione di K e sostituendo opportunamente nella seconda, otteniamo la seguente relazione tra G° e E°

analoga alla relazione che ci permetteva di calcolare il lavoro eseguibile da una pila.

Calcoliamo ad esempio il G° dello ione alluminio, sapendo che il potenziale standard di riduzione della coppia redox Al3+/Al  è E° = - 1,663 V

La reazione di cui vogliamo calcolare il G°  è la seguente

Al3+  + 3e-   →  Al
Calcoliamo il  G° della reazione

Calcoliamo ora il G° dello ione alluminio, ricordando che il G° degli elementi è convenzionalmente nullo

G° =  (G°prodotti) - (G°reagenti) =  0 -  X = + 481,3 kJ

e quindi

 

La costante di equilibrio K per temperature diverse da 25°C – Equazione di van’t Hoff

 

La relazione  
 

è valida a qualsiasi temperatura. I valori di H e di S variano in modo trascurabile al variare della temperatura, mentre G è fortemente dipendente dalla temperatura. E' allora  possibile stimare il valore di G alla generica temperatura T, utilizzando i valori tabulati (supposti costanti) di H° e di S° alla temperatura di 25°C.

In modo analogo si calcola la costante di equilibrio K(T) alla temperatura T diversa da 298,15 (T°). Dividendo ambo i membri della 2) per -RT si ottiene

 

Ricordando poi che

e

sostituendo opportunamente nella 4) si ottiene

da cui

e infine
   

La relazione (di van't Hoff) vale per due temperature qualsiasi, ma è particolarmente utile se T° = 298,15 K in quanto i valori delle grandezze termodinamiche sono tabulati per tale temperatura. In questo caso la  5) diventa      

 

(Il fattore 103 trasforma i kiloJoule in Joule)

 

ESEMPIO
Sapendo che la Kc a 25°C della reazione H2(g) + Cl2(g) « 2HCl(g) è pari a 4,0 1031, calcolarne il valore a 500 K.
Dai valori tabulati a 25°C delle funzioni termodinamiche ricaviamo i H° delle specie chimiche. Il H° della reazione sarà

Il valore della costante di equilibrio sarà allora pari a

 

 

 

fonte: http://www.pianetachimica.it/didattica/documenti/Chimica_Generale.doc

 

Termodinamica

 

 

Visita la nostra pagina principale

 

Termodinamica

 

Termini d' uso e privacy