La meccanica ondulatoria di Schroedinger

Questo sito utilizza cookie, anche di terze parti. Se vuoi saperne di più leggi la nostra Cookie Policy. Scorrendo questa pagina o cliccando qualunque suo elemento acconsenti all’uso dei cookie.I testi seguenti sono di proprietà dei rispettivi autori che ringraziamo per l'opportunità che ci danno di far conoscere gratuitamente a studenti , docenti e agli utenti del web i loro testi per sole finalità illustrative didattiche e scientifiche.

La meccanica ondulatoria di Schroedinger

L'ipotesi di De Broglie fu generalizzata e formalizzata dal fisico austriaco E. Schroedinger, che nel 1926 ottenne un'equazione valida per il moto di una qualsiasi particella in un campo di forza.

L'equazione d’onda di Schroedinger può essere applicata anche ad atomi diversi da quello dell’Idrogeno e risolta (anche se attraverso approssimazioni) con risultati in buon accordo con i dati sperimentali.

Quando si risolve l’equazione d’onda per un atomo particolare si ottiene una funzione, detta funzione d'onda , che presenta come parametri i primi tre numeri quantici, n, l, m.

Una funzione d’onda alla quale vengano attribuiti opportuni valori numerici ai numeri quantici individua lo stato di moto di un particolare elettrone e prende il nome di funzione orbitale.

Ogni funzione orbitale corrisponde ad uno stato stazionario dell’elettrone-onda.

Schroedinger arrivò alla conclusione che l'equazione d'onda che descrive un oscillatore meccanico poteva essere applicata anche all'atomo. Ora in acustica se la frequenza fondamentale è x la frequenza della seconda, terza, quarta......ennesima armonica sarà 2x, 3x, 4x......nx. In altre parole sarà sufficiente un solo parametro ( il numero intero positivo n = 1,2,3..) per individuare qualsiasi armonica.

Nel caso delle onde di Schroedinger il problema è più complesso poichè le onde in questione sono tridimensionali e sono necessari tre parametri per determinare una qualsiasi armonica. Tali parametri saranno anche in questo caso necessariamente quantizzati visto che l'onda in questione è un'onda vincolata e quindi stazionaria.

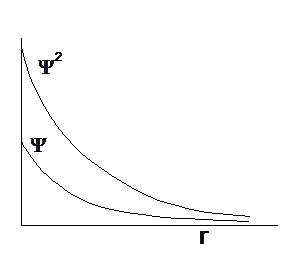
La funzione d’onda Y non ha un significato fisico diretto, mentre il suo quadrato Y2 fornisce la probabilità di trovare l'elettrone nell’unità di volume, comunemente detta densità di probabilità.

Si noti l’analogia con la radiazione elettromagnetica, nel caso in cui si applichino grandezze caratteristiche del modello ondulatorio ad un singolo fotone. In un’onda elettromagnetica l’energia per unità di volume è proporzionale al quadrato dell’ampiezza dell’onda A², dove l’ampiezza è data dall’intensità del campo elettrico o del campo magnetico ad esso concatenato. Se ora passiamo dal continuo al discreto e consideriamo la radiazione come un insieme di fotoni, A² diventa una misura del numero di fotoni presenti nell’unità di volume e, per un singolo fotone, della probabilità di trovarlo nell’unità di volume.

Dati certi valori ai numeri quantici n. l ed m, le soluzioni dell'equazione di Schroedinger non forniscono le coordinate del punto P in cui si dovrebbe trovare l'elettrone rispetto al nucleo posto idealmente all'origine degli assi, ma il valore che in quel punto assume la funzione d'onda Y.

Ciò costringe ad abbandonare il concetto di traiettoria definita e quindi di orbita, per introdurre quello di orbitale, inteso come regione di spazio intorno al nucleo alla quale associare una certa probabilità di trovarvi l'elettrone.

La rappresentazione di un’orbitale può essere fatta in modi diversi. Possiamo vederli esemplificati utilizzando una funzione orbitale particolarmente semplice, quella che descrive l’orbitale s del primo livello energetico (orbitale 1s) nell’atomo di Idrogeno

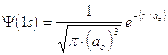
Il modo più diretto di rappresentare un’orbitale è di tracciare la funzione orbitalica Y in dipendenza dal raggio. Nel caso esemplificato si osserva facilmente che per r ® 0 il valore della funzione tende a 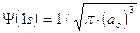¥ la funzione tende a zero. Il suo valore decresce dunque in modo esponenziale man mano che ci allontaniamo dal nucleo. L’orbitale 1s è infinitamente esteso

Y². Infatti nelle regioni dove la nuvola è più concentrata e la densità di punti è maggiore, risulta anche maggiore la probabilità di trovarvi l’elettrone.

Y² ed il volume del guscio stesso.

dP = Y² 4pr²dr

Il rapporto dP/dr rappresenta la variazione della probabilità al variare della distanza dal nucleo ed è quindi una funzione di distribuzione della probabilità in funzione del raggio (radiale)

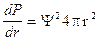
Tale funzione

vale zero in corrispondenza del nucleo (r = 0) in quanto un punto presenta volume nullo
presenta un massimo in corrispondenza di a_o (raggio di Bohr)
si annulla all’infinito (per r ® ¥, r² tende all’infinito, ma Y² tende a zero più rapidamente)

Se sommiamo le probabilità di trovare l’elettrone in ciascun guscio fino ad una certa distanza r, otteniamo la probabilità totale di trovare l’elettrone nel volume compreso tra 0 ed r. (ciò equivale a calcolare l’integrale della funzione da 0 ad r). Tale probabilità complessiva è pari all’area sottesa dalla curva di distribuzione della probabilità. Poiché la funzione si annulla all’infinito, per ottenere una probabilità del 100% è necessario considerare un volume infinitamente grande intorno al nucleo.

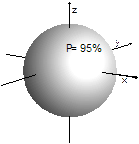
Se tuttavia ci accontentiamo di una probabilità inferiore, ad esempio del 95%, possiamo individuare una superficie tale che la probabilità di trovarvi l’elettrone all’interno sia quella desiderata ed assumere il volume così individuato come rappresentativo dell’orbitale in questione.

Il significato generale dei numeri quantici n, l ed m rimane inalterato anche se è necessario fare le seguenti precisazioni:

Il valore assunto da 'n' determina l'energia dell'orbitale ed individua i 7 livelli energetici possibili, detti anche strati o gusci.
il valore assunto da 'l' è associabile al tipo ed alla forma dell'orbitale. Esistono 4 tipi di orbitali. Gli orbitali 's' presentano simmetria sferica, gli orbitali 'p' presentano una forma a otto di rotazione, gli orbitali 'd' ed 'f' forme complesse.
il valore assunto da 'm' è associabile al numero di orbitali per tipo presenti in ciascun livello energetico.

1 livello 1 orbitale s

2 livello 1 orbitale s, 3 orbitali p

3 livello 1 s, 3 p, 5 d

4 livello 1 s, 3 p, 5 d, 7 f

nei rimanenti 3 livelli (il quinto, il sesto ed il settimo), non si hanno orbitali diversi da quelli già citati.

Naturalmente anche il modello di Schroedinger prevede l'esistenza del quarto numero quantico di spin.

Fonte: http://digidownload.libero.it/quintaachimica/CHIMICA.doc

Autore del testo: non indicato nel documento di origine

Parola chiave google : La meccanica ondulatoria di Schroedinger tipo file : doc

Clicca qui per visitare il portale dedicato alla chimica